Frangi滤波器和模糊C均值算法相结合的织物瑕疵检测

张缓缓, 李仁忠, 景军锋, 李鹏飞, 赵 娟

(1. 西安工程大学 电子信息学院， 陕西 西安 710048;2. 西安理工大学 自动化与信息工程学院， 陕西 西安 710048)



Frangi滤波器和模糊C均值算法相结合的织物瑕疵检测

张缓缓1,2, 李仁忠1, 景军锋1, 李鹏飞1, 赵 娟1

(1. 西安工程大学 电子信息学院， 陕西 西安 710048;2. 西安理工大学 自动化与信息工程学院， 陕西 西安 710048)

为解决织物瑕疵自动检测问题，提出一种基于Frangi滤波器和模糊C均值算法(FCM)相结合的织物瑕疵检测方法。首先采用均值下采样方法对采集的织物图像进行预处理，以减少织物背景纹理信息对织物瑕疵检测产生的影响；然后通过Frangi滤波器滤波增强织物的瑕疵区域；最后利用FCM处理滤波后的图像，确定织物瑕疵区域的像素和非瑕疵区域像素的聚类中心，并分割出瑕疵区域和非瑕疵区域。结果表明，本文方法检测织物瑕疵种类较多，分割效果较好。与其他方法相比，本文提出的算法利用聚类思想对织物疵点进行分割，无需利用正常织物图像进行阈值计算；另外经过滤波后疵点信息明显增强，使得疵点信息与纹理明显不同，从而使聚类更为准确，增加了检测的准确度。

疵点检测； 织物疵点； Frangi滤波器； 模糊C均值聚类算法

织物瑕疵的出现很大程度影响着织物质量和纺织企业的经济效益，因此织物的质量检测在纺织行业中占重要地位。据统计，织物瑕疵对织物销售价格有很大的影响，致使其价格降低45%～65%，严重影响了企业的利润[1]。目前国内许多企业对织物瑕疵检测的方法落后，检测率低且准确度不高[2-3]。此外，织物瑕疵种类繁多、形状各异，这更给准确检测织物的瑕疵提出了挑战。为了适应现代化企业生产的需求，解决传统织物疵点检测方法速度慢，准确率低等缺点, 进一步提高企业的利润，急需开发更先进更智能化的疵点检测方法。

近年来，国内外学者对织物瑕疵检测进行了大量研究。Bu 等[4]采用图像的多重分形特征和支持向量描述数据来检测织物瑕疵。Ngan等[5]选取规则带算法来检测织物瑕疵。Muller等[6]利用2种形态滤波器成功地识别织物的瑕疵，但检测瑕疵种类较少。Mak等[7]利用形态学滤波器对织物处理完成织物的瑕疵检测。Tsai等[8]提出4种不同的瑕疵织物的傅里叶模型，并利用这些模型提取织物瑕疵的傅里叶特征。Kumar 等[9]应用Gabor小波的特性方案，检测平纹和斜纹纹理织物瑕疵。Mak[10]使用多层次可匹配的Gabor函数滤波器检测织物瑕疵。现存的织物瑕疵检测方法可以检测部分织物瑕疵，但检测织物瑕疵的效率和准确度有限，且织物瑕疵种类较多，形态尺寸变化多样；因此，如何高效实时准确检测各种织物瑕疵仍然具有挑战性。本文提出了一种基于Frangi滤波器和模糊C均值(FCM)算法相结合的自动织物瑕疵检测方法，该算法可用于有效地检测不同纹理结构和不同类型的瑕疵。

1 多尺度线性滤波器

在进行织物疵点检测时，如果处理不当，往往会将织物的纹理误报为疵点，这样会对织物瑕疵检测的效率和准确率产生很大的影响，为了有效解决这一问题，首先对采集的织物瑕疵图像进行均值下采样处理，以消除纹理对瑕疵检测的影响。

首先根据织物背景纹理周期大小将图像划分为X×Y的子窗口，织物背景纹理周期根据距离匹配函数计算。然后计算每个窗口中所有像素的灰度均值：

(1)

式中：I(i，j)表示原图像中像素(i,j)的灰度值；X×Y是分块窗口的大小；m=0, 1,…,X；n=0, 1,…,Y。

最后对均值下采样处理后的图像采用双线性插值得到与原始图像同样大小尺寸的图像。

采集的织物瑕疵图像经过均值下采样方法处理后其背景纹理变得平滑，再用多尺度线性(Frangi)滤波器[11]增强织物瑕疵，进而检测分割出织物的瑕疵。

Frangi滤波器是基于 Hessian 矩阵的一种滤波器，它主要被用来提取线性结构的对象，主要通过Hessian 矩阵的各个特征值之间及其对应的线性目标的关系来完成相似性函数的构造，进而提取线性结构。在Frangi提出的方法中对输入图像I，利用其在某点x0处邻域泰勒展开式分析其局部行为：

(2)

式(2)利用最高阶来近似描述图像的结构。其中：▽0,σ是以尺度σ计算的图像的梯度向量；H0,σ是以尺度σ计算的图像Hessian矩阵。在此框架中，微分被认为输入图像与高斯函数微分的卷积：

(3)

其中

(4)

γ用于定义一个规则化的导数族。针对多尺度微分算子，一般情况下，γ设为1。

式(2)中右边第3项的二阶方向导数如下所示：

(5)

通过Hessian矩阵特征向量分析，获得向量的主要方向，使得这些方向上输入图像的局部二阶结构能够被分解。

(6)

(7)

另外，注意到瑕疵具有比背景高的灰度值且其体积仅占整个图像的一小部分，对织物纹理背景像素来说，它的导数值非常小。根据这个特性引入一个测度来区分纹理背景像素，引进的测度S定义如下：

(8)

由于背景像素的对比度低、特征值小致使该测度在瑕疵的背景区域将变得很小。相反，背景像素对比度高，特征值大则测度在瑕疵的背景区域将变得很大。基于上述各分量，Frangi对二维图像的测度函数定义如下：

(9)

织物瑕疵图像经Frangi滤波器处理后，瑕疵区域被增强，如图1所示。

图1 瑕疵区域增强结果图Fig.1 Defect area enhanced. (a) Fabric defect sample; (b) Result obtained by using Frangi filter

2 FCM聚类算法

织物瑕疵图像经过Frangi滤波器滤波后，瑕疵区域被增强，需要进一步将其分割出来。织物纹理图像，不是对瑕疵图像检测所要的信息，需要抑制或者去除；而瑕疵是需要的信息，需要增强或者完全提取出来；针对织物疵点图像可以看作是织物正常纹理信息和疵点信息的叠加，即织物正常纹理是一个类别，瑕疵是一个类别。瑕疵图像经过Frangi滤波器滤液后，瑕疵区域被明显增强，使得织物正常纹理和瑕疵差异加大，从而为FCM聚类算法提供方便。

FCM算法利用耗费函数的迭代优化完成织物瑕疵图像像素的划分[12]。FCM算法的基本思想搜索目标函数迭代的最小化，其定义目标函为

(10)

式中：‖xi-mj‖是xi到mj之间的欧式距离；c是设定的类别数；b是模糊加权指数；xi是第i个像素点的灰度值；mj是第j个聚类中心；M是模糊划分矩阵；V是类中心矩阵；m1,m2,…,mc是c个聚类中心；x1,x2,…,xn是图像n个像素点的灰度值；n是像素点数；μj(xi)是第i个灰度值关于第j类的隶属度值；J(M,V)是织物瑕疵图像的像素到各个聚类中心加权距离的平方和。J(M,V)的值决定图像区域的紧致情况，J(M,V)值越小，则像素灰度值在一个区域的概率就越大，其聚类效果也就越好。在FCM方法中，要满足样本对于各聚类的隶属度的和是1这个条件，即：

(11)

(12)

(13)

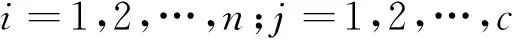
运用FCM算法对织物瑕疵图像的像素进行聚类划分，具体步骤如下：

1)首先设定算法的相关参数，如迭代结束的误差ε、类别数c、模糊加权指数b、最大迭代数tmax、各个聚类中心mi、迭代次数t=1;

2)基于当前的聚类中心利用式(13)计算隶属函数；

3)基于当前隶属函数根据式(12)更新织物图像各个类别的聚类中心；

4)选用适宜的矩阵范数，若‖V(t+1)-V(t)‖≤ε或t≥tmax，结束运算；否则，t=t+1，返回步骤2)。

若FCM算法收敛，可以根据计算得到的不同聚类中心即织物瑕疵聚类中心与非瑕疵背景像素的聚类中心去实现模糊聚类的划分。然后对模糊聚类的结果去模糊化，进而将模糊聚类转变成确定性的分类，从而实现最终瑕疵区域和非瑕疵区域的聚类分割。最后根据织物图像检测结果的白色区域连续像素的多少来判断白色区域是不是瑕疵。

3 实验结果

在织物检测过程中织物纹理信息经常会影响织物瑕疵的检测精度，为了提高检测精度，采用均值下采样方法对采集的图像进行预处理，再用Frangi滤波器对处理后的图像进行处理，增强织物的瑕疵。处理后的图像经过FCM聚类后，图像灰度值被分为正常纹理区域部分与瑕疵区域部分，然后利用分出的类别进行分割。在进行FCM聚类处理时，首先要进行初始化参数。本文采用的织物图像样本主要来源于TILDA织物纹理数据库[13]，样本尺寸是256像素×256像素，Frangi滤波器的尺度范围为[1～10]。检测结果如表1所示，可以看出经过Frangi滤波后，疵点信息显著增强，之后再利用FCM算法对Frangi滤波后图像处理，将疵点区域聚为一类，非疵点区域聚为一类，最后分割出疵点，表中白色是疵点区域，黑色是正常织物区域。提出的算法能很好检测出人眼不易检测的疵点，且检测准确度较高。

表1 部分样本检测实验结果图

Tab.1 Experiment detection result of parts of samples

4 结 论

本文提出了一种基于Frangi滤波器和FCM聚类算法相结合的织物瑕疵检测算法。为了减少背景纹理信息对织物瑕疵检测的影响，选取均值下采样方法对采集的织物图像做预处理，然后通过Frangi滤波器对处理后的图像进行滤波以增强织物的瑕疵区域；最后利用FCM聚类算法对Frangi滤波后的图像进行处理，将瑕疵区域分为一类，非瑕疵区域分为一类，进而分割出织物瑕疵。结果表明，本文方法能有效地检测较多种类织物的瑕疵，分割效果较好，因此具有巨大的应用前景。与其他方法相比，本文算法利用聚类思想对织物疵点进行分割，无需利用正常织物图像进行阈值计算；另外经过Frangi滤波后疵点信息明显增强，使得疵点信息与纹理明显不同，从而使聚类更为准确，增加了检测的准确度。

FZXB

[1] MAK K L, PENG P. Detecting defects in textile fabrics with optimal Gabor filters[J]. International Journal of Computer Science, 2006,1(4): 274-282.

[2] 陈俊杰, 谢春萍. 自动验布系统[J]. 纺织科技进展, 2005(5): 56-57. CHEN Junjie, XIE Chunping. Automatic fabric detection system [J]. Progress in Textile Science & Technology, 2005(5): 56-57.

[3] JING J F, ZHANG H H, LI P F, et al. Fabric defect detection using Gabor filters and defect classification based on LBP and Tamura method [J]. Journal of The Textile Institute, 2013,104(1):18-27.

[4] BU H G, WANG J, HUANG X B. Fabric defect detection based on multiple fractal features and support vector data description [J]. Engineering Applications of Artificial Intelligence, 2009,22 (2): 224-235.

[5] NGAN H Y T, PANG G K H. Regularity analysis for patterned texture inspection[J]. Automation Science and Engineering, 2009, 6(1):131-144.

[6] MUELLER S, NICKOLAY B. Morphological image processing for the recognition of surface defects[J]. SPIE, 1994, 2249: 298-307.

[7] MAK K L, PENG P, YIU K F C. Fabric defect detection using morphological filters[J]. Image and Vision Computing, 2009, 27 :1585-1592.

[8] TSAI I S, HU M C. Automatic inspection of fabric defects using an artificial neural network technique[J]. Textile Research Journal, 1996, 66(7): 474-482.

[9] KUMAR A, PANG G K H. Defect detection in textured materials using Gabor filters[C]//IEEE Trans. 35th IAS Annual Meeting and World Conference on Industrial Applications of Electrical Energy. Rome: Piscataway, IEEE,2000：1041-1047.

[10] MAK K L, PENG P, YIU K F C. Fabric defect detection using multi-level tuned-matched Gabor filters [J]. Journal of Industrial and Management Optimization, 2012, 8(2): 325-341.

[11] FRANGI A F, NIESSEN W J, VINCKEN K L, et al. Multiscale vessel enhancement filtering[C]// Medical Image Computing and Computer-Assisted Interventation-MICCAI’98 Lecture Notes in Computer Science. MA: s.n., 1998: 130-137.

[12] 李旭超，刘海宽，王飞，等. 图像分割中的模糊聚类方法[J]. 中国图像图形学报，2012，17(4):447-458. LI Xuchao, LIU Haikuan, WANG Fei, et al. The survey of fuzzy clustering method for image segment-ation [J]. Journal of Image and Graphics, 2012, 17(4): 447-458.

[13] Workgroup on texture analysis of DFG, TILDA textile texture database[EB/OL]. [2012-10-10]http://lmb.informatik.uni-freiburg.de/research/dfg-texture/tilda.

Fabric defect detection based on Frangi filter and fuzzy C-means algorithm in combination

ZHANG Huanhuan1,2, LI Renzhong1, JING Junfeng1, LI Pengfei1, ZHAO Juan1

(1.SchoolofElectronicandInformation,Xi′anPolytechnicUniversity,Xi′an,Shaanxi710048,China;2.SchoolofAutomationandInformationEngineering,Xi′anUniversityofTechnology,Xi′an,Shaanxi710048,China)

To solve the problem of the various defects generated in the fabric production process, a new method was proposed based on Frangi filter and fuzzy C-means algorithm(FCM) in combination to detect the fabric defects. Firstly, the fabric image sample was preprocessed using mean sampling method to eliminate the influence of background texture on fabric defects. Then Frangi filter was adopted to enhance the fabric defect area. Finally, FCM was used to determine the cluster centers of fabric defective pixels and non-defect region pixel of the Frangi filter image respectively, and defects regional and non-defective regional was segmented. Experimental results show that the proposed method could detect most of fabric defects with better segmentation results.

defect detection; fabric defect; Frangi filter； fuzzy C-means algorithm

10.13475/j.fzxb.20150200205

2015-02-02

2015-05-25

国家自然科学基金资助项目(21301134；61301276)；西安工程大学学科建设经费资助项目(107090811)；中国纺织工业联合会科技指导性项目(2013066);西安工程大学大学生创新创业计划项目(201303012)

张缓缓(1986—)，女，助教，硕士。主要研究方向为图像处理、模式识别。E-mail: zhanghuanhuan0557@163.com。

TP 391

A