传感网中不规则复杂3D平面定位策略研究*

李泽军, 陈 敏†

(1．湖南大学 信息与工程学院,湖南 长沙 410082；2．湖南工学院 计算机科学与信息学院, 湖南 衡阳 421002)

传感网中不规则复杂3D平面定位策略研究*

李泽军1,2, 陈 敏1,2†

(1．湖南大学 信息与工程学院,湖南 长沙 410082；2．湖南工学院 计算机科学与信息学院, 湖南 衡阳 421002)

针对具有障碍物的复杂3D平面定位误差大以及能耗高的问题，如何进行未知节点的定位，提出了一种具有障碍物的不规则复杂3D平面定位策略，该策略将复杂三维平面划分为水平逻辑层并标记节点的所属层，然后在具有障碍物的水平层进行子区域的划分及合并，最后利用大气压传感器测距进行计算未知节点的坐标从而得到3D复杂平面的定位.通过与最新SV定位机制及COLA定位机制在定位误差及能耗进行综合仿真实验对比，本文的定位策略3D-CCD平均定位误差比SV少了5%，比COLA的平均定位误差少8%以上，定位精度上比SV和COLA提高了6.5%以上，及在能耗上比SV和COLA减少了2.7%左右.因此该定位策略(3D-CCD)在解决复杂不规则图形的不确定节点具有较大的优越性.

定位误差；逻辑层；子区域；定位机制

复杂环境下的定位机制大多数都是基于2D网络拓扑环境，导致节点路径估算产生较大的误差以及误差难以控制、传感器节点能耗大等诸多因素.如：ACDL经典方法采用2D定位机制解决复杂网络定位问题，该方法设定一临界点，传感器节点利用邻居节点的通信来判定凹凸表面，并将复杂表面划分为几个子区域，节点通过MDS建立节点的相对位置.最后利用相对位置建立全局2D平面图.这样方法过度临界值的选择，当复杂不平表面无临界值时，该策略将导致失败，另外该定位方法对边界噪音比较敏感.目前，学者们尝试从2D平面扩展到3D平面，其主要采用的定位方法有两种，一是通过将3D复杂平面映射到2D平面来定位其坐标[1,2].二是采用特殊装置来测量凹凸平面的高度值和抛锚节点的距离[3].上述方法对于简单的3D表面定位具有较高的精确度，但对于复杂表面以及具有较大凸高时，其定位误差明显增大和定位不明确.而SV(Single-Value)根据不同节点映射到不同2D平面上且平面的点具有唯一性.然后根据二维平面来定位三维平面.一定程度上解决了较简单的3D平面节点重叠问题[4].但SV的代价较高，对于不规则三维平面也将导致节点重叠现象.COLA定位机制[5]采用移动锚节点来定位三维平面，该方法的精确度较高，但对于复杂3D的平面，由于锚节点的不断移动产生大量的误差值，难以适用大规模3D平面定位.

1 复杂3D平面的分层机制及相关定义

对复杂3D平面进行逻辑水平分层，其分层示意图如图1所示．利用大气压传感器得到节点高度，在得到所有节点的高度后，就可以得到3D平面的最大高度(hh)和最小高度(hl)，若分为L层，当每层的节点数相同时，则可以计算每层的高度为(hh-hl)/l，但在实际情况下，每层的节点数不一致，为保证每层的节点数一致，采用提高层的高度来保证节点数相同并进行标记节点属于哪一层.

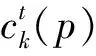
(1)

其中ρ为大于0的常数(通常设为1)，其值为节点跳数与欧氏距离之比例因子.

图1 复杂凹凸平面的水平划分

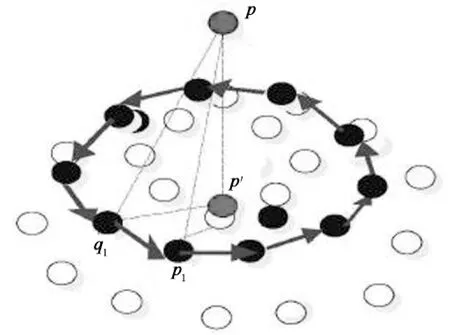
图2 凹凸节点映射关系

2 复杂平面凹凸节点和边界节点的判别

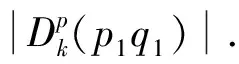
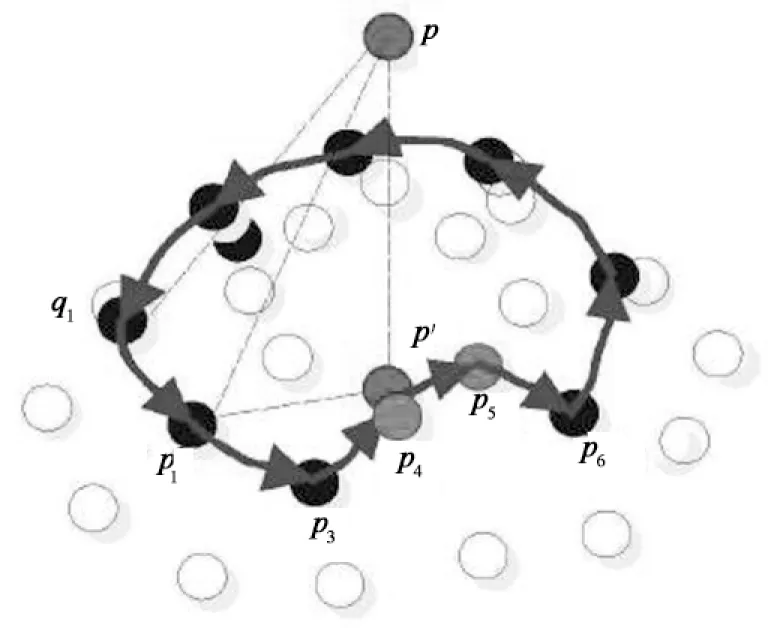
图3 凹凸复杂平面存在障碍物示意图

凹凸节点判别算法描述

输入：设定传感器节点p

输出：凹凸节点判别标识

Step 1 Nodepobtains its neighborsESk(p) withinkhops

Step 5 flagconver←true

Step 6 else

Step 7 flagconver←false

Step 8 endif

3 凹/凸层的分解

为减少算法的迭代次数以及算法的开销，通过节点凹/凸度将纵深区域分解成多个子区域层.依据凹凸节点算法可以将分层后的凹凸节点度计算出来，这里分层的依据是最大凹凸度的节点.下面详细阐述其分解凹凸层的方法.

3.1 以凹凸节点度构建子区域

由于子区域中可能存在障碍物记为hole，因此分为2种情况：

2)当子区域存在障碍物时，图4表示存在多个障碍物，这里以2个障碍物为例进行说明.S={s1,s2,s3,s4,s5}，锚节点为s1,s5.

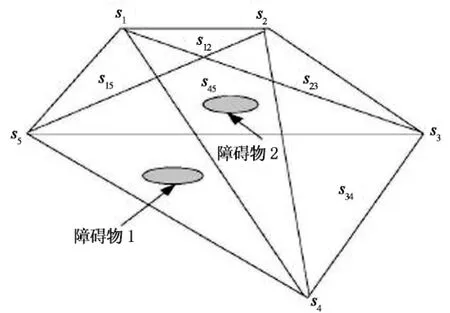
图4 区域平面存在障碍物

计算区域存在hole1和hole2两个障碍物的最短路径时，由于锚节点为s1,s5会形成完全图G，将图G划分为若干个子区域，则障碍物只可能存在于子区域内.为减少障碍物对定位精度的影响，这里采用避障方式进行处理．其处理步骤如下．

步骤1：计算并标记锚节点之间所有节点的最短路径，其标记方法为如节点s2,s5记为PS2S3.

步骤2：含有障碍物的边界节点发送广播以确定最近节点的最短路径.

步骤3：障碍物坐标可依据锚节点坐标和步骤2进行计算，如图4中，通过步骤1和步骤2分别标记和确定3条最短路径(即s1s4,s3s5及s4s5)并计算路径交点s4，s5，s45，这样就能得出障碍物1(hole1)属于s4s5s45子区域.同理可计算其余障碍物的归属.

步骤4：依据障碍物位置及障碍物归属的子区域，若hole⊂Δsisjsk，则规定约束条件si,sj,sk不能同属于一个子区域.根据此约束条件遍历所有子区域锚节点.若锚节点不属于同一子区域，将锚节点加入禁忌队列中.在锚节点遍历中，为减少算法复杂度，优先采用最短路径算法.

步骤5：依据步骤1和4对3D复杂平面进行子区域划分.

3.2 确立新根节点子区域

3.3 合并子区域及构建层区域

在进行子区域的建立时采用广播的方式进行信息传递，导致在层区域内形成若干个子区域并且子区域可能产生重叠现象.若节点p接收多个构建子区域信息时，以第一时间收到的信息作为标记加入到该子区域中，其余消息将被丢弃.否则若子区域标记不相同则合并两个子区域直到合并消息不存在.

复杂凹凸平面的分解与子区域的合并算法描述如下：

Algorithm:convex/concave decomposition

Input:Set of convex/concave node degree

Output: Set of convex/concave sub-regions

Step 1:Set SID=NULL

Step 2:for each sensor nodes pi

Step 3:if then

Step 4:Choose pi as RootNode

Step 5:end if

Step 6:end for

Step 7:if no such node exits then

Step 8:Choose the node p(closest to the middle floor) as RootNode

Step 9: end if

Step 10: if and exits Hole

Step 11:for each anchor sensor Si in region S

Step 12: for each anchor sensor Sj in region S

Step 13:shortest path

Step 14:end for

Step 15:end for

Step 16: for each sensor pi

Step 17: mark pi=smsn

Step 18:end for

Step 19: for each boundary sensor bi of Hole

Step 20: bi sends Message _in

Step 21:mark the nearest node pi and the shortest

Step 22: end for

Step 23:if exits , , then

Step 24:hole

Step 25:add sa,sb,sc to prohibition queue

Step 26:end if

Step 27:end if

Step 28:for each sensor nodes Pi

Step 29:if then

Step 30:RootNode sent Message _in to pi

Step 31:if pi:SID=NULL and pi prohibition_quenu then

Step 32:set pi:SID=Message_in

Step 33:else Merge the two sub-regions

Step 34:end if

Step 35:else choose pi as new RootNode

Step 36:end for

4 复杂平面定位与计算

在复杂3D平面定位计算中主要考虑模型构建差生的误差以及定位方法和过程.传感器节点在进行通信时其物理层的传播模式可以任意，其公式为[7,8]：

(2)

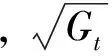
由于3D平面的模型比较复杂，这里采用地形平面误差[9](terrain plane error)记为TPE进行修正，其公式如下：

(3)

式中zi,zei分别为传感器节点p实际坐标与测量值坐标.为减少人为测距对模型的影响，这里采用误差修正模型抑制.其修正模型如下：

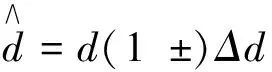
(4)

Δq=k1e+k2．

(5)

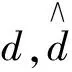
通过第三节分层子区域后，利用三角形三边进行传感器节点定位，如可根据锚节点p1，p2，p3来定位节点i.h1表示节点i的高度，hp1,hp2,hp3分别为三个锚节点高度，其与i的斜线距离用x1,x2,x3表示.则映射到平面的距离用r1,r2,r3表示，可以通过以下计算r1,r2,r3.

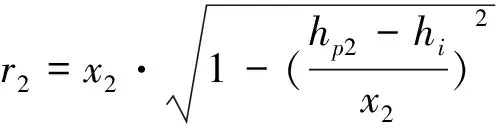
(6)

由公式(6)可以转化公式为：

通过求解方程组可得到：

2x(x2-x1)+2y(y2-y1)=D1,2；

2x(x3-x1)+2y(y3-y1)=D1,3．

(8)

则未知节点i坐标(x,y)的计算公式如下：

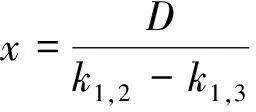
(9)

(10)

公式(9)和(10)中的D以及p1,2和p1，3的计算如下：

(11)

(12)

(13)

以上公式的计算可以得出未知节点的坐标，遍历所有子区域内的节点，得到整个复杂平面全局地图.

5 实验参数设置及算法性能评估

试验中网络3D复杂平面区域为1 000 m×1 000 m×500 m，采用Matlab进行仿真，这里假设网络为连通的，节点高度通过气压传感器进行测量其高度.传感器节点数分别采用1 000,2 000,4 000并且随机散播在整个复杂网络.通信半径为100，节点跳数设为k=3，传感器节点间欧式距离与节点跳数比例因子δ=0.4.

定位率：定位节点与整个节点之间的比值.

定位误差：传感器节点实际坐标用(x,y,z)表示,估测坐标用(xe,ye,ze)表示，传感器节点通信半径用R表示，相邻节点距离用l表示，节点间实际距离用l′表示.则定位误差和平均定位误差可用以下公式进行计算[10]：

(14)

(15)

信号强度：信号强度采用传统信号强度公式计算：

pd=po-10×2×log10(f)-10×2×log10(d)+27.56

(16)

在实验中通过将凹凸复杂平面定位策略研究(Concave-convexcomplexplatdemonstration记为3D-CCD)与目前最新流行算法SV,COLA在定位率、平均定位误差以及计算开销方面进行对比，以此来评价各算法的综合性能.

从上述图5,图6和图7可以看出:随着测量距离的增大，各算法的定位率都有不同程度的下降，COLA下降的尤为明显，而本文算法依然表现出较高的定位率.这是由于复杂3D平面具有障碍物的原因，导致分割的子区域更多的缘故.下面进行平均误差的仿真.

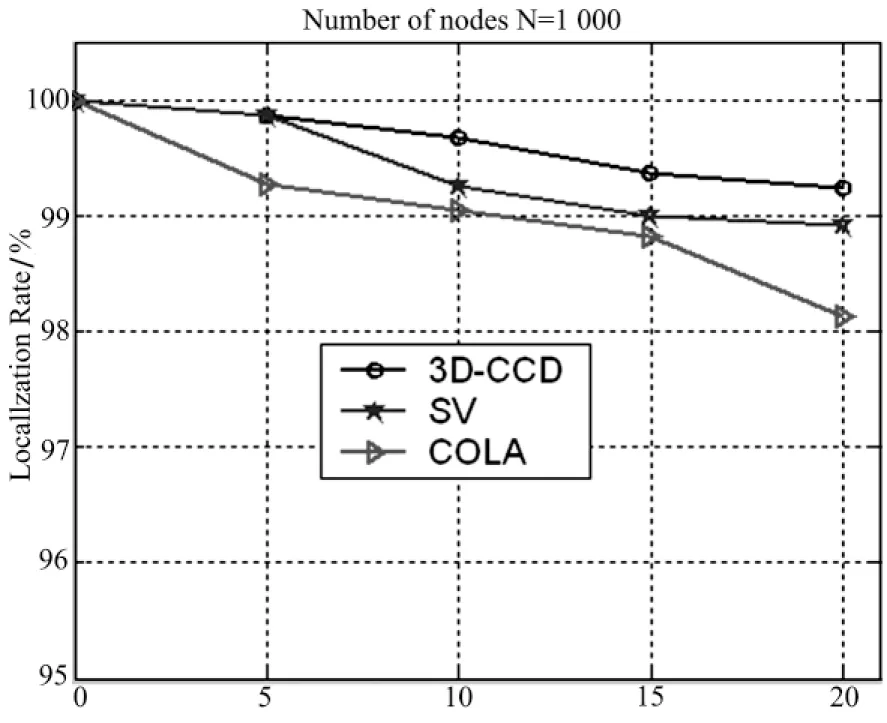
Measurement Error/%

Measurement Error/%

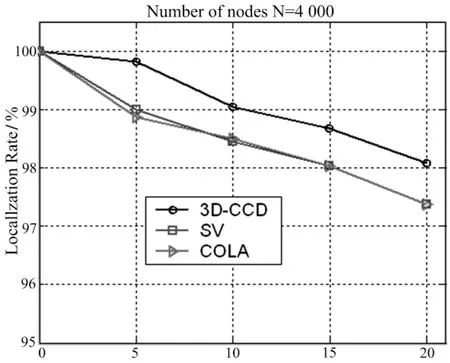
Measurement Error/%

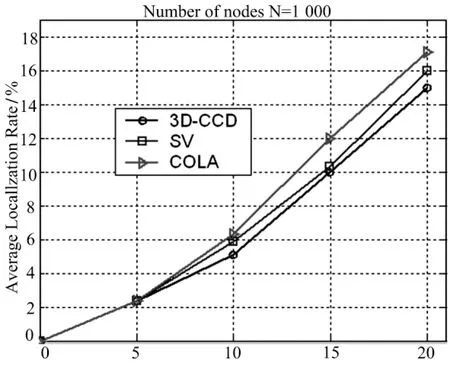
Measurement Error/%

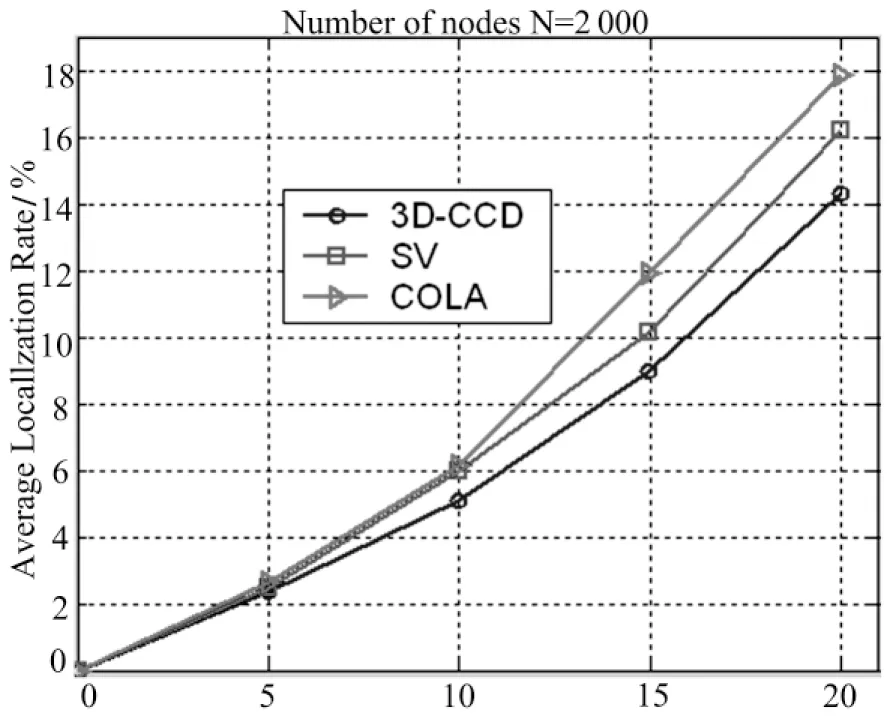
Measurement Error/%

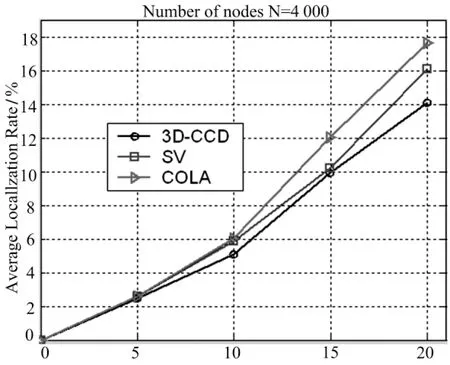
Measurement Error/%

从图8～10中的实验数据可以得出：当测量距离增大也即测量误差增大时，三种算法的定位精度都有所下降，并且三种算法算法的平均误差都所有增加．但与SV及COLA算法对比，本文算法3D-CCD的平均误差在节点数为1 000时比SV要低6.8%，比COLA算法要低13.6%，而在节点数增加到4 000时平均误差比SV要低7.2%，比COLA算法要低14.7%.这是因为3D-CCD采用凹凸分层策略以及子区域合并策略来避免障碍物的原因.说明本文算法3D-CCD能准确定位未知传感器节点坐标并且误差与网络模式无关.下面进行算法的开销仿真.

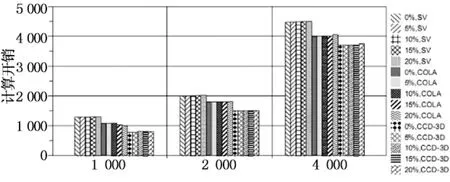
节点数

图11表示3D-CCD算法的开销在不同测量误差时都要比SV及COLA算法的开销要小，这是由于3D-CCD采用的迭代次数少的缘故.

6 结束语

本文研究复杂3D平面的定位机制，该策略首先将复杂三维平面进行逻辑水平分层，然后在水平层进行子区域的划分及合并处理，最后用大气压传感器测距进行计算未知节点的坐标从而得到3D复杂平面的定位.该思路为不规则复杂三维平面提供了新的思路.该策略尤其适用于不确定节点的定位.

[1]ZHAOY,WUH,JINM,etal.Localization in 3D surface sensor networks: Challenges and solutions[C]//The 31st Annual IEEE International Conference on Computer Communications (IEEE INFOCOM 2012)．Orlando, Florida,USA,2012:55-63.

[2] LIU Q,REN P,ZHOU Z. Three-dimensional accurate positioning algorithm based on wireless sensor networks[J].Journal of Computers, 2011, 6(12): 2582-2589.

[3] LIU C,JIANG H,ZENG L D.Unitary matrix pencil algorithm for range-based 3d localization of wireless sensor network nodes[J]. Journal of Networks, 2012, 7(9):1384-1390.

[4] 赵德鑫,李婷,黄芝平,等.无人潜航器舷侧阵声呐匹配场被动定位方法研究[J].湖南大学学报：自然科学版,2013,40(8):76-82.

ZHAO De-xin,LI Ting,HUANG Zhi-ping,etal.Matched-field source localization using the flank array of unmanned under water vehicle[J].Journal of Hunan University:Natural Sciences, 2013,40(8):76-82. (In Chinese)

[5] STOLERU R,HE T,MATHIHARAN S S,etal.Asymmetric event-driven node localization in wireless sensor networks[J]. Parallel and Distributed Systems, IEEE Transactions on, 2012,23(4): 634-642.

[6] 杨高波,吴潇,张兆扬,等.基于过渡像素的视频图像文本检测与定位[J]． 湖南大学学报:自然科学版,2011,38(6):69-74.

YANG Gao-bo,WU Xiao,ZHANG Zhao-yang,etal.A transition pixels based text detection and localization for video images[J]. Journal of Hunan University:Natural Sciences, 2011,38(6):69-74.(In Chinese)

[7] CUI H,WANG Y.Four-mobile-beacon assisted localization in three-dimensional wireless sensor networks[J]. Computers & Electrical Engineering, 2012, 38(3): 652-661.

[8] WANG R J,QIN Z G.A weighted 3D localization algorithm based on partial hopsize in wireless sensor network[J]. International Journal of Advancementsin Computing Technology,2012, 4(9): 504-513.

[9] WANG Y,LIU Y,GUO Z.Three-dimensional ocean sensor networks: A survey[J]. Journal of Ocean University of China, 2012, 11(4): 436-450.

[10]王小平,罗军,沈昌祥.无线传感器网络定位理论和算法[J].计算机研究与发展, 2011,48(3):353-363.

WANG Xiao-ping,LUO Jun,SHEN Chang-xiang. Theory and algorith mson localization in wireless sensor networks[J]. Journal of Computer Research and Development, 2011,48(3):353-363. (In Chinese)

The Study of Positioning Strategy of Irregular 3D Plane in Sensor Networks

LI Ze-jun1,2, CHEN Min1,2†

(1.College of Information Science and Engineering, Hunan Univ,Changsha, Hunan 410082, China;2.School of Computer and Information Science,Hunan Institute of Technology,Hengyang , Hunan 412002,China)

Considering the large positioning error and high energy consumption concerning irregular and complex 3D plane with obstacles, this paper put forward a new strategy to locate the unknown nodes. This policy divides the complex three-dimensional plane into different logic layers and labels each layer node it belongs to. Then, sub-regions are divided and merged in horizontal layers. Finally, the positioning of 3D complex plane is possible by calculating the location coordinate of unknown nodes after atmospheric pressure sensor ranging. Compared with SV and COLA, the 3D-CCD positioning strategy in the average positioning error is 5% less than SV and 8% less than COLA． Its positioning precision increases more than 6.5%， and the energy consumption reduces 2.7% than SV and COLA. The 3D-CCD has great advantages in terms of positioning error, accuracy and energy.

positioning error；logic layer；subdomain ；positioning mechanism

1674-2974(2015)08-0125-07

2014-10-12

国家自然科学基金资助项目(61472127) ，National Natural Science Foundation of China(61472127) ;湖南省自然科学基金资助项目 (13JJ9026)

李泽军(1972-)，男,湖南常宁人，湖南大学博士生

†通讯联系人，E-mail:9918428@qq.com

TP39

A