基于两相流沸腾传热模型的缸盖温度场辨析*

杨 靖，张思远，刘凯敏，王 毅，郭华礼，孙 承，李 克

(1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082;2.湖南大学 先进动力总成技术研究中心，湖南 长沙 410082)

基于两相流沸腾传热模型的缸盖温度场辨析*

杨 靖1,2†，张思远1,2，刘凯敏1,2，王 毅1,2，郭华礼1,2，孙 承1,2，李 克1,2

(1.湖南大学 汽车车身先进设计制造国家重点实验室，湖南 长沙 410082;2.湖南大学 先进动力总成技术研究中心，湖南 长沙 410082)

为了更精确地研究发动机缸盖温度场的分布，在Eular多相流模型的基础上，结合Rohsenow核态沸腾传热模型，建立新的可用于内燃机缸盖水腔内过冷沸腾数值模拟的两相流模型.以某汽油机缸盖为研究对象，分别采用BDL和Rohsenow两种传热模型，利用CFD技术对其进行流固耦合传热计算和分析.结果表明，采用Rohsenow沸腾传热模型能够比BDL沸腾模型更精确地计算缸盖温度场；缸盖的最高温度192.22 ℃，最大应力156 MPa，均满足缸盖材料的强度条件.

缸盖；温度场；两相流；沸腾传热

气缸盖是发动机最核心、最复杂的工作零件之一，缸盖的燃烧室是发动机点火和燃烧的最重要场所．高温气体通过缸盖下表面将大量热量传递给缸盖内的冷却水，缸盖鼻梁区和气门座圈等位置成为缸盖上温度最高、热应力最大的部位[1].由于发动机缸盖恶劣的工作条件，其质量和使用寿命在很大程度上受到冷却系统的制约.研究表明，高压缩比、高增压、小排量技术将成为当今世界发动机技术的发展方向，发动机强化程度将会越来越高[2].发动机功率的提升必然会面临高强度下的热负荷问题.因此发动机缸盖的高温冷却技术成为研究冷却系统的重点.

近年来，由于实验研究的昂贵成本和计算机技术的不断发展，流固耦合传热仿真方法越来越普遍地被应用于实际发动机的开发过程[3].常用的发动机冷却水传热计算模型有Chen模型和BDL模型[4].BDL模型是从Chen模型改进而来的，考虑了局部流动参数和饱和状态对沸腾传热的影响，更加适用于局部流动传热计算[5].白曙[6]将Chen和BDL两种模型进行了计算和试验对比，表明后者的计算精度更高.董非等[7]将BDL模型进行了修正，提高了过冷流动沸腾传热的精度，但属于单相对流传热，没有考虑相变的影响.刘永等[8]利用编程也开发出一种沸腾传热模型，但亦属于单相对流传热，并且计算过程比较复杂，不易实现.

本文在Euler多相流模型的基础上将Rohsenow核态沸腾换热准则方程应用于沸腾换热的两相热流传递，对比分析了两相流沸腾传热与BDL单相沸腾传热的计算精度.然后以某高速四缸汽油机气缸盖为研究对象，以该沸腾传热模型为基础，对其进行了考虑沸腾传热的流固耦合计算，得到了缸盖的温度场和应力场分布，并分析了两相沸腾传热对缸盖冷却的影响和气缸盖鼻梁区的气泡堵塞状况.

1 传热模型的数学描述

1.1 两相流基本方程

两相流模型可分为均相模型和分相模型两种.均相模型是把两相介质看做均匀介质，介质的参数取两相平均参数，然后再根据单相均匀介质建立两相流基本方程；分相模型则是把两相分成两种单相流动，即气相和液相，介质的参数分别取各自的介质参数进行运算.为了提高模拟的精度，本文采用分相模型来解释两相流的基本流动过程.

数学描述的公式如下[9]：

连续性方程：

液相连续性方程：

(1)

气相连续性方程：

(2)

式中：dWl为液相界面效应；Cl为其周界.dWg为气相界面效应，而且dWG=-dWl=q/λ；λ为潜热(kJ/kg)；q为热流密度(kW/m2)．

液相动量方程

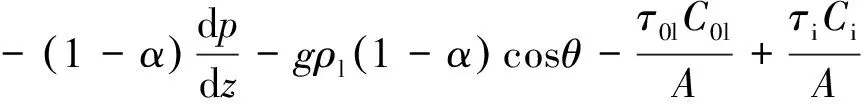
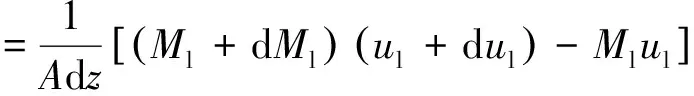
(3)

气相动量方程

(4)

式中：C0g，C0l分别为气相、液相所接触的流道壁面周界，且C0g+C0l=C0，C0为流道壁面总周界，Ci为界面周界.

分相模型两相流能量方程：

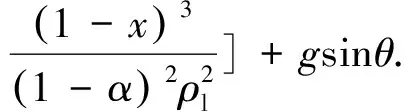
(5)

1.2 传热控制方程

Rohsenow认为热流密度的增加是由于脱离泡沫尾流后面的液体流动增强了搅动的缘故，提出了将湍流对流换热的基本准则扩展用于核态沸腾换热的准则方程，拟合数据后得到了一个适用性很广的描述热流密度的综合关系式，用于计算沸腾表面热流量[10]，

(6)

式中：μl，Cpl，ρl和Prl分别为液体的动力粘度，比热容，密度和普朗特数；np为普朗特数的指数，一般为1.73；g为重力加速度；ρv为气体密度；σ为气液交界面的表面张力系数；Tw为壁面温度；Cqw为随着液体表面变化的经验系数.

在发生沸腾区域，气泡开始生成后逐渐增多直到充分发展气泡沸腾点FDB(fullydevelopedboiling)，气泡不断地生成然后破裂，蒸发与冷却凝结处于平衡状态，于是产生气泡的那部分热流密度qB可用如下传热关系与凝结传热关联[9]：

(7)

htr,l为单相液对流传热系数，它与凝结传热系数htr,c成比例关系；B0为比例系数；Ac/A为单位受热面积的气液界面面积.

过冷沸腾起始点ONB(onsetofthenucleateboiling)与FDB之间的空泡率方程：

(8)

其中，αFDB=aCh/F,

Bl=1.07；Ch为流道周界；F为流通截面积.

1.3 流固耦合控制方程

流固耦合传热计算的关键是流体与固体交界面的热量传递.由能量守恒可知，在流固耦合界面处，固体传出的热量应等于流体吸收的热量.为此，采用下面方程描述能量守恒，建立固体的Fourier 热传导方程和流体的对流换热控制方程之间的联系[11]：

(9)

式中：Kcond为固体导热系数；qconv为热交换量；hconv为局部对流换热系数；Tf为流体温度；Tw为壁面温度.

固体侧假设为常物性稳态导热问题，并认为固体无内热源，则其导热微分[12]方程为：

(10)

式中：x,y,z为坐标分量；t为温度.

流体侧采用k-ε湍流模型计算流体与壁面的对流传热边界条件，固体传热边界则综合采用第1和第3类边界条件.

2 试验与计算

2．1 试验模型

英国的Robinson博士曾经在一个冷却水道装置中进行过沸腾试验[13]．为了验证本文提出的沸腾模型应用于过冷流动沸腾传热的计算精度，在此引用了这次试验的结果.

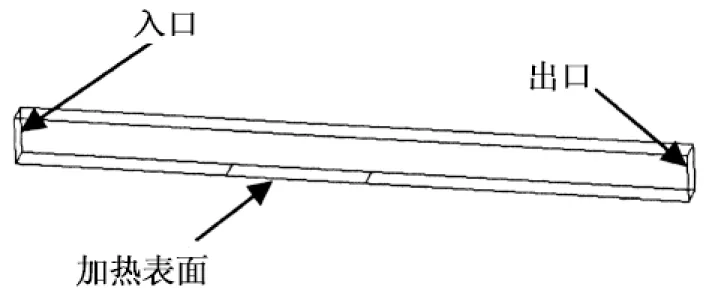
图1 试验冷却水道示意图

该试验装置如图1所示，管道长度为241mm，截面尺寸为16mm×10mm，加热壁面尺寸为50mm×10mm，距离入口76mm.工质为纯水与乙二醇的混合物.采用两组工况的试验数据，工质的工作压力为0.1MPa，两组试验的入口速度分别为0.25m/s和1m/s，温度均为363K.每组工况中，保持进口速度和温度不变，只改变加热面的温度，得到了两组热流密度随壁面过热度的变化而变化的数据.两种试验工况下的边界条件如表1所示.

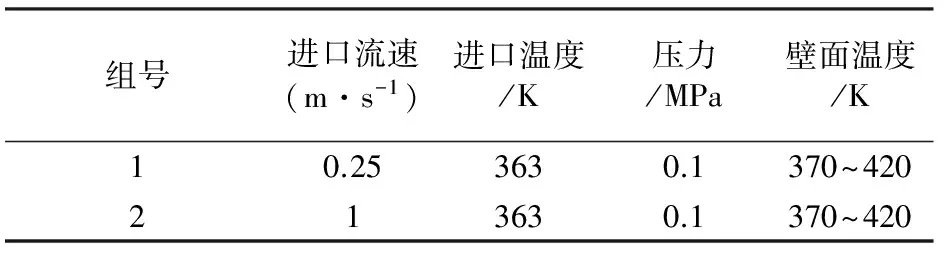
表1 边界条件

2．2 计算结果与分析

对试验冷却水道进行数值模拟时，计算模型按实际物理模型构造，数学模型分别采用本文提出的两相流沸腾模型和BDL沸腾模型.出入口的边界条件按照试验设置的数值给定.图2给出了流体流速分别为0.25 m/s和1 m/s时热流密度的试验值和CFD计算值的对比，计算模型中工质的边界设置均相同.由于试验的误差和数值模拟中边界条件的理想化，计算结果和试验数据一定存在误差，但此处旨

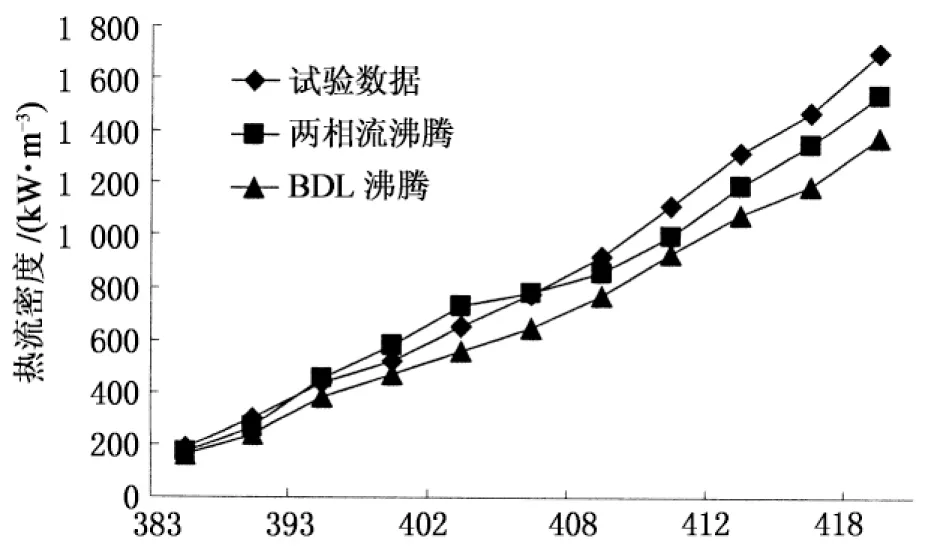
壁面温度/K(a) 流速0.25 m/s，压力0.1 MPa

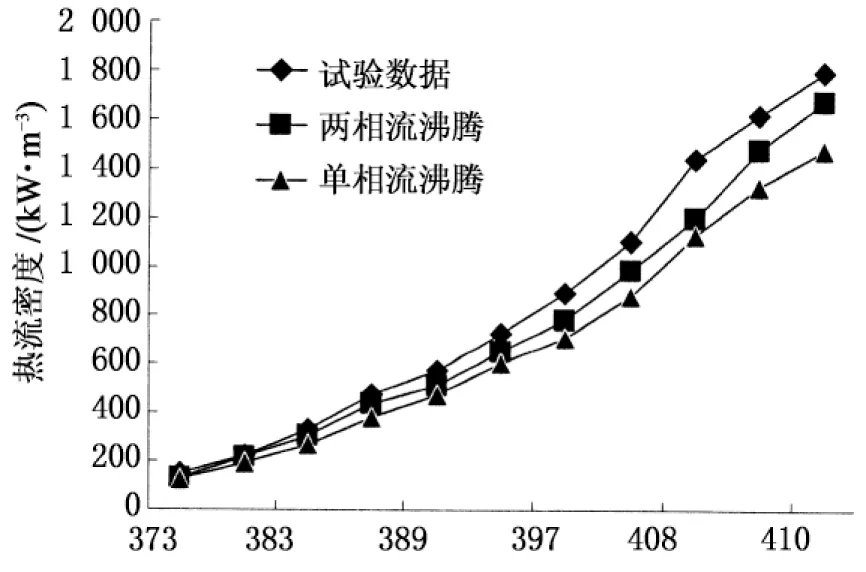
壁面温度/K(b) 流速1 m/s，压力0.1 MPa

在对比新的沸腾换热模型和BDL沸腾换热之间的差别，两组计算数据除了传热模型不同外，其他边界均相同，因此具有可比性.图中可以看出，考虑了新的沸腾模型后得到的数据与实验值之间的误差均比考虑BDL沸腾模型的误差小，后者比前者的误差大将近10%，而应用了该沸腾模型后的误差平均值为9.3%，因此该模型具有实际应用价值.

3 工程实例应用

本文以某四缸高速汽油机气缸盖为研究对象，分别运用本文提出的Rohsenow两相沸腾模型与BDL沸腾模型进行流固耦合计算，对比结果并分析缸盖冷却状况.

3．1 网格划分与材料属性

缸盖网格模型如图3所示.计算时缸盖网格为911 581个体网格.材料为铝合金ZL101A，密度为2.68×103kg/m3，弹性模量47 000 MPa，泊松比为0.3，其他材料属性参照金属材料手册.

图3 缸盖实体网格

3．2 缸盖温度场边界

发动机工作过程中最主要的热量来源就是缸内燃烧，缸内温度场描述的准确度对缸盖的传热模拟精度至关重要.本文在对发动机进行三维建模后利用专业的内燃机CFD软件模拟缸内燃烧过程.图4为发动机工作一个循环周期内燃烧室火力面、进排气门座圈和进排气道的最高温度场和换热系数分布(限于篇幅，进排气道未列出)，最后将计算结果映射到缸盖模型中作为缸盖流固耦合的热边界.

(a) 进气门座圈

(b) 排气门座圈

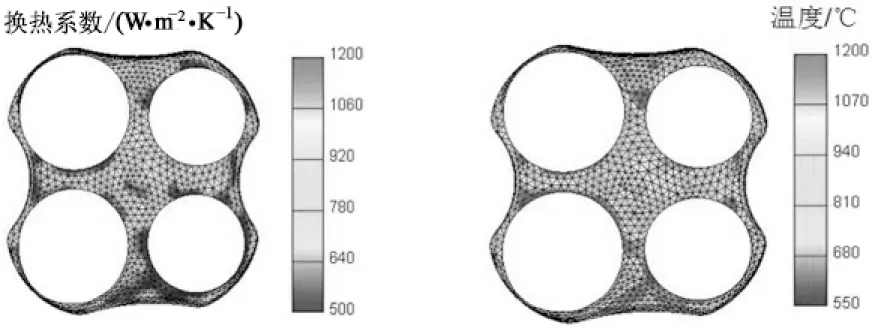
(c) 火力面

3．3 缸盖水套流动边界

该发动机水套内的冷却水经过水泵后进入缸体，由气缸垫孔向上流入气缸盖水套，然后一部分冷却水从节温器流进散热器，另一部分从缸盖水套流入排气歧管和排气总管，继而进入散热器.如图5所示，作为缸盖水套入口的气缸垫孔共有26个，因而气缸盖水套的各孔流量不同，为得到各孔具体的流量值，需要首先计算发动机整机冷却系统的流动状态.利用CFD软件模拟这一过程，模型如图6所示.该计算网格以多面体为主，为了保证缸盖上水孔等重点部位的网格质量和边界层要求，网格尺寸较小，总数超过300万.通过台架试验测得的边界条件为：入口质量流量3.91 kg/s，节温器处出口压力0.1 MPa.计算得到缸垫上水孔流量(如图7所示)和排气歧管流向缸盖的冷却水流量.

图5 缸垫孔的编号

图6 整机流场网格划分

上水孔编号

3．4 缸盖温度计算

3.4.1 温度场计算与实验对比

为了验证两相流沸腾传热模型在缸盖冷却中的应用效果，对发动机缸盖表面温度进行了试验测量.由于水套的影响，只在缸盖两端进行了打孔放置温度传感器，传感器位置如图8所示.

图8 缸盖温度测点布置

表2为测点试验温度值与计算值的对比.从表2中对比分析知，采用本文提出的两相流沸腾模型后，两个测点的计算值与试验值之间的误差均比原BDL沸腾模型下的误差小.1缸测点误差最小，仅为3.08 %，4缸误差稍大，为5.19 %.而BDL沸腾传热模型下，4缸测点误差最大，达到11.8 %，1缸误差稍小，为7.69 %.相比之下，采用新的两相流沸腾模型后，1缸的计算误差比BDL沸腾模型减小了60 %，而4缸测点的误差减小了56 %.前者考虑了相变对传热过程的影响是精度提高的主要原因.新的两相流沸腾传热模型适用于发动机缸盖的传热计算.

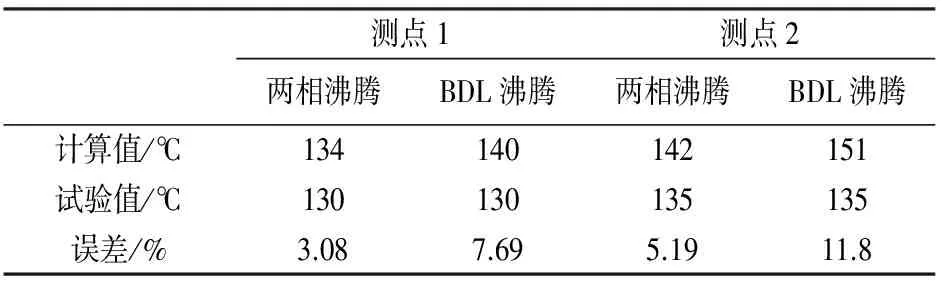
表2 缸盖测点温度计算值与试验值对比

3.4.2 计算结果分析

缸盖水套内流体的温度场分布如图9所示，从中可以看到水套内最高温度为138.59 ℃，出现在第3缸和第4缸的鼻梁区.这些区域冷却水温度都已达到饱和温度，说明发生了沸腾现象.从图5和图7可看出，位于第3缸和第4缸排气侧的9，10，12，13，14号缸垫孔流量较小，导致了该区域的温度较高.而1缸和2缸有排气歧管侧的大量冷却水补充，温度较低.图10为水腔内空泡率的分布图，第3，4缸鼻梁区出现明显的沸腾气化现象，空泡率最大值达到94%，且大部分加热面均在60%以上.从第三缸的中心切面图可以清楚看到过高的气化只出现在鼻梁区的壁面处，由于鼻梁区主流冷却液的温度低于对应压力下的饱和温度，沸腾产生的气泡在脱离加热壁面后，在低温主流流体中迅速冷凝破灭，不会对鼻梁区的狭小水流通道造成堵塞现象.

图9 缸盖冷却水温度场

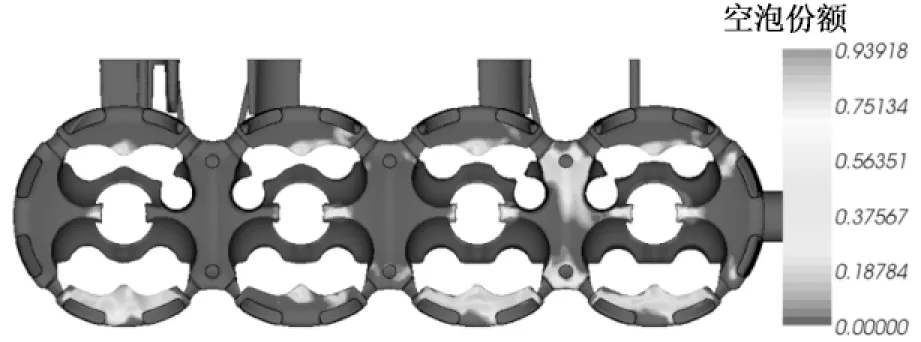
(a) 水套内空泡率

(b) 空泡率大于0.1的区域

图11为气缸盖整体温度分布，从第1缸到第4缸温度逐渐升高，最高温度为192.22 ℃，出现在第三缸和第四缸的火花塞和排气管组成的鼻梁区.由相关文献可知，铸造铝合金要求的工作温度≤260 ℃[14]，本机的缸盖温度符合其要求.图12给出了缸盖在该温度场分布下的热应力分布，从图中可看出缸盖大部分区域热应力均在60 MPa以下.最高热应力出现在火花塞附近进气道与排气道之间，鼻梁区应力可达156 MPa.缸盖材料为铝合金，其屈服极限为235 MPa[15]，从计算结果看，该缸盖的热应力满足材料的强度条件.

图11 缸盖温度场

图12 缸盖应力分布

4 结 论

1)本文以Eular多相流理论为基础，结合Rohsenow核态沸腾换热准则方程建立了两相流沸腾传热模型，并用试验数据验证了该传热模型计算结果的正确性.结果表明，在直管沸腾中，该模型的计算精度较BDL沸腾模型提高了10%.

2)对比燃烧室火力面测点温度的试验数据，在缸盖流固耦合传热模拟计算中，运用三维流体计算、缸内燃烧计算、换热系数计算等模拟结果，通过映射的方法使两相流沸腾传热温度场计算更接近于实际，计算结果较试验结果误差仅为3.08%，比BDL模型计算误差减小60%.

3)冷却计算结果可用于评价缸盖结构设计及冷却效果情况.本文所研究的缸盖温度最高为192.22 ℃，安全系数为1.35；热应力最大156 MPa，安全系数为1.5，满足缸盖材料要求.火力面小部分区域发生了沸腾传热现象，但气泡很快破灭，没有对流动造成堵塞.

[1] 许道延，丁贤华．高速柴油机概念设计与实践[M]．北京：机械工业出版社，2004：59-60．

XU Dao-yan，DING Xian-hua．Design and practice of the concept of high speed diesel engine[M]．Beijing：China Machine Press，2004：59-60．(In Chinese)

[2] HEYWOOD J B, WELLING O Z. Trends in performance characteristics of modern automobile SI and diesel engines[J]．SAE International Journal of Engines, 2009,2(1):1650-1662.

[3] 刘国庆，舒歌群，张志福，等．考虑沸腾换热的内燃机流固耦合传热分析[J].内燃机学报，2011，29(6)：543-548．

LIU Guo-qing，SHU Ge-qun，ZHANG Zhi-fu，etal．Analysis of fluid solid coupling heat transfer in internal combustion engine considering boiling effect[J].Transactions of CSICE，2011，29(6)：543-548．(In Chinese)

[4] 麦华志，李国祥．缸盖冷却水的单相流沸腾模型[J]．山东内燃机，2005(2)：8-11．

MAI Hua-zhi，LI Guo-xiang．Single-phase boiling flow models of cylinder head coolant flow[J]．Shandong ICE，2005(2)：8-11．(In Chinese)

[5] ABLINGER S．Alibrierung und verifikation von siedemodellen fur die 3Dstromungssimulation[D]. Diplomarbeit an der TUGraz，2002．

[6] 白曙．适用于缸盖冷却系统的沸腾模型研究[J]．柴油机设计与制造，2011，17(4)：169-173．

BAI Shu．Research on boiling model for cylinder head cooling system[J]．Design & Manufacture of Diesel Engine，2011，17(4)：169-173．(In Chinese)

[7] 董非，郭晨海，范秦寅，等．发动机冷却水腔内沸腾传热的模拟研究[J]．内燃机工程，2011，32(4)：76-82．

DONG Fei，GUO Chen-hai，FAN Qin-yin，etal．Simulation on boiling heat transfer in cooling water jacket of engine[J]．Chinese Internal Combustion Engine Engineering，2011，32(4)：76-82．(In Chinese)

[8] 刘永，李国祥，付松，等． 一种适用于缸盖水腔沸腾传热计算的模型[J]．内燃机学报，2008，26(1)：76-82．

LIU Yong，LI Guo-xiang，FU Song，etal．A new single phase boiling model for heat transfer calculation of cooling water-jacket in cylinder Head[J]．Transactions of CSICE，2008，26(1)：76-82．(In Chinese)

[9] 鲁钟琪．两相流与沸腾传热[M]．北京：清华大学出版社，2002：201．

LU Zhong-qi．Two-phase flow and boiling heat transfer[M]. Beijing： Tsinghua University Press，2002：201．(In Chinese)

[10]ROHSENOW W M． A method of correlating heat transfer data for surface boiling of liquids[R]. Cambridge: Division of Industrial Cooperation，MIT,1951．

[11]骆清国，刘红彬，龚正波，等．柴油机气缸盖流固耦合传热分析研究[J].兵工学报，2008，29(7) ： 769-773．

LUO Qing-guo，LIU Hong-bin，GONG Zheng-bo，etal. Study on the fluid-solid coupled heat transfer of the diesel engine cylinder head[J].Acta Armamentarii，2008，29(7)：769-773．(In Chinese)

[12]邓元望，袁茂强，刘长青．传热学[M]．北京：中国水利水电出版社，2010：19-21．

DENG Yuan-wang，YUAN Mao-qiang，LIU Chang-qing． Heat transmission science[M]．Beijing： China Water Power Press，2010：19-21．(In Chinese)

[13]ROBINSON K. IC engine coolant heat transfer studies[D]．Bath, UK： University of Bath， 2001．

[14]邓帮林，刘敬平，杨靖,等．某缸盖热机疲劳分析[J]．湖南大学学报：自然科学版，2012，39(2)：30-34．

DENG Bang-lin，LIU Jing-ping，YANG Jing，etal．The thermal mechanical fatigue analysis on a cylinder head[J]．Journal of Hunan University：Natural Sciences，2012，39(2)：30-34．(In Chinese)

[15]任志俊，薛国祥．实用金属材料手册[M]．南京：江苏科学技术出版社，2007：950-956．

REN Zhi-jun，XUE Guo-xiang． Practical handbook of metal materials[M]．Nanjing： Jiangsu Science and Technology Press，2007：950-956．(In Chinese)

An Analysis on Thermal Load of Cylinder Head Based on Two-phase Flow Boiling Heat Transfer

YANG Jing1,2†, ZHANG Si-yuan1,2, LIU Kai-min1,2, WANG Yi1,2,GUO Hua-li1,2, SUN Cheng1,2,LI Ke1,2

(1. State Key Laboratory of Advanced Design and Manufacturing for Vehicle Body, Hunan Univ, Changsha, Hunan 410082,China;2. Research Center for Advanced Powertrain Technology, Hunan Univ,Changsha, Hunan 410082,China)

To study the temperature field distribution of engine cylinder head more precisely, based on the Euler multi-phase model, a new two-phase flow model combining the Rohsenow core boiling heat transfer model was established, which can be used for the numerical simulation of subcooled boiling. Applying BDL and Rohsenow transfer models separately, the cylinder head fluid-solid coupling heat transfer system was simulated and analyzed with the CFD technology. The results have shown that the Rohsenow core boiling heat transfer model is more precise than the BDL model in calculating the temperature field of engine cylinder head. The highest temperature of the cylinder head is 192.22 ℃, and the maximum of stress is 235 MPa, both of which can meet the strength requirements of cylinder head materials.

cylinder head; temperature field; two-phase flow; boiling heat transfer

1674-2974(2015)08-0034-06

2014-04-01

国家高技术研究发展计划(863计划)资助项目 (2012AA111703)；湖南省研究生科研创新项目 (CX2015B088)

杨 靖(1957-)，女，湖南益阳人，湖南大学教授，博士生导师

†通讯联系人，E-mail:yangjing10@vip.sina.com

TK412.2

A