基于秩和检验和广义线性模型的单病种结算研究*
罗开明吴黎军
基于秩和检验和广义线性模型的单病种结算研究*
罗开明1吴黎军2△
目的结合影响单病种费用的多个因素,研究单病种的分类问题,并预测各分类的费用。方法分别通过秩和检验和广义线性模型对所选因素进行剔除和各因素分类的差异性进行检验,对于没有显著差异的分类进行合并,并比较两种方法的结果;利用剔除和合并后的数据用广义线性模型预测费用。结果精简了单病种分类,预测了相应的费用;秩和检验和广义线性模型的参数检验的因素剔除和分类的合并结果基本一致(6种病有4种全相同,另外两种差别不大)。结论不考虑患者差异性而按照统一标准结算是不合理的,两种方法在很大程度上减少了病种的分类,具有一定的现实意义。
秩和检验 广义线性模型 单病种结算
为实现广大人民群众“看得上病、看得起病、看得好病”的新时期卫生工作服务宗旨,必须改革现行付费方式,由原来的按项目付费,逐渐过渡到按病种付费[1]。事实证明,按病种支付的实施在一定程度上减少了医疗服务中的不合理消费,降低了平均住院天数[2-5]。
本文比较秩和检验与广义线性模型这两种方法对剔除因素及合并分类的结果。利用剔除因素和合并分类后的数据,运用广义线性模型计算各因素分类对病种费用的影响大小,给出了各分类的费用。最后,同样的方法运用于其他病种。
理论基础和数据来源


广义线性模型:设(Yi;Xi1,Xi2,…,Xip)(i=1,2,…,n)为因变量Y与自变量X1,X2,…,Xp的观测值,若
(1)Y1,Y2,…,Yn相互独立,且对于每个i,Yi服从指数分布族;
(2)对于某单调、可微的连接函数g(·),有
其中μi=E(Yi),βi为模型参数(i=1,2,…,n),则称Y与X1,X2,…,Xp服从广义线性模型。
2.数据来源[7]:选取乌鲁木齐市三级医院两年的医疗保险数据,包括病人的性别、年龄、手术费、医保报销费用、自付费用等信息,选取医保报销费用作为应变量,性别、年龄、手术作为自变量,剔除异常值,然后进行分析。变量说明:手术(0表示不手术,1表示手术),性别(1表示男,2表示女)年龄分段(1表示44岁以下为青年人,2表示45岁至59岁为中年人,3表示60岁至74岁为年轻老年人,4表示75岁至89岁为老年人,5表示90岁以上为长寿老人)。
影响因素和分类的显著性检验
1.秩和检验:利用SAS9.2软件[8],对高血压的性别、年龄、手术分别秩和检验,判断分类的显著性,对于没有显著差异的分类进行合并,结果见表1。
由表1的P值表明(检验水准取α=0.01,下同):男女之间没有显著性差别;年龄3和年龄4之间没有显著差异;年龄4和年龄5之间没有显著差异。所以,将性别剔除,将年龄3、4、5合并,记为年龄345,保留手术。就合并后的年龄进一步检验,结果见表2。
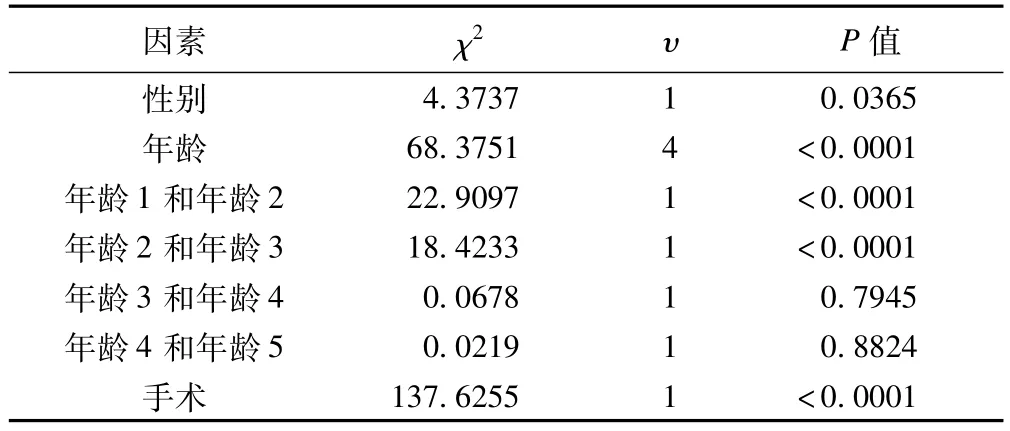
表1 高血压的Kruskal-Wallis检验

表2 高血压合并后年龄Kruskal-Wallis检验
由表2的P值表明:年龄3、4、5之间没有显著差异,进一步说明它们应该合并;年龄2和年龄345之间有显著差异。综合表1和表2的结果,我们对费用的影响因素进行筛选:剔除性别因素,保留手术,将年龄归为年龄1、年龄2、年龄345三类。
2.广义线性模型:我们利用SAS9.2软件,运用广义线性模型,对高血压数据进行分析,选择对数连接和Poisson分布,记为模型1,结果见表3。表3的P值表明:性别、年龄各分类的P值都大于0.01,说明显著性检验都不通过。可以说模型1的效果不好,需要对模型变量进行筛选。
对模型1进行TYPE 1、TYPE 3检验,结果如表4、表5。TYPE1型检验中,性别的P值为0.2523大于0.01,说明性别对高血压的费用没有显著影响。TYPE3型检验中,性别的P值为0.2523大于0.001,说明剔除性别对高血压的费用没有显著影响。
对分类之间的显著性检验,我们认为估计参数之间没有显著性差别,则可以将这几类合并为一类。通过CONTRAST以及不同的设计矩阵就可检验各个因素分类之间的差异性,结果见表6。
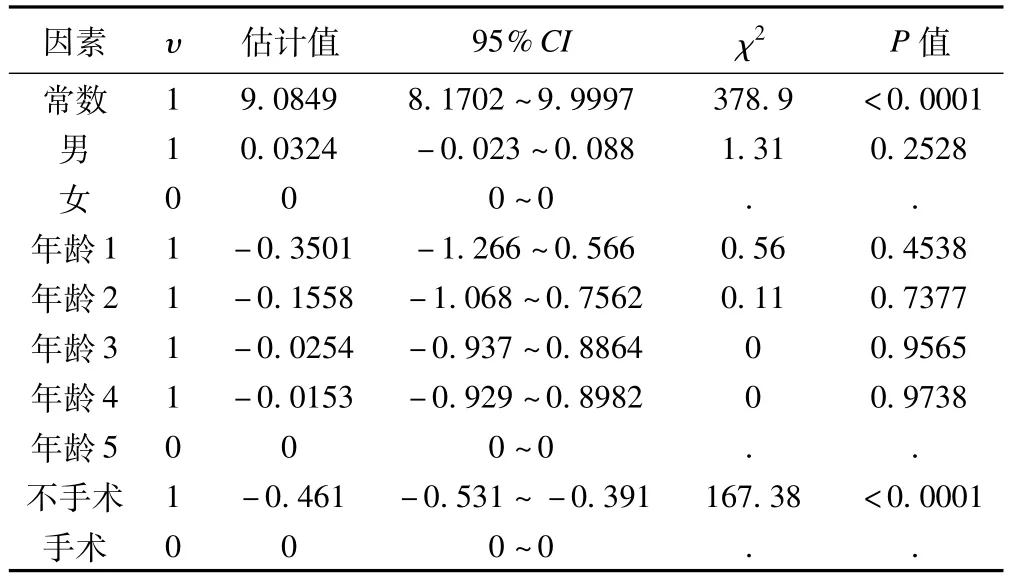
表3 模型1参数估计表
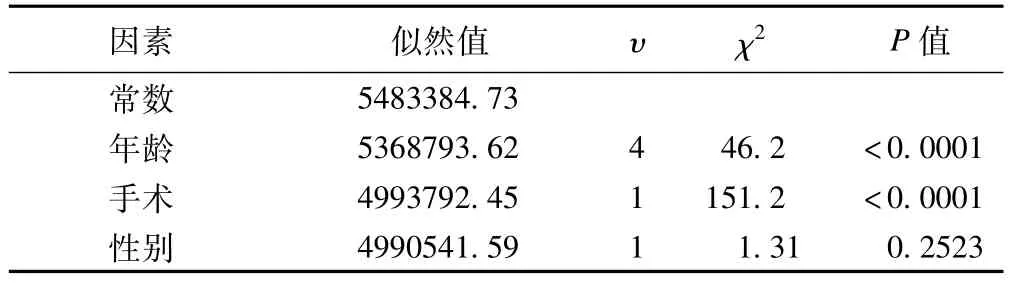
表4 模型1的TYPE 1型检验

表5 模型1的TYPE 3检验
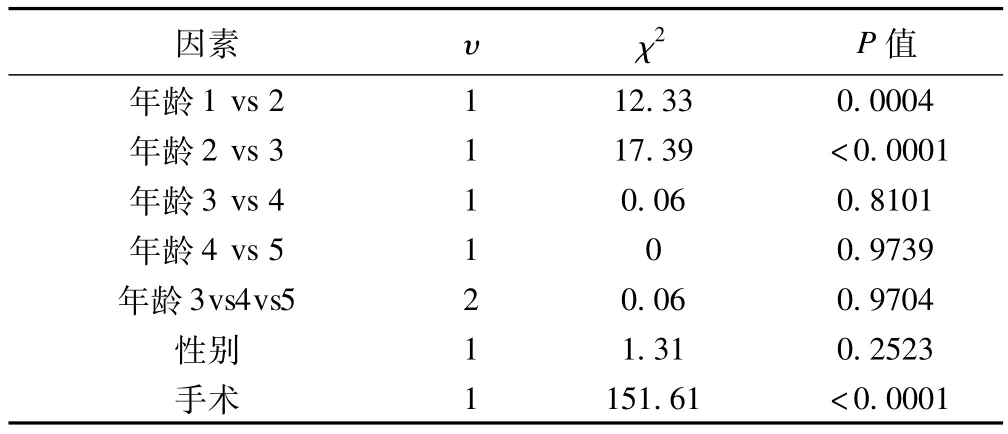
表6 模型1的参数配对检验表
表6的P值表明:在显著性水平为0.01时,年龄3和年龄4之间没有显著性差别;年龄4和年龄5之间没有显著性差别;年龄3、年龄4、年龄5之间没有显著性差别;性别之间没有显著性差别。综合表4、表5、表6,我们将性别因素剔除,将年龄3、4、5合并,记为年龄345,保留手术。
秩和检验和广义线性模型对病种的分析结果表明:这两种方法对高血压分类是一致的。如果按照原本性别2类,年龄5类,手术2类的分类总计20类,这样直接分类种类过多,是不合理的。所以需要对分类进行合并,合并后为6类,单病种结算的类别就大大减少了。后续分析选取:年龄、手术做为自变量。
广义线性模型计算费用
利用高血压剔除因素和合并分类后的数据,用广义线性模型计算病种费用及分析因素与分类对费用的影响大小,选取对数连接和分布,记为模型2。医保报销费用为应变量,手术(手术、不手术)、年龄(年龄1、年龄2、年龄345)为自变量。SAS 9.2拟合模型2,参数估计及显著性检验如表7。

表7 模型2参数估计表
表7中所有参数的P值都小于0.0001,说明每个参数都对费用有影响。

表8 模型2 TYPE 1检验表

表9 TYPE3检验表
表8、表9中TYPE1、TYPE3检验中年龄和手术的P值都小于0.0001,说明它们对费用有显著性影响。所以模型2比较合理。用模型2对高血压进行分类和计算费用如表10。
高血压费用为6类,费用栏各类费用差别较大,可以看出分类具有差异性,进一步说明前面的分类是合理的。年龄1的乘数因子exp(-0.321)=0.725,年龄2的乘数因子为exp(-0.132)=0.876,年龄345的乘数因子为1,可知60岁以上的年龄345人群医保报销费用的最多,45岁到59岁的年龄2人群次之,44岁以下的年龄1人群最少。不手术的乘数因子为exp(-0.46)=0.631,手术的乘数因子为1,因为手术的费用在医疗费用中占的比例较大。用同样的方法对冠心病、糖尿病、慢性胃炎、慢性支气管炎、腰椎间盘突出分析,结果如表11。
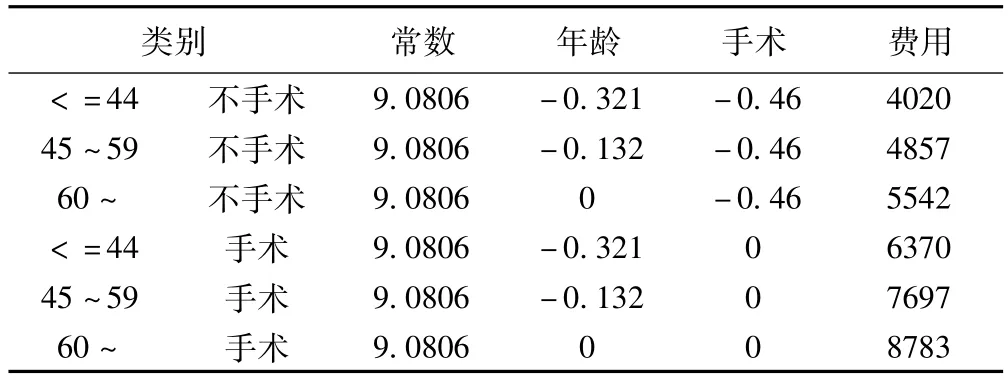
表10 高血压参数估计及费用计算(单位:元)

表11 五种病的结果比较
由表11结合前面的高血压分析结果可知,分别通过秩和检验和广义线性模型对本文6种病种的分类结果:一致的有高血压、慢性胃炎、慢性支气管炎、糖尿病4种;不一致的为腰椎间盘突出和冠心病2种。即使不一致也是很少的区别,腰椎间盘突出中秩和检验将年龄2、3、4合并为一类,而广义线性模型则将年龄3、4合并;冠心病秩和检验剔除了性别和年龄,而广义线性模型只剔除了年龄。手术在两种方法分类中都有,可以看出手术对费用有影响;年龄对费用也有影响,不同病种,年龄的分段不一样;性别对费用的影响不太显著(性别基本上都是剔除掉的)。
结 论
本文考虑了影响费用的多个因素,并运用秩和检验和广义线性模型对不同因素、各因素分类之间对费用影响的显著性进行检验。秩和检验是一种常见的非参数检验方法,主要用于检验样本间的差异性,优点在于不需要考虑样本服从什么分布,广泛运用于医疗、卫生等领域,简单易行。广义线性模型是经典线性模型的扩展,其应变量不再限制在正态分布,而是扩展到指数分布族,通过连接函数将自变量和应变量之间的关系设定为非线性关系,这不仅为拟合属性变量和取值为特定区间的变量提供了可能,同时更加符合实际中自变量与应变量之间的更为复杂的非线性关系,相对复杂。建议用广义线性模型对单病种的影响因素进行剔除,用秩和检验对各个因素的分类进行合并,最后用广义线性模型预测费用。
[1]林雪,齐颖,李思飞,等.积极探索案并汇总付费方式的改革.中国卫生经济,2004,8(8):45-46.
[2]徐长妍,于双成,迟宝荣.单病种限额付费挑战医院管理模式.中国医院管理,2007,07:5-7.
[3]吴萍,王瑛.医疗保险单病种结算标准的研究.中国卫生统计,2013,30(2):265-266,269.
[4]许永建,任建萍,卫萍,等.终末期肾病单病种付费实施现况及个人支付费用影响因素研究.医学与哲学,2014,35(4):95-96,封3.
[5]杨树东,张晓,沈其君.我国医疗保险制度中实行单病种付费的思考.东南大学学报(医学版),2006,1,25:47-49.
[6]娄冬华.秩和检验的统计思想.中国卫生统计,2005,04:264-265+267.
[7]黄雪毅,吴迪,吴黎军.医疗机构单病种付费研究.中国卫生统计,2014,3:468-470.
[8]杨池然,仲文明,周志勇.SAS 9.2从入门到精通.电子工业出版社,2008年11月.
[9]杨云鹏.广义线性模型,广义线性混合模型及其应用.新疆大学,2010.
[10]康萌萌.广义线性混合模型及其SAS实现.统计教育,2009,10:50-54.
(责任编辑:邓 妍)
国家自然基金地区项目(项目编号:11361058)
1.新疆大学数学与系统科学学院(830046)
2.新疆大学数学与系统科学学院统计教研室
△通信作者:吴黎军,E-mail:xjmath@xju.edu.cn

