生长曲线构建的不同方法比较*

刘 裕何健荣郭 勇夏晓燕王 平莫伟健卢锦华李伟栋于 佳林穗方冯 琼邱 琇△

生长曲线构建的不同方法比较*

刘 裕1，2何健荣1郭 勇1夏晓燕1王 平1莫伟健1卢锦华1李伟栋1于 佳1林穗方1冯 琼1邱 琇1△

目的寻找适合于构建人体测量指标生长标准曲线的方法和途径。方法以构建广州市胎龄别新生儿出生体重百分位曲线为例，从Tukey方法、稳健性回归和高斯混合模型等三种异常数据识别和剔除方法中获得最佳数据预处理效果，然后对比三次样条方法、LMS方法和GAMLSS方法对百分位数曲线构建的影响。结果高斯混合模型对多峰分布数据中的主要分布识别比较理想，而对单峰分布，稳健性回归比Tukey方法更加可靠。而从拟合优度以及小于胎龄儿（SGA）、大于胎龄儿（LGA）的识别能力看，GAMLSS构建的胎龄别新生儿出生体重百分位曲线比三次样条和LMS方法估计精度更高。结论数据预处理过程应根据数据分布的特点选用合适的异常值识别和剔除方法，而曲线光滑过程中，GAMLSS方法可以对四阶矩进行建模，得到的百分位数曲线平滑且误差更小。

生长曲线 Tukey方法 稳健性回归 高斯混合模型 LMS方法 GAMLSS

医学参考值范围是临床实践中筛查异常情况的重要依据。当测量指标依赖于其他协变量（如年龄）时，应制定随协变量变化的参考值曲线，例如儿童青少年的身高、体重、体质指数、血压、肺功能等生长参考值曲线［1－4］。构建参考值曲线的关键是对原始数据进行预处理并采用合适的统计学方法描绘曲线。尽管目前有多种统计学方法可用于曲线的构建，但不同的数据处理和统计学方法对曲线构建产生的影响，鲜有文献报道。本文拟利用广州市新生儿出生体重数据，对此进行探讨，并提出方法选择的建议。

资料来源

本研究的数据来源于广州市围产保健－产时管理软件。该系统自2000年启用，由广州所有助产机构录入在院内分娩产妇及新生儿的出生及围产期信息，并用于核发出生医学证明。数据质量控制每季度由市区两级妇幼保健院完成。本研究纳入2009年1月至2011年12月出生胎龄在26～43周的单胎活产男孩资料。考虑到26～33周胎龄儿数量较少，将2007年1月至2008年12月期间出生的26～33周胎龄儿纳入分析。

方 法

1．胎龄的确定

依据广州市助产技术管理规范，新生儿胎龄用妊娠16周前B超检查测定的头臀径或双顶径进行确定；无法获得B超检查结果者，胎龄由末次月经结合出生后胎龄评估确定。胎龄以整周表示。

2．异常值识别

胎龄的错分和出生体重的极端值会给胎龄别出生体重百分位数曲线的构建带来偏移［3－7］，具体表现为，胎龄别出生体重呈不对称、双峰或长尾分布，需要首先识别和剔除。针对不同的分布特征，常用的识别异常数据的稳健性统计方法包括Tukey法［5－6］、稳健性回归（Robust regression）［3－4］和高斯混合模型（Gaussian m ixturemodel）［3，7］。为了比较不同异常数据处理方法对生长曲线构建的影响，分别采用Tukey法和高斯混合模型进行数据预处理，计算胎龄别出生体重的第10、50和90百分位数曲线。由于高斯混合模型仅用于多峰分布的情形，对35周后的体重数据采用稳健性回归方法。三种方法的原理如下：

Tukey方法 对每个胎龄x的出生体重数据y，首先计算第1四分位数（Q1）、第3四分位数（Q3）及其四分位数间距（IQR＝Q3－Q1）；然后计算L统计量，以反映两端的体重数值距离Q3或Q1的距离是IQR的多少倍：（1）若y＞Q3，L＝（y－Q3）／IQR；（2）若y∈［Q1，Q3］，L＝0；（3）若y＜Q1，L＝（Q1－y）／IQR。如果L的绝对值超过给定的临界值，则认为是异常值。临界值的设定一般在1．5～3．0，通常认为取2．0附近的界值是合适的［5］。

稳健性回归 假定某个胎龄x的新生儿出生体重y服从正态分布，稳健性回归可用于识别数据中的异常值。常用的基于M估计的稳健性回归通过最小化目标函数获得未知参数的估计，其中n代表样本量，ei表示残差；特别地，ρ（e）＝e2对应参数的最小二乘估计。统计上，通过迭代再加权最小二乘方法获得参数的估计值，每次迭代时残差超过标准差的给定倍数的值将被识别为异常值，并从下次计算中剔除，直至估计的参数收敛。世界卫生组织（WHO）建议年龄别体重资料异常值的排除标准为4个标准差［8］。

高斯混合模型 针对数据双峰的特点，假定某个胎龄x的新生儿出生体重y为两个正态分布的复合分布f：一个为主要分布fp，另一个为次要分布fs，即f＝q·fp＋（1－q）·fs，其中，q代表样本属于这两个正态分布的权重比例。这样，观测（x，y）属于主要分布fp的概率为π＝q·fp／f。若π＞0．5，则认为（x，y）来自于主要分布，否则认为（x，y）为异常数据［3，7］。

3．曲线构建

获得“干净”数据后，直接使用各胎龄别数据的百分位数构建参考曲线比较粗劣。因此，常采用非参数方法或参数方法进行曲线平滑。非参数方法指各种统计平滑法，如三次样条平滑［6］。最常用的参数方法莫过于Box－Cox指数－中位数－变异系数（lambdamedian－sigma，LMS）法［2，9，10］，并进一步推广为基于位置参数、尺度参数和形状参数的广义可加模型（generalized additive model for location，scale and shape，GAMLSS）［6，11－12］。

（1）三次样条方法 假定有n对测量值（xi，yi）（i＝1，…，n）且α≤x1≤x2≤…≤xn≤b，三次样条函数f（x）定义为［a，b］上的函数，满足：①f（x）在每个［xi，xi＋1］具有三次多项式形式f（x）＝β0i＋β1i（x－xi）＋β2i（x－xi）2＋β3i（x－xi）3；②f（x）及其前二阶导数在xi连续。最小化惩罚性残差平方和得到f（x）的惩罚性最小二乘估计，这里，λ（λ＞0）为给定的常数，在人体测量值拟合时取0．2左右是合适的［1］。

（2）LMS方法 LMS方法采用Box－Cox变换将胎龄别出生体重转换为正态数值［10］。这个过程包括：估计每个胎龄t的三组模型参数，即正态转换指数、体重中位数和变异系数；然后用三次样条拟合三组参数获得光滑的参考曲线。Cole和Green（1992）用Fisher得分法最大化惩罚性似然函数获得光滑参数和模型参数的迭代估计。百分位数曲线表示为

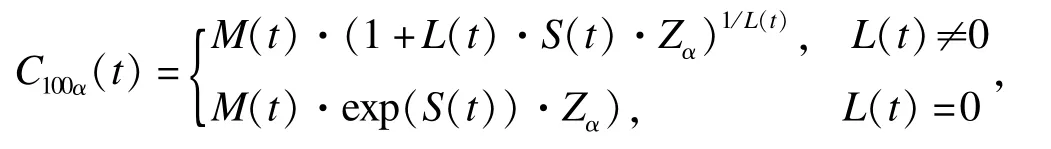
Zα是标准正态分布的下百分位数。

（3）GAMLSS方法 GAMLSS方法允许对各种峰态非对称分布进行建模并估计光滑的百分位数［11］。基于Box-Cox幂指数（Box-Cox power exponential，BCPE）分布的GAMLSS方法包含四个参数μ、σ、v和τ，分别对应胎龄别出生体重y的位置参数、尺度参数、偏度和峰度。GAMLSS对这些参数进行建模，g1（μ）＝h1（x），g2（σ）＝h2（x），g3（v）＝h3（x），g4（τ）＝h4（x）。其中，gi是对应参数的单调连接函数，如μ的恒等函数或对数函数；hi是关于协变量的参数或非参数函数，如时间t的线性函数或三次样条函数。Rigby和Stasinopoulos（2005）采用Fisher得分算法最大化惩罚性似然函数进行光滑参数和模型参数的迭代估计，基于模型参数的估计值，可以用y的Z得分值获得其任意百分位数估计。最近的研究建议使用对数连接函数对胎龄别出生体重构建百分位数曲线［12］。

4．拟合效果评价

采用赤池信息准则（Akaike information criteria，AIC）和残差均方比较百分位数的拟合效果。其中，残差均方定义为拟合的百分位数（P3，P10，P25，P50，P75，P90，P97）与实际值之差的平方和除以比较的百分位数的个数［2，15］。

5．统计软件

本研究所有统计计算和建模过程均通过R软件（Version 2．15．0，http：／／www．r－project．org）实现。

结 果

剔除缺失数据后，共纳入167 288个初产单胎男孩的出生数据进行分析。从图1看出，26～34周出生的新生儿，胎龄别出生体重呈明显的双峰分布或偏态分布。随着胎龄的增加，双峰分布逐渐消失，分布的对称性有所改善。表1用统计数字特征描述了各个胎龄出生体重的分布情况。

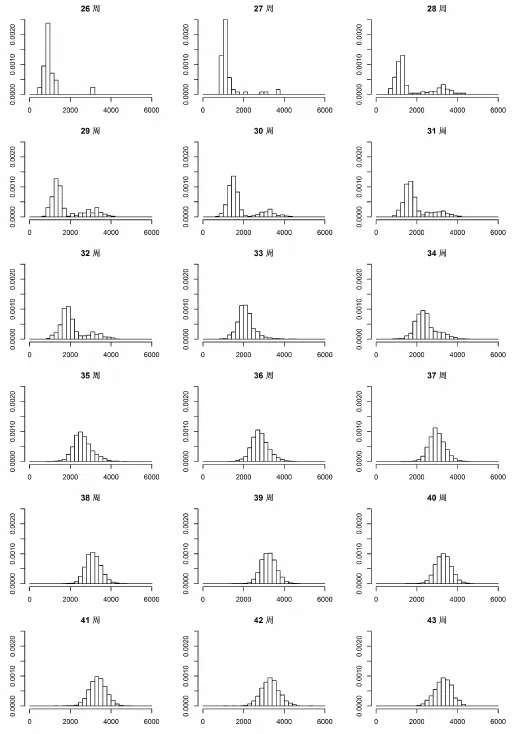
图1 单胎初产男婴不同胎龄出生体重分布图

以剔除尽可能少的异常点但又能捕获分布的主要特征为基本依据，选取Tukey方法L统计量界值为2．0，高斯混合模型主要分布概率界值π为0．5，稳健性回归界值为双边概率1／10000的3．89个标准差。最终，高斯混合模型在26～34周剔除18．9%（734／3885）的异常点，稳健性回归在35～43周剔除0．9%（1493／163403）的异常点；而Tukey方法在26～34和35～43分别剔除5．9%（915／3885）和0．7%（1221／163403）的异常点。

图2显示了异常值剔除后胎龄别出生体重分布。其中，高斯混合模型有效地捕获了26～34周出生的新生儿体重分布，Tukey方法在37～43周出生新生儿体重极端值的识别与稳健性回归相近，均接近于剔除前的初始分位数。而从表1中35～36周出生新生儿体重的偏度和峰度系数来看，稳健性回归更有效地剔除了由于孕周错分导致的异常值。

图3显示了异常值剔除前后三次样条光滑、LMS和GAMLSS三种方法拟合的胎龄别出生体重百分位数曲线。异常值剔除前，三种方法在35～43周的拟合结果相近，拟合值均接近于初始百分位数；但在26～34周，初始百分位数显示小孕周出生体重较大孕周分散，提示存在系统误差。异常值剔除后，三者拟合的曲线形状相近，LMS和GAMLSS曲线的平滑效果优于三次样条方法，尤其表现在26～27周样本量较少的一段。表2比较了三种方法的拟合优度及用三种曲线划分SGA和LGA的效果。AIC统计量及残差均方均显示GAMLSS方法的拟合效果与LMS方法相近，且优于三次样条方法；但GAMLSS方法对SGA和LGA的判定更接近10%，因此拟合效果最好。比较图3异常值剔除前后的拟合结果可见，异常值剔除主要纠正了26～34周各胎龄出生体重右尾部的分位数。

表1 三种异常值剔除方法胎龄别出生体重比较

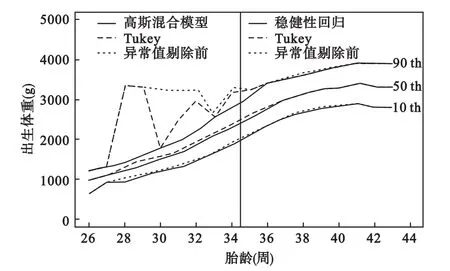
图2 三种异常数据剔除方法对胎龄别出生体重百分位数曲线构建的影响

表2 不同方法构建的参考曲线的拟合优度及SGA、AGA和LGA的分布

图3 不同方法构建的参考曲线效果比较

讨 论

在临床应用中，出生体重参考曲线判别异常情况的能力备受重视。胎龄的错分和出生体重极端值不仅影响参考曲线初始百分位数的估计，也会影响随后的参考曲线平滑或建模［4，13］。本研究显示，高斯混合模型较好地识别了多峰分布中的主要分布；Tukey方法和稳健性回归对正态分布数据极端值的识别能力和效果比较接近；当数据呈现偏态和峰态分布时，稳健性回归对异常数据的识别能力较好。因此，基于数据的分布特点和异常值的产生原因选用不同的方法，有利于改善异常数据的有效识别。

参考曲线构建时，利用三次样条方法直接对分位数的经验估计值进行平滑，方法直观且对数据的分布假设较少，拟合结果接近经验分位数，但效果并不理想，尤其是经验百分位数曲线不够光滑时，平滑效果较差［13］。采用惩罚性似然估计的LMS方法构建参考曲线已经得到广泛验证，即便出现随时间变化的偏度系数，LMS方法得到的百分位数曲线也是可靠的。而且，LMS方法得到的L、M和S曲线能够很好地反映观测值的分布特征，便于更好地认识数据的深层结构。但是，如果观测数据既呈偏态又呈峰态分布时，Box－Cox正态变换效果欠佳［11］。GAMLSS方法允许对中位数、标准差、偏度系数和峰度系数等四阶矩进行建模，能够极大地提高估计的精度；它的另一个优势在于可以对胎龄、性别、产次等其他协变量进行建模，从而能在一个模型中使用全部数据，获得样本量较小分组的分布曲线的稳健估计［12］。

同其他统计建模一样，生长曲线构建过程中参数的选择至关重要。异常数据识别时，虽然没有金标准，但剔除尽可能少的样本而又能捕获数据的基本特征成为广泛采用的标准［3，6］；曲线构建的参数选择，采用拟合优度统计量可方便地进行方法内和方法间拟合效果比较［9］。本文在异常值识别充分参考了文献相关方法的参数选择范围，应用于本研究并进行异常值识别比例和剔除前后数据分布的比较。曲线构建时，我们也尝试了0．1～0．4的其他光滑参数，平衡曲线光滑效果和拟合优度后选取了0．2；GAMLSS拟合时，我们也尝试了恒等函数作为连接函数，但AIC统计量明显比对数函数时大得多。最后，我们还比较了三种方法对SGA和LGA的识别能力，发现GAMLSS方法能够识别9．58%的出生婴儿为SGA，10．09%的为LGA，与国际上其他研究相近［14］。

新生儿出生体重仅仅是儿童生长发育指标的一个代表，本文阐述的参考曲线构建中常用的数据剔除和建模方法，可以推广到其他生长曲线的构建，建模过程中统计方法的选择和评价也可为其他相关工作提供参考。

［1］尚磊，徐勇勇，侯茹兰，等．采用三次样条函数拟合体重百分位数曲线．中国卫生统计，2001，18（5）：266-268．

［2］江梅．LMS法：一种适用建立肺功能全年龄段正常参考值曲线方法．中国卫生统计，2013，30（5）：766-768．

［3］He J，Xia H，Liu Y，et al．A new birthweight reference in Guangzhou，southern China，and its comparison with the global reference．Archives of diseases in childhood．2014：doi：10．1136／archdischild-2013-305923．

［4］Foster PJ，Kecojevic＇T．Reference Grow th Charts for Saudi Arabian Children and Adolescents．In：Vinod HD．Advances in Social Science Research Using R．New York：Springer，2010：107-128．

［5］Arbuckle TE，W ilkins R，Sherman GJ．Birth weight percentiles by gestational age in Canada．Obstetrics and gynecology，1993，81（1）：39-48．

［6］Bonellie S，Chalmers J，Gray R，et al．Centile charts for birthweight for gestational age for Scottish singleton births．BMC pregnancy and childbirth，2008，8：5．

［7］Liu Z，Zhang J，Zhao B，et al．Population-based reference for birth weight for gestational age in northern China．Early human development，2014，90（4）：177-187．

［8］Centers for Disease Controland Prevention．Cut-offs to define outliers in the 2000 CDC Grow th Charts．Available from：http：／／www．cdc．gov／nccdphp／dnpa／grow thcharts／resources／BIV-cutoffs．pdf

［9］Flegal KM．Curve smoothing and transformations in the development of grow th curves．The American journal of clinical nutrition，1999，（1）：163S-165S．

［10］Cole TJ，Green PJ．Smoothing reference centile curves：the LMS method and penalized likelihood．Statistics in medicine．1992，11（10）：1305-1319．

［11］Rigby RA，Stasinopoulos DM．Generalized additivemodels for location，scale and shape．Applied statistics，2005，54：507-554．

［12］Cole TJ，Statnikov Y，Santhakumaran S，et al．Birth weight and longitudinal grow th in infants born below 32 weeks’gestation：a UK population study．Archives of disease in childhood-fetal and neonatal edition，2014，99：34-40．

［13］Ramos F，Perez G，Jane M，et al．Construction of the birth weight by gestational age population reference curves of Catalonia（Spain）：Methods and development．Gaceta santitaria，2009，23：76-81．

［14］Olsen IE，Groveman SA，Lawson ML，et al．New intrauterine grow th curves based on United States data．Pediatrics，2010，125：e214-224

（责任编辑：郭海强）

Com parison of Statistical Methods for the Construction of Grow th Reference Curves

Liu Yu，He Jianrong，Guo Yong，et al．（GuangzhouWomenandChildren’sMedicalCenter（510623），Guangzhou）

ObjectiveTo find out amethod to construct grow th curves for various anthropology measurements．MethodsIllustrated by the construction of a new birth weight reference for gestational age in Guangzhou，the best data pre-processing procedure was determined for outlier detection and removal after comparing with 3 differentmethods：Tukey’smethod，robust regression and Gaussian mixture model．Then cubic spline，LMS and GAMLSS were compared for the construction of grow th curves．ResultsGaussianm ixturemodel had an outstanding performance in the detection of outliers for datawithmultimodal distribution and compared with Tukey’smethod，robust regression seemedmore reliable for the unimodal asymmetric data．In the construction of centile charts，GAMLSSmodel gavemostaccurate estimate compared with cubic spline and LMSmethod．ConclusionMethods based on the distribution characteristics should be used for data pre-processing．The fourthmoment of the distribution can bemodeled by GAMLSS，so grow th curves fitted by GAMLSS aremuch smoother and the fitting errors are much fewer．

Grow th curve；Tukey’smethod；Robust regression；Gaussian mixturemodel；LMS；GAMLSS

*：广州市科技计划重大科技专项（2011Y2－00025）；广州市科技计划国际科技交流与合作专项（2012J5100038）

1．广州市妇女儿童医疗中心（510623）

2．中山大学数学与计算科学学院统计系

△通讯作者：邱琇，E-mail：qxiu0161＠163．com