复杂抽样数据统计分析方法回顾*

姜 博王丽敏刘 艳△李镒冲△

复杂抽样数据统计分析方法回顾*

姜 博1王丽敏2刘 艳1△李镒冲2△

当今社会科学与健康科学调查研究，尤其是大规模调查，往往涉及多地区或多中心的抽样问题，采取单纯随机抽样选择样本因调查对象过于分散，成本高，可行性低［1］，调查设计者更倾向于可行性较高的复杂抽样，但其通常使样本结构复杂化。若采用忽略抽样特征的传统统计学方法分析此类数据，会导致标准误的低估，进而低估可信区间，且增大犯I类错误的可能性，最终导致偏倚甚至得到错误的统计推断［2］。目前，对于复杂抽样数据的统计分析主要分为基于设计和基于模型两种方法体系［3］，本文对这两种分析体系的主要文献进行了回顾。

复杂抽样简介

复杂抽样指在抽样过程中采用除一阶段单纯随机抽样外，其他抽样方法或其组合的抽样方案。复杂抽样通常具有分层、整群、不等概率或多阶段等设计特点，其产生的样本称为复杂样本。复杂抽样优势在于：节省人力物力，使大规模调查更具可行性；可灵活调整样本量在各级抽样单位中的分配；可通过改变抽样比来提高子总体的代表性和估计的可靠性。因此，目前在卫生领域调查研究中，复杂抽样设计已非常普遍［4］，许多大规模国家级调查均采用了复杂抽样设计，如2010年中国慢性病及其危险因素监测［5］、美国全国健康及营养状况调查［6］等。

复杂样本结构

复杂抽样设计往往使样本具有明显层次性，即样本信息在一定地理区域或范围内存在聚集性［7］，其内个体彼此不独立。以2010年慢性病及其危险因素监测多阶段复杂抽样设计为例：第一阶段在所有162个监测县／区中按不等概率方法（与人口规模成比例的抽样方法，PPS）随机抽取4个乡镇；第二阶段在每个抽中的乡镇中利用PPS法随机抽出3个村；第三阶段在每个抽中的村中利用整群抽样随机抽取居民户；第四阶段从抽中的居民户中随机抽取1名符合条件的居民作为调查对象［5］。四个阶段抽样将样本分为5个水平，1水平是居民，2水平是居民户，依次类推，每个水平包含多个抽样单位即乡镇是县／区的抽样单位，依次类推。生活在同一水平、单位间的居民因有相同的经济、环境等因素，常具有相似的生活习惯，使得居民个体观测指标数据有明显层次聚集性，这种数据称为层次结构数据。这种现象广泛存在于自然界和人类社会中，卫生领域大规模调查更是无法避免接触此类数据。因此，能够解释复杂样本层次结构的统计分析方法就显得尤为重要。

复杂样本分析方法

针对复杂样本，目前有两种统计分析方法体系，即基于设计和基于模型的统计分析方法，二者主要区别在于假设总体是否来自于一个无限的超总体［3］。前者不依赖于数据分布特征，通过对样本的抽样设计特点来分析并解释数据；后者则不考虑设计因素，利用相应模型假设进行分析［8］。

1．基于设计的统计分析方法

（1）描述性统计

基于设计的统计描述方法常结合权重进行构造，权重包括三个方面：抽样权重、无应答权重和事后分层权重［9］，可表示为：

ws为抽样权重，wr为无应答权重，wps为事后分层权重。抽样权重为入样单元被抽中概率倒数，若存在多阶段抽样，则为各阶段入样单元权重之积［10］。无应答权重为样本应答率倒数，可用与应答率相关变量分层计算。事后分层权重目的在于将样本特征调整与目标总体一致，其计算需将目标总体与样本按关键指标分层，分别计算各层目标总体总量与累计权重（抽样权重与无应答权重）之和，最终形式即每层总体总量与累计权重之比［11］。利用权重，均数可表示为：

率可表示为：

δi表示当第i个对象具有某特征，则δi＝1，否则δi＝0。

对于方差估计，主要包括泰勒级数线性近似法、刀切法、平衡半样本法［12］。泰勒级数线性近似法基本思想是利用泰勒级数方法将非线性统计量线性化，然后计算方差的估计值［2，9］。刀切法基本思想是将总体分成k组，每次抽取时从中去掉一组，得到的多个二次抽样样本，每个二次样本可得到一个均数或率的估计值，根据估计值的差异估计方差［13］。平衡半样本法基本思想是假设总体分成L层，从每层随机抽取两个样本单位，共抽取2L次，产生2L个半样本，得到多个均数或率的估计值，利用多个估计值的差异估计方差［12，14］。研究显示，泰勒级数线性近似法更为稳定［15］，应用范围更广［16］。为简化计算，SAS等统计软件应用泰勒级数线性近似法估计方差时一般只考虑初级抽样单元的数目，而忽略其他级别抽样单元［17］，当初级抽样单元抽样比例较小时，方差估计的偏倚也较小［18］。

基于设计的统计推断方法适合大样本层次结构数据，估计较为精确、稳定［8］，对于小样本数据、缺失数据等情况可能造成估计偏倚［3］。

（2）分析性统计（关系或效应估计）

基于设计的统计分析方法是将权重引入模型。若因变量为连续型变量，常用基于设计的线性回归模型。其模型参数估计方法根据伪极大似然法推导出［19］：

w表示权重，Y＝（Y1…Yn）T，XT＝（x1…xn）。

若因变量为分类变量，常用基于设计的logistic回归模型，其采用极大似然法估计参数，似然函数为［20－21］：

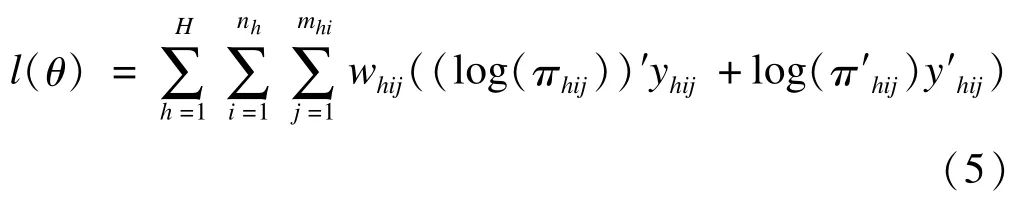
H为分层抽样层数，h＝1，2，…，H；i为第h层中第i单位，i＝1，2，…，nh；j为第h层中第i单位的第j个观测值，j＝1，2，…，mhi，h层中总计mhi个观测值；whij为权重；y为结局变量。以二分类为例，yhij表示y第一类的指示变量，y′hij表示y第二类的指示变量；πhij是y的期望向量。

基于设计的方法不足在于，需要足够样本量，即使大型调查研究中，也可能出现某些地区样本量较小导致结果不可靠；覆盖不全、无应答等情况导致抽样随机化假定被破坏，造成偏倚［16］。基于设计的统计分析方法应用较为广泛，如英国健康调查、英国社会态度调查等［22］。

2．基于模型的统计分析方法

（1）描述性统计

基于模型的方法通过拟合相应模型进行统计描述。对于计量资料，假设数据满足线性模型，Y＝β＋e且e～（0，δ），β的估计值即为样本均数，可用公式＝计算，采用正态近似法估计总体均数双侧可信区间为同理对于计数资料，假设数据满足二项分布概率模型，总体概率π的估计值p＝X／n，正态近似法估计总体概率双侧可信区间为p±uα／2Sp。

另一种描述方法是根据超总体模型理论，假设所研究的总体是随机从超总体中抽取的一个样本。对总体参数的统计推断转变为预测未抽中单元［23］，即在某种特定模型假设条件下，利用样本数据估计未抽到数据，进而估计总体参数［24］。

如公式所示，从总体中抽取样本S后，总体总和Y被分解为两个部分。其中是抽取到的样本集合属于未抽中部分，通过样本S拟合相应模型进行估计。通过此方法可以估计总体总和、均数、比率、方差等，具体计算方法可参考相关文献［3，23－24］，目前超总体模型在卫生领域的应用并不多见。

基于模型的统计推断方法可适用于小样本问题、数据缺失问题、离群值问题［3］，但其对模型的假设有较高要求，也无法很好描述层次结构数据［23］。

（2）分析性统计

基于模型的方法采用适当的模型来拟合数据，如线性模型、多水平模型等。多水平模型与传统模型（线性模型、logistic回归模型等）区别在于其将总的随机误差分解到相应水平中，每个水平都有与其误差项相应的残差、方差与协方差项，最终构建适应层次结构数据具有复杂误差结构的模型［25］。多水平模型中因变量可为定量或定性变量，以多水平logistic回归模型为例，拟合两水平随机效应模型［7］。

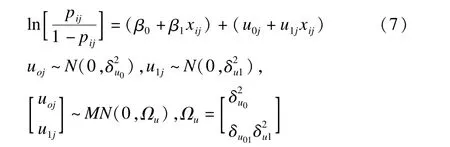
i为1水平；j为2水平；β0为平均截距，u0j为截距的随机变量；β1为平均斜率，u1j为平均斜率的随机变量；（β0＋β1xij）为固定效应，（u0j＋u1jxij）为随机效应，以迭代广义最小二乘法与边际拟似然法等方法估计参数。

因层次结构数据有聚集性特点，应用传统模型将导致各参数及方差估计不准确，并可能掩盖不同水平对反应变量的影响，导致错误结论［25］，而多水平模型可以有效将各水平作用分离出来，较精确地调整因不同水平个体间相关性对结果产生的偏倚［26］；可有效处理缺失值问题［27］。其不足在于，各水平单位数量不能太少；模型参数估计与假设检验较复杂［28］。多水平模型常用于注重区域影响作用的调查，如不同水平医学心理学调查研究［29］、不同地区儿童生长发育影响因素调查研究［30］等。

3．基于设计的模型辅助方法

若样本来自于不等概率的抽样设计，忽略设计特点可能导致估计的偏倚［31］。基于设计的分析方法虽考虑了权重的影响，但对数据的处理仅停留在一水平单位［32］，无法同时考虑各水平的影响，且对缺失数据较敏感。所以能够同时汲取二者优点，相互取长补短的方法具有较强的理论吸引力和应用价值。近20年来，许多统计学家积极探索基于设计的模型辅助方法，加权多水平模型（weighted multilevelmodels）即为其中重要的一部分。

加权多水平模型从抽样理论与多水平模型理论两个角度综合对层次结构数据进行分析，利用权重减小不等概率抽样在参数估计中产生的偏倚，又能同时分析多个水平单位的影响。加权多水平模型的模型结构与一般多水平模型相似，但加权多水平模型是利用伪极大似然估计法进行参数估计［33－34］：

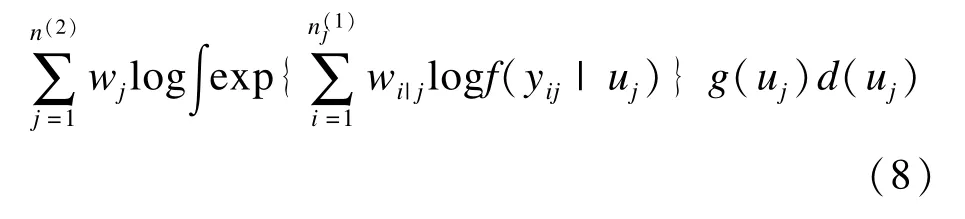
i为1水平，j为2水平，权重wj＝1／πj，wi｜j＝1／πi｜j，标准误可根据泰勒线性三明治法计算。模型中，需分别计算各水平权重，但如果样本量较少会导致伪极大似然估计产生偏倚，为减小偏倚可以调整权重。以两水平为例，目前权重缩放（scaling of weights）常用计算方法有两种，其一是Pfeffermann等于1998年提出，另一种是由Longford等于1995年提出［35］：

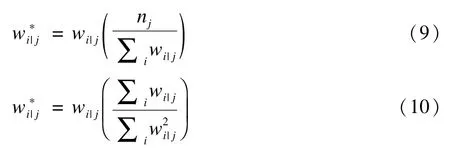
加权多水平模型可通过SAS 9．4版本GLIMMIX过程、Stata软件gllamm分析模块实现。目前由于权重的收集与计算较复杂、统计学软件支持较少等原因，加权多水平模型的应用较少，还处于推广之中。

结 论

目前公共卫生领域大规模调查研究中，复杂抽样的应用十分广泛，基于设计和基于模型的统计分析方法都可以普遍应用在复杂样本，有研究表明，在大样本的条件下，其估计结果相差不大［21］，可根据调查研究目的、抽样设计等因素选择相应的方法，在抽样框信息完整，样本量足够大的前提下，推荐使用基于设计的统计分析方法；抽样信息不完整时或更多考虑层次结构关系的前提下，推荐使用基于模型的统计分析方法。而加权多水平模型综合了两种方法优点即在统计分析时，不仅考虑抽样设计而且考虑层次结构关系，具有较大的使用价值和推广意义，可以为卫生及相关领域政策的制定提供更加全面、精确的参考。

［1］Warszawski J，Messiah A，Lellouch J，et al．Estimating means and percentages in a complex sampling survey：application to a French national survey on sexual behaviour（ACSF）．Stat Med，1997，16（4）：397-423．

［2］刘建华，金水高．复杂抽样调查总体特征量及其方差的估计．中国卫生统计，2008，25（4）：377-379．

［3］金勇进，贺本岚．复杂抽样推断方法体系的比较研究．统计与信息论坛，2011，26（10）：3-8．

［4］Osborne JW．Best Practices in using large，complex samples：The importance of using appropriate weights and design effect compensation．Practical Assessment，Research＆Evaluation，2011，16（12）：1-7．

［5］赵文华，宁光．2010年中国慢性病监测项目的内容与方法．中华预防医学杂志，2012，46（5）：477-479．

［6］ES Ford WHG，Dietz WH．Prevalence of themetabolic syndrome among US adults：findings from the third National Health and Nutrition Exam ination Survey．Jama，2002，287（3）：356-359．

［7］杨珉，李晓松主编．医学和公共卫生研究常用多水平统计模型．北京：北京大学医学出版社，2007：374-374．

［8］DCWheeler JEV，Paskett E．A Comparison of Design-based and Model-based Analysis of Sample Surveys in Geography．The Professional Geographer，2008，60（4）：466-477．

［9］West BT．Statistical and methodological issues in the analysis of complex sample survey data：practical guidance for trauma researchers．JTrauma Stress，2008，21（5）：440－7．

［10］胡楠，姜勇，李镒冲，等．2010年中国慢病监测数据加权方法．中国卫生统计，2012，29（3）：424-426．

［11］Little R．Post-stratification：a modeler′s perspective．J Am Stat Assoc，1993，88（423）：1001-1012．

［12］王晓荣，赵俊康，王彤．复杂抽样下的截取回归模型在医学研究中的应用．中国卫生统计，2012（5）：691-697．

［13］D Krewski JR．Inference from stratified samples：properties of the linearization，jackknife and balanced repeated replication methods．The Annals of Statistics，1981，9（5）：1010-1019．

［14］吕萍．重权数在复杂调查的方差估计中的应用．统计研究，2011（2）：93-99．

［15］Paben SP．Comparison of Variance Estimation Methods for the National Compensation Survey：Proceedings of the Section on Survey Research Methods，American Statistical Association，1999．［16］Statistics-stockholm gk-jofo．Models in the practice of survey sampling（revisited）．JOURNAL OF OFFICIAL STATISTICS-STOCKHOLM，2002，18（2）：129-154．

［17］SAS Institute Inc．2011．SAS／STAT？9．3 User′s Guide．Cary，NC：SAS Institute Inc．

［18］Rao J．Interplay between sample survey theory and practice：an appraisal．Survey Methodology，2005，31（2）：117-138．

［19］Li J．Regression Diagnostics for Complex Survey Data：Identification of Influential Observations．Ann Arbor：Proquest，2007：5-8．

［20］缪凡，童峰．复杂抽样数据的logistic回归分析方法及其应用．中国卫生统计，2008，25（6）：577-579．

［21］陈丹萍．广义线性混合效应模型（GLMM）与复杂抽样的logistic回归模型在分层整群抽样数据分析中的比较：复旦大学，2010．

［22］Rafferty A．Introduction to Complex Sample Design in UK Government Surveys．London：ESDSGovernment，2011：21-33．

［23］邹国华，冯士雍．超总体模型下有限总体的估计．系统科学与数学，2007，27（1）：27-38．

［24］艾小青，金勇进．有限总体的估计——基于超总体模型．统计教育，2009，（2）：3-6．

［25］孙振球主编．医学统计学（第3版）．北京：人民卫生出版社，2002：445-464．

［26］C Duncan KJ，Moon G．Context，composition and heterogeneity：usingmultilevelmodels in health research．SocSciMed，1998，46（1）：97-117．

［27］王艳梅，王洁贞，丁守銮，等．多水平模型在纵向研究资料中的应用．山东大学学报（医学版），2007，（7）：658-661．

［28］谷晓然．资本资产定价之收益率影响因素分析——基于多水平模型的实证研究：云南财经大学，2012．

［29］张岩波，张海敏，何大卫．多水平模型及其在医学心理领域中的应用．山西医科大学学报，2001，（6）：510-512．

［30］金芳，倪宗瓒，李晓松，等．多元多水平模型及其在儿童生长发育研究中的应用．中国卫生统计，2004，（04）：13-15．

［31］D Pfeffermann CJS，Holmes DJ．Weighting for unequal selection probabilities in multilevelmodels，1998，60（1）：23-40．

［32］Asparouhov T．Weighting for unequal probability of selection in multilevelmodeling．Mplusweb notes，2004（8）：1-28．

［33］SRabe-Hesketh．Multilevelmodelling of complex survey data．J．R．Statist．Soc．A，2006，169：805-827．

［34］于石成，廖加强，等．复杂抽样数据多水平模型分析方法及其应用．中国卫生统计，2014，31（2）：1-5．

［35］Carle AC．Fittingmultilevelmodels in complex survey data with design weights：Recommendations．BMCMedical Research Methodology，2009，9（1）：49．

（责任编辑：刘 壮）

国家自然科学基金（81202287）

1．哈尔滨医科大学卫生统计教研室（150081）

2．中国疾病预防控制中心慢性非传染性疾病预防控制中心

△通信作者：李镒冲，E-mail：alexleeliyichong＠gmail．com；刘艳，E-mail：liuyan＠ems．hrbmu．edu．cn