基于最大功效检验判断散落数据的归属*

中山大学公共卫生学院医学统计与流行病学系（510080） 赵 志 张晋昕

基于最大功效检验判断散落数据的归属*

中山大学公共卫生学院医学统计与流行病学系（510080） 赵 志 张晋昕△

目的给出医学研究中进行资料汇总时判断散落资料归属的方法。方法按照最大功效检验的思想，从Neyman-Pearson引理出发，推导出遗漏资料归属假设检验的拒绝域，据以得出判断结果的P值，全部计算在SAS环境中实现。结果此处给出的方法在分析文中的实例时，检验功效为0．9956，获得的归属判断结果甚为可靠。结论实际工作中出现一份资料从总体中散落，不宜直接通过差异性假设检验判别其归属，需用此处给出的假设检验方法合理地进行归并。

资料归属 Neyman-Pearson引理 最大功效检验

在临床试验［1－2］、社会调查［3］等研究实践中，录入数据资料时，有时会出现遗漏的情况。例如整理两组人群资料，对A、B两组资料分批录入。但是随后发现遗漏的部分资料还未录入，而此时已经难以分辨出这部分资料属于A、B两组中的哪一组，仅仅知道的是，这些遗漏的资料同属于A组或同属于B组。

试图将这些资料归并回所属组别，一种比较容易想到的做法是：根据所研究的指标，将那些遗漏的资料数据分别与两组资料数据进行t检验，得到两个P值，设其中只有一个P＞0．05，另一个P＜0．05，于是自然地将资料归为没有统计学意义（P＞0．05）的那组。但是，当研究的两组人群指标差异不是很大时，两次检验都会没有统计学意义；或者当两组人群指标差异大，两次t检验都得出P＜0．05的结果。此时，若是直接比较两个P值，将遗漏的资料归为P值较大的那组，其判断结果并不能令人信服。按照统计学假设检验的思维，为了较好控制决策所犯错误的大小，应通过一次假设检验推断出结论。Neyman-Pearson引理为解决此问题提供了思路。

最大功效检验［4］

在进行假设检验时，无论是决定接受还是拒绝原假设，研究者都可能犯错误。通常，要用犯错误的概率来评价和比较假设检验方法的优劣。也就是如何控制这些犯错误的概率，使得在某些情况下，所选检验具有最小的犯错误概率。

一般的做法是控制犯Ⅰ类错误的概率，例如水平为α的检验对所有可能的待检验参数θ∈Θ0，允许犯Ⅰ类错误的概率至多为α。在这样的一类检验中，一个好的检验犯Ⅱ类错误的概率也应当小，即当θ∈Θc0时它的功效比较大。如果一个检验犯Ⅱ类错误的概率比这类检验中所有其他检验都小，它理应是这个类中首选的检验。这便是最大功效检验（most powerful test，简称MP检验）。

对于一个需要进行假设检验的实际问题，想要得到最大功效检验并不容易。下面的定理清楚地描述了原假设和备择假设都只含一个关于样本的概率分布（即H0和H1都是简单假设）的情况下，如何得到一个MP检验。

定理（Neyman-Pearson引理）考虑检验H0：θ＝θ0对H1：θ＝θ1，对于一个样本x＝（x1，x2，…，xn），相应于θi的联合概率密度函数或概率质量函数是f（x｜θi），i＝0，1，利用一个拒绝域为R的检验，R满足对某个k≥0

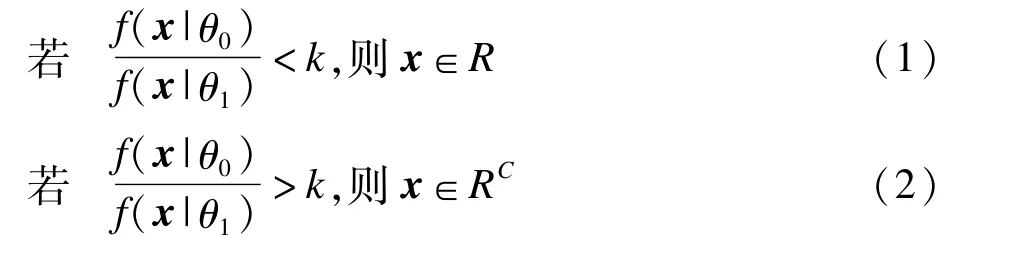
而且

则满足以上条件的检验是一个MP检验。

遗漏数据的假设检验实施

针对两组人群遗漏资料的归类，通过Neyman-Pearson引理做出的检验是很直观的：假设研究者关心的统计指标是均值，则判别遗漏数据归属时，可以借助遗漏部分算出的均值与两组总体均值的关系来推断。建立假设时，可以直接将H0和H1分别设为：遗漏数据所对应的总体均值等于A组的总体均值以及等于B组的总体均值。这样的检验结果要么是拒绝原假设，即遗漏数据来源于B组；要么不能够拒绝原假设，即没有充分理由否定遗漏数据来源于A组。此时，一定能给出一个判别的结果。而且，通过Neyman-Pearson引理得到的检验还是最大功效的检验，保证了判别结果的可靠性。

将所要研究的问题抽象出来：现有两组A、B服从正态分布的独立样本资料m份和n份

其中，u1－α为标准正态分布的1－α分位数。因此，得到水平为α下MP检验的拒绝域为

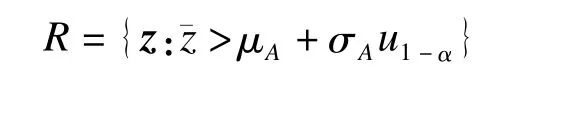
（2）当a＞0，即σ2A＜σ2B时，由式（6）得

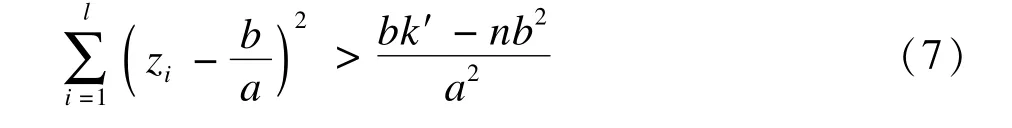
这里需要注意的是，在代入数据计算时，需要将遗漏的数据与A组数据合并后求μA和这是由于以上推导出来的拒绝域是在原假设H0成立的条件下得到的。也就是说，此时，遗漏的资料来自A组已被视作计算的前提。

举 例

某一次调查拟了解两个民族的肺活量水平。A、B民族的肺活量数据如表1所示。研究结束后，发现有12份调查表资料未被录入数据库，肺活量数据为2．65，2．78，2．79，2．85，2．88，3．14，2．98，2．99，3．05，3．08，3．15，3．22。可以确知的是这12名个体属于同一民族，可否根据统计学知识判断他们属于哪一个民族？

表1 两个民族人群的肺活量／L

由以上数据计算得到：

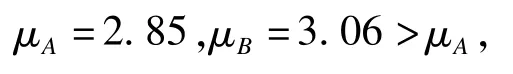
按照本文“遗漏数据的假设检验实施”第（2）部分内容建立假设并求得

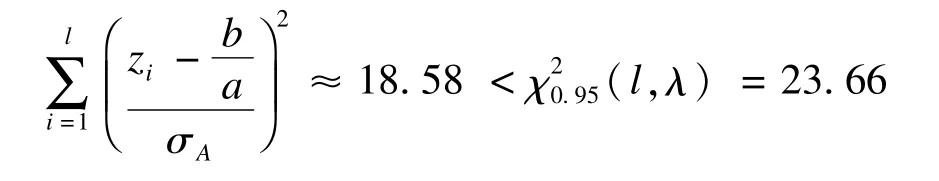
进一步通过SAS程序（见附录）得到检验的P值为0．17，也就是说，在显著性水平α＝0．05时，不能够拒绝原假设，即遗漏资料属于A民族。同时，可以计算出检验功效为0．9956，提示结论较可靠。

讨 论

实际调查研究中，简单的两组人群资料独立录入结束后，遗漏的部分可以通过数理统计中的Neyman-Pearson引理将其合理地判给所属的资料组别。并且，由于对应的检验是MP检验，故能够在控制Ⅰ类错误的前提下，使得犯Ⅱ类错误的概率最小，为实际工作判别资料的归属提供了切实有效的方法。

另外，如果出现多组资料录入后，遗漏了部分资料，本文所述方法尚不能够奏效。此时可以尝试通过判别分析或者其他一些算法分类器，如朴素贝叶斯（naive Bayes classifier）、支持向量机（support vector machines）等判断资料的归属情况，但是这些方法都不能像假设检验那样，在作出决策的同时控制犯错误的概率水平。

［1］O′Leary E，Seow H，Julian J，et al．Data collection in cancer clinical trials：Too much of a good thing．Clinical Trials，2013，10（4）：624-632．

［2］范彩霞，吴剑秋，寇莹莹，等．RDC Onsite-药物临床试验数据采集系统电子病例报告表常见疑问分析．药学与临床研究，2013，21（2）：196-198．

［3］陈向明．资料的归类和分析．社会科学战线，1999，4：223-229．

［4］Casella G，Berger R L．统计推断．第2版．张忠占，傅莺莺译．北京：机械工业出版社，2010，356-358．

［5］韦博成．参数统计教程．北京：高等教育出版社，2006，18-20．

附录 SAS假设检验P值和功效计算程序

（责任编辑：郭海强）

广东省高等教育教学改革重点项目（2013-113-11）

△通信作者：张晋昕，E-mail：zhjinx＠mail．sysu．edu．cn