基于随机森林回归的网络构建方法及应用*
哈尔滨医科大学卫生统计学教研室(150086) 侯 艳 杨 凯 李 康
基于随机森林回归的网络构建方法及应用*
哈尔滨医科大学卫生统计学教研室(150086) 侯 艳 杨 凯 李 康△
目的探讨基于随机森林(RF)回归估计因果关系网络的效果。方法通过模拟实验设定因果关系网络,对数据标准化后,利用全条件RF回归对其进行估计并评价其准确性。另外将该方法用于卵巢癌基因表达谱数据,并对分析结果进行验证。结果模拟实验结果表明RF回归对于预先设定网络关系的识别能力明显优于贝叶斯网络方法。当选择合适的阈值时,随着样本含量的增加基于随机森林回归方法构建的网络准确性不断提高,但传统经典的贝叶斯方法效果基本保持不变;实例分析结果验证,基于RF回归方法能够得到与现有数据库的网络结构。结论应用基于RF回归方法估计的网络,能够在样本量较少的情况下得出准确度较高的网络。
调控网络 随机森林回归 贝叶斯网络
目前有多种方法对基因调控、蛋白互作及代谢通路等网络进行估计,例如通过计算变量间偏相关系数推断变量间的条件相关关系、基于概率的方法确定信息网络边[1]、基于图形理论和信息传递算法获得网络中的直接信息流[2-3]、利用因果推断模型来获取变量的相关关系,如贝叶斯网络模型[4]等。当前的一些研究显示,贝叶斯方法可能是揭示复杂的细胞调控网络的最有效方法[5]。然而,贝叶斯方法使用的变量不能过多,且局限于低阶交互作用,因此在实际应用过程中受到一定的限制。本文在简要介绍随机森林(RF)回归构建网络方法的基础上,通过模拟实验研究这种方法的适用性和特点,与普通的贝叶斯方法进行比较,最后给出应用实例。
原理与方法
1.基本思想
RF回归是一种推断网络结构的新算法[6],其基本思想是对网络随机向量Xnet中m个变量中每个变量做应变量,其余m-1个变量作为自变量做RF回归分析,在全条件下得到任意两变量之间连接的权重,排序后按照一定的阈值取连接的边和方向,推断出需要估计的网络。由于RF回归不会出现过拟合的问题,因此可以在高维情况下进行分析;同时RF回归对数据的分布和变量之间的关系不需要做出任何假定,能够挖掘出具有交互作用的变量和各种复杂的非线性关系[9]。
2.网络变量关联计算
网络变量关联可以用通过RF回归得到的变量重要性测量值(VIM)来衡量。基于树方法的变量重要性测量方法有多种,本文使用方差改变量法,即对回归树的每一个节点t,计算由变量分裂导致的输出变量方差的总减少量,定义为

n(t)表示到达节点t的样本量,Var(t)为应变量的样本方差;n(tL)和n(tR)分别表示由节点t分裂的两新节点的样本量,即有n(t)=n(tL)+n(tR);Var(tL)和Var(tR)为两新节点的样本方差。对于一棵树,一个变量的重要性可以通过用这个变量分裂的所有节点的I(·)值相加获得,RF回归变量Xk的重要性可以用b棵树I(·)的平均值进行衡量,用公式表示为
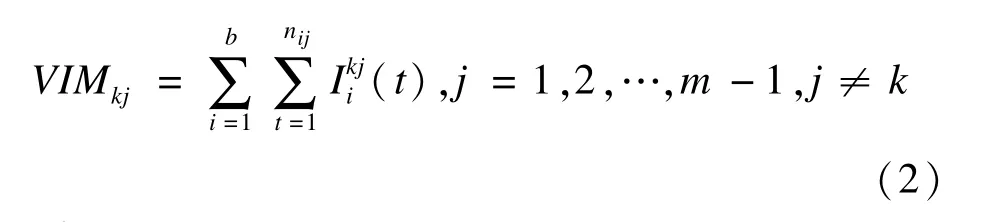
3.网络连接权重的计算
VIMkj表示在全自变量X-k条件下应变量Xk(k=1,2,…,m)与自变量Xj(j≠k)的关联度,因此两变量连接的权重wkj可以通过关联度VIMkj得到,即wkj=VIMkj。为了使m个不同RF回归模型中的VIM值具有可比性,需要预先对原始数据进行标准化,使所有变量有相等的方差,从而使从不同模型得到的权重具有可比性。对数据作m次RF回归,得到如下矩阵:

规定上式j=k时VIMkj=0,即对角线元素为零。
可以证明,在RF回归中所有变量重要性的总和等于因变量中被其解释的总方差,在未修剪树的情况下则通常非常接近因变量的总方差,可用公式表示为
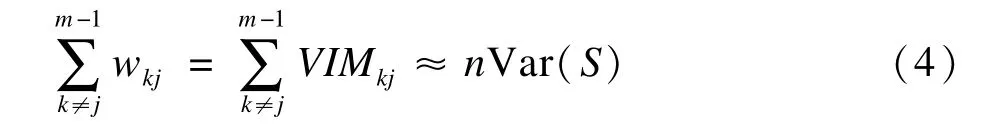
其中S是用来估计VIM值的样本数据。因此在数据标准化的情况下,不同RF回归模型的VIM值具有一定的可比性,从而可以对矩阵VIMkj所有的值排序,再通过设定的阈值c(VIM)(或通过确定连接的边数),取排序中{VIMkj≥c(VIM)}估计出网络连接的边和方向。如何给出合适的阈值是一个需要研究的问题。
上述算法实现可以使用random Forest R软件包。
模拟研究
1.无噪声情况的网络估计
(1)模拟实验目的和条件设置:研究网络变量之间存在线性关系及非线性相关关系时,基于RF方法构建相关网络的准确性,同时与经典的贝叶斯网络构建方法进行比较。实验设置15个变量和16条有向边(图1),选取的网络中包括:一个变量调控多个变量,如G12→{G14,G17};多个变量调控一个变量{G4,G9,G13}→G8,线性级联G11→G9→G10,前馈环路{G2,G3,G4}。
(2)网络参数及数据:变量之间的调控分别具有线性关系和交互关系,即{G13,G9}→G8和{G2,G4}→G3为交互作用,其他为线性调控关系。误差服从正态分布。样本量分别设为50、100、200、500和1000。
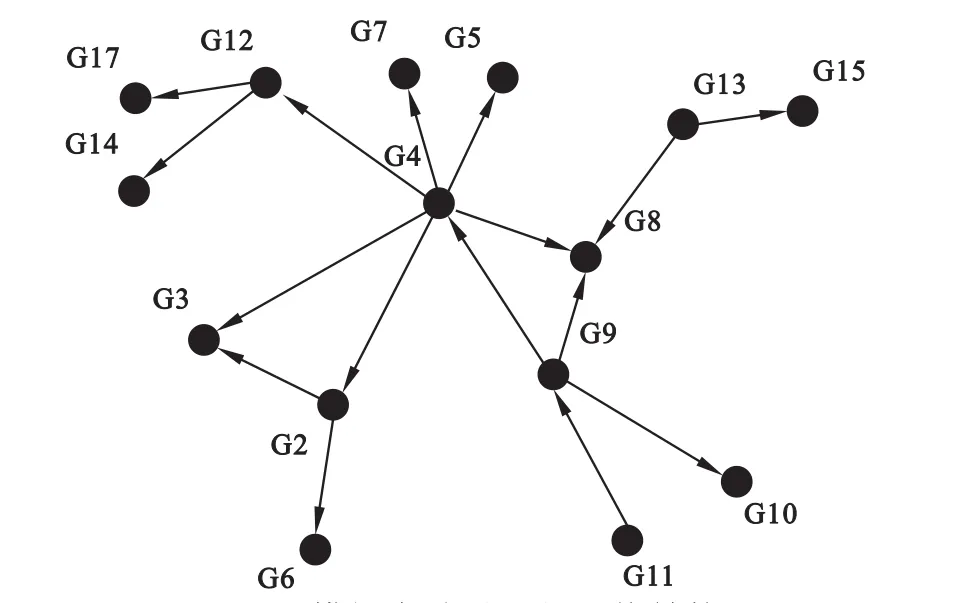
图1 模拟实验设置的网络结构
(3)网络数据模型:基于RF回归构建网络,分别设定VIM值为前15、20和25条边作为阳性边,剩余的边作为阴性边;对于贝叶斯网络,取结果为1的边作为阳性边,结果为0的边作为阴性边,分别使用AUC值及预测准确率(PRE)进行比较,对两种网络构建方法构建的网络进行评价。以上过程随机重复100次。
(4)模拟试验结果
表1模拟结果显示,当选择随机森林的边数(阈值)为15时(接近真实边的数目),在准确性评价中,AUC和PRE两项评价指标明显优于其他两种情况,同时明显优于贝叶斯方法;但是,当选定的边数(阈值)明显大于真实边数时(25条边),其准确性明显下降。当样本量小于200时,RF和贝叶斯建模的整体准确性不够稳定,在大于200时随样本量的增加趋于平缓(图2)。
2.具有噪声情况下的网络估计
模拟实验目的和条件设置:研究基于随机森林回归方法在网络变量间存在噪声变量时的识别能力,同时与不存在噪声变量的模拟数据分析效果进行比较。真实网络变量的条件设置同前,另加入200个服从正态分布的噪声变量。模拟随机重复100次。
模拟结果见图3。结果表明:利用随机森林回归估计网络的方法与不加入噪声变量的结果相近,即加入噪声变量后仍然能够很好地识别出变量之间的调控关系,并且保持较好的准确性。
3.阈值选择
上述两个模拟实验网络边数的选择,使用了选择15、20和25条边三种情况的VIM阈值。为了能够自动选择最合适的阈值,现使用随机置换的方法,在样本量为500例的情况下,打乱上述实验设置的15个变量的模拟数值(无噪声情况),使用随机森林回归计算相应的VIM值,进行100次置换。置换后所得到的VIM值可以得到随机情况下VIM值的分布,其99%分位数为0.1034,即选择阈值c(VIM)=0.1034。100次模拟数据中,变量调控关系大于阈值0.1034的平均有15条,这一结果与实验设置16条边的真实情况极为相近。由此可以得出,在实际应用中,在不知道真实调控关系的数量时,可以通过随机置换的方法估计真实调控关系的数量。需要注意的是,置换检验阈值的选择,可根据具体情况决定,如果需要控制“边”的数量,可选择比较严格的标准(如P99);若想适当放宽选入边的数量,则可以选择P95作为阈值。
表1 基于随机森林回归网络构建方法与贝叶斯网络对网络的识别效果(±S)

表1 基于随机森林回归网络构建方法与贝叶斯网络对网络的识别效果(±S)
评价指标样本量随机森林网络构建方法15条边20条边25条边贝叶斯网络AUC 50 0.760±0.058 0.727±0.048 0.705±0.038 0.745±0.045 100 0.838±0.048 0.801±0.036 0.757±0.025 0.800±0.033 200 0.896±0.034 0.839±0.027 0.782±0.017 0.829±0.034 500 0.945±0.022 0.865±0.016 0.792±0.012 0.842±0.027 1000 0.952±0.017 0.868±0.013 0.795±0.009 0.852±0.023 PRE 50 0.583±0.104 0.508±0.082 0.454±0.062 0.520±0.087 100 0.715±0.086 0.624±0.063 0.529±0.045 0.626±0.065 200 0.816±0.062 0.687±0.048 0.570±0.032 0.681±0.067 500 0.902±0.043 0.731±0.030 0.594±0.027 0.705±0.053 1000 0.916±0.034 0.744±0.029 0.612±0.025 0.724±0.045
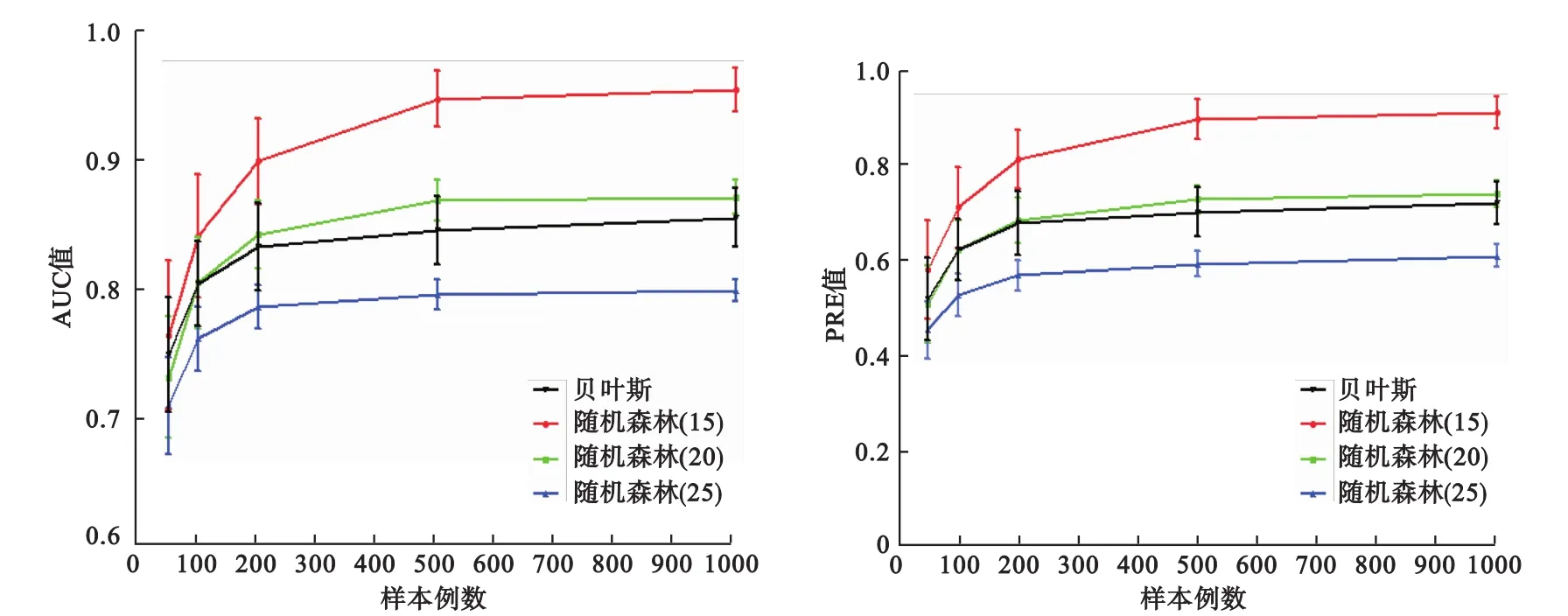
图2 基于随机森林回归网络构建方法与贝叶斯网络估计网络的准确性

图3 基于随机森林回归的网络构建方法抗噪能力情况
实例分析
数据来源:通过TCGA数据库下载570例卵巢癌患者以及8例健康对照数据的基因表达谱数据[7],其中包含12042个基因的表达值。
为了简化分析过程,首先筛选出与卵巢癌相关的基因,再对这部分基因构建网络。本研究使用基于W ilcoxon秩和检验的置换检验,进行1000次置换,筛选出P<0.05(校正后)的基因一共744个,通过对这部分基因进行KEGG通路富集分析,结果有12个基因显著富集在p53信号通路中。通过置换检验方法,100次随机置换后的VIM值的99%分位数为0.1157。确定边数选择的阈值c(VIM)=0.1157,获得16条可能具有调控关系的边,网络如图4所示。
进而,通过查询已有的基因/蛋白互作网络数据库GeneMANIA[8],发现这12个基因中,有9条边的因果关系出现在GeneMANIA的网络中(图5)。在这9条边中,基因CCNB1、CCNB2、CHEK1和CHEK2参与了比较多的调控,这个结果与随机森林回归所构建网络的结构相一致,说明这几个基因在p53信号通路中起到了很重要的作用。在剩余的7条边中,有4条边是与基因GTSE1(即PRKAR1A)有关,而在GeneMANIA中并没有相应的调控关系,提示这4条边需要进一步研究。
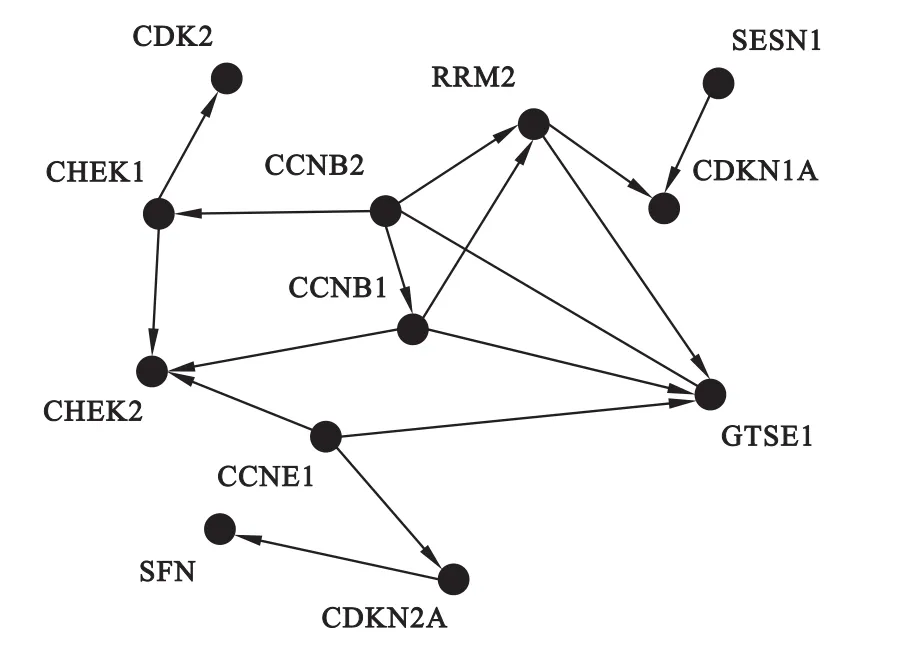
图4 卵巢癌患者p53信号通路中基因网络结构
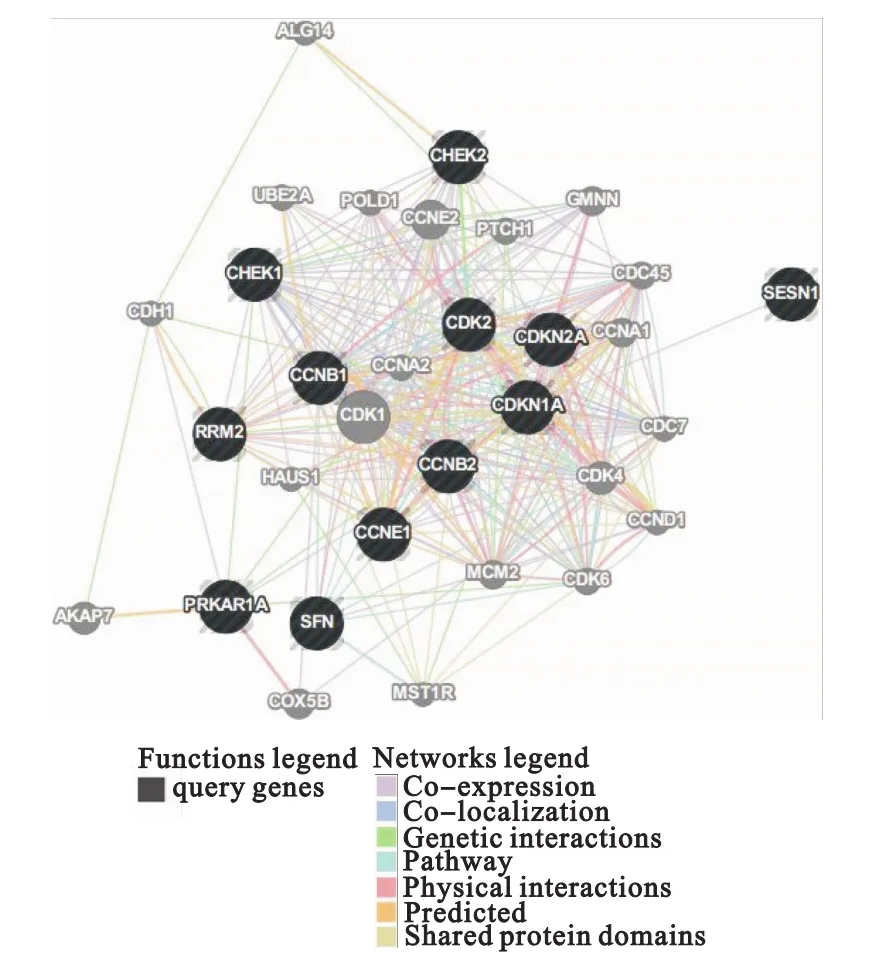
图5 12个基因在GeneMANIA中的网络关系
讨 论
1.基于RF回归估计网络的方法,两变量连接的权重wkj主要是利用全自变量条件下标准化的VIMkj得到。实际中,基于树方法的变量重要性测量方法有多种,本文使用方差改变量法。另外,VIM值的计算还有随机置换法,这种方法与方差改变量法相比在理论上有一定的优势,但在实际应用中得到的结果可能相近,而且需要更多的计算。
2.理论上,RF回归估计网络对数据的分布和变量之间的关系不需要做出任何假定,能够挖掘出具有交互作用的变量和各种复杂的非线性关系;而贝叶斯网络模型更适合单调或线性的调控关系。贝叶斯模型的优点之一是能够给出调控关系的方向,但模拟实验表明RF回归估计网络方法同样能够给出调控的方向,其原理是对任一变量,在全自变量条件下,能够对其方差做出较多解释的变量最有可能是调控其变化的变量。相对而言,对于一个变量调控多个变量更容易识别,如图1中的G12→{G17,G14};而对于多个变量调控一个变量则相对容易判错方向,如{G4,G9,G13}→G8。
3.RF可以在高维(如m>500)情况下构建网络,因此可以用于组学(如基因组/蛋白组)研究。同时RF回归方法可以分析非线性复杂关系的网络,附加的模拟实验结果表明,在变量之间呈指数、多项式等关系时,使用这种方法仍能够获得理想的结果。另外,这种方法也可以很容易推广到时间序列数据的分析。
4.关于RF回归参数的设置,在随机森林中,生成每一棵分类树时,所应用的自助样本集从原始的训练样本集中随机选取,每一棵树所应用的变量也是从所有变量mall中随机选取,并用袋外数据来衡量回归的效果。随机森林中最重要的参数有两个,即建立回归树的个数ntree和建立每个节点所取的变量两数目ntry。理论上讲,ntree越大得到的回归森林越稳定,本文取ntree=1000;ntry的选取主要有和ntry=mall-1两种方法,因本文变量数目不是很大,取ntry=mall-1。
5.实例分析结果表明,网络中多数的连接边能够被识别出来,并且能够给出调控的方向。然而,需要注意的是,实际各种变量之间的关系可能有多种,如基因共表达、基因调控、代谢通路等,其中共表达为无方向性,而RF回归方法同样能够对此进行分析,如VIMij≈VIMji时其方向不明确。需要注意的是,对于断面数据得到的因果网络关系最终需要实验的方法加以证实。
[1]Butte AJ,Kohane IS.Mutual information relevance networks:functional genomic clustering using pairwise entropy measurements.Pac Symp Biocomput,2000,418-429.
[2]Pesch R,Lysenko A,Hindle M,et al.Graph-based sequence annotation using a data integration approach.Journal of integrative bioinformatics,2008,5:2
[3]Harley E,Bonner A,Goodman N.Uniform integration of genome mapping data using intersection graphs.Bioinformatics,2001,17(6):487-494.
[4]Mani S,Cooper G F.A Bayesian local causal discovery algorithm,2004:731-735.
[5]Margolin AA.ARACNE:an algorithm for the reconstruction of gene regulatory networks in a mammalian cellular context.BMC bioinformatics,2006,7(suppl.1):S7.
[6]Breiman.L.Random Forests.Machine learning,2001,45:5-32.
[7]Integratedgenom ic analyses of ovarian carcinoma.Nature,2011,474(7353):609-615.
[8]Warde-Farley D,Donaldson SL,Comes O,et al.The GeneMANIA prediction server:biological network integration for gene prioritization and predicting gene function.Nucleic Acids Res,2010,38(Web Server issue):W 214-220.
(责任编辑:郭海强)
Network Reconstruction with Random Forest Regression and its Application
Hou Yan,Yang Kai,Li Kang(DepartmentofHealthStatistics,SchoolofPublicHealth,HarbinMedicalUniversity(150086),Harbin)
ObjectiveTo investigate the performance of network reconstruction based on random forest regression.MethodsSimulation studies were performed to evaluate the accuracy for network reconstruction with standardized data and conditional random forest regression.ResultsSimulation studies demonstrated that the network reconstruction performance with random forest regression is better than thatwith Bayesian network.In particular,when the thresholds are selected appropriately,the performance for network reconstruction based on random forest regression could improve with the increase of sample size while the traditional Bayesian network w ill remain stable.Besides,we applied this approach to the realexample and achieved satisfactory performance.ConclusionThe proposed method in this paper could achieve satisfactory performance for network reconstruction in small sample size.
Regulatory network;Random forest regression;Bayesian network
国家自然科学基金(81473072);中国博士后面上项目(2015M571445)
△通信作者:李康,E-mail:likang@ems.hrbmn.edu.cn

