群体异质性研究的潜变量分析方法
李丽霞赵 丽周舒冬张 敏郜艳晖张岩波
群体异质性研究的潜变量分析方法
李丽霞1赵 丽2周舒冬1张 敏1郜艳晖1张岩波3
社会学、心理学、医学等研究领域常常关注群体的异质性,异质性有时是可观测的,有时则不可见。由可观测变量(也称显变量)定义的亚组,例如按照性别、血型等显变量分组,此时每个观测所属的组别已知,群体异质性可见,可采用多组比较的方法对数据进行分析。但有时基于多个社会人口等分组变量来解释数据的异质性是不可行或不充分的,常常会产生大量分组,导致结果解释比较困难。实际研究中有些异质性不能直接观测到,即引起人群异质性的变量或来源未知,每个观测属于哪个亚类是未知的,观测属于哪一个亚类需要从数据中推断[1]。
异质性在科学研究中普遍存在,现在很多预防和干预措施经常在没有考虑个体特征情况下实施,即没有考虑人群中存在的异质性,尤其是不可见的异质性。不同特征的亚组对干预措施可能有不同的反应,将一个大的异质性群体分为多个小的同质性人群,根据观测的反应模式找到风险高的个体,针对小的同质性人群实施不同的干预措施可以使效应最大化,有针对性地进行干预具有非常重要的现实意义[2]。
传统对不可见异质性的探讨主要采用系统聚类、动态聚类或等级聚类等方法,聚类分析属于非参数方法,应用时需定义观测间距离和类间距离,而距离的定义有多种方法,如最长距离法、最短距离法、类平均法等,选择距离计算的方法不同聚类结果可能有所不同,给使用者造成一定困扰。而且传统聚类分析要求资料是具有相同测量尺度的定量变量,类内方差相同等条件,该方法不能给出拟合统计量,结果不可重复,且与初始值有关,在实际应用时这些条件往往很难满足[3]。
近年来对不可见异质性的研究逐渐成为医学、社会学和心理学等领域的研究热点,一系列分类潜变量的统计模型逐渐受到学者的关注,该类模型通过分类潜变量(categorical latent variable)来探测不能直接观察到的异质性,找到具有相似性个体所属的潜在类别(latent class)实现分类。本文主要介绍潜在类别分析、潜在剖面分析、因子混合模型、增长曲线混合模型等潜变量分析方法。
潜在类别分析(latent class analysis,LCA)
LCA属于混合模型(m ixture modeling)的范畴,是一种以“个体”为中心的方法,传统的LCA要求基于分类的可测变量为分类变量,利用模型中的分类潜变量来解释人群中的异质性。该模型假设每个观测仅属于潜变量的c个类别中的某个类,通常需要满足局部独立性假设,即:给定潜变量的类别时显变量间相互独立,该假设意味着显变量间的相关完全由不可测量的分类潜变量来解释,显变量之间没有残差的协方差[4]。
假设有N个观测数据,则显变量的联合概率分布可表示为:
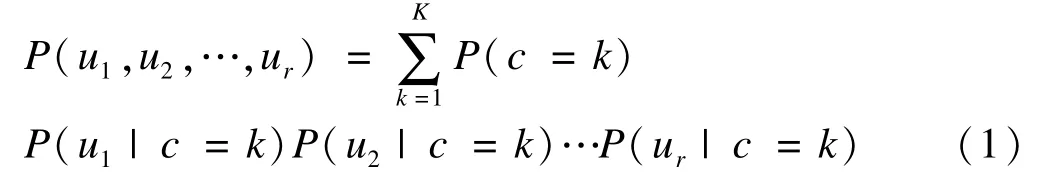
式(1)中,c为分类的潜变量,u1、u2、…ur为r维二分类显变量,P(c=k)为潜在类别概率,表示观测属于第k个类别的概率;P(ur|c=k)表示在类别k内显变量ur取值为某个水平的概率。当某观测的反应模式为u1,u2,…,ur时,可以据式(2)计算其属于某个类别的概率。

LCA中有两种参数:潜在类别概率和显变量的条件概率,潜在类别概率可描述群体在各个类别中的分布,显变量的条件概率表示潜变量的本质,类似于因子分析中的因子载荷,可反映显变量和潜变量间的关联,能使研究者识别潜在类别的结构,并根据它们来对潜在类别命名。
LCA利用一个或多个分类的潜在变量来解释多个外显分类变量之间的复杂关联,同时具有因子分析和聚类分析的功能,与传统聚类方法相比,LCA在概率基础上对人群进行分类,即个体以一定的概率归属于各个类别,最终将被分到后验概率最高的那个类别,类别数的选择标准不再主观,不需要人为选择分类的界值点,不需要变量满足正态分布,尤其可以处理非线性关系,具有分类客观、不受变量类型限制、无需标准化、同时可考虑协变量等优点。近年来协变量的引入、局部独立性假设的放松等方面的扩展拓宽了潜在类别模型应用的领域。国外将其广泛应用于教育与心理测验、社会心理调查、疾病诊断、人才测评等方面。例如,Muthen等利用17个二分类的测量反社会行为的题项将研究对象分为4类[5];Sutfin等学者根据大学生过去一个月吸烟量、吸烟的频数等指标使用LCA将大学生的吸烟者分为5大类[6];在临床心理学方面,Xian等人用LCA对戒烟复吸人群进行分类,并研究复吸类型与精神疾病的关系[7]。
潜在剖面分析(latent profile analysis,LPA)
与LCA一样,LPA假定潜变量为分类变量,不同之处在于LPA中可观测变量为连续性变量,在潜变量指定的不同类别下显变量的均值不同,同一类别内个体间具有较小的变异,表现为较强的同质性。
LPA满足两个基本假设:①在第k类潜在类别内,可测变量Y来自独立多元正态分布N(μk,∑k),∑k中协方差为0,类间方差可以相等,也可不等。②在潜变量条件下可测变量间相互独立,即满足局部独立性[8]。
LCA和LPA都可探测人群中是否存在异质性亚组,在不可见的异质性群体中,显变量间的关联可由其背后共同的一个分类潜变量来解释,与LCA一样,LPA在医学、心理、社会学等领域都有非常广泛的应用。例如Schmiege等依据某队列研究中2232例吸烟者的咳嗽、咳痰等6个呼吸道症状(按照严重程度记为1~6分)将吸烟者分为3个亚类,14%的个体属于高症状组,41%的个体为低症状组,研究发现45%的个体咳嗽、咳痰得分高,而其他症状轻微,定义为“气道清除症状组”,在临床工作中识别这个发病比例较高的群体并施加有效的干预有重要意义,研究者同时也探讨了性别、目前吸烟状况等协变量对分类的影响[9]。
实际应用时当出现拟合LCA或LPA模型效果差而拒绝该模型时意味着局部独立性假设不成立,此时可考虑以下替代方法:(1)放松局部独立性的要求,在模型中增加一个或多个直接效应参数来解释外显变量间的剩余关联;(2)当存在很多冗余变量时可在模型中去除1个或多个外显变量;(3)当群体异质性由多个维度构成时,可增加分类潜变量的数目,由多个分类潜变量支配显变量,从多维度对人群进行分类,并且可进一步探讨分类潜变量间的关联,有着重要的学术应用价值;(4)在每个亚类内引入连续型潜变量,即用类内因子来解释类内显变量的剩余相关,称为因子混合模型。
因子混合模型(factor m ixturemodeling,FMM)
传统的因子分析假设样本中的个体来自于同质的研究总体,模型中公因子F为连续性潜变量,解释可观测变量间的相关性,探讨潜在的构念。FMM可以探测研究总体存在不可见异质性的同时拟合潜在的因子结构,近年来成为研究的热点。
FMM属于横断面混合分析的一种,该模型中同时含有连续性潜变量和分类潜变量,是因子分析和潜在类别模型的混合体,具有这两种方法的优势。FMM中分类潜变量对观测进行分类的同时,连续性的因子解释类内的异质性,并且可以考虑测量误差[10]。
LCA/LPA中要求条件独立性,可测变量的相关完全被分类潜变量所解释,但可观测变量的相关不仅仅是由于类别的不同引起的,与LCA/LPA不同,FMM在每个亚类内显变量没有被假设为相互独立,类内的显变量被允许共变,类内的变异用连续性潜在因子解释,分类的潜变量拟合未观察到的总体的异质性,并通过潜在类别模型对观测进行分类。FMM主要关注点是找到异质性的亚类及类内的潜在因子,可观测变量的相关被分解为两部分:类别的不同,类内连续性因子不同。
假设含有k个潜在类别,显变量为y1、y2、…yp,则FMM可表示为:

对于某一个亚类k,yik是观测i的p维反应模式,υk是测量截距,Λk是p×m维因子载荷矩阵,ηik为m维因子得分向量,εik为p维残差向量,αk为m维因子均值向量,ζik为m维残差向量,服从均值为0,方差为ψ的正态分布,协变量引起的异质性也可以纳入模型中。
根据是否满足测量不变性(measurement invariance,MI)和所构建模型中连续性潜变量的分布形式,Muthen等人将FMM分成四个分支,见图1。其中c为分类的潜变量,f为连续性潜变量,y为可测变量。前两个分支(FMM-1、FMM-2)满足MI条件,强调因子分析方面;后两个分支(FMM-3、FMM-4)不满足MI,更强调模型在分类方面的作用。这里的测量不变性指异质性的亚类内因子载荷、截距、残差的方差是否相等[11]。
FMM-1也称为潜在类别因子分析模型(latent class factor analysis,LCFA),该模型中不同亚类内因子的均值不同,可测变量的截距、因子载荷均相等,因子的方差协方差矩阵为0,表明没有类内的异质性,图2(a)的因子分布图中,横坐标为4个亚类的4个因子得分,纵坐标为因子得分的频数。
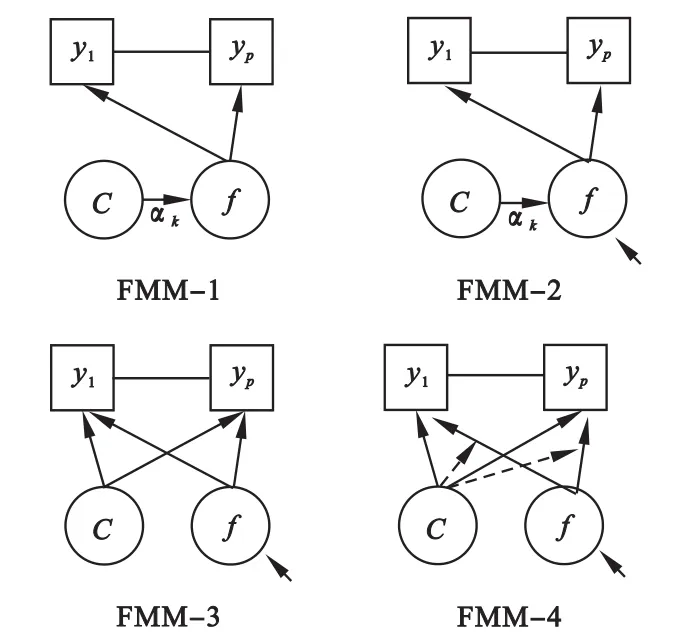
图1 FMM示意图

图2 (a) FMM-1中因子的分布
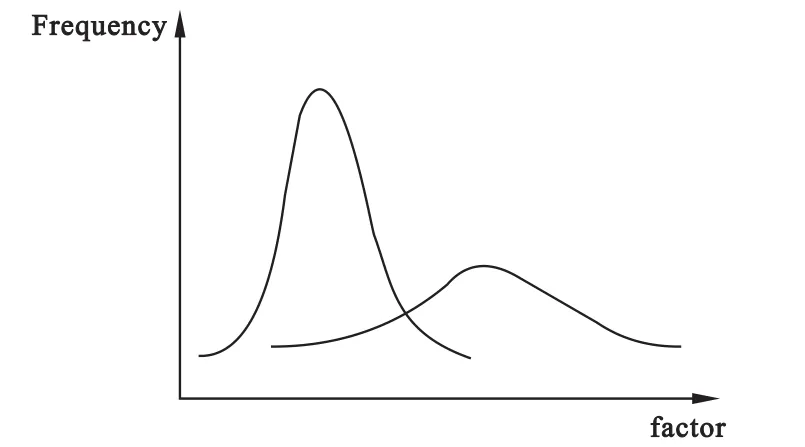
图2 (b) FMM-2中两个亚类的因子分布
FMM-2中不同的亚类有不同的因子均值αk,指向f的箭头表明c不能解释f的所有变异,仍存在不可解释的类内变异。图2(b)显示两个亚类中公因子的均值和方差均不相同[12]。
FMM-3和FMM-4中分类潜变量c直接指向可测变量,或c指向f到y的虚线表明不同亚类内测量参数、因子的方差等都不相同。
目前FMM在医学、心理学等学科都有比较成功的应用,例如,Clark等人将该模型成功用于行为障碍(conduct disorder,CD)的研究中,行为障碍的测量使用了13个二分类的题项,共调查了1786名儿童,研究者使用FMM-2模型拟合非正态分布的行为障碍因子时将受试对象分为两类:无CD症状类和CD症状类,对研究对象分类的同时估计两个亚类的行为障碍因子的得分均值和方差。Viroli等采用FMM对856例老年人进行认知评价,最终将人群分为正常人、认知功能损伤、老年痴呆症3类,同时识别出4个维度的连续性潜在因子[12-13]。
结构方程混合模型(structural equation m ixturemodel,SEMM)
SEMM是FMM的扩展,假设多变量分布是混合分布,对于某个潜在类别k,y服从正态分布N(μk,∑k),在每一个潜在亚类内构建潜在因子之间的回归关系,不同的潜在类别中变量间的复杂关系不同,即亚类中的测量参数和结构参数不同。这样既可以通过分类潜变量处理客观存在但没有观察到的异质性,处理数据不服从正态分布的情况,又可以分析连续潜变量间的关系[14]。其示意图见图3,ξ、η为连续性潜变量,c为分类潜变量,c指向ξ、η的箭头表明ξ的均值和η的截距在不同的亚类不同,c指向ξ到η的虚线表明不同亚类中ξ与η之间的回归系数不同[15]。拟合SEMMs时运算时间比较长,可能不收敛,可以先拟合限制较多的模型,然后逐步放松限制。
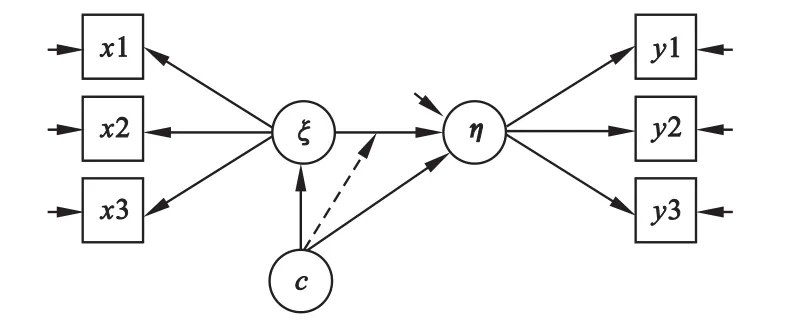
图3 SEMM示意图
SEMM在心理、社会、经济学等研究领域应用前景巨大,例如Jedidi等采用SEMM研究消费者对某新食品喜好的影响因素,结果显示:研究总体中存在两个不可观测的亚类:一类人群主要重视愉悦感,另一类则重视健康,两个不同亚类中两个知觉维度“甜味程度”和“口味的丰富感”对食品的喜好的影响是不同的(甜味程度、口味丰富感分别被两个可观测的显变量测量)[16]。
增长混合模型(Grow th m ixturemodel,GMM)
传统的增长曲线模型假设观测来自同一个总体,因此拟合简单的增长轨迹就能很好的反映指标的变化趋势,每个观测的增长轨迹围绕平均增长轨迹变动,而且假设影响增长因子的协变量以相同的方式影响每一个观测。但很多情况下大样本数据是存在异质性的,GMM是近年来出现的探测增长轨迹异质性的一种新的纵向数据分析技术,可以帮助研究者探讨总体中是否存在增长轨迹不同的潜在亚组,容许不同亚组增长曲线的截距、斜率因子及其方差不同,且协变量对它们的影响也可以不同,这一点通过模型中的分类潜变量来实现,1999年Muthen等学者提出GMM模型,见式(4)。

其中Yt为重复观测的结果变量,ηk0为截距增长因子,ηk1为斜率因子,εkt为测量误差,k为不可观测的亚组,αk0为第k类的截距因子的均值,αk1为第k类的斜率因子的均值,ζk0、ζk1分别为截距、斜率因子的残差[17]。图4为GMM示意图,c表示潜在的分类变量。
假设同一亚类的所有观测是同质的,不存在变异,即每个潜在类别的增长因子的方差估计值为0,称其为潜在类别增长曲线模型(latent class grow th analysis,LCGA),它是GMM模型的特例,在拟合GMM模型以前,研究者可以先拟合LCGA,探测数据是否存在不可观测的亚类,此时模型也比较容易收敛[18]。对GMM模型扩展,考虑协变量和结局变量,见图5,称其为一般增长混合模型(general grow th mixture modeling,GGMM)。
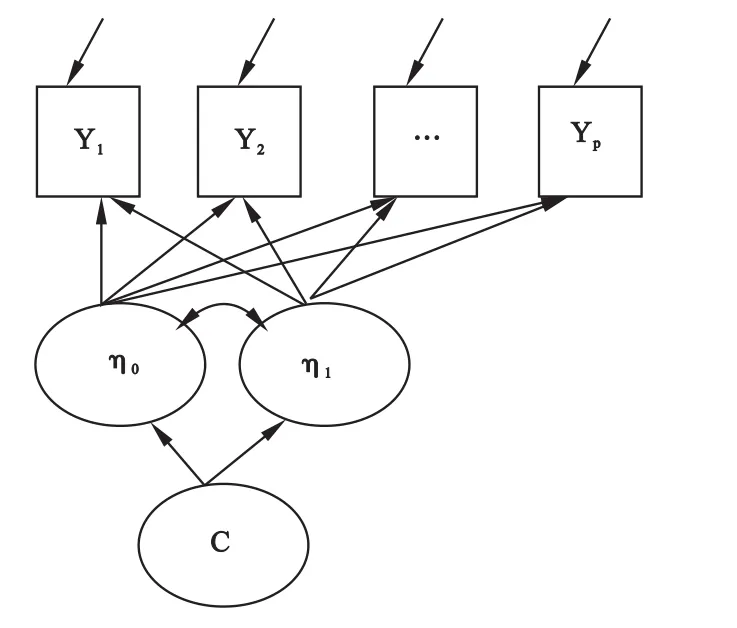
图4 GMM示意图

图5 GGMM示意图
Muthen等采用GMM对美国公立学校7~10年级3102个学生4年的数学成绩的随访资料进行分析,同时研究性别、种族、母亲教育程度、学生有无辍学想法等协变量对增长轨迹的影响,结果发现存在3个潜在亚类,20%的学生数学成绩的增长较差,28%属于中等情况,52%的比较好,并在模型中加入了辍学与否这个结局变量,构建GGMM模型探讨协变量、增长轨迹对辍学的影响,研究结果对于帮助教育工作者找到辍学的高风险人群以早期施加干预具有重要的意义[17]。Walsh等对210例有高风险性行为的男性给予干预措施后随访12个月,构建GMM模型识别出两个亚类增长轨迹不同,46%的受试对象(风险减少组)在干预措施后,无保护的性行为次数减少,而54%的受试者(风险持续组)在干预后仍然持续有高频率的无保护性行为,为进一步研究风险持续组的受试对象的特征并施加相应的干预提供依据[19]。
潜在转换分析(latent transition analysis,LTA)
LTA是潜在类别模型的纵向扩展,模型中含有两个或以上的潜在分类变量,容许观测随着时间的变化在两个分类的潜在类别变量的类别间转换,见图6,C1为t时间点的潜在分类,C2为t+1时间点的潜在分类变量。在LTA中亚组称为“潜在的状态”(latent statuses),模型中有三种参数被估计:(1)在不同的时间点,观测属于某一个亚类的概率;(2)转换概率:观测从t时间点时的状态转为t+1时间点时另一个状态的概率;(3)项目反应概率:类似因子分析中的因子载荷。LTA可以进行多组分析,其扩展模型可以包含协变量和结局变量,对模型的详细描述见相关文献[20]。

图6 LTA示意图
上述含有分类潜变量的模型都可看成有限混合模型的亚类,目前有限混合模型是探索研究总体中是否存在不可见异质性的广泛使用的数据分析技术,其主要作用是找到有相似反应模式或增长轨迹的有意义亚组。LCA、LPA、FMM和SEMM属于横断面混合模型,GMM、LTA属于纵向混合模型,LPA和LCA仅包含一个分类潜变量,而FMM、GMM则包含一个分类潜变量和一个或多个连续型的潜变量,见表1。

表1 常见的混合模型特点
以上模型的参数估计方法有多种,常用的有EM算法和牛顿—拉普森法,其中EM算法目前被广泛地应用,其优点是不受初始值选择的影响,具有稳健性,缺点是迭代次数较多,且不提供标准误的估计。Ver-munt建议将EM和NR算法结合使用,这样同时兼顾了EM算法的稳健性和NR算法速度快的优点。混合分布经常存在多个局部最大值,当潜在亚类比较多时,往往会遇到不收敛的问题,可以重复多个随机的初始值。Monte Carlo模拟研究也表明样本量、参数个数、潜在类的分离程度等都对模型的拟合结果有影响。
混合模型应用中最关键的问题是解决如何确定研究总体中包含的不可观测的亚组数,即是否真的存在潜在的类别,Bauer等警告亚组的存在可能仅仅是因为数据呈偏态或非正态分布导致,每一个亚组并没有实际意义,可能会产生过度提取亚类的情况[21]。潜在类别数的确定对于结果解释和统计推断至关重要,一般采用AIC、BIC、aBIC等信息统计量指标对模型进行评价,许多模拟研究表明BIC是比较好的模型选择指标(BIC取值越小表明所选模型较优)。2001年Lo,Mendell,Rubin等学者提出了基于似然比为基础的比较类和类模型的Lo-Mendell-Rubin似然比检验(LMR LRT),值小表明含类的模型较优。2002年Muthen等人提出SK检验(skewness and kurtosis test)作为LMR LRT的一个补充。Bootstrap似然比检验(BLRT)也是目前用的比较多的一个方法,值小表明含类的模型较优。模型的分类质量可通过熵(Entropy)进行评价,取值在0到1之间,越接近1表明分类越明确。模型的选择同时要结合理论知识、前人的研究结果及其它的辅助信息,最终的目的是选择最佳模型,捕捉到有实际意义的亚组。
近年来由于计算机技术的快速发展,分类潜变量模型的应用变得越来越广泛,但目前国内使用FMM、GMM等分类潜变量模型探讨数据异质性的应用尚未见报道,本文旨在通过对该类方法的介绍推动其在实际数据分析中的应用,为分类潜变量方法在研究工作中的正确选择和应用提供有意义的参考和指引。
[1]M cLachlan GJ,Chang SU.M ixture modelling for cluster analysis.Stat Methods Med Res,2004,13(5):347-361.
[2]Muthen B,Brown CH,Masyn K,et al,General grow th m ixturemodeling for random ized preventive interventions.Biostatistics,2002,3(4):459-475.
[3]Magidson J,Vermunt JK.Latent classmodels for clustering:A comparison with K-means.Canadian Journal of Marketing Research,2002,20(1):36-43.
[4]Hagenaars JA,M ccutcheon AL.Applied latent class analysis.New York:Cambridge University Press,2002:56-213.
[5]Muthen B.Statistical and substantive checking in grow th m ixture modeling:comment on Bauer and Curran.Psychol Methods,2003,8(3):369-377.
[6]Sutfin EL,Reboussin BA,M cCoy TP,et al.Are college student smokers really a homogeneous group?A latent class analysis of college student smokers.Nicotine Tob Res,2009,11(4):444-454.
[7]Xian H,Scherrer JF,Madden PA,etal.Latent class typology of nicotine withdrawal:genetic contributions and association with failed smoking cessation and psychiatric disorders.Psychol Med,2005,35(3):409-419.
[8]M clachlan G,Peel D.Finite m ixture models.New York:W iley,2000:66-345.
[9]Schm iege SJ,Meek P,Bryan AD,et al.Latent variablem ixturemodeling:a flexible statistical approach for identifying and classifying heterogeneity.Nurs Res,2012,61(3):204-212.
[10]Lubke GH,Muthen B.Investigating population heterogeneity with factorm ixturemodels.Psycholmethods,2005,10(1):21-39.
[11]Muthen B.O.Beyond SEM:general latent variablemodeling.Behaviormetrika,2002,29(1),81-117.
[12]Clark SL,Muthen B,Kaprio J,et al.Models and strategies for factor m ixture analysis:an example concerning the structure underlying psychological disorders.Struct Equ Modeling,2013,20(4):681-703.
[13]ViroliC.Using factorm ixture analysis tomodel heterogeneity,cognitive structure,and determ inants of dementia:an application to the aging,demographics,and memory study.Stat Med,2012,31(19):2110-2122.
[14]Lubke G,Tueller S.Evaluation of structural equation m ixturemodels parameter estimates and correct class assignment.Struct Equ Modeling,2010,17(2):156-192.
[15]Muthén,L.K,Muthén,B.O.Mplus Version 5.0 User's Guide.Los Angeles,CA:Muthen and Muthen,2007:131-185.
[16]Jedidi K,Japal HS,Desarbo WS.Finite-mixture structural equation models for response-based segmentation and unobserved heterogeneity.Marketing Science,1997,16(1):39-59.
[17]Muthen B,Muthen LK.Integrating person-centered and variable-centered analyses:grow th m ixture modeling with latent trajectory classes.Alcohol Clin Exp Res,2000,24(6):882-891.
[18]Ram N,Grimm KJ.Grow th mixturemodeling:a method for identifying differencesin longitudinal change among unobserved groups.Int JBehav Dev,2009,33(6):565-576.
[19]Walsh JL,Senn TE,Scott-Sheldon Lori AJ,et al.Using grow th mixturemodeling to identify heterosexualmen who reduce their frequency of unprotected sex following a behavioral intervention.AIDS Behav,2012,16(6):1501-1510.
[20]Lanza1 ST,Patrick ME,Maggs JL.Latent transition analysis:benefits of a latent variable approach tomodeling transitions in substance use.JDrug Issues,2010,40(1):93-120.
[21]Bauer DJ,Curran PJ.The integration of continuous and discrete latent variablemodels:potential problems and promising opportunities.Psychol Methods,2004,9(1):3-29.
(责任编辑:郭海强)
广东省科技厅社会发展领域科技计划项目(2013B021800269);国家自然科学基金(30972553)
1.广东药学院公共卫生学院卫生统计学教研室,广东省分子流行病学重点实验室
2.普瑞盛医药科技开发有限公司
3.山西医科大学公共卫生学院卫生统计学教研室

