完全随机缺失条件下连续型随机变量数据缺失插补方法的比较研究

中国医学科学院基础医学研究所，北京协和医学院基础学院流行病学与卫生统计学系（100005）

张 彪 韩 伟 庞海玉 薛 芳 厚 磊 王子兴 王钰嫣 姜晶梅△

完全随机缺失条件下连续型随机变量数据缺失插补方法的比较研究

中国医学科学院基础医学研究所，北京协和医学院基础学院流行病学与卫生统计学系（100005）

张 彪 韩 伟 庞海玉 薛 芳 厚 磊 王子兴 王钰嫣 姜晶梅△

目的探讨完全随机缺失条件下连续型随机变量数据缺失对研究结果的影响，对各方法插补效果进行比较。方法基于上海地区35岁及以上吸烟人群吸烟与肺癌死亡关系的完整数据集，在5%、10%、20%及30%缺失率下，模拟单变量（吸烟年数sy）缺失，采用了7种方法处理单变量缺失；模拟多变量（吸烟年数sy和每天吸烟支数smd）缺失，采用了4种方法处理多变量缺失。对插补效果从缺失变量均值的变化、插补精确性及插补后模型参数的变化三个方面进行评价。结果单变量缺失：各缺失率下，回归插补sy均值的偏差最小，MI／REG、MI／PMM和MI／MCMC插补后模型参数的偏差均较小，删除法sy均值与模型参数的偏差均最大。多变量缺失：各缺失率下，回归插补sy均值的偏差最小，删除法最大；条件均值插补smd均值的偏差最小，MI／MCMC最大；条件均值插补模型参数的偏差最小，MI／MCMC最大。结论用不同指标对各方法插补效果进行评价会得出不同的结果，应根据统计分析的目的和关注点选择最合适的缺失数据处理方法。总体来看，插补法处理缺失数据的效果优于删除法，缺失率越高，优势越显著。

缺失数据 多重插补

在医学研究中，数据缺失是一个普遍存在的问题［1］。数据缺失会导致样本信息减少和统计检验效能降低，降低研究结果的有效性［2］，增加统计分析的复杂性［3－4］。对缺失数据插补是国内外常用的缺失数据处理方法，完全随机缺失是各插补方法最理想的应用环境，并且从理论上讲，完全随机缺失条件下的参数估计是无偏的，即完全随机缺失是可忽略的缺失，但在一次具体研究中是否真的可以忽略完全随机缺失值得探讨。本研究基于完整数据集模拟完全随机缺失数据集，探讨连续型随机变量数据缺失对研究结果的影响，采用不同方法插补缺失数据，并对插补效果进行比较及评价。

资料与方法

1．数据来源 研究数据源于1989－1991年开展的“中国吸烟与全死因关系”横断面调查，选取上海地区35岁及以上吸烟人群吸烟与肺癌死亡关系的数据进行插补方法研究，共14911条完整观测。

2．研究涉及的变量 详见表1。

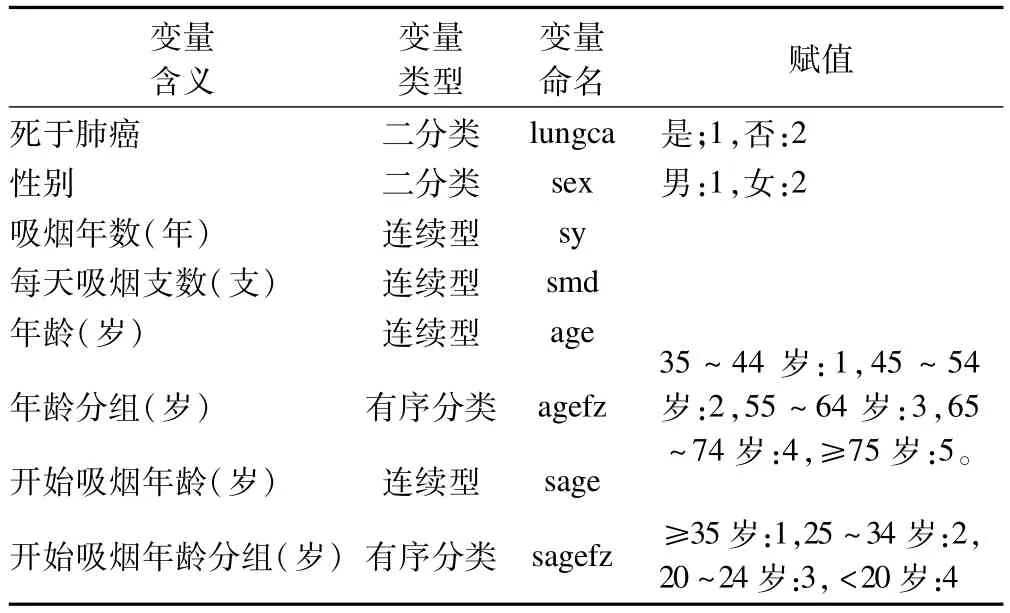
表1 研究涉及变量情况

3．不完整数据集的构建 基于完整数据集模拟完全随机缺失的不完整数据集。

（1）单变量缺失：模拟sy缺失的不完整数据集，在5%、10%、20%和30%的缺失率下各模拟100次。

（2）多变量缺失（任意缺失模式）：模拟sy与smd均缺失的不完整数据集，缺失观测中仅sy缺失占30%，仅smd缺失占20%，两者均缺失占50%（该比例分布基于原始调查数据集实际缺失情况），缺失率及模拟次数与单变量缺失相同。

4．插补方法及效果评价

单变量缺失：采用七种方法处理缺失值［5－8］，①删除法：删除sy缺失的观测。②条件均值插补：按sex、agefz和sagefz将数据交叉分组分为20组。计算各组中sy的均值，将组均值作为该组中缺失项的插补值。③回归插补：以sy为因变量，sex、age及sage为协变量建立回归方程，用回归预测值作为缺失数据的插补值。④多重插补-趋势得分法（MI／PS）：按照sex分层，每层中以sy缺失指示变量R（R＝1，缺失；R＝0，未缺失）为因变量，age、sage为协变量建立logistic回归方程，sy缺失的概率为趋势得分，基于趋势得分将观测分为20组，在每组中应用近似贝叶斯Bootstrap方法分别对缺失值进行3次、5次和10次插补。⑤多重插补-回归法（MI／REG）：以sy为因变量，sex、age和sage为协变量建立回归方程，分别对缺失值进行3次、5次和10次插补。⑥多重插补-预测均数匹配法（MI／PMM）：以sy为因变量，sex、age和sage为协变量建立回归模型，选取与缺失数据的预测值最接近的5个真实值，从中抽样对缺失数据进行3次、5次和10次插补。⑦多重插补-马尔科夫蒙特卡洛法（MI／MCMC）：按sex分层，每层中采用sy、age和sage建立马尔科夫链对缺失数据进行3次、5次和10次插补。

多变量缺失：采用四种方法处理缺失值［5－8］，①删除法：删除sy或smd缺失的观测。②条件均值插补：按sex、agefz及sagefz组将全部观测分为20组，以每组中sy和smd的均值来插补相应的缺失值。③回归插补：以sex、age和sage为协变量，分别以sy及smd为因变量建立回归模型，插补缺失值。④MI／MCMC：按sex分层，每层中采用sy、age、sage和smd建立马尔科夫链，对缺失数据进行3次、5次和10次插补。

对各方法的插补效果从以下三方面进行评价：

（1）插补后缺失变量均值的改变［9］：计算插补后缺失变量均值的绝对偏差和均值的相对偏差其中为缺失变量插补后的均值，μ为真实的均值。再计算100次模拟的MAD及MRD的均数，即为均值的平均绝对偏差MADM及平均相对偏差MRDM，MADM和MRDM越小插补效果越好。

（2）插补的精确性［9－11］：计算插补值的平均绝对偏差MADD和平均相对偏差MRDD，插补的均方误平方根RMSE，插补方差占总方差的百分比PMSE。

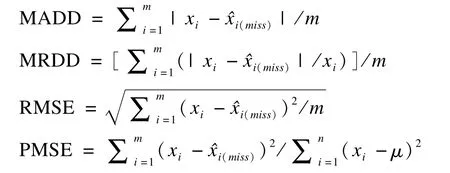
（3）插补后模型参数的改变［12－13］：采用logistic回归模型分析lungca（因变量）与sex、sy和smd的关系。将插补数据集的模型参数估计结果与完整数据集的结果相比较，计算模型参数的平均绝对偏差MADP和平均相对偏差MRDP。

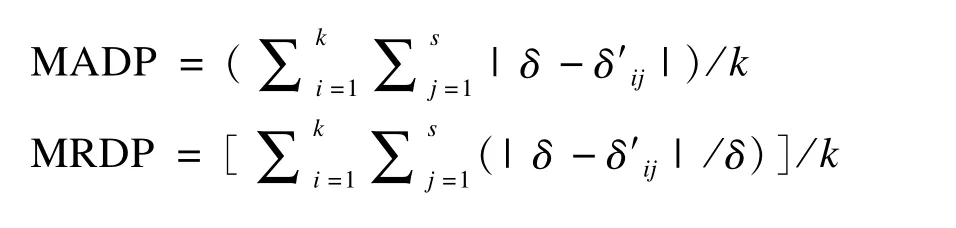
其中，k为重复模拟次数，s为模型中估计的参数个数，δ为完整数据集的参数估计值，δ′ij为插补数据集的参数估计值。MADP和MRDP越小插补效果越好。

结 果

1．单变量缺失

表2及表3显示了5%缺失率下各法插补后sy均值及模型参数的改变。sy均值的偏差由大到小为：删除法＞MI／PS＞MI／PMM＞MI／REG＞条件均值法＞MI／MCMC＞回归插补法；插补精确性由高到低为：回归插补法＞MI／PMM＞条件均值法＞MI／MCMC＞MI／REG＞MI／PS；模型参数偏差由高到低依次为：删除法＞MI／PS＞回归插补法＞条件均值法＞MI／PMM＞MI／MCMC＞MI／REG。

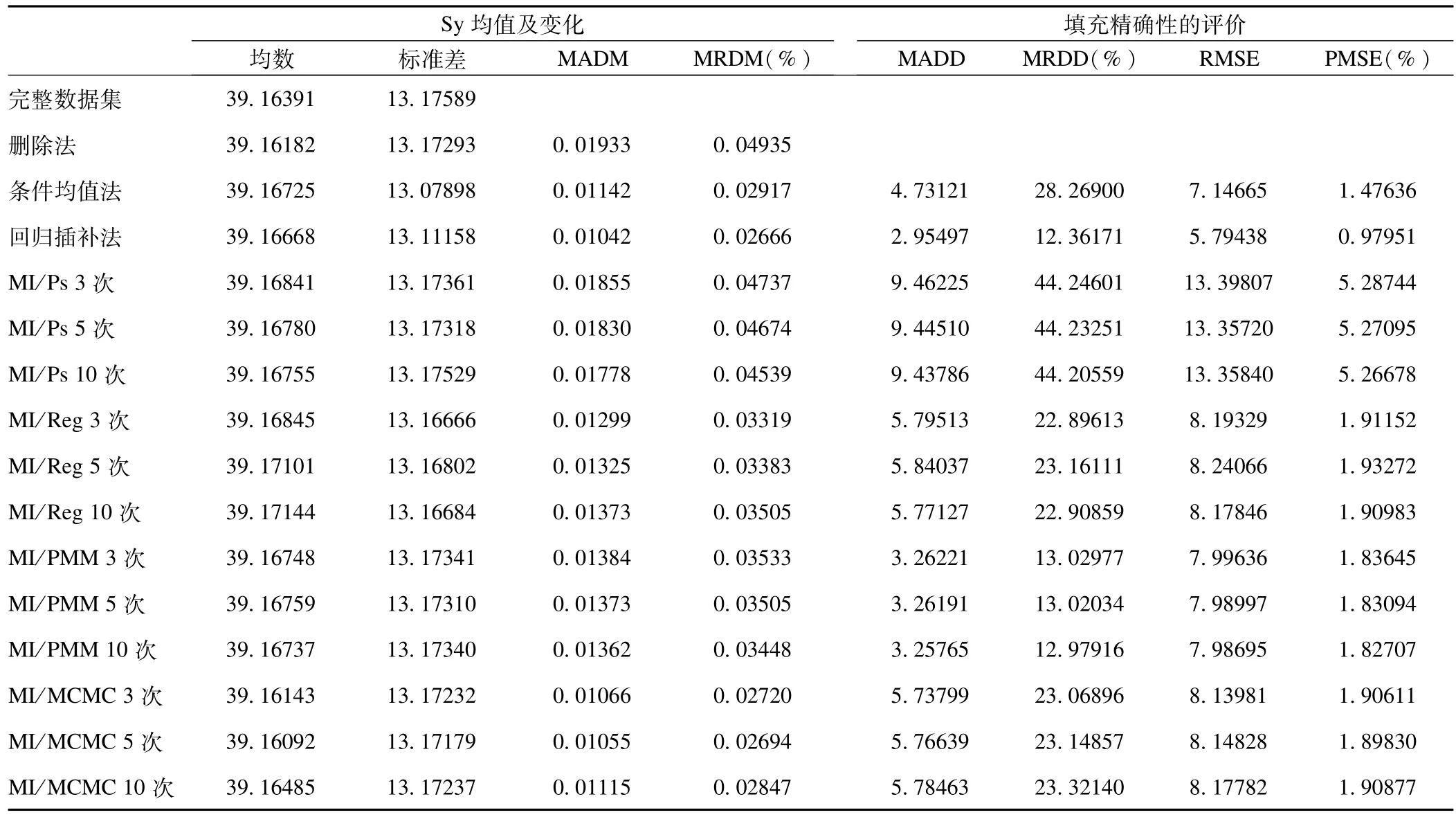
表2 5%缺失率下对sy进行插补后均值的变化及插补精确性

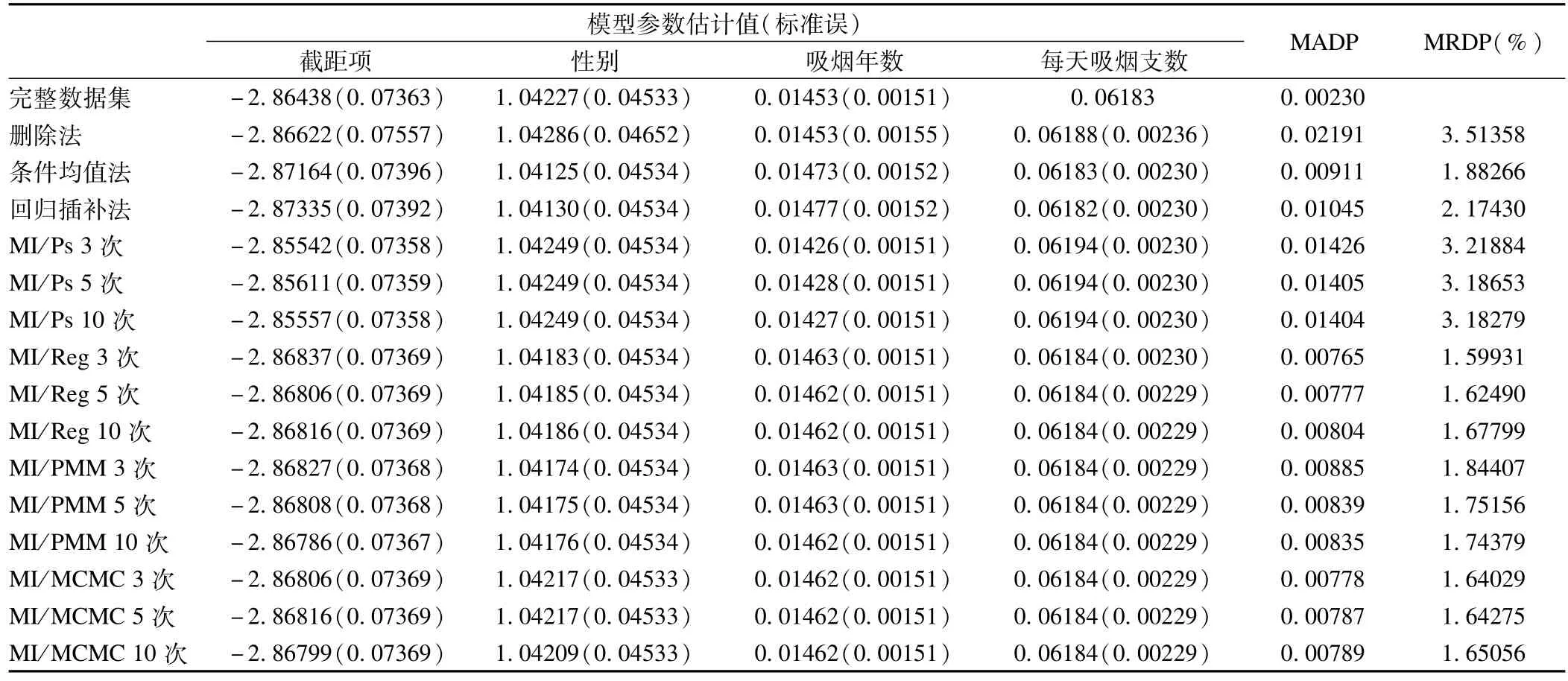
表3 5%缺失率下对sy进行插补后模型参数的变化

由于篇幅限制，其他缺失率下各插补方法的结果不再一一列出，而以简表的形式直观展示不同缺失率下各方法的插补效果。由于同一多重插补方法在不同插补次数下的效果相近，选择插补效果最好时对应的次数列表。

表4显示，sy均值的偏差随着缺失率的增加而增加；在各缺失率下，回归插补sy均值的偏差均最小，删除法的偏差最大；当缺失率≥10%时，各法插补后sy均值偏差的增加速度加快。

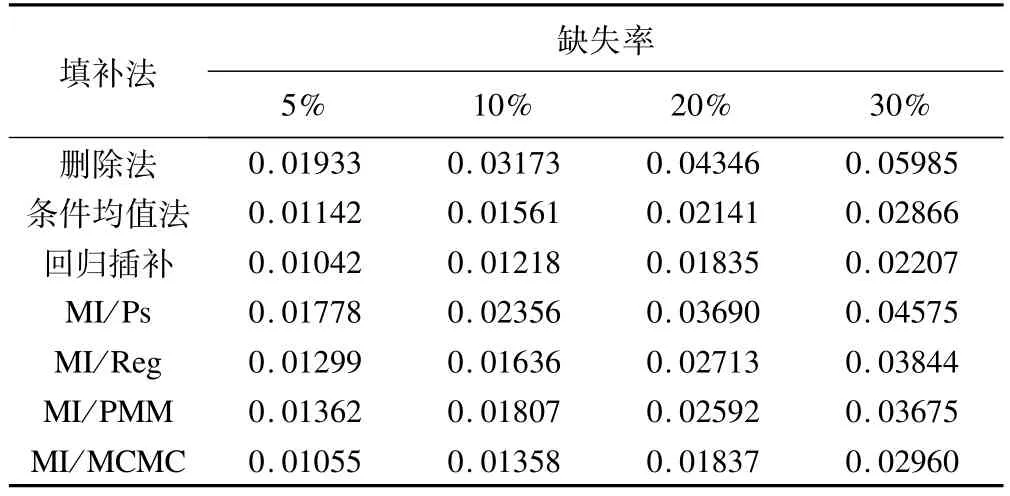
表4 不同缺失率下采用各种方法处理缺失数据后sy均值的平均绝对偏差

表5显示，在各缺失率下，各方法插补值与真实值间的偏差均稳定在某一水平上，回归插补的偏差最小，MI／PS最大。

表6显示，模型参数的偏差随着缺失率的增加而增加。当缺失率为5%时，MI／REG插补后模型参数的偏差最小，缺失率大于5%时，MI／PMM的偏差最小。但各缺失率下MI／REG、MI／MCMC和MI／PMM的插补效果接近，明显优于其他方法，删除法及MI／PS的偏差较大。当缺失率≥10%时，MI／REG、MI／PMM和MI／MCMC模型参数偏差的增长速度加快但不显著，其他方法的增长速度明显加快。

2．多变量缺失

对于多变量缺失，主要结果见表7～11。

表7显示，缺失率为5%时条件均值法sy均值的偏差最小，但与回归插补非常接近，当缺失率大于5%时，回归插补的偏差最小。各缺失率下删除法的偏差最大。

表8显示，各缺失率下，各方法插补值与真实值之间的平均绝对偏差均稳定在某一水平上，且回归插补的偏差最小，MI／MCMC最大。

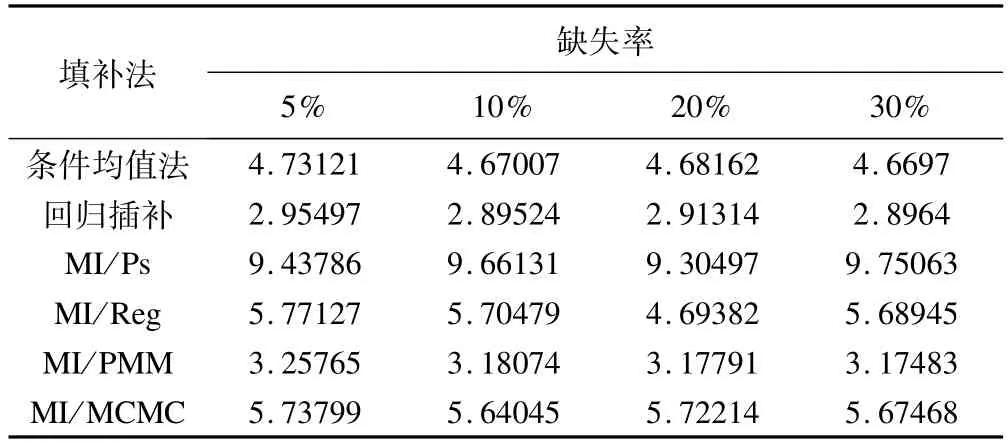
表5 不同缺失率下各种方法插补sy后插补值与真实值的平均绝对偏差

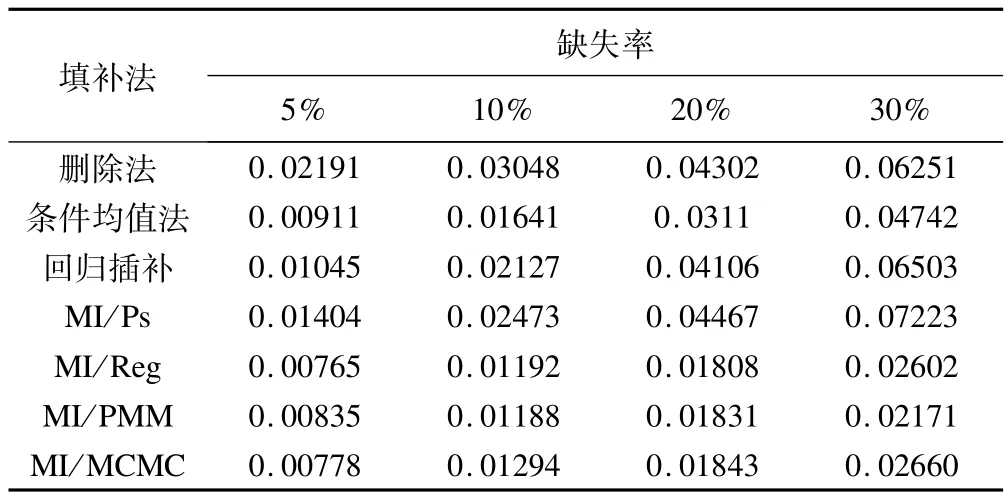
表6 不同缺失率下采用各种方法处理缺失数据模型参数的平均绝对偏差

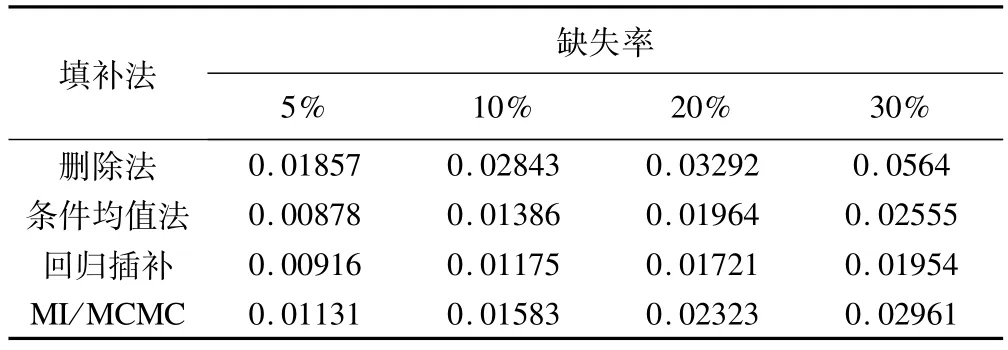
表7 不同缺失率下各法处理缺失数据后sy均值的平均绝对偏差

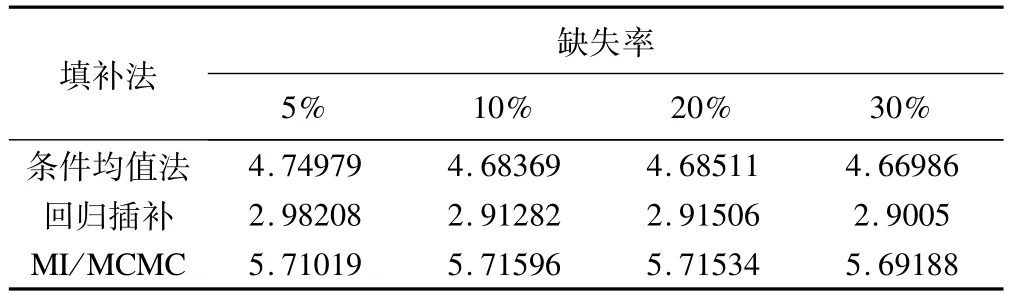
表8 不同缺失率下采用各种方法插补sy后插补值与真实值的平均绝对偏差

表9显示，各缺失率下回归插补与条件均值插补smd均值的平均绝对偏差非常接近且较小，MI／MCMC偏差最大。

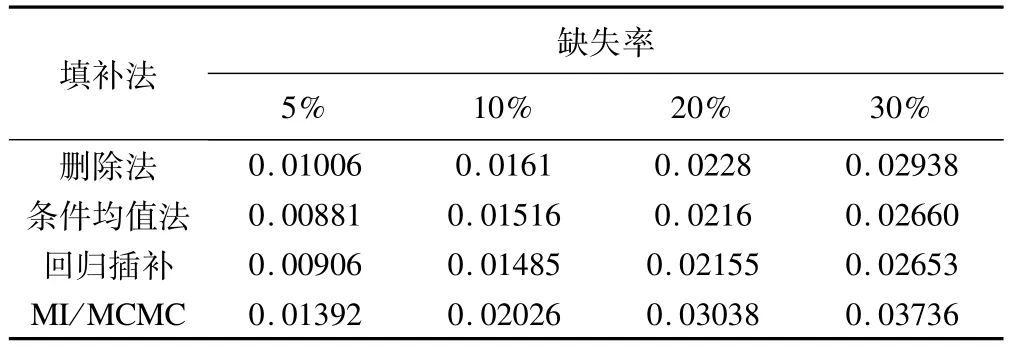
表9 不同缺失率下采用各种方法处理缺失数据后smd均值的平均绝对偏差

表10显示，各缺失率下smd插补值与真实值之间的平均绝对偏差均稳定在某一水平上，条件均值法的偏差最小，MI／MCMC最大。

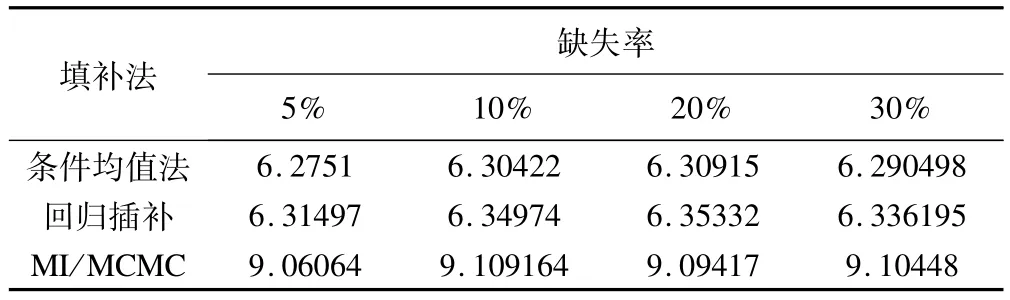
表10 不同缺失率下各种方法插补smd后插补值与真实值的平均绝对偏差

表11显示，各缺失率下条件均值插补后模型参数的平均绝对偏差最小，MI／MCMC最大。当缺失率≥10%时，模型参数偏差增加的速度加快。

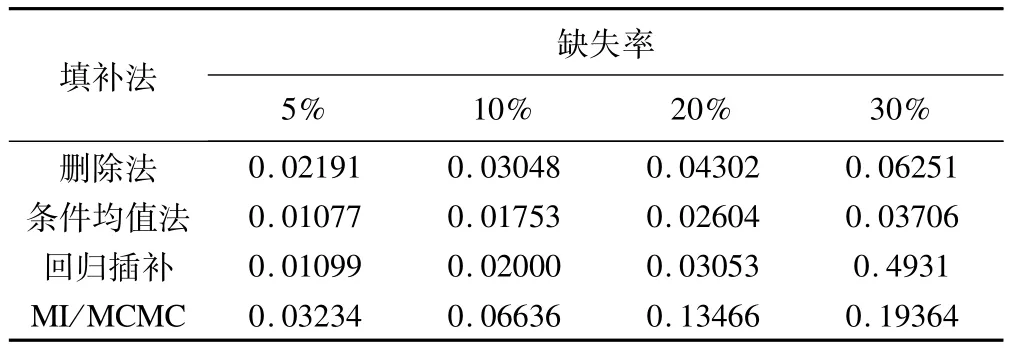
表11 不同缺失率下各种方法插补缺失值后模型参数的平均绝对偏差

讨 论

1．研究结果小结

在实际应用中，完全随机缺失仍不可忽视，会影响研究结果的有效性。缺失率越大，对研究结果影响越大，对各方法插补效果的影响越大，且影响加大的程度也随缺失率的增加而增加，当缺失率≥10%时，缺失变量均值偏差增长的速度、模型参数偏差增长的速度均明显加快。对删除缺失观测后缺失变量均数的相对偏差与模型参数的相对偏差进行比较发现，模型参数的相对偏差远远大于缺失变量均数的相对偏差，提示模型对于数据缺失的敏感性高于缺失变量本身，即缺失数据对模型产生的影响大于对缺失变量均值的影响。尽管依据不同的指标对各缺失值处理方法进行评价、比较会得出不同的结论，但总体来看，插补法处理缺失数据的效果优于删除法，基于统计建模的插补法优于未建模的缺失值处理方法，多重插补法的效果优于单值插补法，缺失率越大优势越显著，这与文献［5，10，12］的研究结果一致，多重插补法处理缺失数据的有效性已得到国内外学者的普遍认可。但本研究是基于较大样本量得到的研究结果，将其推广到小样本情形可能会受到一定限制，因此，在小样本量条件下，数据缺失对研究结果的影响及插补方法的效果值得进一步研究。

2．对各插补方法的思考

本研究中的插补法不仅利用了缺失变量的信息，还利用了辅助变量的信息，辅助变量与缺失变量之间的相关性越强，信息利用越充分，插补的效果越好，如连续变量多变量缺失时采用回归法对sy和smd进行插补时，对sy的插补效果明显要优于对smd的插补效果，这主要是由于辅助变量与sy之间的相关性较好，而与smd的相关性较差。在仅sy缺失条件下，MI／MCMC对sy的插补效果较好，当sy与smd同时缺失时，增加了与其他变量相关性较弱的smd建立马尔可夫链，此时对smd的插补效果较差，同时也影响了对sy的插补效果。MI／REG与MI／PMM均通过拟合回归模型实现多重插补，缺失率较低时（≤10%）两法插补效果接近，但随着缺失率的增加，MI／PMM的插补效果要明显优于MI／REG，这是由于MI／PMM是用数据集中与预测值最邻近的真实值对缺失数据进行插补，使填补更加准确，当缺失率较大和预测值与实际值差异较大时，MI／PMM具有明显的优势。

3．对各插补方法进行比较时评判指标的选择

目前，还没有统一的指标来衡量各缺失数据插补方法的优劣，本研究综合了以往其他研究的指标对插补效果进行评价。结果显示，用不同的指标对各方法插补效果进行评价会得出不同的结论，如对单变量缺失插补时若以吸烟年数sy均值的改变为评价指标，回归法插补效果最好，若以插补后模型参数变化的偏差为评价指标，则MI／PMM、MI／MCMC及MI／REG均较好。因此，在对缺失数据进行插补时，首先明确统计分析的关注点，若进行t检验、方差分析那么应关注缺失变量均值的变化，如果要建立统计模型则更应关注整个模型参数的变化，根据统计分析目的确定评价指标，选择最合适的插补方法。本文讨论了连续型随机变量缺失对研究结果的影响，及相应插补方法的比较，对于离散型随机变量缺失的插补方法及比较将另撰文讨论。

［1］Abraham，Todd W，Russell，et al．M issing data：a review of current methods and applications in epidem iology research．Current opinion in psychiatry，2004，17（4）：315-321．

［2］Streiner DL，Finkle WD．The case of the m issing Data：Methods of dealing with dropouts and other research vagaries．Research Methods in Psychiatry，2002，47（1）：68-75．

［3］吴秋红，张裕青，李国平，等．不同模型处理纵向缺失数据的模拟研究及应用．中国卫生统计，2013，30（6）：855-861．

［4］曹阳，张罗漫．运用SAS对不完整数据集进行多重填补——SAS 9中的多重填补及其统计分析过程（一）．中国卫生统计，2004，21（1）：56-63．

［5］李树威，钟晓妮．基于Markov Chain Monto Carlo模型对医院调查资料中缺失数据的多重估算．中国卫生统计，2013，30（6）：837-841．

［6］SAS Institute Inc．SAS／STAT 9．2 User′s Guide，second edition，North Carolina：SAS Institute Inc，2009．

［7］赵飞，张志杰，刘建翔．疾病监测资料中缺失值最佳填充次数的研究．中国卫生统计，2009，29（5）：455-458．

［8］帅平，李晓松，周晓华，等．缺失数据统计处理方法研究进展．中国卫生统计，2013，30（1）：135-142．

［9］兰妥，江弋，刘光生．基于Sas的时间序列缺失值处理方法比较．计算机技术与发展，2008，10（18）：43-45．

［10］张桥，李宁，张秋菊，等．任意缺失模式缺失数据不同填补方法效果比较，2013，30（5）：690-692．

［11］Preda C，Duhamel A，Picavet M，et al．Tools for Statistical Analysis with M issingData：Application to a Large MedicalDatabase．Connecting Medical Informatics and Bio-Informatics，2005：181-186．

［12］魏昕．缺失数据对微观计量影响研究-以农民收入与消费为例．成都：西南交通大学，2010．

［13］庄严，邢艳春，马文卿．含有缺失机制的多元纵向数据分析．中国卫生统计，2008，25（5）：489-493．

（责任编辑：郭海强）

△通信作者：姜晶梅，E-mail：jingmeijiang238＠hotmail．com