有界变量线性规划问题的一种解法*

刘海英

(福建广播电视大学　福建福州　350003)



有界变量线性规划问题的一种解法*

刘海英

(福建广播电视大学福建福州350003)

摘要：有界变量的线性规划问题可以先转化为标准形式的线性规划问题，然后按照单纯形方法进行求解.但是，由于这类问题增加了变量和等式的约束，从而导致计算量和存储量大大增加.因此，文章考虑先把包含上、下界变量限制的线性规划问题转化为变量有上界限制的线性规划问题，然后再进行求解.

关键词：线性规划，有界变量，单纯形法

在实际应用中的许多线性规划问题，其决策变量具有一定的上、下界限制，这类问题称为有界变量的线性规划问题.有界变量的线性规划问题可以先转化为标准形式的线性规划问题，然后按照单纯形方法进行求解[1-2].但是，由于这类问题增加了变量和等式的约束，从而导致计算量和存储量大大增加.文章利用一种新的解法，可以在不扩大系数矩阵的情况下提高运算效率.

1有界变量线性规划问题基本解的特征

有界变量的线性规划问题的数学模型可写为：

minz=cx

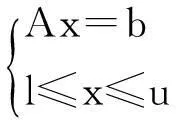
(1)

其中，l=(l1,l2,…,ln)T和u=(u1,u2,…,un)T分别是x=(x1,x2,…,xn)T的下界和上界，矩阵A仍为m×n阶矩阵，并设A的秩为m.

minz=cx

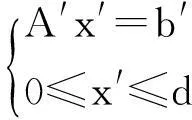
(2)

为表达方便起见，不妨将式(2)仍用x的形式来表示，即

minz=cx

(3)

式(3)称为变量有上界限制的线性规划问题.对于式(3)若引进松弛变量y，则可将其化为标准形式的线性规划问题，即：

minz=cx

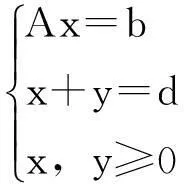
(4)

但这样做之后，系数矩阵会扩大很多，给计算增加困难.下面将介绍一种在不扩大系数矩阵前提下来寻求变上界限制的线性规划问题的解法.

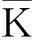
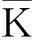
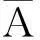
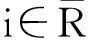
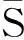
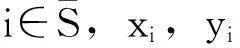
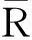
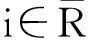
结论5：设S1={i1,i2,…,im}，作矩阵B=(pi1,pi2,…,pim)，则B是满秩的.

由上述结论可知，式(4)的基本解具有这样的特征：在它的前n个分量中，有n-m个分量必取上、下界，而可以不取上、下界的m个分量所对应的矩阵A的列向量必线性无关.由此可以对式(3)的基本解和基本可行解进行如下定义：

(1)B=(pi1,pi2,…,pim)是满秩矩阵；

则称x0为式(3)的一个基本解，B=(pi1,pi2,…,pim)为x0对应的基阵，变量xi1,xi2,…,xim称为相应于该基的基变量，其余变量称为非基变量.另外，称满足约束条件0≤x0≤d的基本解 为基本可行解，称基本可行解对应的基B为式(3)的可行基.

记基变量的指标集为S，非基变量的指标集为R.将指标集合R分成两个子集R1和R2，若满足R1∪R2=R，R1∩R2=Ø，则称(R1,R2)是R的一个剖分，并称{xi|i∈R1}为第一类非基变量，取值都为0；称{xi|i∈R2}为第二类非基变量，取值都为上限di.也就是说，对于R的任一剖分(R1,R2)，非基变量取值为：

(5)

由前面对式(4)基本解的分析及定义容易证明下列定理：

定理2 x0是式(3)的一个基本可行解的充分必要条件是x0是凸集K={x|Ax=b,0≤x≤d}的一个顶点.

定理3 x0是式(2)的一个基本可行解的充分必要条件是(x0,d-x0)是线性规划问题(2)的一个基本可行解.

有了上面的几个定理，下面的两个结论就成为显然的了.

结论6：如果线性规划问题(3)有可行解，则一定有基本可行解.

结论7：如果线性规划问题(3)存在最优解，则一定可以在某个基本可行解上达到最优值.

所以有：XB=B-1b-B-1N1XN1-B-1N2XN2

(6)

将其代入目标函数中，可以得到：

cx=CBXB+CN1XN1+CN2XN2

=CB(B-1b-B-1N1XN1-B-1N2XN2)+CN1XN1+CN2XN2

=CB-1b-(CBB-1N1-CN1)XN1)-(CBB-1N2-CN2)XN2

(7)

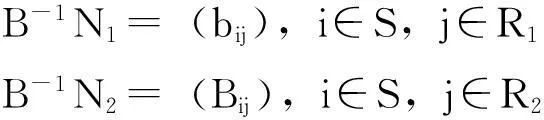
(8)

(9)

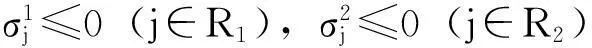
2有界变量单纯形法

和通常的单纯形法一样，这里原算法也是分两个阶段来计算的.第一阶段是寻求一个初始基本可行解，和单纯形法类似[3]，文章不做过多介绍.第二阶段是从初始基本可行解出发，通过基与可行剖分的逐次迭代，不断改进目标函数值，最终获得最优解.

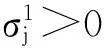
所对应的xk作为换入基变量(如果想提高迭代效率，则从不符合最优性条件的检验数中选取其绝对值最大的对应变量作为换入基变量).由于变量有上界限制，所以换出基变量xl的选择要比单纯形法复杂，具体要考虑问题如下：

(1)如何选取换出基变量.

(2)变量换出以后归入哪一类非基变量.

下面对以上两个问题进行分析.

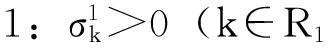
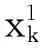
由变量必须为非负值，并且不能超过上界的限制可知，θ应满足：

解该不等式组得：

由此可知：

下面分3种情况进行讨论.

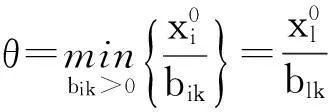
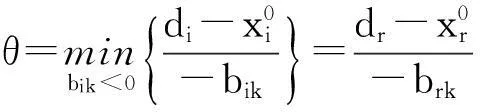
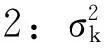
参照情形1进行类似迭代，也应分成如下3种情况：

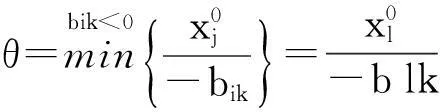
综上可知，不管是哪种情形，都能得出一个新基本可行解x1(如果问题有最优解)，并且x1对应的目标函数值不会超过x0对应的目标函数值.这一结论的验证可查阅参考文献[4].

现在把有界变量单纯形法的计算步骤总结如下：

第1步从一个基本可行解及对应的典式开始.

确定xk的通常规则是在所有不满足最优解条件的检验数中取一个绝对值最大的.如果k∈R1，则转第4步；如果k∈R2，则转第5步.

第4步计算θ=

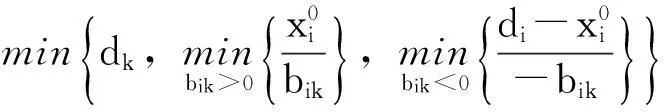
(1)若θ=dk，则转第6步.

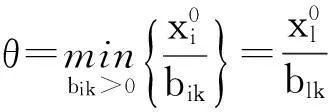
第5步计算θ=

(1)若θ=dk，则转第7步.

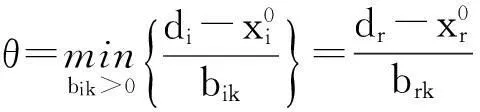
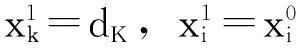
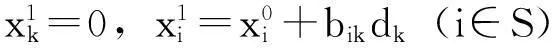
这里假设每个变量都有上界，如果只是部分变量有上界限制，可令没有上界的变量的上界是个充分大的正数，则上述方法同样适用.在计算时不用写出这个充分大的正数，只要在找θ时做个改进就行了.

如果xi的上界是充分大的正数，则：

例1：求解如下线性规划问题[5]：

minz=-2x1-x2

解：第1步 该问题有明显的初始基本可行解x0=(0,0,5,0,21)T，对应的基为B=(p3,p4,p5)，R1={1,2},R2=Ø.列出单纯形表，为方便起见，直接在单纯形表的前边增加一列为解列，用来表示该基本可行解的各基分量值和对应的目标函数值，如表1所示.

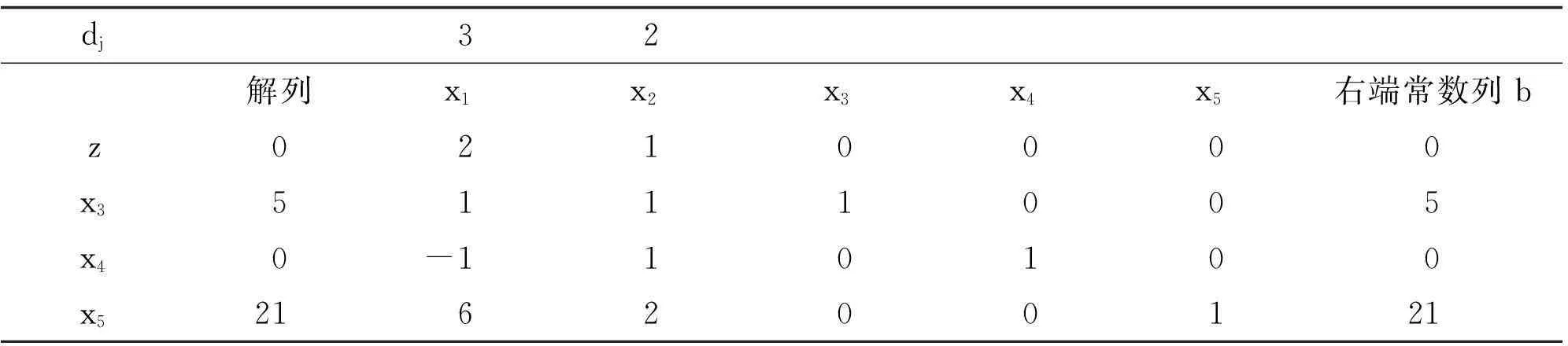
表1　单纯形表1

第3步 取绝对值大的检验数σ1对应的变量x1作为换入基变量.

表2　单纯形表2

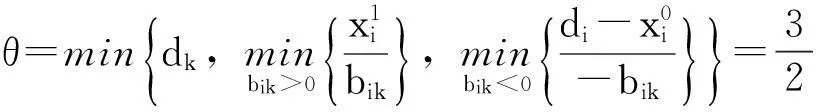
因此，可以确定x5为换出基变量，取值为0，即R1={5},R2{1}，作单纯形表如表3所示.

表3　单纯形表3

因此，取x2为换出基变量.进行一次通常的单纯形迭代(除了解这一列)，对于解列，则有：

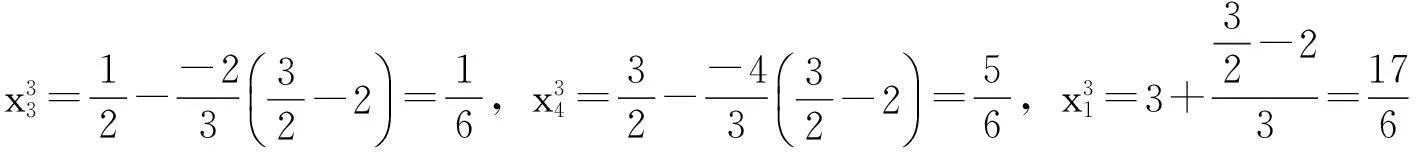
表4　单纯形表4

此时，R1={5},R2={2}.

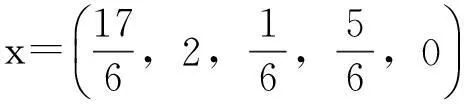
3结论

文章针对线性规划问题中变量有界的情况进行了分析，通过研究基本解的特征，可以把一般形式的有界变量线性规划问题转化为变量有上界限制的问题.然后，进一步提出变量有上界限制的单纯形法，利用文章提出的在不扩大系数矩阵的前提下来寻求变上界限制的线性规划问题的解法，大大减少运算量，提高效率.

参考文献：

[1]唐晓文，刘海英，文斌.线性规划[M].北京：中央广播电视大学出版社，2012.33.

[2]管梅谷，郑汉鼎．线性规划[M]．济南：山东科学技术出版社，1983．56.

[3]中国人民大学数学教研室．线性规划学习指导[M]．北京：中央广播电视大学出版社，1984.153.

[4]钟守南，高成修．运筹学理论基础[M]．武汉：武汉大学出版社，2005．68.

[5]朱求长．运筹学及其应用(第3版)[M].武汉：武汉大学出版社，2004．99.

(责任编辑李佳瑜)

中图分类号：O 29

文献标识码：A

文章编号：1674-9545(2015)04-0077-(07)

通讯作者：刘海英，398118122@qq.com。

收稿日期：2015-9-17

*基金项目：中央广播电视大学非统设课程资助项目成果之一。