带自然边界条件多元多项式样条插值及微分方程数值解

徐应祥

（中山大学新华学院，广东 广州 510520）

一般情况下，大多的偏微分方程很难求得其精确的解析解，因此，如何求其满足要求的近似解，也即数值解，成为科学和工程计算中的最重要内容［1］。求解微分方程的数值方法有很多种，如较流行的差分法、有限元法、边界元法、谱方法与拟谱方法、辛方法等［1－2］。近年来，逐渐兴起另一种求偏微分方程数值解的方法：无网格方法［3－4］。这种数值方法不需要像有限元法一样需要对微分方程的求解区域进行剖分，只是基于在求解区域中选定的某一组散乱分布的点处的信息来确定真解的一种近似，因此其在许多条件下，特别是在高维情形的实现有时要比有限元方法方便。

由于现在对于多元散乱数据拟合方法［5－17］的研究也取得了许多成果，而散乱数据拟合本身就是根据一组给定点确定一个合适的逼近函数，因此将散乱数据拟合的方法应用于偏微分方程数值求解中，可能会带来一些新的可靠的数值方法。文献［1－4，15］讨论了散乱数据拟合方法在求解偏微分方程中的应用，特别是文献［15］在基于径向基的散乱数据拟合方法基础上，对一般的线性偏微分方程给出了基于径向基函数的几种偏微分方程数值求解的泛函信息插值方法的全部过程，并对基于径向基函数的最小二乘方法、配置法、Galerkin方法及Golberg法的基本思想做了总结，这些方法实质都是无网格方法。

本文从任意d元散乱数据出发，给出一种目标泛函较为简单、更符合实际的散乱数据点的多元多项式自然样条。用这种自然样条考虑任意d元散乱数据的插值问题，则该问题的自然样条解与以往不同，其基函数有良好的边界条件与简单的表达式。此外，以这种自然样条为基础，可以构造出一种新的偏微分方程数值方法，数值算例表明这种方法是有效的。

1 散乱数据多元自然样条插值

设表示d个正整数集的直积，对d维多重指标p＝（p1，p2，…，pd）∈，记用Rd表示d维欧氏空间，若u（x）是d元函数，其｜p｜阶导数记为：

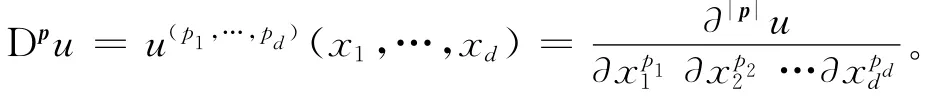
令i＝（i1，i2，…，id）∈，记单项式（x－a）i＝以及i！＝i1！i2！…id！，再记dx＝dx1dx2…dxd及求和符号

给定Rd中含有N个两两不同散乱数据点的集合S＝｛xi｜xi＝（x1i，x2i，…，xdi）∈Rd，i＝1，…，N｝，设方型域以及Sobolev空间X＝Hs（Ω）＝Ws，2（Ω）（s＝｜p｜），显然满足连续嵌入条件s〉d／2。

记Y＝L2（Ω），令Td：X→Y是一个从X到Y的线性算子，定义为：

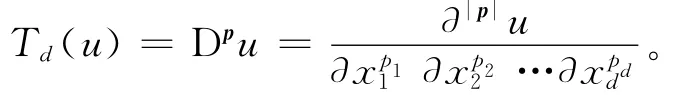
再记BN⊂X是满足如（1）式的自然边界条件的所有u∈X构成的子集。

其中，ipk＝（i1，…，ik－1，pk，0，…，0）；pik＝（p1，…，pk－1，ik，0，…，0）；axk＝（a1，…，ak－1，xk，…，xd）；xaxk＝（x1，…，xk－1，ak，xk＋1，…，xd）；ik＝0，1，…，pk－1。

定义A：X→Z是一个插值算子，满足：Au＝（u（x1），u（x2），…，u（xN））。记Aw＝｛u｜Au＝w，u∈X｝为X中所有满足插值条件Au＝w的函数u的集合，考虑如下插值问题［11］。

问题1 求σ（x）∈X，满足：

问题1称为任意维散乱点带自然边界条件多元样条插值问题，问题的解称为散乱点带自然边界条件多元插值样条，简称多元自然插值样条。

定理1 算子T的核空间为：

反之，用数学归纳法。

（1）当d＝2时，如果u∈N（T2）且满足边界条件（1）式，则T2（u）＝0，即于是有：

（2）假设当d＝m时，如果u∈N（Tm）且满足（1）式，则u（x。 那么当d＝m＋1时，如果u∈N（Tm＋1）且满足边界条件（1）式，则有）＝0，所以），从而由归纳假设可知：

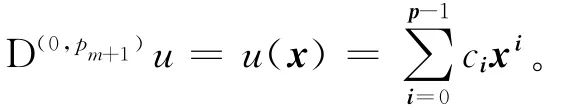
于是对xm＋1积分可得：

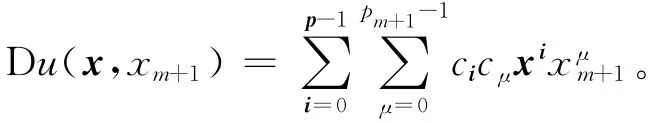
综上可知，对一切d，如果u∈N（Td）且满足边界条件（1）式，则

2 散乱点多元插值自然样条构造

定理2（特征定理）σ∈X是多元插值自然样条的充分必要条件如下：对一切u∈X，Au＝0成立。

证明 记J（u）＝‖Tu‖2，u∈X，Au＝w。一方面，根据泛函取极值的必要条件，若泛函J（σ＋εu）在σ处取极值，则其在σ处的变分δJ＝0，而〉，故 有〈Tdσ，Tdu〉＝0。另一方面，若〈Tdσ，Tdu〉＝0，则J（σ＋εu）＝J（σ）＋ε2‖Td（u）‖2≥J（σ），即J（u）在σ处取极小。

综合上述2个方面，定理得证。

引理1 如果σ∈X是多元插值自然样条，则必存在系数di与ki（i＝1，…，N）使得：

其中，为Td的共轭算子，且有〈ki，u〉＝u（xi）。

证明 记由N（A）＝｛u∈X｜Au＝0｝，即是算子A的核空间，并记N（A）⊥为N（A）在X中的正交补空间，由特征定理可知，当u∈N（A）时有Tdσ，u〉＝ 〈Tdσ，Tdu〉＝0，因 此Tdσ∈N（A）⊥。

对∀u∈X，作泛函λi（u）＝u（xi）（i＝1，…，N），则由Riesz表示定理知存在ki∈X，使得λi（u）＝〈ki，u〉，因此A（u）＝（〈ki，u〉）i＝1，…，N。故若u∈N（A），则有〈ki，u〉＝0，从而有ki∈N（A）⊥，因此｛ki｝i＝1，…，N组成了N（A）⊥的基，而∈N（A）⊥，所 以 存 在 系 数di使 得

定理3（构造定理） 设σ（x）是散乱数据多元自然样条，则其具有如下的显式及紧凑的表达式：

其中，gi（x）为自然样条基函数，即

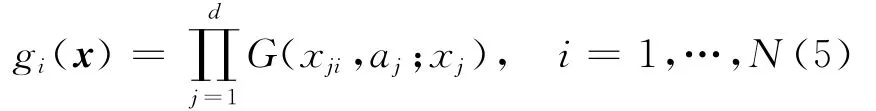
并且有：

其中

（4）式中的系数cj及di满足方程组：

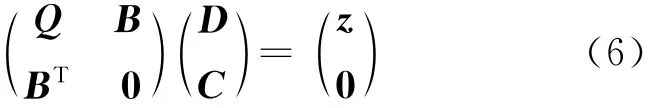
其中，Q＝（gj（xi））对称，而矩阵B＝），C＝（cj）T，D＝（di）T，z＝（w）T，0是零矩阵。

证明 显然xj∈N（Td）（ji≤pi－1－1，i＝1，…，N），所以由引理1可知：

此结果即为BTD＝0。

对任意X中的元素u，在a1点Taylor展开，则有：

类似地，由Taylor展开有：

由自然边界条件（1）式，将上述各式依次代入u中有：

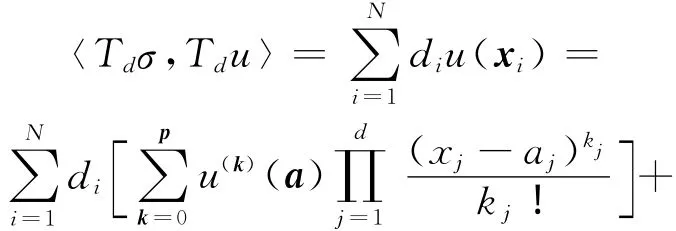
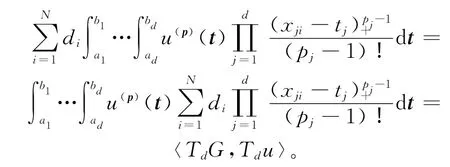
及自然边界条件（1）式，故有：

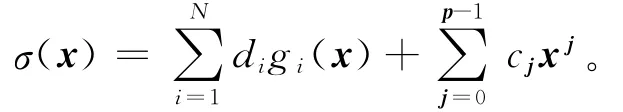
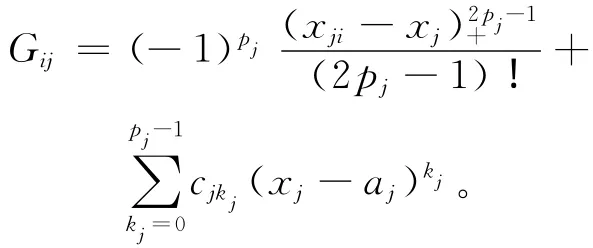
对Gi1，由 自 然 边 界 条 件xd）＝0，可知对任意的x2，…，xd有：

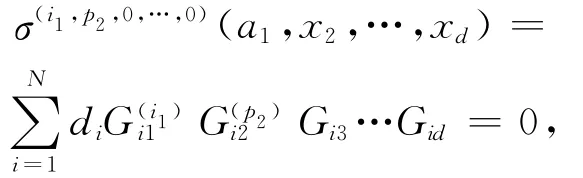
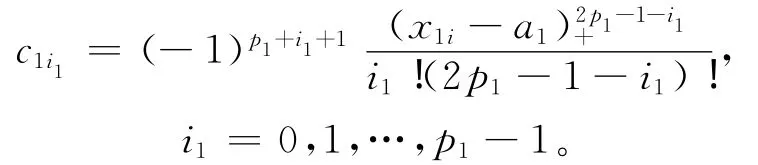
类似地可得c2i2，…，cdkd，形式与c1i1类似，这里不再赘述。再由插值条件Aσ＝w便可得系数cj及di满足方程组（6）式。

在方程组（6）式中，再进行简单验证可知Q是对称的，从而其系数矩阵是对称的。

3 基于自然样条的偏微分方程数值方法

对于给定的偏微分方程，在其求解区域Ω⊂Rd中任意选定一组点，那么由前述可知，以多元多项式自然样条基N）可以作成一个有限维的样条函数空间SN。如果在Galerkin方法中取Vn＝SN，则可以得到一种基于多元多项式自然样条的Galerkin方法。下面以一个具体的含有三元偏微分方程的求解为例来说明这种方法。

其中

令

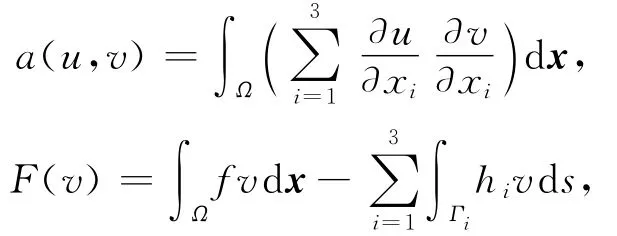
其中，Γi（i＝1，2，3）表示Ω的边界，且xi＝bi，aj≤xj≤bj（j＝1，2，3，j≠i），则方程的广义解u∈H1（Ω）是如（8）式变分问题的解。

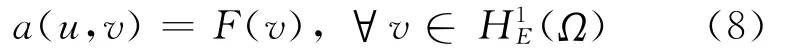
其中，（Ω）为H1（Ω）中满足＝0的所有函数组成的集合。

在Ω中任意选取一组两两不同的点则与这些点相应的多元多项式样条基为gi（x）（i＝1，…，N），由其性质可知满足＝0，因此其张成的函数空间SN⊂（Ω）。于是用SN代替变分问题 （8）式中的（Ω），记uN＝），vn依次取为gi代入方程（8）式，则得关于ci的线性方程组：

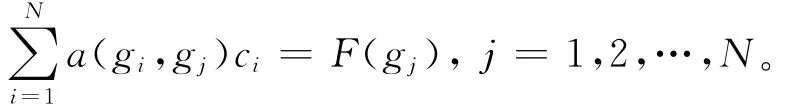
解此线性方程组得ci，再代入uN，即得边值问题（7）式的近似解。

在Ω中随机取220个散乱点，分布如图1所示。选择三元p1＝p2＝p3＝2的自然样条gi（x）张成的子空间SN进行计算，对计算所得的结果，列出当x3＝0.08、0.16、0.24时3种情形下的精确解u、近似解uN及误差r＝u－uN在空间中的截面图形，如图2所示。列出这3种情形下的数值近似解的最大误差与平均误差，见表1所列。

图1 220个散乱点的分布

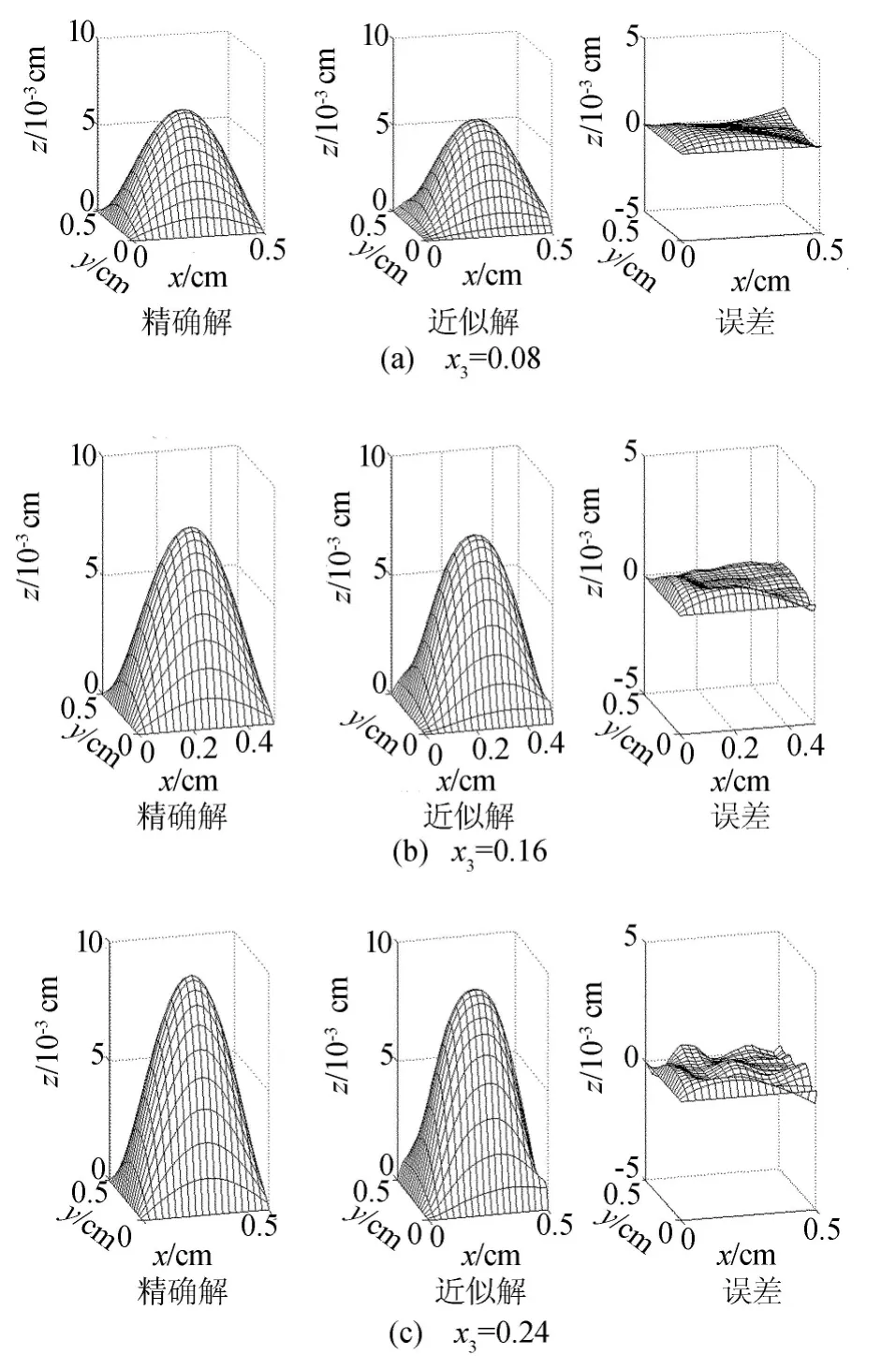
图2 3种情形下精确解u、近似解uN及误差r＝u－uN的曲面

表1 数值解的误差

通过此例结果可以看出，用这样的基于散乱数据的多元样条自然样条函数构造的Galerkin方法是有效的，但针对不同的问题还要注意如下的问题：

（1）在边值问题（7）式中的强加边界条件是齐次边界条件，而基函数gi（x）恰好可能选择使其满足相应的齐次边界条件，因此可以直接进行Galerkin近似。如果边值问题中的边界条件是非齐次的，那么基函数不能直接满足这样的边界条件，从而要使近似解也能满足或近似地满足给定的边界条件就需要对边界条件进行如何处理加以考虑。对于自然边界条件，则根据多元函数的Green公式等适当构造泛函，使其在变分过程能自动满足［16－18］。而强加的非齐次边界条件可以用补偿法将其改造成一个近似的自然边界条件，或用Lagrange乘子法将其吸收进变分过程，从而达到去掉强加边界的目的［16－18］。

（2）对于基函数gi（x），由其构造可知，其在方型区域某些边界上能够自动满足一些齐次边界条件。因此，在具体问题中，对于相应的方型区域上的齐次边界条件可以选择或重新构造基函数使其能满足齐次边界条件，从而尽可能减少因要对边界的处理而要在变分方程中增加一些项。

（3）散乱点的选取可以在区域内部，也可在边界上，但要尽可能使散乱点均匀分布，从而使近似解更能反应方程所反映问题的信息和特征。

［1］ Reutskiy S Y.A boundary method of Trefftz type for PDEs with scattered data［J］.Engineering Analysis with Boundary Elements，2005，29：713－724.

［2］ Bouhamidi A，Jbilou K.Meshless thin plate spline methods for the modified Helmholtz equation［J］.Comput Methods Appl Mech Engrg，2008，197：3733－3741.

［3］ Duan Y.A note on the meshless method using radial basis functions［J］.Computers and Mathematics with Applications，2008，55：66－75.

［4］ Firoozjaee A R，Afshar M H.Discrete least squares meshless method with sampling points for the solution of elliptic partial differential equations［J］.Engineering Analysis with Boundary Elements，2009，33：83－92.

［5］ Kazhdan M，Bolitho M，Hoppe H.Possion surface reconstruction［C］／／Proceeding of Eurogaphics Symposium on Geometry Processing，Cagliari，Italy，2006：61－70.

［6］ Guan L T，Liu Bin.Surface design by natural splines over refined grid points［J］.Journal of Computational and Applied Mathematics，2004，163（1）：107－115.［7］ Lai M J，Schumaker L L.Spline functions over triangulations［M］.London：Cambridge University Press，2007：1－10.

［8］ Lai M J.Multivarariate splines for data fitting and approximation［M］／／Neamtu M，Schumaker L L.Approximation Theory XII，San Antonio 2007.Brentwood：Nashboro Press，2008：210－228.

［9］ Zhou T H，Han D F，Lai M J.Energy minimization method for scattered data Hermit interpolation［J］.Applied Numerical Mathematics，2008，58：646－659.

［10］ Chui C K，Guan L T.Multivariate polynomial natural spline for interpolation of scattered data and other applications［C］／／Conte A，et al.Workship on Computational Geometry.World Scientific，1993：77－98.

［11］ Guan L T.A local basis for bivariate polynomial natural splines of scattered data［C］／／Guangzhou International Symposium of Computational Mathematics，1997：10－20.

［12］ Guan L T.Bivariate polynomial natural spline interpolation algorithms with local basis for scattered Data［J］.Jounal of Computational Analysis and Applications，2003，45I（1）：77－101.

［13］ Laurent P J.Approximation et optimization［M］.Paris：Hermann，1972：50－56.

［14］ Bezhaev A Y，Vasilenko V A.Variational theory of splines［M］.New York：Kluwer Academic／Plenum Publishers，2001：45－60.

［15］ Wu Z.Model，method and theory of scattered data fitting［M］.Beijing：Science Press，2007：75－90.

［16］ 陈艳秋，王家正.三角网格上的Lagrange－Stieltjes型有理插值［J］.合肥工业大学学报：自然科学版，2013，36（9）：1144－1147.

［17］ 李少华，唐 烁，丁 晨.S－型非均匀有理 TC－双弧的G2Hermit插值［J］.合肥工业大学学报：自然科学版，2014，37（12）：1523－1527.