随机激励下非线性空气悬架系统的混沌振动分析

王靖岳， 王浩天， 郭立新

（1.沈阳理工大学 汽车与交通学院，辽宁 沈阳 110159；2.沈阳航空航天大学 自动化学院，辽宁 沈阳 110136；3.东北大学 机械工程与自动化学院，辽宁 沈阳 110819）

由于汽车悬架系统广泛采用空气弹簧、电流变阻尼、干摩擦阻尼和磁流变阻尼等元器件，所以系统具有明显的非线性，可能导致悬架系统发生混沌振动，这已成为国内外学者研究的热点问题［1－5］。文献［6］对非线性汽车悬架系统进行了近似线性处理，指出了发生Hopf分岔时线性系统失稳，研究了周期扰动下系统的拟周期、分谐波和混沌运动；文献［7］采用非线性曲线拟合方法代替气体状态方程，得到了工作条件下空气弹簧刚度的工作曲线方程；文献［8］考虑了汽车运行中重力项的影响，采用Melnikov函数研究了1／4汽车系统的全局同宿轨道分岔以及通往混沌的道路；文献［9］在研究客车空气悬架过程中提出了采用拟合的办法确定空气弹簧的变刚度；文献［10］采用干摩擦理想模型模拟非线性弹簧力和阻尼力，并研究了汽车系统中出现的混沌运动；文献［11］利用气体状态方程研究了空气悬架的振动模型和刚度特性；文献［12］利用空气弹簧有限元模型拟合出其受力曲线，分析了单频正弦激励下汽车空气弹簧悬架的四自由度半车模型的非线性行为。

本文在以上研究的基础上，考虑阻尼减振器的阻尼非线性和空气弹簧的非线性，建立1／4汽车空气悬架系统的单自由度非线性动力系统模型。以某客车为例，揭示路面不平度激励幅值、激励频率、减振器阻尼系数和非线性阻尼系数对系统中分岔和混沌运动的影响。

1 系统的模型和运动微分方程

当仅考虑汽车悬架系统的平顺性时，可将汽车简化成单自由度1／4汽车悬架模型，如图1所示。该系统由簧载质量、空气弹簧和阻尼减振器组成。其中，m为车身质量。

图1 单自由度1／4汽车模型

在空气悬架系统的下方施加一个随机路面激励作为输入［13］，即

其中，a为路面不平度激励幅值；σ为激励频率白噪声强度；ξ（t）为标准正态白噪声；ω为激励频率；x（t）为车身质量上的位移输出。则有：

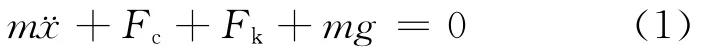
其中，Fc为阻尼力，且，c为阻尼系数，c1为非线性阻尼系数；Fk为空气弹簧对车身质量m的作用力，且有［14－16］：

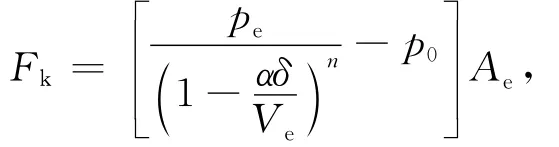
其中，n为气体多变指数；α为空气弹簧体积变化率；p0为大气压力；pe为空气弹簧压力；δ为空气弹簧的变形位移；Ve为空气弹簧的体积；Ae为空气弹簧有效面积。δ＝x0－x，可得˙δ＝˙x0－˙x，¨δ＝¨x0－¨x，代入（1）式，并令n＝1，整理后得到非线性空气悬架系统振动的微分方程为：

其中，弹性力为：

当δ＝0时，f（0）＝peAe－p0Ae－mg，由于在平衡状态时满足peAe－p0Ae＝mg，即f（0）＝0。而，则f′（0）＞0。

利用泰勒公式将（2）式简化，弹性力项f（δ）在δ＝0处进行泰勒展开，舍去高阶无穷小项o（δ3），整理后得：

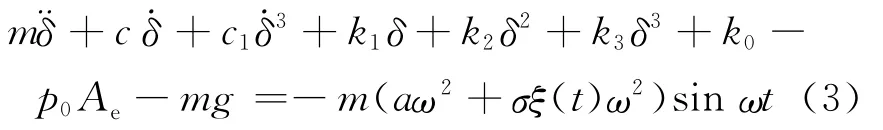
其中

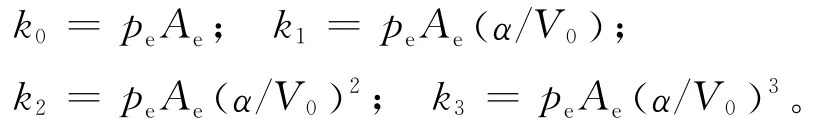
平衡状态时有peAe－p0Ae＝mg，所以k0－p0Ae－mg＝0，则（3）式可进一步简化为：

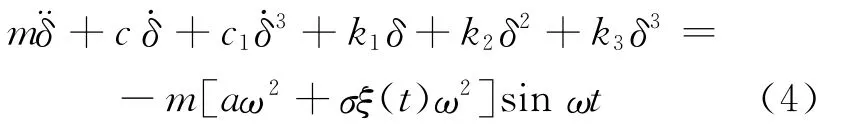
令z1＝δ，z2＝˙δ，则（4）式的状态方程为：

2 分岔与混沌分析

2.1 激励幅值对系统分岔和混沌的影响

选 取 某 客 车 系 统 参 数 如 下［14，17］：m＝5 456kg，pe＝5×105Pa，Ae＝0.033 5m2，α＝1.8，Ve＝0.008 62m3，c＝7 400N／（m·s－1），c1＝650N／（m·s－3），ω＝12.56rad／s。初始条件为：z1（0）＝0，z2（0）＝0。用 4－5 阶 Runge－Kutta法对（2）式进行数值积分，得到系统在路面不平度激励幅值a∈（0，0.10）时的分岔图，如图2所示。当a∈（0，0.036）时，系统作周期1运动；取a＝0.02m时，如图3所示，相图为封闭曲线，Poincaré映射图为1个点，时间历程曲线规则有序，功率谱图为离散谱，经计算Lyapunov指数λ1＝ － 0.675 272、λ2＝ － 0.683 154。 当a＝0.028 5m时，系统发生跳跃现象，振幅和速度发生巨大的变化，汽车的平顺性和舒适性变差。随着路面不平度激励幅值a的增大，当a＝0.036 4m时，系统发生倍周期分岔，开始作周期2运动；取a＝0.04m时，如图4所示，相图为封闭曲线，Poincaré映射图为2个点，时间历程曲线规则有序，功率谱图为离散谱，经计算Lyapunov指数λ1＝－0.674 621、λ2＝－0.685 011。当a＝0.043 7m时，系统又作周期1运动；取a＝0.06m时，可得系统的相图、Poincaré映射图、时间历程曲线和功率谱图，如图5所示，Lyapunov指数λ1＝－0.677 860、λ2＝－0.684 910。当a＝0.069 3m时，系统再次发生跳跃现象。当a＝0.078 9m时，系统发生倍周期分岔，从周期1运动转迁为周期2运动；取a＝0.083m时，如图6所示，相图为封闭曲线，Poincaré映射图为2个点，时间历程曲线规则有序，功率谱图为离散谱，Lyapunov指数λ1＝－0.566 086、λ2＝－0.576 651。当a＝0.084 4m时，系统经倍化分岔由周期2运动转迁为周期4运动。随着路面不平度激励幅值a的增大，当a＝0.085 6m时，系统经倍化分岔由周期4运动变为混沌运动；取a＝0.086m时，如图7所示，相图曲线是不封闭的，Poincaré映射为自相似的点集，时间历程曲线无规律，功率谱图为离散谱，Lyapunov指数λ1＝0.565 287、λ2＝－0.577 094。当a＝0.086 8m时，系统由混沌运动退化为周期3运动；取a＝0.09m时，如图8所示，相图为封闭曲线，Poincaré映射图为3个点，时间历程曲线规则有序，功率谱图为离散谱，Lyapunov指数λ1＝－0.666 329、λ2＝－0.695 184。当a＝0.091 2m时，系统由周期3运动变为混沌运动。取a＝0.098m时，如图9所示，相图曲线是不封闭的，Poincaré映射为自相似的点集，时间历程曲线无规律，功率谱图为离散谱，λ1＝0.599 936、λ2＝－1.962 349。

以上分析表明，汽车在平坦的路面行驶不会发生混沌运动，当遇到凸凹不平的路面时会发生混沌运动，这与文献［12］分析结果一致。

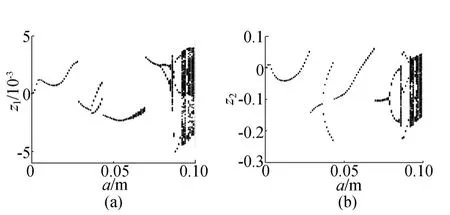
图2 路面不平度激励幅值a∈（0，0.10）时系统分岔图

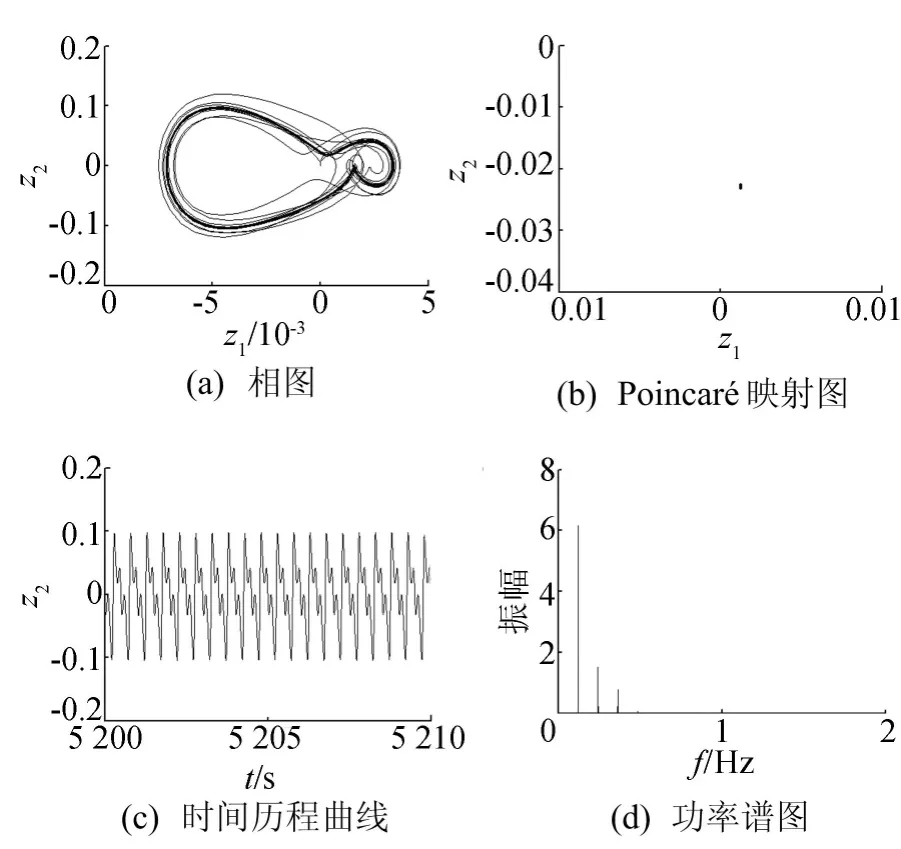
图3 a＝0.02m时系统各参数曲线和图谱

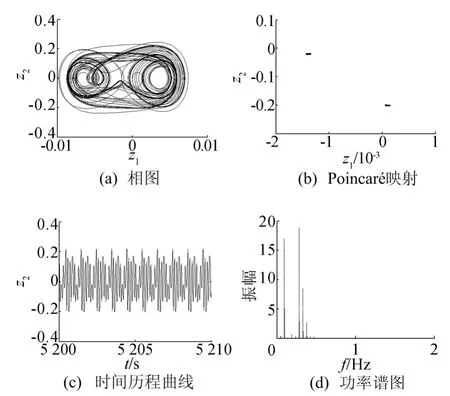
图4 a＝0.04m时系统各参数曲线和图谱

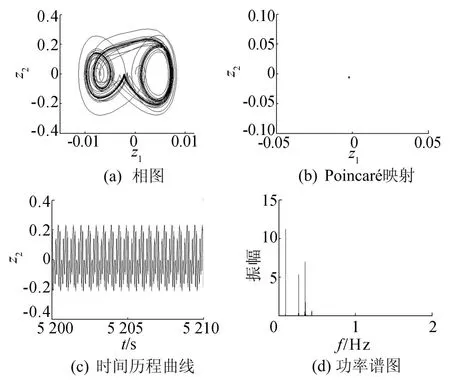
图5 a＝0.06m时系统各参数曲线和图谱

图6 a＝0.083m时系统各参数曲线和图谱

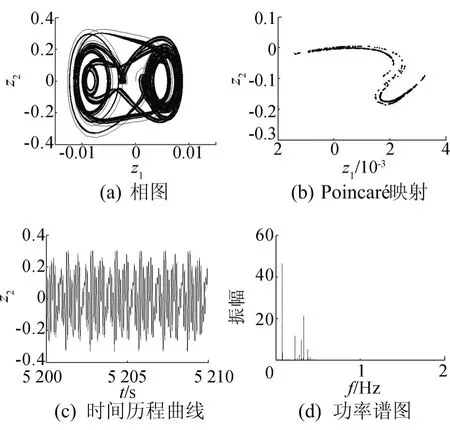
图7 a＝0.086m时系统各参数曲线和图谱

2.2 激励频率对系统分岔和混沌的影响

图8 a＝0.09m时系统各参数曲线和图谱

图9 a＝0.098m时系统各参数曲线和图谱

其他参数不变，路面不平度激励幅值a取0.02m，以激励频率f为分岔参数，可得系统在f∈（0，5）时的分岔图，如图10所示。取f＝4.0Hz时，如图11所示，相图为封闭曲线、Poincaré映射图为1个点、时间历程曲线规则有序，功率谱图为离散谱，经计算Lyapunov指数λ1＝－0.679 888、λ2＝－0.687 029；可见，系统作周期1运动；从图10可以看出，随着激励频率f的减小，当f＝3.24Hz时系统经过分岔作周期2运动；当f＝3.0Hz时，相图为封闭曲线，Poincaré映射图为2个点，时间历程曲线规则有序，功率谱图为离散谱，Lyapunov指数λ1＝－0.674 696、λ2＝－0.684 574。当f＝2.48时，系统又从周期2运动到周期1运动。取f＝1.0Hz时，系统相图、Poincaré映射图、时间历程曲线和功率谱图，如图12所示；经计算Lyapunov指数λ1＝ －0.673 944、λ2＝ －0.684 167。在（1.50，2.48）上，系统发生了跳跃现象，振幅突然变化。由于存在跳跃和分岔现象，因而参数的变化将引起系统不同的运动状态，有必要对其他参数进行分析［12］。

图10 以激励频率f为分岔参数的分岔图

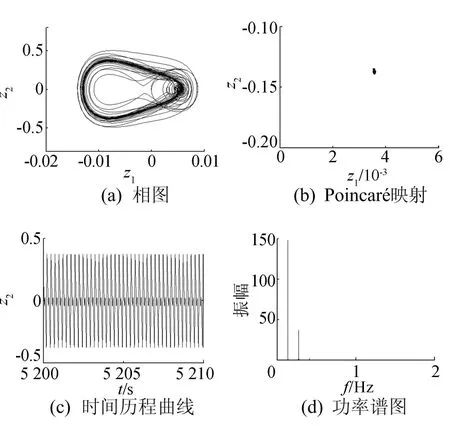
图11 当f＝4.0Hz时系统各参数曲线和图谱

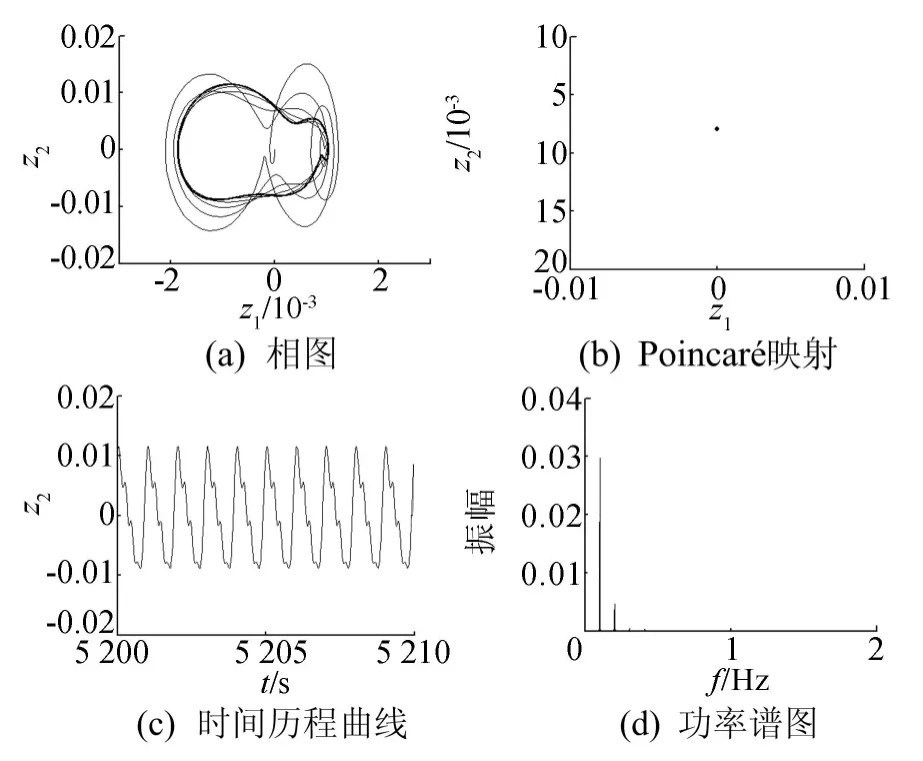
图12 f＝1.0Hz时系统各参数曲线和图谱

2.3 阻尼系数对系统分岔和混沌的影响

其他参数不变，取a＝0.04m，以阻尼系数c为分岔参数得到系统分岔图，如图13所示。当c∈（0，300）时，系统作混沌运动；取c＝100N／（m·s－1）时，如图14所示，系统的相图为不封闭曲线，Poincaré映射图为自相似的点集，时间历程曲线无规律，功率谱图为连续谱，经计算Lyapunov指数λ1＝0.604 113、λ2＝－0.627 275。

当c∈（300，10 000）时，系统作周期2运动；取c＝6 000N／（m·s－1）时，如图15所示，系统的相图为封闭曲线，Poincaré映射图为2个点，时间历程曲线规则有序，功率谱图为离散谱，经计算Lyapunov 指 数λ1＝ － 0.551 344、λ2＝－0.552 031。可见在小阻尼范围内，汽车容易出现混沌运动，这与文献［12］分析结果一致。

图13 阻尼系数c为分岔参数的分岔图

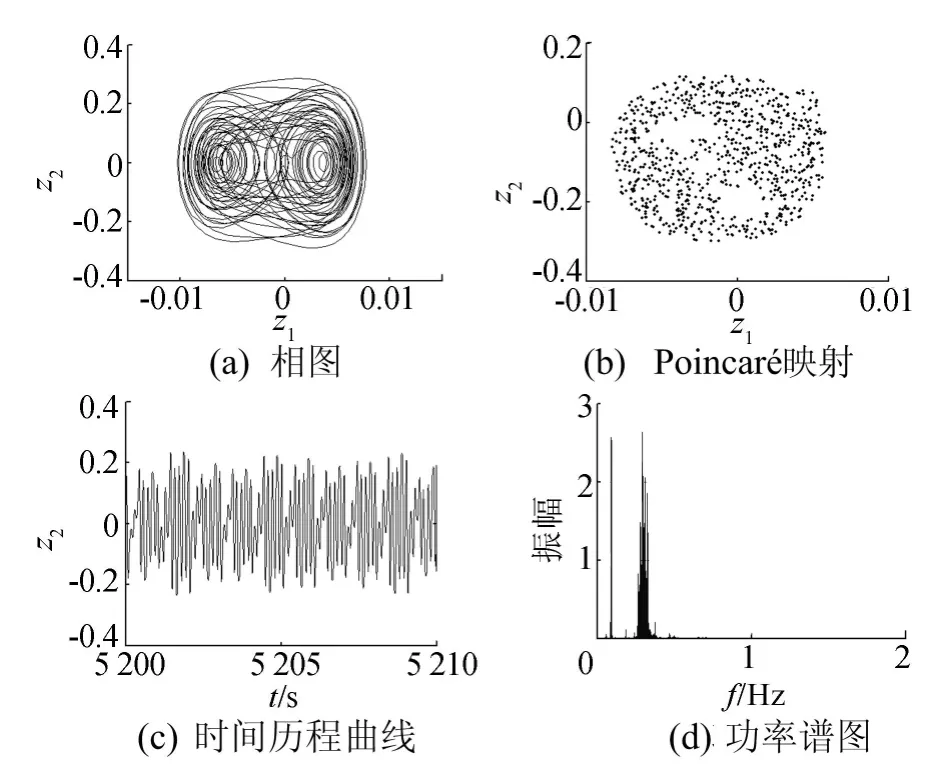
图14 c＝100N／（m·s－1）时系统各参数曲线和图谱

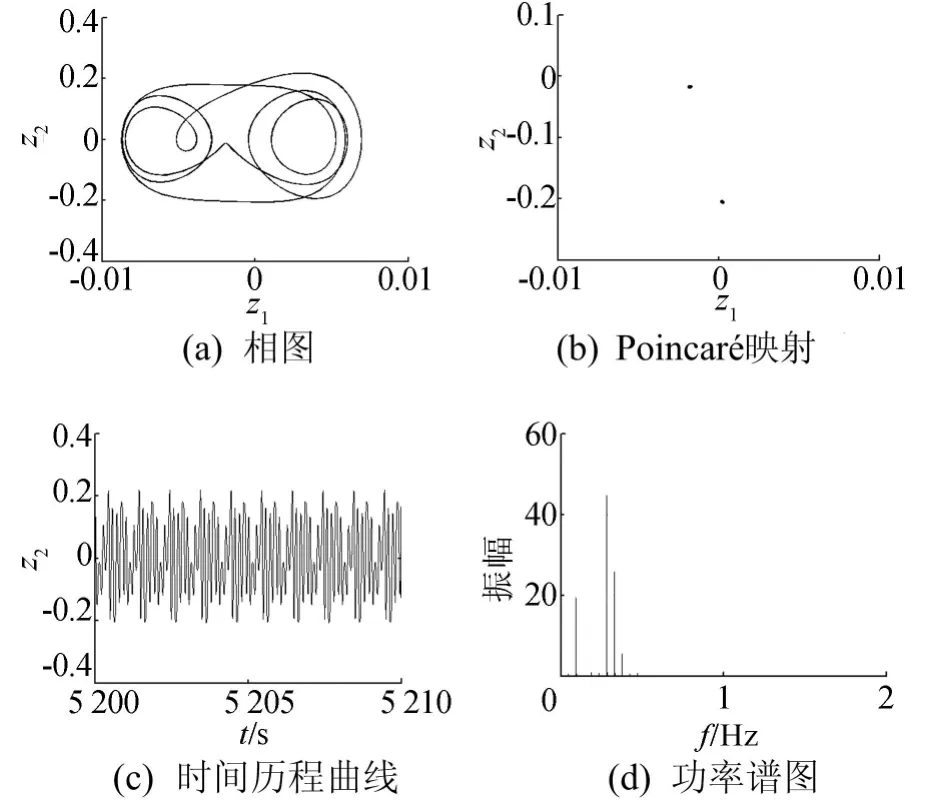
图15 c＝6 000N／（m·s－1）时系统各参数曲线和图谱

2.4 非线性阻尼系数对系统分岔和混沌的影响

其他参数不变，取a＝0.04m，f＝2.0Hz，以阻尼系数c1为分岔参数得到系统的分岔图，如图16所示。取c1＝500N／（m·s－3）时，如图17所示，系统的相图为封闭曲线，Poincaré映射图为2个点，时间历程曲线规则有序，功率谱图为离散谱，经计算Lyapunov指数λ1＝－0.673 366、λ2＝－0.685 181，系统作周期2运动。可见在此汽车参数下，非线性阻尼对汽车的分岔和混沌运动影响较小。

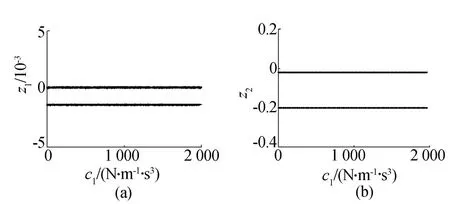
图16 以阻尼系数c1为分岔参数分岔图

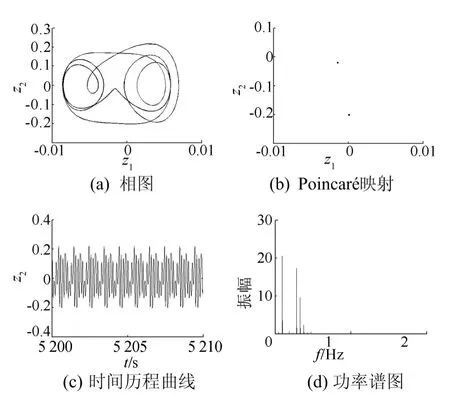
图17 c1＝500N／（m·s－3）时系统各参数曲线和图谱

3 结束语

基于阻尼减振器的阻尼非线性和空气弹簧的非线性建立起来的1／4汽车空气悬架系统在随机路面激励作用下确实存在混沌和分岔现象。路面不平度激励幅值越大，汽车发生混沌的可能性越大；激励频率在某个特定区间容易发生跳跃现象和分岔；减振器阻尼系数越小，系统越容易发生混沌；非线性阻尼系数对系统影响较小。通过合理选择汽车结构参数，避开汽车发生分岔和混沌的区域，可以提高汽车的平顺性和舒适性。本文可为汽车悬架参数的匹配设计提供参考。

［1］ Murata A，Kume Y，Hashimoto F.Application of catastrophe theory to forced vibration of a diaphragm air spring［J］.Journal of Sound and Vibration，1987，112（1）：31－44.

［2］ Stammers C W，Sireteanu T.Vibration control of machines by use of semi－active dry friction damping［J］.Journal of Sound and Vibration，1998，209（4）：671－684.

［3］ Sut M S，Yeo M S.Development of semi－active suspension systems using ER fluids for the wheeled vehicle［J］.Journal of Intelligent Material Systems and Structures，1999，10（9）：743－747.

［4］ Ni Y Q，Cheny，Ko J M，et al.Neuro－control of cable vibration using semi－active magneto－rheological dampers［J］.Engineering Structures，2002，24（3）：295－307.

［5］ 盛 云，吴光强.汽车非线性悬架的混沌研究［J］.汽车工程，2008，30（1）：57－60.

［6］ Liu Z，Payre G，Bourassa P.Stability and oscillations in a time－delayed vehicle system with driver control［J］.Nonlinear Dynamics，2004，35（2）：159－173.

［7］ Chen L，Zhou K H，Li Z X.Dynamic characteristics fitting of air springs and numerical analysis of air suspensions with variant stiffness［J］.Journal of Mechanical Engineering，2010，46（4）：93－98.

［8］ Litak G，Borowiec M，Friswell M I，et al.Chaotic vibration of a quarter－car model excited by the road surface profile［J］.Communications in Nonlinear Science and Numerical Simulation，2008，13（7）：1373－1383.

［9］ 胡 芳.非线性空气悬架模型的理论研究及实车试验［J］.合肥 工 业 大 学 学 报：自 然 科 学 版，2007，30（11）：1429－1432.

［10］ Zhu Q，Ishitobi M.Chaos and bifurcations in a nonlinear vehicle model［J］.Journal of Sound and Vibration，2004，275（3）：1136－1146.

［11］ 尹万建，杨绍普，申永军，等.空气弹簧悬架的振动模型和刚度特性研究［J］.北京交通大学学报：自然科学版，2006，30（1）：71－74.

［12］ 黄巨成，屠德新，魏道高.汽车空气悬架非线性垂向动力学行为研究［J］.合肥工业大学学报：自然科学版，2013，36（6）：641－645.

［13］ 杨绍普，李韶华，郭文武.随机激励滞后非线性汽车悬架系统的混沌运动［J］.振动、测试与诊断，2005，25（1）：22－25，71.

［14］ 方瑞华.汽车空气悬架非线性振动理论和试验［J］.农业机械学报，2007，38（7）：13－15，38.

［15］ Malin P.Derivation of air spring model parameters for train simulation［D］.Lulea：Lulea University of Technology，2002.

［16］ Toyofuku K，Yamada C，Kagawa T，et al.Study on dynamic characteristic analysis of air spring with auxiliary chamber［J］.JSAE Review，1999，20（3）：349－355.

［17］ 郭二生.空气悬架大客车操纵稳定性和行驶平顺性仿真与试验研究［D］.长春：吉林大学，2005.