反三角分块矩阵的群逆存在性和表达式

夏玲玲， 邓 斌

（合肥工业大学 数学学院，安徽 合肥 230009）

设Cn×n是n×n阶复矩阵的集合。矩阵A的Drazin逆［1］是存在并且唯一的，表示为AD，满足以下3个方程：

其中，k是满足rank（Ak）＝rank（Ak＋1）的最小非负整数，称为A的指数，记为ind（A）。若ind（A）＝1，称A是群逆的，记为A＃。另外记Aπ＝I－AA＃，A0＝I。

对于分块矩阵群逆的研究一直是矩阵研究中一个重要的课题。文献［2］给出了2×2分块矩阵Drazin逆的表达式，其中A、D是方阵。但是，这一问题到目前为止还没有得到具体解决。当D＝0时，

对于M的Drazin逆（群逆）的研究也激起了很多人的兴趣，却没有一个明确的结果。文献［3］给出了体上某些分块矩阵的群逆的存在性定理及其表达式；在文献［4－8］中分别给出了反三角分块矩阵在一些条件下的群逆的存在性和表达式及块k－循环矩阵带W权的Drazin逆表达式；在文献［9］中得到了2个幂等矩阵的一般组合可逆的充要条件，在文献［10］中对之前的结论进行了推广，研究了2个幂等矩阵的组合群逆问题。

本文给出了在条件P2Q＝0，PQ＋QP＝0和P2Q＝0，QPπ＝0下（P＋Q）＃的表达式，并应用得到的结论给出了的表达式。然后，主要探究复数域上反三角分块矩阵在不同情况下群逆存在性和表达式。

1 主要引理

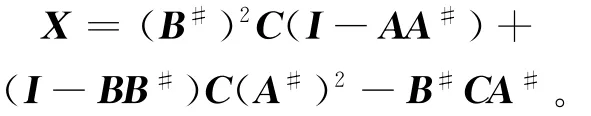
引理2 令A，B∈Cn×n满足AB＝BA＝0，若（A＋B）＃、A＃、B＃存在，则（A＋B）＃＝A＃＋B＃。

引理3 令A，B∈Cn×n，A＃、B＃存在，则有：

（1）若R是非奇异矩阵，B＝RAR－1，则B＃＝RA＃R－1。

（2）存在一个非奇异矩阵R，使得A1∈Cr×r是非奇异矩阵，A2∈C（n－r）×（n－r）是幂零矩阵，且

引理4 令M∈Cn×n，满足B∈Cp×（n－p），C∈C（n－p）×p，则M＃存在的充要条件是r（B）＝r（C）＝r（BC）＝r（CB），且M＃＝

引理5 令A、B、C、D是m×n，m×k，l×n，l×k矩阵，则有［11］：

（1）r（A，B） ＝r（A）＋r（EAB）＝r（EBA）＋r（B）。

其中，SA＝D－CA†B，EA＝I－AA†，FA＝IA†A。

引理6 令N＝，B＝EB，C＝1A1CFA，JD＝EC1SAFB1，SA＝D－CA（1）B，则有［12］：

（1）r（N）＝成立的充要条件是成立。

（2）r（N）＝r（A，B） ＋r（C，D）成立的充要条件是成立。

2 定理与证明

定理1 已知P，Q∈Cn×n满足P2Q＝0，PQ＋QP＝0，则（P＋Q）＃存在的充要条件是P＃、Q＃存在，r（P＋Q）＝r（P2＋Q2）＝r（P4＋Q4），此时有：

（P＋Q）＃＝P＃＋ （P＋Q）（Q2）＃ （2）

证明 由条件可知，（P＋Q）＃存在，且P2Q＝－PQP＝QP2＝0。

令P＝R－1，R是非奇异矩阵，P1可逆，P2是幂零矩阵，由P＃存在，可知和存在，且＝0。

Q＝RR－1，由条件知Q1＝0，Q12＝

因为（P＋Q）＃存在，根据秩的关系可知（P2＋Q2）＃存在。根据引理1，可知：

下面只须求出（P2＋Q2）＃即可。

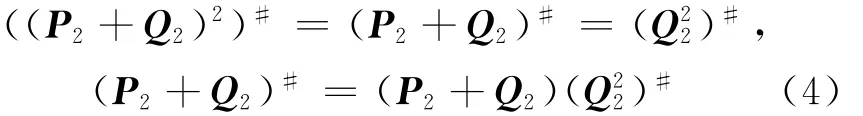
将（4）式代入（3）式中，可得出（P＋Q）＃＝P＃＋（P＋Q）（Q2）＃，得出结论。

性质1 已知P，Q∈Cn×n且P＃、Q＃存在，满足P2Q＝0，QPπ＝0，则有：

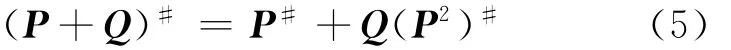
定理2 令N＝，满足：A2B＝0，D2C＝0，BDπ＝0，CAπ＝0。当A＃、D＃存在且r（B）＝r（C）＝r（CB）＝r（BC）时，则有：

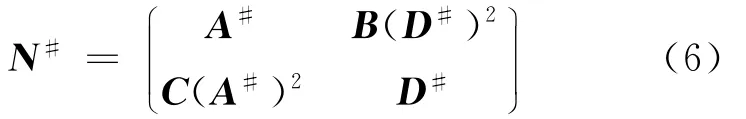
证明 令N＝＝P＋Q，则由条件可知P、Q满足P2Q＝0，QPπ＝0。则根据性质1，N＃＝（P＋Q）＃＝P＃＋Q（P＃）2，可得出结论。

定理3 令N＝，满足：BCA＝0，CBD＝0，A（BC）π＝0，D（CB）π＝0。当A＃、D＃存在且r（B）＝r（C）＝r（CB）＝r（BC）时，有

证明 令N＝＝P＋Q，则据性质1和引理4可得出结论。

3 反三角分块矩阵群逆存在的条件

定理4 令M如（1）式所示，如果AB＝0，CAπ＝0，A是幂等的，则有：

（1）M＃存在当且仅当r（B）＝r（BCB），其中Aπ＝I－A。

（2）如果M＃存在，有

证明 （1）由引理5可知，r（M）＝r（A）＋，而A是幂等的，A＃＝A，A∈A｛1｝，则有：

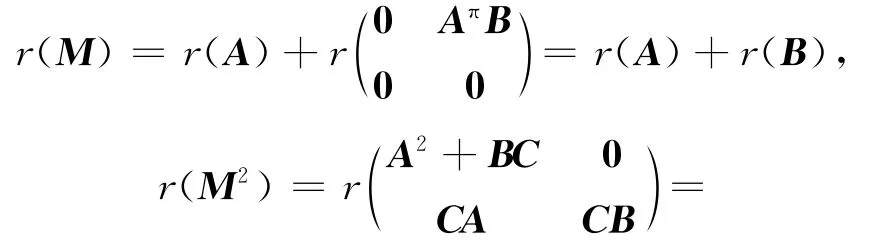
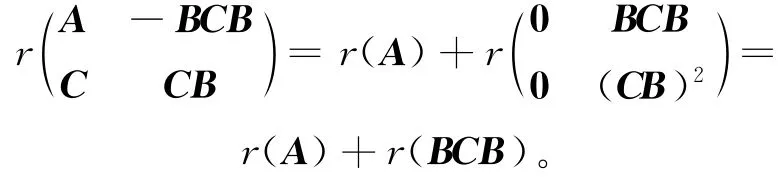
所以M＃存在当且仅当r（B）＝r（BCB）。

（2）令X是（8）式的右半部分，计算可知，

因此X＝M＃，结论得证。

定理5 令M如（1）式所示，其中AB＝0，CAπ＝0，A是幂等的，如果M满足下面2个条件中的任何一个，则M＃存在。

（1）r（AFC，B） ＝r（A）＋r（BCB）－r（C）。

证明 由引理5可知：

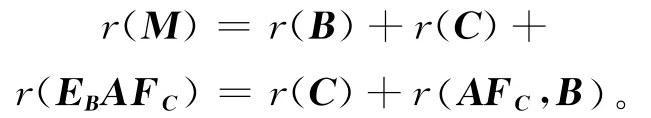
当条件（1）成立时，易知r（M）＝r（M2），则M＃存在。同样根据引理5，可知当条件（2）成立时，M＃存在，就不加详细叙述。

定理6 令M如（1）所示，其中AB＝0，CAπ＝0，A是幂等的，若M满足以下条件：

则M＃存在当且仅当以下4种情况的1个，即

（1）r（B）＝r（BCB）。

（2）r（C）＋r（B）＝r（A）＋r（BCB）。

（3）r（C）＝r（BCB）。

（4）r（A）＋r（BCB）＝r（B）＋r（C）。

证明 由R（B）⊆R（A）可知B1＝EAB＝0，而R（A）⊆R（B），可知EBA＝0。

同理，由R（C＊）⊆R（A＊）可知C1＝CFA＝0，而R（A＊）⊆R（C＊），可知AFC＝0。

所以JD＝EC1SAFB1＝SA。

因为R（B＊）⊆R），即N（SA）⊆N（B），所以由文献［1］中投影原理可知BPL，M＝B，PL，M＝

则SAFB1FJD＝SAFSA＝0，BFB1FJD＝BFSA＝0，所以由引理6可知

另一方面，由R（C）⊆R（SA），可得出r（M）＝r（A，B） ＋r（C）。

接下来的过程结合引理5，即可得出结论。

4 结束语

矩阵的群逆问题是矩阵扰动理论中一个重要的组成部分，本文对于矩阵群逆存在性和表达式进行了研究，特别是分块矩阵群逆的表达式和反三角分块矩阵群逆存在的条件。

［1］ Ben－Israel A，Greville T N E.Generalized inverses：theory and applications［M］.2ed.New York：Springer，2003：152－172.

［2］ Campbell S L，Meyer C D.Generalized inverses of linear transformations［M］.New York：Dover Publications，Inc，1979：120－181.

［3］ 曹重光.体上分块矩阵群逆的某些结果［J］.黑龙江大学学报：自然科学版，2001，18（3）：5－7.

［4］ Bu C.On group inverses of block matrices over skew fields［J］.J.Math，2002，35（4）：49－52.

［5］ Castro－Gonzelez N，Dopazo E.Representations of the Drazin inverse for a class of block matrices［J］.Linear Algebra and its Applications，2005，400：253－269.

［6］ Bu C，Zhao J，Zheng J.Group inverse for a class 2×2 block matrices over skew fields［J］.Applied Mathematics and Computation，2008，204（1）：45－49.

［7］ 周洪玲，王 成，范广慧，等.特殊分块矩阵的群逆的表示［J］.黑龙江工程学院学报：自然科学版，2013，27（1）：78－80.

［8］ 唐 松，吴华璋.块k－循环矩阵的 Moore－Penrose逆和带W权的Drazin逆［J］.合肥工业大学学报：自然科学版，2009，32（9）：1442－1444，1448.

［9］ 左可正，谢 涛.幂等矩阵的组合的可逆性［J］.数学杂志，2009，29（3）：285－288.

［10］ 左可正，谢 涛.两个幂等矩阵的组合的群逆［J］.数学杂志，2014，34：3－5.

［11］ Marsaglia G，Styan G P H.Equalities and inequalities for Ranks of matrices［J］.Linear and Multilinker Algebra，1974，2（3）：269－292.

［12］ 陈永林.关于分块矩阵的g逆的独立性［J］.应用

－数学，1993，6（3）：241－248.