基于NSGA－Ⅱ的层间隔震体系参数优化与能量响应分析

张尚荣， 谭 平， 杜永峰， 包 超， 周福霖

（1.兰州理工大学 防震减灾研究所，甘肃 兰州 730050；2.宁夏大学 土木与水利工程学院，宁夏 银川 750021；3.广州大学 工程抗震研究中心，广东 广州 510405）

层间隔震体系作为一种新型的被动减震控制体系——通过减少地震能量传递到建筑物上的“隔震”和“制振”的被动控制体系［1］，目前在国内外有许多成功的工程应用实例并经历了大地震的考验。层间隔震体系隔震层位置设置不同，会引起结构动力特性的变化，隔震结构的减震机理也会出现新的特征。因此，解决隔震体系参数的优化问题、确定合理的优化目标是分析层间隔震体系的前提。

文献［1］提出以基底剪力最优作为层间隔震体系参数优化的目标，兼顾了隔震层上、下部子结构的性能，具有一定的指导意义；非支配排序遗传算法Ⅱ（NSGA－Ⅱ）［2］作为目前最流行的遗传算法之一，降低了非劣排序遗传算法的复杂性，具有运行速度快、解集的收敛性好并且易于得到全局最优解的优点，成为其他多目标优化算法性能的基准。地震对结构的作用是一种能量的传递、转化和耗散的过程。G.W.Housner在20世纪50年代就曾引入“能量分析”的概念，将能量平衡关系应用于简单的结构设计［3］。文献［4］分析了智能隔震结构的能量响应，以多遇地震的情形为例，分析了线弹性智能隔震体系的瞬时能量传递的解析规律；文献［5］从能量观点出发，引入设计用能量谱的概念，分析了地震输入能量在层间隔震结构中的分配和耗散。

层间隔震体系作为一种新型的结构体系，相关研究仅限于探讨隔震层参数对地震响应及减震效果的影响［6］，对能量的变化规律及相关影响研究尚不明确。

本文基于NSGA－Ⅱ研究了层间隔震体系，以基底剪力最小为优化目标，得到在不同质量比下的层间隔震结构最优频率比和最优阻尼比，从能量角度分析了隔震层在结构不同位置时，层间隔震结构能量分布规律的特征。

1 分析模型和运动方程的建立

在线弹性情况下，两质点层间隔震体系计算模型如图1所示［7］（图中“u”和“s”分别是“upstructure”和“substructure”的缩写，分别表示上、下部子结构）。

图1 层间隔震体系计算模型

其运动方程为：

其中，mup、keq、ceq分别为上部子结构的等效质量、等效水平刚度、等效阻尼；msub、csub、ksub分别为下部子结构的质量、阻尼、水平刚度；¨ug为地面运动加速度。

定义上、下部子结构的自振频率分别为：

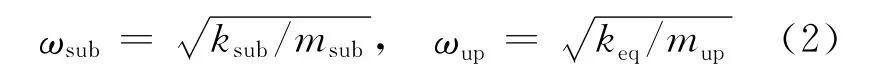
上、下部子结构的阻尼比分别为：

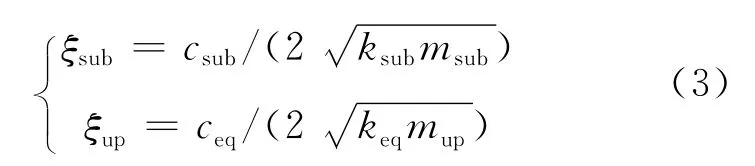
上、下部子结构的质量比为：

上、下部子结构的频率比为：

2 基底剪力方差表示

两质点层间隔震体系模型的基底剪力可表示为：

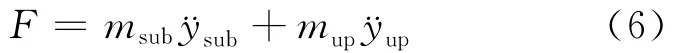
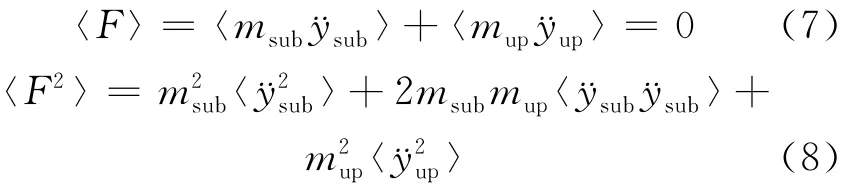
其中，〈·〉表示变量的平均值。设地震激励的功率谱密度函数为（ω），子结构绝对加速度的传递函数为Hy（ω），则子结构加速度响应均方值和乘积的平均值为：

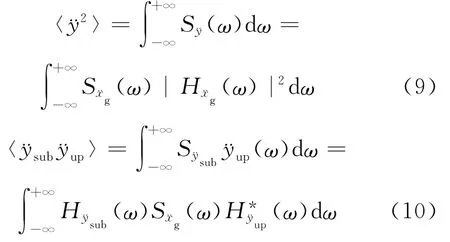
其中，S¨y（ω）为绝对加速度响应的功率谱密度；（ω）为交叉谱密度函数。

展开两质点层间隔震体系运动方程（1）式并分别作Laplace变换，可得各子结构绝对加速度的传递函数如下：

其中

定义两自由度体系的基底剪力功率谱密度函数为SF（ω），可得：

其中，Re［·］为取实部。则基底剪力的方差为：

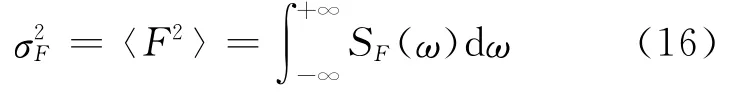
3 参数优化与分析

基底剪力是隔震结构设计中的一个重要指标。随着隔震层刚度和阻尼参数的变化，基底剪力的分布将会随之变化，因此，选取合理的隔震层参数将会对层间隔震体系产生有利影响。本文选取体系的基底剪力最小作为隔震层参数优化目标，采用NSGA－Ⅱ进行优化建模和实现。

3.1 带有精英策略的非支配排序遗传算法

基于多目标NSGA－Ⅱ算法层间隔震结构体系参数优化的流程，如图2所示。算法开始时首先随机产生一个初始群体P0，在此基础上采用二元锦标赛选择、交叉和变异操作产生一个新群体Q0，P0和Q0的群体规模均为N；将Pt和Qt并入到Rt中（初始时t＝0），针对Rt构造其所有的边界集，然后根据需要计算某个边界集中所有个体的聚集距离，并定义偏序集；从偏序集依次选取个体进入Pt＋1，直至Pt＋1的规模为N［8］。

NSGA－Ⅱ在选择过程中，采用非支配排序降低了计算复杂度，加快了收敛速度；形成支配集后引入的精英策略，提高了结果的优化精度与种群水平；此外同时加入的拥挤度处理等方法，保证了种群的分布性与多样性；然后经过交叉变异等操作直到指定最大代数后终止，获得全局最优解集。具体参数优化流程如图2所示。

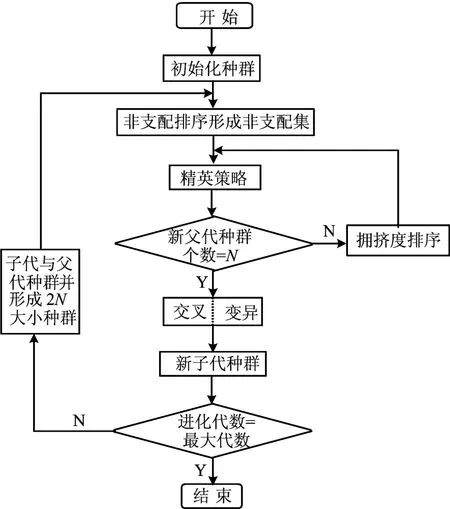
图2 NSGA－Ⅱ参数优化流程图

3.2 参数优化

本文选用结构的总质量为10t，下部子结构阻尼比为0.05，地震动加速度功率谱为白噪声，上、下部子结构的质量比μ变化范围为0.01～20，分析研究以基底剪力最小为优化目标而得到的结构最优频率比和最优阻尼比。

优化过程中选用实值编码方式对2个待优化参数频率比ρ、阻尼比ξup进行编码，在取值范围内随机产生初始种群，设定算法的进化代数为200代，种群大小为100个，种群间的交叉概率为0.9，变异概率为0.1。参数优化表达式为：

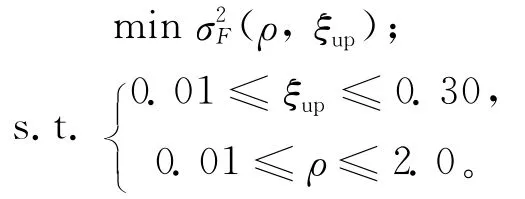
质量比μ＝2.0时NSGA－Ⅱ优化过程如图3所示，可以看出，NSGA－Ⅱ表现出快速的收敛能力，在20代以内已基本得到最优参数，而且20代后保持稳定进入全局最优解。

图3b参数聚集也证实了其在寻优过程中算法的收敛性较好，可以看出其最优值：阻尼比为0.30，频率比为0.164 6。

图3 NSGA－Ⅱ优过程（μ＝2.0）

同理可得在不同质量比下结构最优频率比和最优阻尼比，如图4所示。

通过NSGA－Ⅱ优化分析，结构在不同质量比下的最优频率比和最优阻尼比的结果如图4a所示，随着上、下部子结构质量比增大，上部子结构的最优频率比逐渐减小并收敛于界限值0.01；最优阻尼比逐渐增大并收敛于优化变量界限值0.30。

图4b给出了基底剪力方差的变化情况，随着质量比增大，结构的基底剪力方差趋于一致。

图4 NSGA－Ⅱ计算结果

4 层间隔震体系能量分析

4.1 能量方程

将运动方程（1）式分解为：

在（17）式两边对dusub积分，根据能量平衡原理，可得到结构各部分能量为［9－12］：

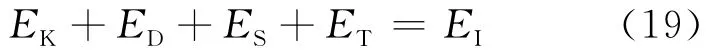
4.2 功率方程

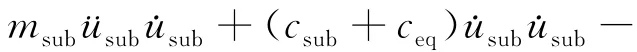
在此定义：PK＝msub¨usubsub为子结构动能功率；PD＝csubsubsub为 子 结 构 阻 尼 耗 能 功 率；PS＝ksubusub˙usub为子结构应变能功率；PT＝ceqsub－up）sub＋keq（usub－uup）sub定义为子结构间转移能功率；PI＝－msub¨ugsub为地震总输入功率。

4.3 能量响应分析

文献［1］研究指出层间隔震体系在不同质量比及对应最优参数下，结构表现出不同的减震机理。基于文献［1］的研究结果，选取满足频率比为ρ＝0.85（μ＝0.1），ρ＝0.165（μ＝2.0），ρ＝0.028（μ＝6.0）对应结构分别作为上部隔震、中间层隔震和下部隔震结构的典型算例（以下分析中以质量比μ分别代表各结构体系），研究其在不同地震激励下结构能量之间的分配和转化。选取3条地震 波 分 别 为 Imperial Valley（1979）－EI Centro Array ＃ 13、Kobe （1995）－Kakogawa 和Northridge（1994）－Arcadia－Campus Dr.作为地震 动 输 入 （以 下 简 记 为 EI－Centro、Kobe、Northridge），其峰值加速度PGA均调整为0.2g（为清晰表现其规律，以下分析中均截取其响应较大时段）。

转移能功率可以理解为单位时间内由下部子结构转移至上部子结构的能量，也可以理解为单位时间内上部子结构对下部子结构所做的功。质量比μ为0.1、2.0、6.0的结构（参数最优）在 EICentro波、Kobe波、Northridge波作用下的转移能功率如图5所示。

由图5可以看出，随着质量比的增大，单位时间内的转移能逐渐减小。质量比μ＝0.1，上部子结构对下部子结构主要做负功，其机理表现为TMD调谐减震；μ＝2.0，上部子结构对下部子结构做功总和为负功，其机理表现为下部子结构部分减震；μ＝6.0，其转移能较小。

结构的转移能随质量比的变化情况如图6所示，可以看出，结构的转移能随质量比的增大表现为先增大后减小的趋势，当质量比较小，在μ≤0.5范围内，转移能存在最大值，结构工作机理相当于TMD调谐系统，通过转移下部子结构的能量，从而减小其运动；μ＞0.5，随质量比的增大，其转移能逐渐减小，当质量比μ≥10.0，转移能较小且为一常数。

算 例 模 型 在 EI－Centro 波、Kobe 波、Northridge波作用下的下部子结构弹性应变能如图7所示。

图5 转移能功率

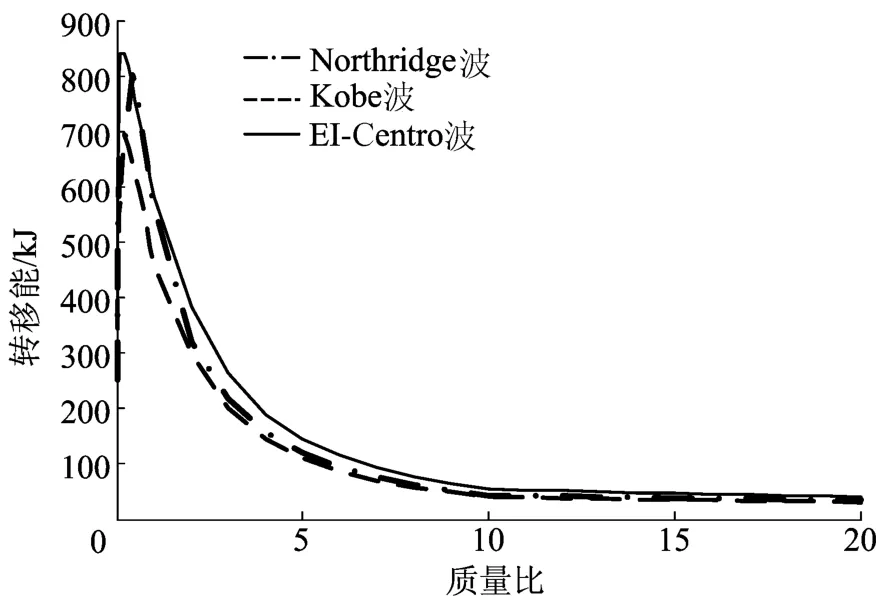
图6 转移能随质量比变化

图7 下部子结构弹性应变能

由图7可以看出，μ＝0.1时，下部子结构弹性应变能最大，μ＝2.0对应下部子结构弹性应变能次之，μ＝6.0对应下部子结构弹性应变能最小。即从选取最优参数的角度可以理解为：层间隔震体系自上部隔震到中间层隔震再到下部隔震，下部子结构的弹性应变能逐渐减小。

算例最优参数模型在EI－Centro波、Kobe波、Northridge波作用下的下部子结构阻尼耗能如图8所示。可以看出，μ＝0.1时，下部子结构阻尼耗能最大，μ＝2.0对应下部子结构阻尼耗能次之，μ＝6.0对应下部子结构阻尼耗能最小；随着质量比的逐渐增大，下部子结构的结构阻尼耗能逐渐减小。即层间隔震体系自上部隔震到中间层隔震再到下部隔震，下部子结构阻尼耗能逐渐减小。

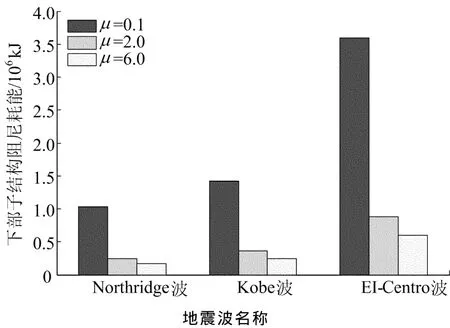
图8 下部子结构阻尼耗能

5 结 论

（1）从转移能功率的角度解释了层间隔震体系转移能的变化规律；当质量比较小时，上部子结构对下部子结构主要做负功，其机理表现为TMD调谐减震；随着质量比的增大，转移能逐渐减小，上部子结构对下部子结构不完全做负功，但做功总和为负功，其机理表现为层间隔震结构对下部子结构部分减震。

（2）层间隔震体系的转移能随质量比的增大先增大后减小，质量比在μ≤0.5范围内，转移能存在最大值，结构工作机理相当于TMD调谐系统，通过转移下部子结构的能量，从而减小其运动；当质量比μ≥10.0，转移能较小且为一常数。

（3）层间隔震体系自上部隔震到中间层隔震再到下部隔震，下部子结构的弹性应变能、阻尼耗能逐渐减小。

［1］ 周福霖，张 颖，谭 平.层间隔震体系的理论研究［J］.土木工程学报，2009，42（8）：1－8.

［2］ Deb K，Aarawal S，Pratap A，et al.A fast elitist non－dominated sorting genetic algorithm for multi－objective optimization：NSGA－II［C］／／Proceeding of the Parallel Problem Solving from Nature.Vol 1，2000：849－858.

［3］ Housner G W.Limit design of structures to resist earthquake［C］／／Proceedings of 1st World Conference on Earthquake Engineering，Berkeley，1956：5.1－5.11.

［4］ 杜永峰，李 慧.智能隔震：基于能量响应和可靠度的前景分析［J］.工程力学，2006，23（Z2）：5－13.

［5］ 张 颖，谭 平，周福霖.层间隔震结构的能量平衡［J］.应用力学学报，2010，27（1）：204－208.

［6］ 金建敏，谭 平，周福霖，等.下部减震层间隔震结构振动台试验研究［J］.振动与冲击，2012，31（6）：104－108.

［7］ 李向真，欧海龙，林 舒.层间隔震结构计算模型的简化分析［J］.地震工程与工程振动，2002，22（1）：121－125.

［8］ 郑金华.多目标进化算法及其应用［M］.北京：科学出版社，2007：21－26.

［9］ 秋山宏.基于能量平衡的建筑结构抗震设计［M］.叶列平，裴星洙，译.北京：清华大学出版社，2010：12－14.

［10］ Soong T T，Dargush G F.结构工程中的被动消能系统［M］.董 平，译.北京：科学出版社，2005：21－23.

［11］ 卜国雄，谭 平，周福霖，等.基于能量法的TMD参数优化设计［J］.华中科技大学学报：城市科学版，2008，25（2）：26－30.

［12］ 常 磊，叶献国，潘文军.基于能量反应谱的结构能量反应竖向分布研究［J］.合肥工业大学学报：自然科学版，2011，34（2）：264－267，291.