模糊离散事件系统时间维度可诊断性分析
佘 维, 杨 慕, 陈 倩, 沈碧波, 叶阳东
(1.郑州大学 软件技术学院,河南 郑州 450003;2.郑州大学 信息工程学院,河南郑州 450052;3.北京大学软件与微电子学院,北京100871)
模糊离散事件系统(fuzzy discrete event sys -tems,FDES)是一类复杂系统的建模分析理论,可为工业系统中的复杂非线性动态行为及相关的不确定性因素提供有效的建模和分析方法。该理论在21世纪初受到人们的广泛关注,文献[1-2]在2001年提出了经典的FDES模型和相关概念,较早的相关研究可追溯至1997年中国国家自然科学基金资助的科研项目“模糊离散事件动态系统的建模理论及应用研究”。
最近10年,FDES的相关研究成为复杂系统理论研究方面最活跃的一支。文献[3]将FDES理论应用于HIV/AIDS治疗系统的研发中,并用于合并异构系统的行为模型;文献[4]将FDES理论应用于移动机器人的行为建模中,根据状态的可观可控性来处理数据的不确定性和环境的动态性;文献[5]将FDES理论与监控系统理论相结合,基于模糊可控性和可观性条件提出了一种模糊监督控制理论框架并将其应用于分散控制监督;文献[6]对事件的可观性进行了深入研究,进一步发展了FDES的诊断理论;文献[7]从事件语言集可控性的角度,对FDES的可观性、分散控制及监控理论进行了大量研究;文献[8]将FDES应用于故障诊断领域,提出了模糊事件时间隶属度的思想;文献[9]将FDES行为模型用于导航控制,根据不精确的传感器数据预测未来的模糊状态,以此控制机器人行走;文献[10-11]对FDES中的时间不确定性问题进行了长期研究,提出了多个与时间因素相关的FDES模型,并将其应用于铁路调度系统和电力系统故障诊断中;文献[12]提出了基于规则的FDES建模方法及自寻优监督控制策略,并在纺织印染控制过程中进行了具体应用;文献[13]对FDES的能控性进行了进一步研究,得到了FDES能控子语言的相关性质及监督控制中的具体实现方法。
观测条件受限是复杂系统中现实存在的一类约束。系统结构的复杂性带来了测量上的困难,传感器采集的系统状态信息可能是不精确的。这种“不精确”不仅说明信息的描述中包含随机性、不完备性和模糊性,还暗示着对其处理时将体现出某种多义性或冲突。因此,在运用FDES理论对复杂系统进行建模分析时必须考虑以下2个关键问题:① 事件的模糊可观程度及其引出的因果关系模糊化;② 复杂的系统结构下,模糊因果关系与不精确的信息相耦合导致系统状态难以辨识和难以诊断。
时间因素作为复杂系统运行、演化过程中的重要属性,对其进行描述、分析和运用一直是FDES研究中的热点[14]。本文针对以上问题,从时间维度寻求系统状态辨识和行为分析的另一方面证据,合并状态和时间信息,并基于不确定性的度量来处理这类问题。
1 FDES时间维度可观性
1.1 时间区间计算方法
定义1 设时间区间tmi=[a,b],tmj=[c,d],并将a、c分别称为tmi、tmj的下界,b、d分别称为tmi、tmj的上界,定义时间区间计算方法。
(1)时间区间的关系运算。

未知时间区间ε与任意tmi的关系定义为:

(2)时间区间的叠加运算为tmi+tmj=[a+c,b+d],令未知时间区间为ε,其与任意区间的叠加运算定义为tmi+ε=tmi。
(3)时间区间的求逆运算为-tmi=[-b,-a],未知时间区间ε求逆后仍为ε。
(4)若tmi⊥tmj∈{γ+,γ-,θ+,θ-},其并集为tmi∪tmj=[e,f],其中e=min(a,c),f=max(b,d),任意tmi∪ε=tmi。
(5)若tmi⊥tmj∈{γ+,γ-,θ+,θ-},其交集为tmi∩tmj=[g,h],其中g=max(a,c),h=min(b,d),任意tmi∩ε=ε。
(6)tmi上、下界的λ度tmj扩展定义为Ex(tmi,tmj,λ)=[a-λ(d-c),b+λ(d-c)],其中λ称为时间区间的扩展程度。
定义2 令ΣF表示一个FDES,e∈E为一模糊事件,状态标识Mi[e>Mj,且状态迁移可在时间区间tmij完成,将此类带有时间约束的状态迁移记为Mi[e▷tmij>Mj。令Mi状态下事件e发生的时间点约束于区间tmi,Mj被观测的时间区间为tmj,定义状态Mi、Mj的时间区间相容程度(time interval compatibility,TIC)为:其中,Ex为tmj的λ度tmij扩展。在带有时间约束的FDES中,某个状态有多于1个的前置状态时,可利用TIC从时间维度分析最有可能的前置状态。
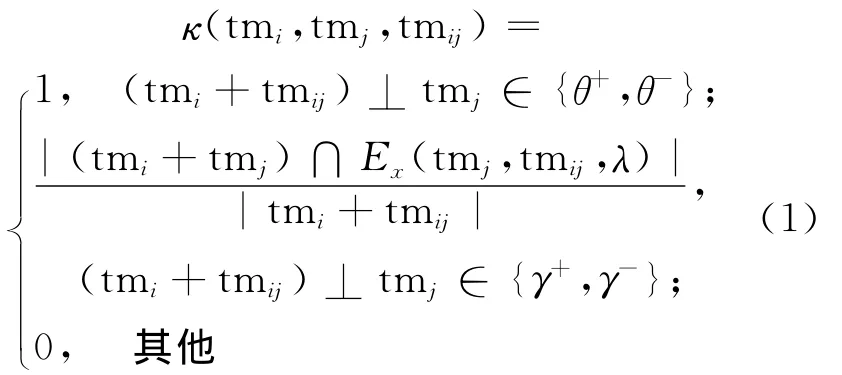
1.2 事件的概率-可能性转化
本文使用贝叶斯条件概率推理来计算FDES中模糊事件发生的概率,并根据文献[15]中的方法将其转化为事件发生的可能性。
贝叶斯网络[16]由一个具有n个节点的有向无环图G和一个与每个节点相关的条件概率表PG构成。G的节点集代表论域U={x1,x2,…,xn}中的变量,U的联合概率分布为:

对于具有m个基本事件{xi1,xi2,…,xim}的随机变量xi,其条件概率为[17]:
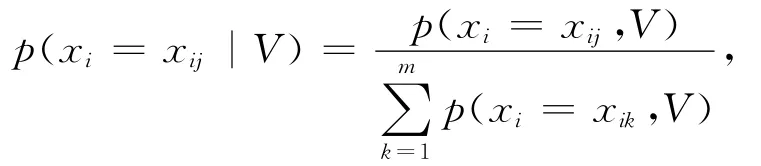
其中,V={x1,…,xi-1,xi+1,…,xn}为观察结果。由此可计算xi=xij的后验概率为[17]:
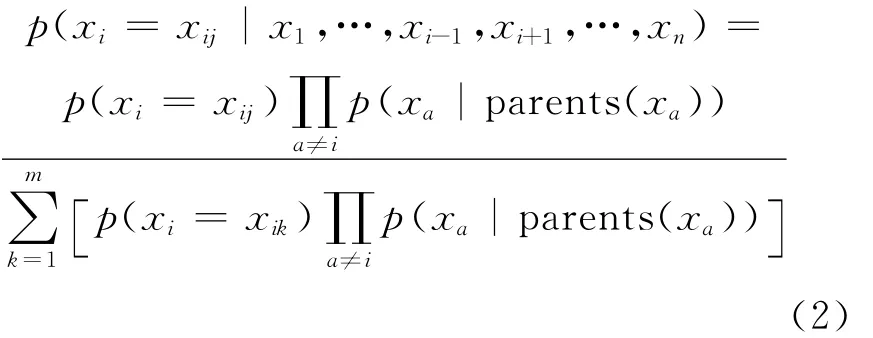
若(2)式中xa的父节点集parents(xa)=∅,则p(xa|parents(xa))=p(xa)。
根据概率-可能性相容原理[18],可将概率分布进行转化得到可能性分布,从量化分析的角度体现为对非精确数据较为客观的处理[19]。本文采用双射法进行概率-可能性的转化[15],令X={xi|i=1,…,n}为论域,且有p(x1)≥p(x2)≥…≥p(xn),则X的可能性分布为:

1.3 时间维度模糊可观程度
FDES中的状态和事件都是具有模糊性的,因此其事件的可观性也是模糊的,既具有部分的可观性,也具有部分不可观性[1]。可观程度de=)描述了FDES中某个模糊事件e的可观性。但是,当事件e的发生难以捕获,而必须以其引发的状态迁移来表征时,则e触发的某个新状态M的出现即成为e发生的重要标志。利用M及其前驱状态·M出现的时间或时间区间可进行e发生时刻的估计,此时e可被感知或推理的程度也由这些存在因果关系的时间区间来计算。
定义3 设ΣTP为一个FDES,其可达状态标识集为R,若M,M′∈R(ΣTP):M[e>M′,则称ΣTP可由Mυ、Mυ′推知e是否发生的能力为ΣTP关于e的时间维度模糊可观性(observability in dimensionality of time,ODT),其中,Mυ、Mυ′分别为M、M′的υ分量。
定义4 设ΣTP为一个FDES,ΣTP的时间约束图TG定义为一个三元组 TG(ΣTP)=(V,Arc,H),其中:①V={Vi|i=1,2,…,n},Vi={(a,b)|a,b∈R:a≤b}为加之于某个si∈S的时间约束,称为TG(ΣTP)的顶点集;②Arc⊆F为TG(ΣTP)的弧集;③H:Arc→2|T|为弧的旁标。
以下给出时间约束图的构造算法。为了简化文字描述,首先约定如下符号标识:对于某个时间 -概率Petri网(time-probability Petri net,TPPN)[11]ΣTP= (S,T;F,E,I,δ,τ,M0),若 有si,sj∈S:∩·sj≠∅,则称sj为si的直接后继库所,记为si→sj,Tij=∩·sj称为si、sj的过程变迁集,τij=max{τ(t)|t∈Tij}称为si、sj过程变迁集的时间区间约束;若有si→sj,sj→sk,…,sl→sm,则称Pos(si)={sj,sk,…,sl,sm}为si的后继库所集。令Vi表示某个库所si上的时间约束,若有si→sj,RS(si,sj)={v+τij|v∈Vi}称为sj在si条件下的时间区间约束。
算法1 TG=get TG(ΣTP)。
输入:ΣTP——时间-概率Petri网TPPN。
输出:TG——ΣTP的时间约束图。
步骤如下:
1.Q:=∅;V:=∅;A:=∅;H:=∅
2. for eachs∈S∧·s=∅do
3. ifMσ-0(s)>0then
4.Q:=Q∪{sk}
5. else
6. 从s→sj开始,依次对s的后继库所进行搜索,找到第1个sk∈Pos(s):Mσ-0(sk)>0,令Q:=Q∪{sk}
7. end if
8. end for
9. for eachs∈Qdo
10.Sq:=Pos(s)∪s
11.As:={(sl,sm)|sl,sm∈Sq∧sm∈Pos(sl)}
12.Hs:{(a,Tslsm)|a∈As}
13.Vs:=∅
14. for eachσ∈Sqdo
15.Vσ={Mv-0(σ)}
16.Vs:=Vs∪{Vσ}
17. end for
18. 从s→sj开始,计算si在s条件下的时间区间约束RS(si,sj),并 将Vi∈Vs更 新 为Vi′=Vi∪RS(si,sj)。对所有sk∈Pos(s)依次进行以上更新操作
19.V:=V∪Vs;A:=A∪As;H:=H∪Hs
20. end for
21. TG=(V,A,H)
22. return TG
定义5 设ΣTP为一个 FDES,TG(ΣTP)=(V,Arc,H)为其时间约束图,事件e∈E的时间维度可观程度(observale degree in dimensionality of time,ODDT)de定义为:
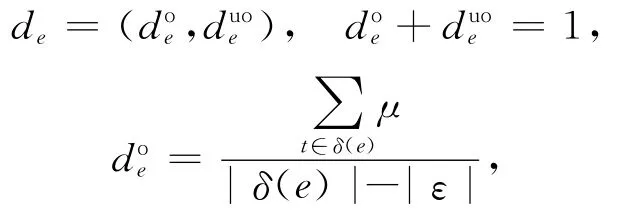
其中,δ为ΣTP中模糊事件e到模糊变迁T的子集的映射;ε为未知时间区间;|ε|为t∈δ(e)中μ=ε的数量。μ的计算方法为:
(1)若有si∈·t,sj∈t·:|Vi|>1∨|Vj|>1,则μ=φ(Vi,Vj,τ(t)),其中

|vi+τ(t)≡vj|为满足vi+τ(t)=vj的时间区间数量;κ以(1)式计算;φ为非己投票函数。
(2)若有si∈·t,sj∈t·:Vi∉V∧Vj∉V,则μ=0。
(3)若有si∈·t,sj∈t·:|Vi|=1∧|Vj|=1,则μ=ε,表示状态未知,不参与的计算。
2 FDES的时间维度可诊断性
系统可诊断性[8]是指:对一个已知的系统进行抽象和建模以后,在一定观测条件下,利用可观的事件序列,可以区分系统中的故障和其他正常行为,或可在不同故障类型之间进行辨识。ODDT是一种观测条件受限时事件可以被感知和推理的程度,通过ODDT分析状态信息中的时间线索,可以为可观程度较低的模糊事件“示踪”,即根据状态信息辨识模糊事件,其分析模型以时间区间计算和可能性理论为基础,对系统实时观测数据进行分析,并由此构造诊断器并分析事件的可诊断程度。
由于FDES中的事件具有模糊性,在表示某个导致故障的事件e时,可采用fe∈[0,1]描述该事件发生的可能性。因此,FDES的故障事件集[6]可 表 示 为Ef= {e∈E:fe>0},并 以f(e1,e2,…,em)=max{fei:=1,2,…,m}计算多个故障事件发生的可能性。与此类似,可将多个事件的 可 观 程 度 扩 为…,m}。为了避免在构建诊断器时事件集为空,引入最大可观事件集[6],即

以时间 -概率 Petri网[11]ΣTP=(S,T;F,E,I,δ,τ,M0)表示FDES,L(ΣF)为其产生的语言,L/η代表L中η的所有后置语言串。对于η∈E*,e∈E,其z投影[5]Pz:E*→E*为Pz(ε)=ε,Pz(ηe)=Pz(η)Pz(e)。Pz的计算方法为:

反向投影函数定义为:
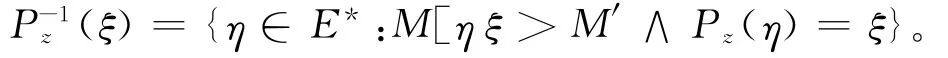
进行z投影的目的是为了将某个串中可观性不大于dzo的事件清除,尤其是对于所有事件均可见或所有事件均不可观的系统,其z投影dzo特化为DES中的投影函数P。
以L≥z表示ΣF语言串中尾事件故障可能性不小于fz的事件集,即

其中,ηl为η的最后一个事件。
定义6 设ΣTP=(S,T;F,E,I,δ,τ,M0)为一个TPPN,Ef为其故障事件集,对于z∈Ef,ΣTP的时间维度可诊断性函数为FDz:E*→[0,1]。当η∈L≥z且ξ∈L/η时,有:

为了构造FDES的诊断器,首先给出可能性故障标识和模糊状态的可观子集的概念,其中可能性故障标识用于标记诊断器的各类状态,而获得模糊状态的可观子集则是构造诊断器状态可达图的先决条件。在此基础上,利用TPPN构造FDES故障诊断器并分析系统的可诊断程度。
令ΣF表示一个FDES,其可能性故障标识[6]为Δz={Fault}∪{Nμ|z,e∈E:(μ=fe)(fe>fz)},其中,Fault为故障发生可能性大于fz的系统状态;Nμ为系统处于故障发生可能性为μ但并未超过fz的状态。
R(M0)的z可观子集Rz定义为:

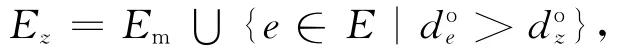
其中,Mi,Mj∈R(M0)。关于z的故障诊断器可由ΣF的可达图构造为:
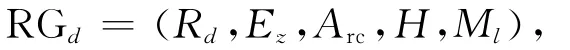
其中,状态空间Rd⊆2Rz×Δz,包括以Ml为初始状态的所有可达状态;某个状态Ml′={(Mi,li)},Mi∈Rz,li∈Δz,初始状态Ml={(M0,N0)},说明在初始时ΣF处于正常状态;Arc为弧集;H为弧的旁标。
标记蔓延函数[6]用于描述从诊断器RGd状态转移时的标记变化,即
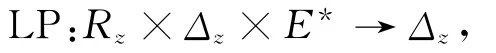
对Mi∈Rz,li∈Δz,若l=Fault,则 LP(Mi,l,η)=Fault;若l=Nμ且fη>fz,则 LP(Mi,l,η)=Fault;若l=Nμ,fη<fz且fη>μ,则 LP(Mi,l,η)=Nfη;若l=Nμ,fη<fz且fη<μ,则LP(Mi,l,η)=Nμ。
诊断器RGd的事件触发将引起状态的迁移。若Ml′∈Rd,e∈Ez,Ml′[e>Ml″,则

其中,Lz为所有以e∈Ez结束的串。
3 FDES可诊断性算例分析
本文以电力系统运行设备的故障诊断为例,运用时间维度可诊断性分析方法处理观测数据并构造诊断器。
3.1 故障诊断原理
电力系统运行设备“母线”的保护装置布局图如图1所示,其中“母线”标为B1,与其直接相关的保护装置为“断路器”CB2及CB5,一旦B1出现电压过高等危险指标,其保护装置的控制器B1m立即工作,使得CB2及CB5断开,以切断B1与其他运行设备的电路联系。若B1m自身出现故障,或者CB2、CB5中任一装置发生故障未能断开,B1的远端保护装置L1Ss则在一定时间延迟后工作,使得远端的CB1断路器断开[20]。
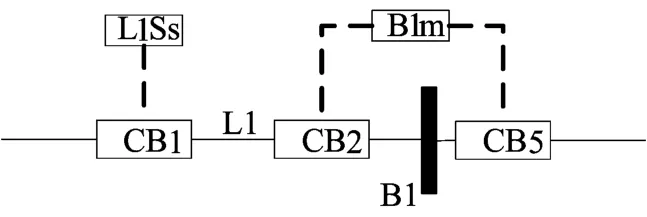
图1 运行设备及其保护装置布局图
状态的时序特征如图2所示。图2中s0~s5分别表示B1、B1m、CB2、CB5、L1Ss、CB1,令e1~e4分别表示“母线B1引发B1m动作”、“B1m控制器指示所属断路器CB2、CB5打开”、“L1Ss产生动作”、“L1Ss指示所属断路器CB1打开”。
算例1 令图2中t0~t5分别描述状态分量s0~s5最早可能出现的时刻,τ1~τ5分别为s0→s1、s1→s2、s1→s3、s0→s4、s4→s5的时延区间,其中s0→s1即为s0状态引发s1状态的过程。τ1~τ5分别为:τ1=[10,40],τ2=τ3=τ5=[20,40],τ4=[510,540]。s0~s5的因果关系为:s0→s1;s1→s2其中为si状态未出现。
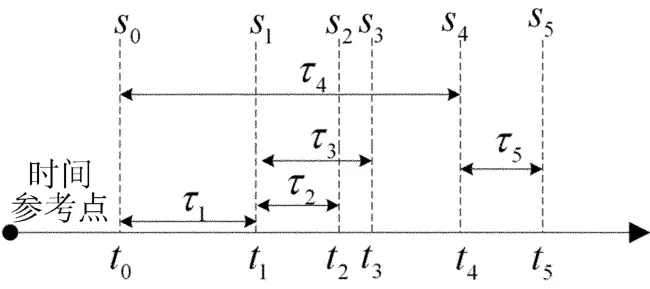
图2 状态的时序特征
设s0~s5中的因果关系的先验概率和条件概率为:p(s0)=0.58%,p(s1)=96.98%,p(s4)=0.07%。
设观测所得各状态分量的信息为:O(s3)=87,O(s4)=550,O(s5)=596,其中O(si)为最早观测到si状态分量的时间。求取s0状态分量代表的概念为“真”的可能性。
3.2 状态的时序特征及其建模
根据3.1所述原理,s0~s5因果关系中的概率分布可作为相应的可能性分布参与分析和计算。基于以上关系和参数,对s0构建其状态蔓延的 TPPN模型ΣTP=(S,T;F,E,I,δ,τ,M0)以求取s0状态存在的可能性,如图3所示。
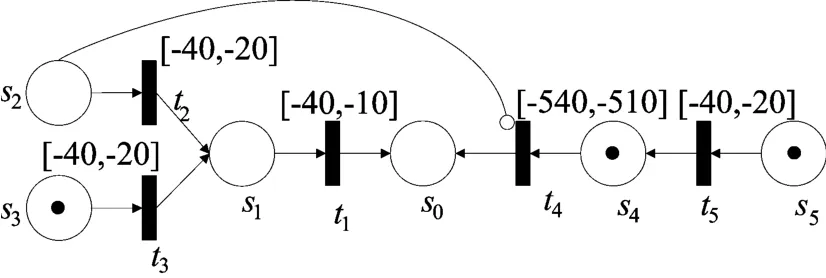
图3 状态蔓延的TPPN
(1)S={s0,s1,s2,s3,s4,s5}。
(2)T={t1,t2,t3,t4,t5}。
(3)F={(t1,s0),(s1,t1),(t2,s1),(t3,s1),(s2,t2),(s3,t3),(t4,s2),(t4,s0),(s4,t4),(t5,s4),(s5,t5)}。
(4)E={e1,e2,e3,e4}。
(5)I={(s2,t4)}。
(6)δ(e1)=Te1={t1},δ(e2)=Te2={t2,t3},δ(e3)=Te3={t4},δ(e4)=Te4={t5}。
(7)τ(t1)=[-40,-10],τ(t2)=τ(t3)=τ(t5)=[-40,-20],τ(t4)=[-540,-510]。
(8)令M0=(Mσ-0,Mυ-0),其中Mσ-0=[0,0,0,1,1,1],Mυ-0={ε,ε,ε,[87,87],[550,550],[596,596]}。
(9)输出矩阵的转置(A+)T及输入矩阵的转置(A-)T可根据图6构造。
(10)根据s0~s8中的因果关系的先验概率和条件概率,可构造事件触发矩阵,以p(s0|s1)为例说明计算过程,即

同理,p(s1|s2)=p(s1|s3)=0.999 8,p(s4|s5)=0.998 3,p(s0|s4)=0.717 1。由 max{pi}=0.999 8,可由(3)式转化为相应的可能性。由此构造e1~e4的事件触发矩阵Be1~Be4,为了简化描述仅给出不为0的元素:Be1(t1,s0)=0.904 3,Be2(t2,s1)=Be2(t3,s1)=1,Be3(t4,s0)=0.717 2,Be3(t5,s4)=0.998 5。
(11)时间区间回溯矩阵与具体的状态标识有关,当有新的状态产生时相应的时间区间回溯矩阵也需重新计算。
3.3 基于ODDT的可诊断性分析
首先构造算例1中TPPN的时间约束图,如图4所示,根据图4计算各事件的ODDT。为了处理某些时标有误差的观测数据,令时间区间扩展程度λ=0.5,各事件的ODDT见表1所列。
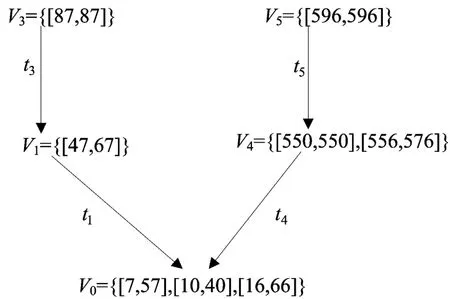
图4 TPPN的时间约束图

令Ef={e1,e2},并分别构造其诊断器。

表1 事件的时间维度可观程度
(1)对于e1,其诊断器为 RGd-1=(Rd,Ez,Arc,H,Ml),如图5所示,诊断器事件集为Ez={e1},诊断器状态为:Ml-0={(M4,N0)},Ml-1={(M3,Fault),(M7,Fault)}。

图5 基于ODDT的诊断器1
(2)对于e2,其诊断器为 RGd-2,如图6所示,诊断器的事件集为Ez={e1,e3,e4},e∈E,诊断器状态为:Ml-0={(M4,N0)},Ml-1={(M3,Fault)},Ml-2= {(M9,N0.0023)},Ml-3= {(M6,Fault),(M1,Fault)},Ml-4={(M10,N0.0048),(M8,N0.0048)},Ml-5= {(M5,Fault),(M0,Fault)},Ml-6={(M7,Fault)}。
在RGd-1和RGd-2所有状态中均不存在关于F的不确定性环路。因此RGd-1为e1完全可诊断,RGd-2为e2完全可诊断,可诊断程度均为1。
3.4 方法对比及分析
为了说明基于ODDT的可诊断性分析在FDES故障诊断中的优势,使用文献[6]中基于观测事件链及其可观性的方法对同一数据集进行分析并比较其差异。

图6 基于ODDT的诊断器2
由于在算例1的ΣTP模型中t1、t2所引发的状态改变不可见,即e1为不可观事件,e2为部分可见事件(t3引发的改变可见,而t2引发的改变不可观),可将故障蔓延过程中s1、s2中发生的状态改变视为通过某些不可观事件的发生而到达的不可观可达态中的分量变化。根据文献[6]中的方法,将各事件的可观程度量化,见表2所列。

表2 文献[6]方法计算的事件可观程度
根据fe1=0.030 8,fe2=0.013 1,fe3=0.002 3,fe4=0.004 8,Ef={e1,e2},分别构造其诊断器:
(1)对于e1,其诊断器 RGd-1=(Rd,Ez,Arc,H,Ml),如图7所示。
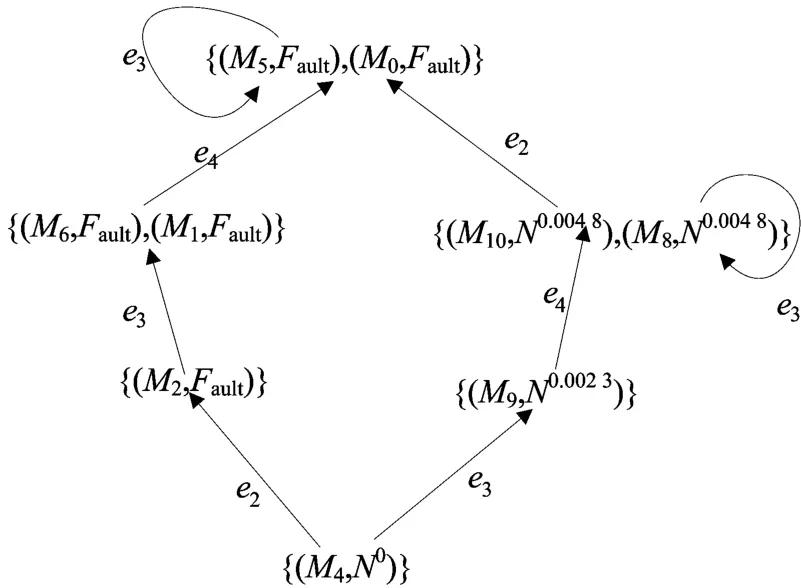
图7 关于算例1的诊断器1
诊断器的事件集为Ez=(e2,e3,e4),诊断器状态 为:Ml-0= {(M4,N0)},Ml-1= {(M2,Fault)},Ml-2= {(M9,N0.0023)},Ml-3= {(M6,Fault),(M1,Fault)},Ml-4={(M10,N0.0048),(M8,N0.0048)},Ml-5={(M5,Fault),(M0,Fault)}
(2)对于e2,其诊断器为 RGd-2,如图8所示,诊断器的事件集为Ez={e3,e4},诊断器状态为:Ml-0={(M4,N0)},Ml-1={(M1,Fault),(M6,Fault),(M9,N0.0023)},Ml-2={(M0,Fault),(M5,Fault),(M8,N0.0048),(M10,N0.0048)}。

图8 关于算例1的诊断器2
图8中存在1个0.004 8和F之间的不确定环路,则关于e2的诊断器RGd-2的可诊断程度为:

因此可认为若e1发生时出现故障,可由相关因果关系明确判断其原因;而e2发生时若存在故障,由其相关规则进行故障诊断得出结论的可能性为0.366 4。
文献[6]中的方法根据离散事件的可观程度及其故障可能性构造故障诊断器,以此来分析事件的可诊断程度。但由于事件的可观程度仅由观测获得,没有利用状态之中蕴含的其他相关信息,当时间可观程度降低时,其可诊断程度也随之下降。因此分析结果中e2为部分可诊断,其可诊断程度仅达到0.366 4。
本文方法则采用ODDT计算事件的时间可观程度,充分利用隐含信息构造诊断器。由于ODDT是一种从时间层面解释状态信息的指标,其计算过程以时间约束图的分析为基础,以状态信息中的时间区间相容性表达状态间隐含的因果关系和时间线索。以ODDT构造的诊断器将这些可见与隐含的信息均表达于同一框架下,提高了系统的可诊断程度。对比文献[6]的诊断器构造方法可知,在基于ODDT的可诊断分析的方法中,e2的可诊断程度明显提高。
4 结束语
本文针对观测条件受限时的模糊离散事件系统故障诊断问题进行了深入分析,提出了FDES中离散事件在时间维度上的模糊可观性概念及相应可观程度(ODDT)的度量方法。该方法通过构造观测信息的时间约束图,以全局状态的时间信息为基础,采用时间证据合并的方法分析离散事件在时间维度上的可观性,通过一种非己投票函数计算事件的ODDT,进而运用于FDES故障诊断器的构造。根据ODDT分析系统状态,可在观测条件受限以致事件难以捕获的情况下,利用状态信息所含的时间线索辨识模糊事件并发现系统隐患。实例分析表明,与单纯依赖故障事件链分析的诊断方法相比,根据ODDT构造的诊断器提高了系统的可诊断程度。
[1] Lin F,Ying H.Fuzzy discrete event systems and their observability[C]//Proceedings of the Joint 9th IFSA World Congress and 20th NAFIPS International Conference.IEEE,2001:1271-1276.
[2] 叶阳东,贾利民.模糊离散事件动态系统的研究[C]//2001年中国智能自动化会议论文集:上册.中国自动化学会,2001:358-364.
[3] Ying H,Lin F,Luan X,et al.A fuzzy discrete event system for HIV/AIDS treatment planning[C]//Proceedings of the 2004IEEE International Conference on Fuzzy Systems.IEEE,2004:197-202.
[4] Huq R,Mann G K I,Gosine R G.Behavior-modulation technique in mobile robotics using fuzzy discrete event system[J].IEEE Transactions on Robotics,2006,22(5):903-916.
[5] Qiu D,Liu F.Fuzzy discrete-event systems under fuzzy observability and a test algorithm[J].IEEE Transactions on Fuzzy Systems,2009,17(3):578-589.
[6] Liu F,Qiu D.Diagnosability of fuzzy discrete-event systems:a fuzzy approach[J].IEEE Transactions on Fuzzy Systems,2009,17(2):372-384.
[7] Cao Y,Ying M,Chen G.State-based control of fuzzy dis-crete-event systems[J].IEEE Transactions on Systems,Man,and Cybernetics,Part B:Cybernetics,2007,37(2):410-424.
[8] Kilic E.Diagnosability of fuzzy discrete event systems[J].Information Sciences,2008,178(3):858-870.
[9] Schmidt K W,Boutalis Y S.Fuzzy discrete event systems for multiobjective control:framework and application to mobile robot navigation[J].IEEE Transactions on Fuzzy Systems,2012,20(5):910-922.
[10] She W,Ye Y.Fault diagnosis via fuzzy time analysis[C]//International Conference on Fuzzy Systems.New York:IEEE,2012:1-7.
[11] 佘 维,宋 伟,叶阳东.因果链解耦的时间-概率模型[J].计算机集成制造系统,2013,19(10):2536-2549.
[12] 张 颖,邵世煌.基于规则的模糊离散事件系统建模与控制研究[J].控制与决策,2006,21(11):1257-1263.
[13] 杨 文.模糊离散事件系统监督控制理论[J].自动化学报,2008,34(4):460-465.
[14] Akramizadeh A,Akbarzadeh T M R,Khademi M.Fuzzy discrete event system modeling and temporal fuzzy reasoning in urban traffic control[C]//Proceedings of the Intelligent Automation and Control Trends,Principles,and Applications.TSI Press,2004:181-186.
[15] Dubois D,Prade H.Unfair coins and necessity measurements:towards a possibilistic interpretation of histograms[J].Fuzzy Sets and Systems,1983,10(1):15-20.
[16] Song I J,Cho S B.Bayesian and behavior networks for context-adaptive user interface in a ubiquitous home environment[J].Expert Systems with Applications,2013,40(5):1827-1838.
[17] 吴 欣,郭创新,曹一家.基于贝叶斯网络及信息时序属性的电力系统故障诊断方法[J].中国电机工程学报,2005,25(13):14-18.
[18] 毕 翔,韩江洪,王跃飞,等.面向PLC的离散事件控制系统设计方法研究[J].合肥工业大学学报:自然科学版,2010,33(9):1333-1337.
[19] Dubois D,Foulloy L,Mauri S G,et al.Probability-possibility transformations,triangular fuzzy sets,and probabilistic inequalities[J].Reliable Computing,2004,10 (4):273-297.
[20] 康泰峰,吴文传,张伯明,等.基于时间溯因推理的电网诊断报 警 方 法 [J].中 国 电 机 工 程 学 报,2010,30(19):84-90.

