基于改进的LMD和GRNN组合风速预测
雷庆坤, 李生虎, 陈曦鸣, 王艳艳, 华玉婷
(1.合肥工业大学 电气与自动化工程学院,安徽 合肥 230009;2.安徽省电力公司,安徽 合肥 230061)
风速的波动性和间歇性使风电并网对电力系统的安全、经济、稳定运行产生严重影响[1]。因此,风速的准确预测具有重大意义。
目前常用的风速预测方法一般是基于历史数据的统计预测方法,包括持续法[2]、卡尔曼滤波法[3]、时间序列法[4-5]、支持向量机[6-7]、神经网络法[8-9]等。其中,持续法直接取上一点的观测值作为预测值,误差较大;卡尔曼滤波法需假定已知噪声的统计特性,而风速噪声难以估计;时间序列法存在低阶模型预测精度低、高阶模型参数估计难的问题;支持向量机建模过度依赖核函数及其参数的 选 择;广 义 回 归 神 经 网 络[10-11](generalized regression neural network,GRNN)是一种局部逼近网络,具有良好的非线性映射能力,与传统神经网络相比,GRNN只需调整光滑因子1个参数,网络模拟效果好、计算速度快、结果稳定,比较适合于预测具有非线性和非平稳性的风速序列。但其实质仍是直接拟合风速数据的“黑箱”模型,虽有一定的效果,但忽略了风速本身特性。所以使用GRNN预测风速前需对风速数据预处理,深度挖掘风速特性,即将风速序列根据不同的特征信息分解开来,分别进行预测。
目前风速分解的方法有小波分析[12]、经验模式 分 解 (empirical mode decomposition,EMD)[13]、局域均值分解(local mean decomposition,LMD)[14]等,其中小波分析具有良好的时频局域化特性,但分解效果取决于基函数的选择,自适应性差;EMD自适应强,但存在端点效应和过包络等问题[15];LMD在获取PF分量的迭代过程中采用除法运算,而EMD采用减法,LMD的迭代次数明显较少,端点效应较轻[16-17]。但若滑动跨度选择不当,会引起函数不收敛,导致过平滑,影响算法精确度。
针对LMD因过平滑而导致分解精度较低,文献[18]提出采用三次样条插值法改进,分解精度得到提高,但三次样条插值属全局插值,确定任一小区间上的三次多项式时,考虑了全部数据点对它的影响,不仅扩大误差传播范围,还增加计算量。实际上利用部分连续的数据点即可描绘出一段曲线的形状。
Akima插值法是一种具有一阶光滑性的局部插值法[19],其分段三次多项式仅利用较少的局部数据点,即使采样点较稀疏,插值曲线也不易出现摇摆,具有较好的保形性和抗扰性。
本文针对风速的非线性和非平稳性,提出一种基于LMD和GRNN的组合风速预测模型。鉴于LMD中滑动平均法引起的过平滑现象,提出采用Akima插值法对上、下极值点分别插值拟合得到上、下包络线,进而求出局部均值函数和局部包络函数的方法,对LMD做出改进。首先将改进后的LMD算法用于风速分解,得到不同频率的风速分量;然后运用GRNN神经网络对各分解分量分别建模预测;最后将各预测结果叠加得出最终风速预测值。
1 Akima插值的改进LMD算法
1.1 Akima插值原理
设平面上n个不等距结点(xi,yi)(i=0,1,…,n-1),其中x0<x1<…<xn-1,相应的函数值为yi=f(xi)。要构造一条满足yi=f(xi)的光滑曲线y=f(x),可首先用Akima方法来构造指定子区间上的三次插值多项式。若在子区间[xk,xk+1](k=0,1,…,n-2)上的2个端点处满足以下4个条件:
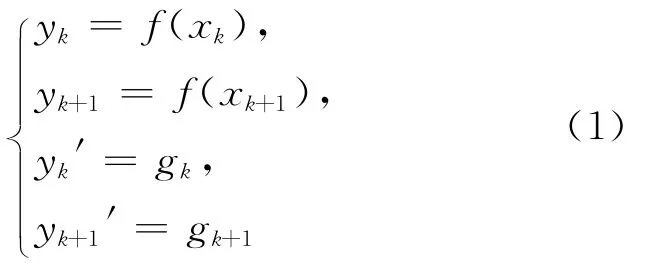
则在此区间上可以唯一确定一个三次多项式:
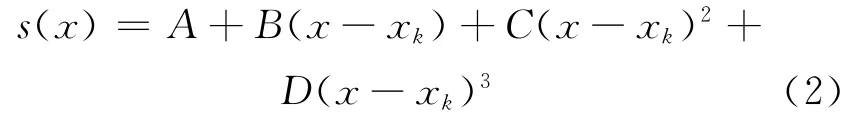
根据(2)式计算该子区间上各个插值点的函数值,而该多项式的系数求法如下所述。
根据Akima提出的用5个数据点来估计出中间点导数的几何条件,可由(3)式、(4)式计算gk和gk+1:
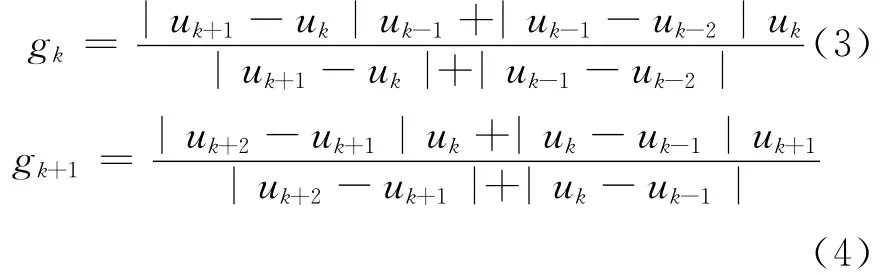
当uk+1=uk与uk-1=uk-2时
当uk+2=uk+1与uk=uk-1时,有
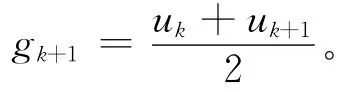

最后,可以求得在子区间[xk,xk+1]上的三次多项式的系数为:
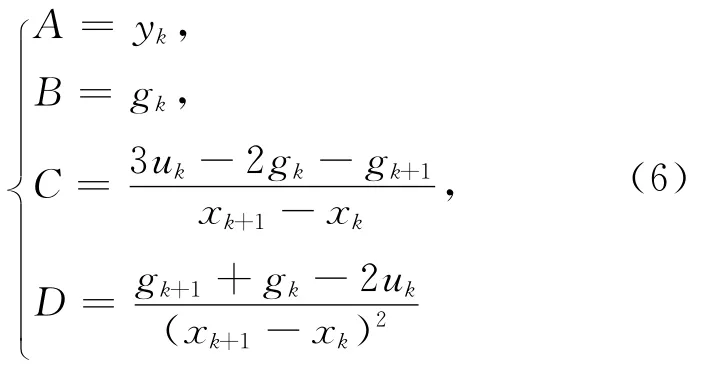
应用上述插值方法,就可对数据序列进行插值拟合。
1.2 LMD 算法
LMD将非平稳信号分解为若干PF分量和残余分量。每个PF由一个包络信号和一个纯调频信号相乘组成。具体方法如下:
(1)找出原始信号所有的局部极值点ni,求出所有相邻局部极值点的平均值mi和包络估计值ai,即
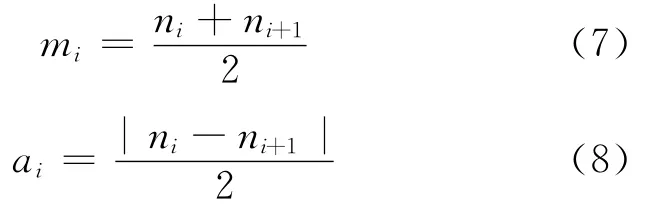
(2)采用滑动平均法平滑mi序列和ai序列,求取局部均值函数m11(t)和包络估计函数a11(t)。
(3)从原始信号x(t)中分离m11(t),再用所得结果除以a11(t),即
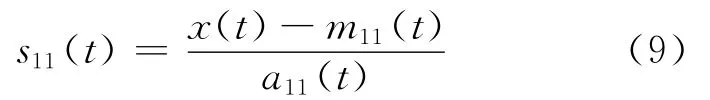
判断s11(t)是否为纯调频信号,若不是,将s11(t)作为新的原始信号重复步骤(1)~ (3),迭代n次,直至s1n(t)为纯调频信号,即其包络估计函数a1(n+1)(t)=1。实际应用中,为减少迭代次数,可用a1n(t)≈1作为迭代终止条件。
(4)把迭代过程中产生的所有包络估计函数相乘便得到包络信号(瞬时幅值函数),即
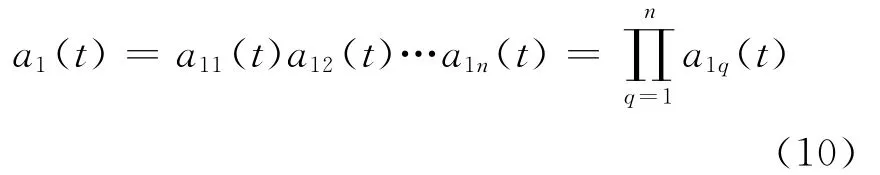
(5)将a1(t)和s1n(t)相乘便可以得到原始信号的第1个PF分量:
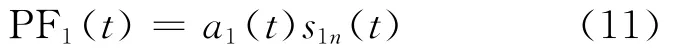
(6)从原始信号中分离 PF1(t),得到信号u1(t),重复以上步骤(1)~ (5),循环k次,直到uk(t)为一单调函数为止。至此,原始信号x(t)被分解为一系列PF分量和一个单调函数uk(t)之和,即
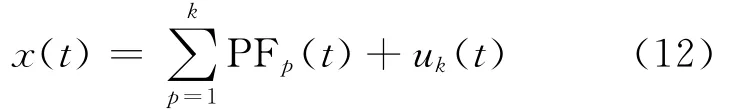
1.3 改进的LMD算法
基于Akima插值的LMD算法与传统LMD算法在求取局域均值函数和局域包络函数上不同,其他步骤相同。主要步骤如下:
(1)分别计算信号的极大值点集maxi(i=1,2,…,M),极小值点集 mini(i=1,2,…,N)。
(2)采用Akima插值法,即利用(2)式和(6)式对极大值点集插值拟合得到包络线Emax(t),对极小值点集插值拟合得到包络线Emin(t)。
(3)由包络线Emax(t)和Emin(t)得到局域均值函数m11(t)和局域包络函数a11(t),其计算公式为:
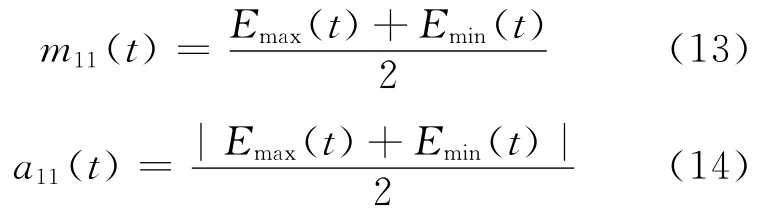
相比于传统LMD,该算法不需重复计算,且其误差较小,故在计算效率和精确度上有较大的优势。
1.4 LMD分解效果的评价指标
为比较改进的LMD和传统LMD的分解效果,引入文献[20]提出的基于能量的评价指标θ。LMD分解可能产生虚假成分,导致各PF的能量改变,可通过比较LMD分解前后的信号能量来评估分解效果。理论上θ越大,分解效果越差。
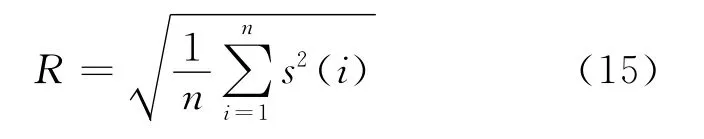
其中,s(i)为待计算有效值的信号;n为采样点数。
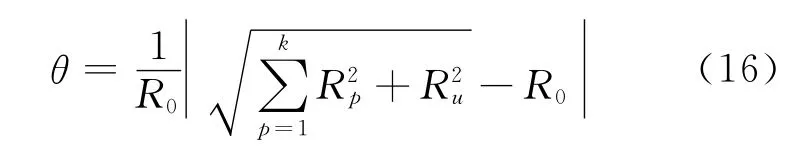
其中,k为LMD分解得到的PF个数;R0为原信号有效值;Rp为第p个分量有效值;Ru为残余量有效值。
2 LMD-GRNN 组合预测模型
2.1 GRNN 原理
GRNN神经网络理论基础是非线性回归分析,非独立变量相对于独立变量的回归分析实际上是计算具有最大概率值的非独立变量。设随机向量x和随机变量y的联合概率密度函数为f(x,y),x的维数为p,已知x的观测值为X0={X01,X02,…,X0p},则y相对于X0的回归,也即条件均值为:即为在输入为X0的条件下Y的预测输出。应用Parzen非参数估计,可由样本数据集{Xi,,其中Xi={Xi1,Xi2,…,Xip},估算密度函数(X0,y)为:
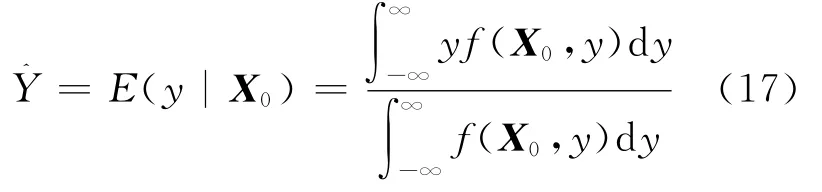
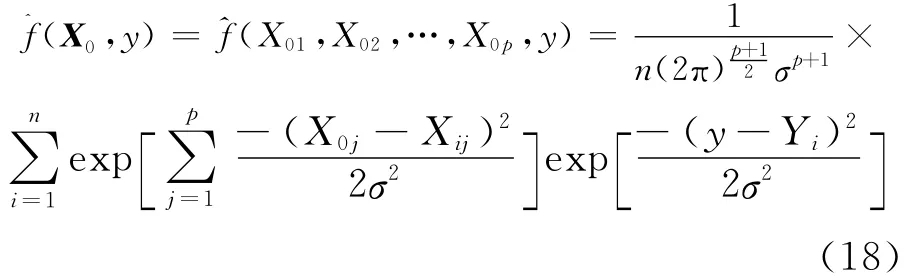
其中,n为样本容量;σ为高斯函数的宽度系数,称为光滑因子。用(X0,y)代替f(X0,y)代入(17)式中,交换积分与求和顺序即可求出
当σ取值非常大时,估计值近似等于所有样本因变量的均值;相反,当σ趋于0时,估计值和训练样本非常接近,当待预测点被包含在训练样本集中时,预测值会和样本中对应的因变量非常接近,而一旦碰到样本未能包含的点,预测效果可能非常差,这种现象称为过拟合。所以需要选择合适的光滑因子σ。
当σ取值非常大时,估计值近似等于所有样本因变量的均值;相反,当σ趋于0时,估计值和训练样本非常接近,当待预测点被包含在训练样本集中时,预测值会和样本中对应的因变量非常接近,而一旦碰到样本未能包含的点,预测效果可能非常差,这种现象称为过拟合。所以需要选择合适的光滑因子σ。
2.2 预测模型的建立
将改进的LMD和GRNN相结合,建立一个新的预测模型。预测步骤如下:
(1)使用改进的LMD方法分解风速序列,得到相对平稳的不同频带的分量PFi和余量uk。
(2)对不同频带的分量PFi和余量uk,分别建立相应的GRNN预测模型。
(3)将各预测值叠加,得到最终风速预测值。具体流程如图1所示。
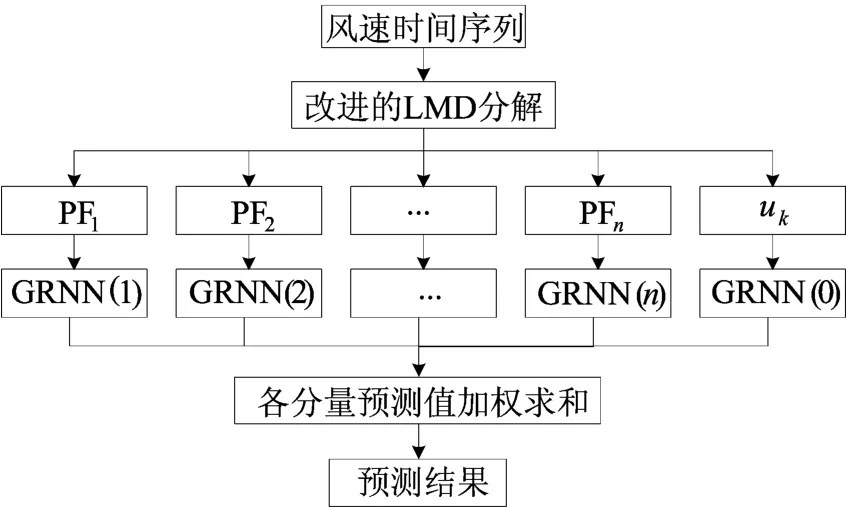
图1 改进的LMD-GRNN组合预测模型
2.3 误差指标
采用平均相对误差ARE(average relative error)及均方根误差 RMSE(root-mean-square error)2项作为风速预测指标,其定义为:
其中,y(k)为第k个样本的实测值;yd(k)为第k个样本的预测值;N0为样本容量。
3 算例分析
以某风电场2010年1月1日到2月4日共35d连续840h的实测小时风速数据为例。利用前720个数据作为模型训练数据,后120个数据作为模型测试数据。
3.1 数据预处理
首先用Akima插值改进的LMD对风速数据进行分解,分解结果如图2所示。为了对比研究,再分别用传统LMD和三次样条改进的LMD分解风速,结果如图3、图4所示。图3中,X(t)分量为原始风速信号。
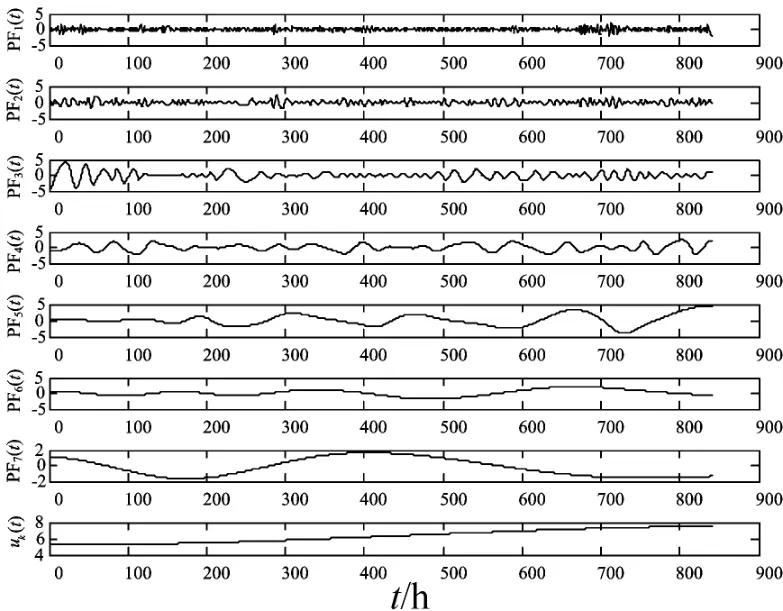
图2 Akima改进的LMD分解结果

图3 传统LMD分解结果
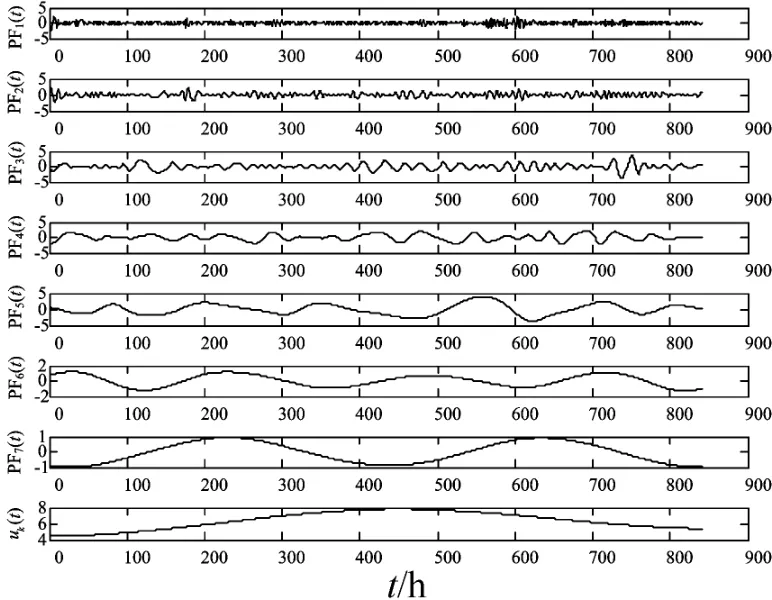
图4 三次样条改进的LMD分解结果
由图2可知,从分解后的分量特征可看到PF分量依次从较高的频率到较低频率,这代表了风速数据的短期波动特征。PF1和PF2为没有明显变化规律的高频分量,一般认为是风速的随机影响部分;一些较低频率的PF分量还具有较强的正弦波动特点,可认为是风速的周期性分量;最后的残余项就是风速的趋势项,代表风速的基本部分,它可以很清楚地显示出风速的长期走势。
比较图2、图3、图4,从高频分量看,Akima改进的LMD和三次样条改进的LMD获得的高频分量其幅值波动都较小,说明高频部分比传统LMD分解更彻底,频带较少混叠;从残余量看,Akima改进的LMD的残余量明显比三次样条改进的LMD和传统LMD的残余量波动程度较小,更接近于理论上的单调趋势项,所以Akima改进的LMD分解更精确,较好地克服了LMD因过平滑而引起的分解精度较低的缺点。
为了更直观地比较上述3种方法的分解效果,可以考察θ评价指标,见表1所列。

表1 3种算法分解效果比较
由表1可知,相比于传统LMD和三次样条改进的LMD,Akima改进后的LMD的θ指标明显减小,说明经Akima插值改进后的LMD分解更彻底、更精确。
3.2 预测模型的建立及参数确定
针对改进的LMD分解后的各PF分量和余量uk的特点,选择合适的光滑因子σ分别建立GRNN预测模型,最后将各预测值叠加得到最终风速预测值。本文采用交叉验证方法训练GRNN网络,为找出最优的σ值,设置σ∈[0.05,10],初始值σ=0.05,以0.01为步长,以预测值平均相对误差最小为目标,循环找出最优的σ值。各分量建立的GRNN模型σ参数寻优结果见表2所列。

表2 各分量GRNN模型参数
3.3 预测结果分析
为了说明改进的LMD-GRNN模型有效性,将其与GRNN模型、LMD-GRNN模型进行比较。预测结果比较如图5所示,相对误差比较如图6所示。
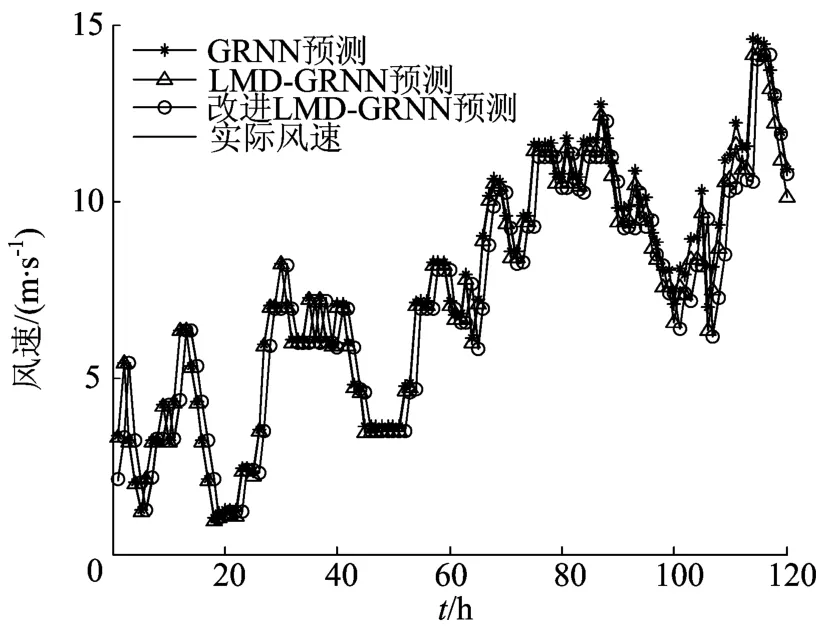
图5 几种模型风速预测结果

图6 几种模型的相对误差比较结果
利用误差指标ARE和RMSE对3种模型进行评定,见表3所列。
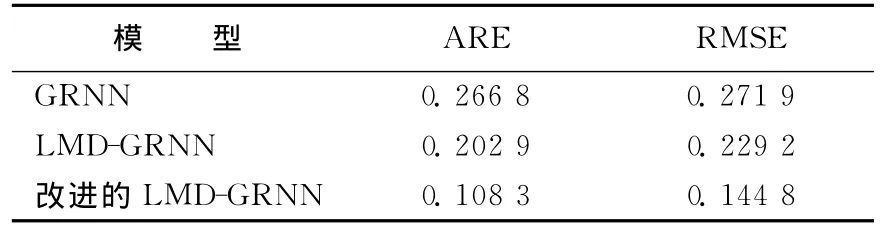
表3 几种预测模型误差
由图5、图6和表3可知,GRNN模型总体预测精度较高,但对一些风速突变点,跟踪效果较差;LMD-GRNN模型与GRNN模型相比预测精度有了较大提高,对风速突变点的跟踪效果也较好,验证了对风速进行分解预处理的必要性和LMD-GRNN模型的有效性;改进的 LMDGRNN模型的预测精度更高,跟踪风速突变点的能力更强,验证了改进的LMD-GRNN模型的有效性,也进一步验证了改进的LMD比传统的LMD分解更精确。
4 结束语
本文针对风速时间序列的非线性和非平稳性,建立LMD-GRNN组合预测模型和改进的LMD-GRNN组合预测模型。通过对某风电场风速数据的预测分析,得出以下结论:
(1)经Akima插值改进的LMD算法比传统LMD算法分解结果更精确。
(2)经LMD和改进LMD分解预处理后的模型与未分解预处理的模型相比预测精度都有较大提高,验证了对风速序列进行分解预处理的必要性。
(3)采用改进的LMD-GRNN的组合模型预测精度更高,验证了所提模型的有效性。
[1] 高 爽,冬 雷,高 阳,等.基于粗糙集理论的中长期风速预测[J].中国电机工程学报,2012,32(1):32-37.
[2] Taylor J W,Mcsharry P E,Buizza R,et al.Wind power density forecasting using ensemble predictions and time series models[J].IEEE Trans Energy Convers,2009,24(3):775-782.
[3] 吕伟才,秦永洋,孙兴平,等.Kalman滤波在地表移动观测站沉降监测中的应用研究[J].合肥工业大学学报:自然科学版,2011,34(9):1370-1374.
[4] 丁 明,张立军,吴义纯.基于时间序列分析的风电场风速预测模型[J].电力自动化设备,2005,25(8):32-34.
[5] 方江晓,周 晖,黄 梅,等.基于统计聚类分析的短期风电功率预测[J].电力系统保护与控制,2011,39(11):67-78.
[6] 张 华,曾 杰.基于支持向量机的风速预测模型研究[J].太阳能学报,2010,31(7):928-932.
[7] 孙 林.基于 WLS-SVM标准差σ预测的产品过程质量控制方法研究[J].合肥工业大学学报:自然科学版,2013,36(2):231-235.
[8] 杨秀媛,肖 洋,陈树勇.风电场风速和发电功率预测研究[J].中国电机工程学报,2005,25(11):1-5.
[9] 蔡 凯,谭伦农,李春林,等.时间序列与神经网络法相结合的短期风速预测[J].电网技术,2008,32(8):82-85.
[10] 帅海燕,龚庆武,张园园.基于广义回归网络-改进差分进化算法的污闪电压预测研究[J].电力系统保护与控制,2010,38(19):107-113.
[11] 潘 睿,刘俊勇,倪雅琦,等.基于负荷预测及广义回归神经网络的短路电流超短期预测[J].电力系统保护与控制,2010,38(18):94-99.
[12] 王晓兰,王明伟.基于小波分解和最小二乘支持向量机的短期风速预测[J].电网技术,2010,34(1):179-184.
[13] 刘兴杰,米增强,杨奇逊,等.基于经验模式分解和时间序列分析的风电场风速预测[J].太阳能学报,2010,31(8):1037-1041.
[14] 孙 斌,姚海涛.基于局域均值分解和多核最小支持向量机的 短 期 风 速 预 测 [J].太 阳 能 学 报,2013,34(9):1567-1572.
[15] 李天云,谢家安,张方彦.HHT在电力系统低频振荡模态参数提取中的应用[J].中国电机工程学报,2007,27(28):79-83.
[16] 程军圣,杨 宇,于德介.局部均值分解方法及其在齿轮故障诊断中的应用[J].振动工程学报,2009,22(1):76-84.
[17] 程军圣,张 亢,杨 宇,等.局部均值分解与经验模式分解的对比研究[J].振动与冲击,2009,28(5):13-16,201.
[18] 胡劲松,杨世锡,任达千.基于样条的振动信号局域均值分解方法[J].数据采集与处理,2009,24(1):82-86.
[19] 谢啸虎.基于固有模态分解的时频分析技术研究与应用[D].武汉:武汉理工大学,2009.
[20] 任达千,杨世锡,吴昭同,等.LMD时频分析方法的端点效应在旋转机械故障诊断中的影响[J].中国机械工程,2012,23(8):951-956.

