云环境下基于碎片影响度的提前预定资源调度策略
李 晨, 刘 博, 李 云
(扬州大学 信息工程学院,江苏 扬州 225127)
提前预定调度策略[1-2]使调度程序可以保证资源在未来一段特定时间内的有效性,增加了系统的可预测性。提前预定调度策略通常会产生大量的资源碎片,针对目前主要的资源调度模式存在的缺陷,本文提出了一种基于资源碎片影响度的提前预定资源(fragment-based advance reservations,FBAR)调度算法,利用计算几何的相关知识[3]以及一种特定结构的改进的平衡搜索树来有效管理资源碎片,同时根据各个计算节点的负载情况、长碎片阈值和本文提出的碎片影响度函数制定一种改进的提前预定资源调度策略,可有效解决因提前预定而造成的资源碎片问题,在大规模数据下提高了资源利用率和任务命中率。
1 相关知识
定义1(提前预定任务) 提前预定任务用一个三元组ti=(ri,li,di)来表示,其中,ri为最早开始时间,长度li为执行时间,截止期限di为任务的最晚完成时间(di≥ri+li)。
有2个计算节点的调度表如图1所示,在当前时间(t=0),节点1上有3个已被分配的任务,即当前正在执行并且将在t1时间结束的任务、已被预订在t3执行并在t5结束的任务A和t9~t11时间段的任务D。同样在节点2上也有3个已被分配的任务:任务B、C以及当前正在执行的任务,并且有一个新任务分配的服务请求为:准备时间ri=t6,执行长度li=t8-t6。
调度机按照一定的资源调度算法将新提交的任务分配到合理的计算节点上执行,更新调度表并将调度引用反馈给提交用户,否则拒绝执行该任务并反馈用户。
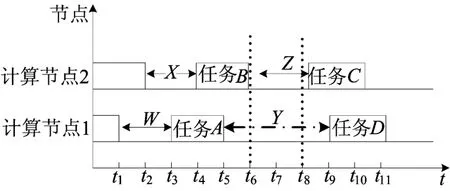
图1 简单的有2个节点的调度表
2 基于碎片影响度的提前预定策略
2.1 基于计算几何的资源调度模型
本文采用计算几何的概念[3],用平面上的1个点表示1个相应的资源碎片,图1的计算几何表示如图2所示,x轴为结束时间ET,y轴为起始时间ST,因为所有资源碎片的ET>ST,所以全部碎片的计算几何表示的点均分布在对角线的上部,由于碎片X的开始时间为t2,结束时间为t4,因此在平面上被表示为坐标X=(t2,t4)上的点。
定义2(完全包含|⊇|) 对于2个平面上的点p1=(x1,y1)、p2=(x2,y2),若x1≤x2且y1≥y2,则称点p1|⊇|p2。
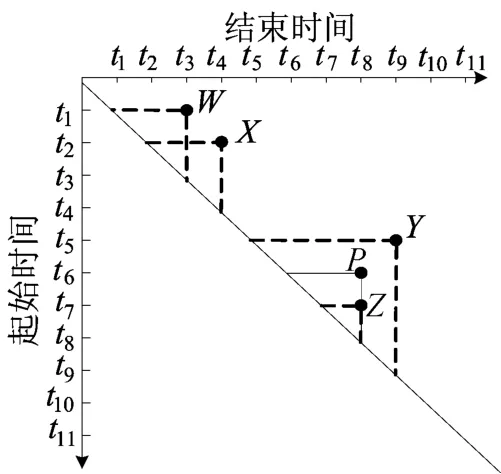
图2 图1的计算几何表示
2.2 基于碎片影响度的改进的资源调度策略
2.2.1 平面划分区域搜索策略
本文将通过计算几何的相关概念来描述带有截止期限的提前预定任务的资源调度问题[4],如图3所示。
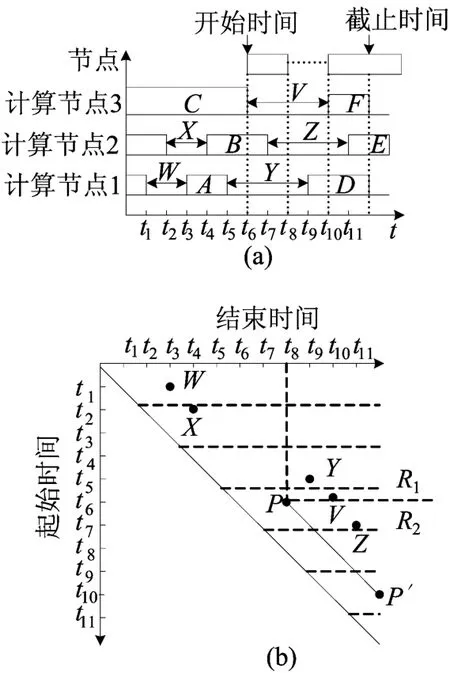
图3 带有截止期限的提前预定任务及计算几何表示
定义3(可行区域) 对于平面上的某一区域Ri以及任务tj=PP′,若有资源碎片所对应的点∀Pk∈Ri,且∃Pm∈PP′使得Pk|⊇|Pm,则称Ri为任务tj的可行区域。
为了使算法更加高效,把平面对角线的上半区域水平分割成多个子区域,每个子区域的高度为2×lmin,其中lmin代表系统估计请求任务的最小执行时间单元,如图3所示,如此分割可以使所有K个碎片点被分类成H个子集合,每一个h∈H包含了在平面上属于第h个水平切割区域的资源碎片点。
与维护一个单一的树[5]不同,在构建的H棵平衡搜索树中每个树结构对应一个水平区间,通过忽略长度小于最小执行时间单元的碎片点Pi(ETPi-STPi<lmin),致使每个资源碎片的长度不小于lmin,并且每个计算节点中2个连续的资源碎片之间的距离(两者所夹任务的执行时间)li≥lmin,因此各个计算节点上的任意2个资源碎片Pi、Pj的开始时间以及结束时间之间的距离至少为2个最小执行时间单元(STPj-STPi,ETPj-ETPi≥2lmin),所以每个水平区域所对应的平衡搜索树中的资源碎片所对应的点的数量不会超过计算节点的总数目n,并且其中属于同一计算节点的碎片数目最多为1,在选取某个资源碎片进行任务分配调度后所做的更新操作时间复杂度大大降低(n≪K)。
2.2.2 改进的平衡搜索树和资源调度策略
步骤3 将所有训练样本集XTrain(i)(i=1,2,3)分别向各自所对应标准样本集Wi(i=1,2,3)进行投影,得到每一副图像对应的系数向量,这些向量共同形成降维后的样本集HTrain(i)(i=1,2,3).
每个水平区域h={1,…,H}包含了所有开始时间STPi在[2(h-1)lmin,2hlmin)内的资源碎片点,h内的所有点用一棵改进的平衡搜索树Th来存储,调度算法通过遍历Th对水平区间h内的资源碎片按要求进行搜索。
在每棵改进的平衡搜索树Th中,资源碎片点Pi按开始时间STPi升序存储在Th的叶结点上,并由一个三元组(STPi,ETPi,RPi)来表示,其中RPi为辅助数据,包括Pi所处的计算节点编号以及该节点的负载情况和传输带宽等。
一个简单的带有截止期限的提前预定任务的资源调度计算几何模型以及h=2时的水平分割区域中资源碎片点的改进平衡搜索树结构Th=2如图4所示。
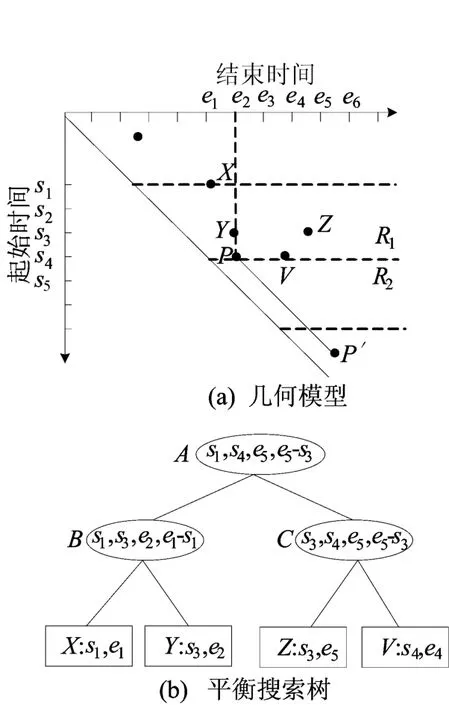
图4 计算几何模型以及平衡搜索树
图4中,s为开始时间;e为结束时间,该水平分割区域有X=(s1,e1)、Y=(s3,e2)、Z=(s3,e5)以及V=(s4,e4)4个资源碎片点。由于s1<s3<s4,则按照X→Y→Z→V的升序排列叶结点。非叶结点B存储其子树的叶子结点X、Y的开始时间STX、STY的最小值s1与最大值s3、最晚的结束时间e2以及最大碎片长度e1-s1,相应地,根A=(s1,s4,e5,e5-s3)以及非叶结点C=(s3,s4,e5,e5-s3)。
在实时调度下随着时间的推移,过期的资源碎片点将被丢弃,将平面水平分割成若干部分,并分别独立维护每个水平分割区域所对应的改进的平衡搜索树,每隔2lmin个时间单位丢弃h=1所对应的树Th=1,并对剩下的树重新标号h′=h-1,用一个循环队列记录树标号并将每棵树用哈希索引进行映射,比单树结构[6]在实时系统环境下具有更高的执行效率。
定义4(资源碎片 RF) 假设Pj=(STPj,ETPj)为提交的带有截止期限的任务ti=(ri,li,di)所对应的计算几何平面模型中PP′上的一点,若存在空闲资源点Px=(STPx,ETPx),并且有Px|⊇|Pj,则将任务ti调度在Px上执行时所产生的资源碎片 RF(ti,Px)=(STPj-STPx)∪(ETPx-ETPj),其中Pj为ti在Px上可以最早开始执行的时间所对应的点。
用户提交的任务规模大小服从正态分布N(μ,σ2),申请时间服从幂函数分布Xn(n<0),3种S型曲线函数如图5所示。
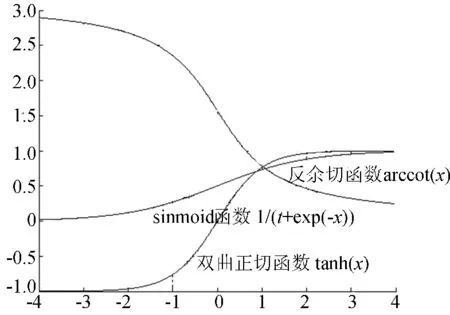
图5 3种S型曲线函数
本文通过对这3种S型曲线函数进行实验分析后选取实验结果为最平滑的sigmoid函数并对其进行改进。
定义5(碎片影响度FID) 假设存在定义4中所产生的资源碎片RF(ti,Px),则碎片影响度FID(ti,Px)定义如下:
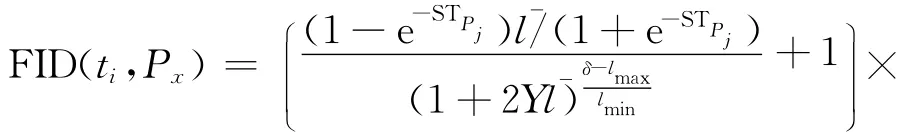
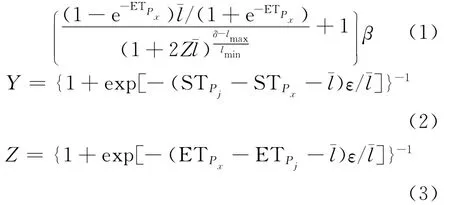
其中,β为相应的计算节点的负载程度;δ为RPx中所记录的当前计算节点中碎片长度不小于长资源碎片的碎片总长度;ε为调整参数,是由提交的任务集合的执行时间长度范围σ所决定的;lmax、lmin、分别为提交任务的最大、最小执行长度以及平均执行长度。
任务ti在点Px上的碎片影响度FID(ti,Px)越小,说明ti在Px上有着更加优先的选择性,在大规模任务集合下考虑到各个计算节点的负载均衡β可以更加有效地充分合理利用资源,增加系统的整体性能。
为了更加高效地对所有有效资源碎片进行扫描分析,将整体搜索策略分为以下步骤。
(1)扫描区域R1(除水平分割边界区域,h=1,2)。因为区域R1中所有资源碎片点的开始时间都小于任务ti的最早开始时间ri,所以在R1区域内的水平分割区域所对应的改进的平衡搜索树中所有叶结点的STPi<ri。从根结点开始按照深度优先搜索依次遍历:若某一非叶结点的子树最晚结束时间小于ri+li,则表示该非叶结点的所有叶结点代表的资源碎片均不能执行完成任务ti,深度遍历返回上一层继续执行。
(2)扫描区域R2(除水平分割边界区域,h=4)。由于区域R2内所有资源碎片点的开始时间都在任务ti的允许开始时间内,所以Th∈(R2=4)中所有叶结点的ri<STPi<di-li。从根结点开始按照深度优先搜索依次遍历:若某一非叶结点的子树的最大资源碎片长度小于li,则表示该非叶结点的所有叶结点代表的碎片的长度均不够完成任务ti,深度遍历返回上一层继续执行。
(3)扫描水平分割边界区域(P、P′所在的水平分割区域,h=3,5)。从根结点开始按照深度优先搜索依次遍历:若某一非叶结点的子树的资源碎片点的最大开始时间小于ri,则以该结点为根的子树,跳转至步骤(1),按照R1的搜索方式进行遍历,当该子树遍历完毕后返回上一层时,跳转回本步骤中的搜索方式进行遍历;若该结点的子树的资源碎片点的最小开始时间大于ri,且最大开始时间小于di-li,则以该结点为根的子树,跳转至步骤(2),按照R2的搜索方式进行遍历,当该子树遍历完毕后返回上一层时,跳转回本步骤中的搜索方式继续进行遍历;若该结点的子树的资源碎片点的最小开始时间大于di-li,则表明以该结点为根的子树的所有叶子结点所代表的碎片点均不满足任务ti的执行要求,该树遍历结束。
(4)在步骤(1)、(2)、(3)中当遍历到叶结点Px时,根据RPx中所记录的计算节点的负载参数β、传输带宽以及实际执行时间计算该叶结点所代表的资源碎片Px、调度任务ti时所造成的碎片影响度FID(ti,Px),当Px不能满足ti的截止期限要求时,该Px将不予考虑。根据以上搜索策略得到λ= (di-li)/(2lmin)个水平分割区域所对应的改进的平衡搜索树中的λ个局部最优资源碎片Ph=1,…,λ使得FID(ti,P1,…,λ)分别在Th=1,…,λ中最小,最 后 求 得 FID (ti,P1,…,λ)中 的 最 小 值FID(ti,Pk∈{1,…,λ})即为全局最优解,使得任务ti在资源碎片Pk上被调度时有着最高的全局系统性能以及任务命中率。
3 实验验证及分析
为了验证FBAR调度算法的有效性,将其与文献 [7-9]中 提 出 的 HAR(heterogeneous advance reservation)调度算法进行比较,其结果如图6所示。实验环境包括10个性能不同的虚拟机节点,各计算节点间的平均带宽为20Mb/s。
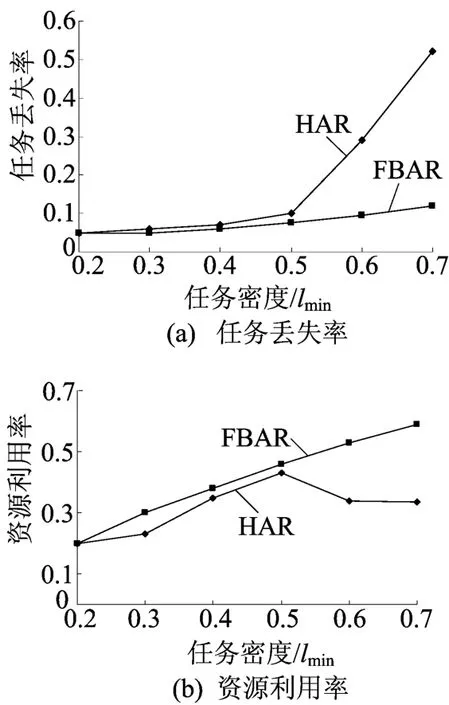
图6 不同任务密度下的任务丢失率及资源利用率
由图6可以看出,HAR调度算法的任务丢失率随任务密度增加迅速变大,显著影响着系统的利用率;FBAR调度算法的任务丢失率基本保持平稳增长,可增加系统资源的利用率。
4 结束语
本文提出了一种基于碎片影响度的提前预定任务的资源调度策略,以计算几何的形式对系统资源进行平面表示,并将平面水平分割后采用改进的平衡搜索树结构存储资源信息,结合调度所产生的资源碎片大小和碎片影响时间长短,提出碎片影响度来计算各个资源碎片的性能指标,选取最优资源碎片在满足任务需求的情况下对其进行调度,以获得比传统的调度策略更高的资源利用率和任务命中率。
[1] Min R,Maheswaran M.Scheduling advance reservations with priorities in grid computing systems[C]//Proceedings of PDCS’01,2001:172-176.
[2] 王景华,张建军,徐 娟,等.基于分布式Agent的网格任务调度模型研究[J].合肥工业大学学报:自然科学版,2010,33(2):179-181,225.
[3] de Berg M,van Krefeld M,Overmars M,et al.Computational geometry:algorithms and applications[M].2ed.New York:Springer-Verlag,2000:13-32.
[4] Castillo C,Rouskas G N,Harfoush K.Online algorithms for advance resource reservations[J].Journal of Parallel and Distributed Computing,2011,71(7):963-973.
[5] McCreight E.Priority search trees[J].SIAM Journal of Computing,1985,14(2):257-276.
[6] Xu J,Qiao C,Li J,et al.Efficient burst scheduling algorithms in optical burstswitched networks using geometric techniques[J].IEEE Journal on Selected Areas in Communications,2004,22(9):1796-1811.
[7] Figueiredo R J,Boykin P O,Juste P S,et al.Social VPNs:integrating overlay and social networks for seamless P2P networking[C]//IEEE WETICE/COPS,2008:93-98.
[8] Sotomayor B,Keahey K,Foster I.Combining batch execution and leasing using virtual machines[C]//HPDC′08 Proceedings of the 17th International Symposium on High Performance Distributed Computing,2008:87-96.
[9] Matsunaga A,Tsugawa M,Fortes J.CloudBLAST:combining mapreduce and virtualization on distributed resources for bioinformatics applications[C]//IEEE Fourth International Conference,2008:222-229.

