分布式电源对配电网电流保护影响的语义规则库分析方法
马晓博,柯德平,孙元章,程波
(1.武汉大学电气工程学院, 430072, 武汉; 2.湖北省电力公司发展策划部, 430077, 武汉)
分布式电源对配电网电流保护影响的语义规则库分析方法
马晓博1,柯德平1,孙元章1,程波2
(1.武汉大学电气工程学院, 430072, 武汉; 2.湖北省电力公司发展策划部, 430077, 武汉)
为解决分布式电源(DG)接入传统配电网导致三段式电流保护无法正常工作的问题,提出了一种能判断一般的配网系统中DG接入对电流保护影响的语义规则库分析方法。首先,使用语义规则来设置DG对电流保护影响的校核,每条规则依次刻画了不同短路场景下对应电流保护的Ⅰ段、Ⅱ段和Ⅲ段正确动作的判定条件:若所有规则按顺序校验通过,则判断DG接入方案不会对三段式电流保护产生影响;反之,保护则可能拒动或误动。然后,提出一种应用该规则库的DG准入容量优化方法,通过规则库生成DG准入容量的约束条件,在保证三段式电流保护可靠动作的前提下,优化多个DG的接入容量使其容量之和最大。仿真结果表明:当DG接入容量在8.19 MV·A以内时,三段式电流保护均可以正确动作,所提方法不仅能准确求解配电网中DG的准入容量,而且操作简单、易于工程实现。
分布式电源;配电网;三段式电流保护;准入容量;语义规则库
分布式电源(DG)大规模接入中低压配电网改变了传统配电网的单电源辐射式供电模式,将直接威胁电网的安全稳定运行。目前,已有大量文献研究DG接入对配电网的线路潮流[1]、静态电压[2-3]、谐波[4]、网损[5]和短路电流分布[6-7]的影响,其中,评估DG接入对配电网中传统三段式电流保护的影响引起了众多学者的广泛关注。从理论上讲,对于给定的配网拓扑结构和参数、相应的阶段式电流保护配置和整定值,正确判断DG接入后对保护的影响可以按照一般性遍历法,例如,文献[7]中穷举所有可能出现的短路电流(分别对应不同短路位置、类型或程度),并检验各个短路电流下系统所有保护的Ⅰ、Ⅱ和Ⅲ段的选择性和灵敏性。很显然,遵循此一般性遍历法的判断过程将计算量巨大,不具有实际可操作性。文献[8-9]在文献[7]的基础上,只对有限短路场景(包括短路位置、类型和程度)下系统部分保护的相应段进行校验,在保证判断结果准确性的前提下大大节省了计算时间。但是,此类研究均只针对各自所研究的配网系统以及DG接入情况(包括接入数量、类型、位置和容量),其得到的校验过程明显不具有一般性,即无法移植于其他配网系统和/或DG接入情况。从工程应用的角度看,更希望基于一种一般性的语义规则库来指导校验过程。
针对上述问题,本文通过理论推导、泛化得到一般的配网系统中分析DG接入对传统三段式电流保护影响的实用化语义规则库。当规则库中的所有规则逐条校验通过时,可以判断DG接入方案将不会影响保护的正确动作;反之,保护则可能拒动或误动。该规则库在保证判断结果的准确性的前提下,排除了所有非必要的校验步骤,因而具有较高的校验效率。将该规则库应用于目前广受关注的DG准入容量优化的研究问题中,即通过规则库便捷地生成准入容量计算的约束条件,进一步使用差分进化(DE)算法搜索多个DG的最优接入容量,在保证三段式电流保护正确动作的前提下使其接入容量之和最大。
1 DG的短路计算模型
在短路计算中,通常认为当电源容量大于3倍短路容量时,可以看做无限大容量的电源,其短路的暂态过程可以忽略[10]。接入低压配电网的DG容量一般有限,故障电流衰减较慢[7],鉴于此,本文研究DG提供的短路电流时考虑其暂态过程,通过分析不同类型DG的短路暂态运行特性,归类出统一的短路计算模型。
接入配电网的DG按照其接口可以分为基于同步发电机的DG、基于异步发电机的DG以及基于逆变器的DG 3大类。基于同步发电机的DG一般根据戴维南定理等效为一个电源串联电抗的模型。以风力发电机为代表的异步发电机在短路故障时,按照磁链守恒原则,其定子和转子绕组中都会产生相应的电流分量以保证定子和转子绕组中的交变磁链不发生突变,因此,异步发电机可以用一个与转子绕组的磁链成正比的电动势,即次暂态电动势以及相应的次暂态电抗作为短路暂态过程的电源和电抗[10]。以光伏发电为代表的逆变型DG可以通过改变拓扑结构和调整控制策略将故障电流限制为额定电流的1.5倍以内[11],其对配电网三段式电流保护的影响一般很小,在本文研究中不作考虑。
综上分析可知,不同类型DG在短路故障分析中均可近似等效为电势源串联电抗的模型。
2 DG接入对配电网电流保护的影响分析
本文的研究对象是具有辐射式网架结构的配电网,通过详细分析DG上游、下游以及相邻线路上发生短路故障时DG接入对配电网三段式电流保护的影响,泛化得到分析一般系统中DG接入对保护影响的语义性步骤,即语义规则库。语义规则库中包含若干条顺序执行的语义规则,这些一般性的语义规则适用于任意的配网系统和DG接入情况,且每条规则通过描述性语言指导操作者该如何构造短路场景,并选择哪些保护的Ⅰ、Ⅱ或者Ⅲ段进行校验。这样,操作者无须根据所研究的系统来分析确定校核步骤,只要顺序执行规则库中的语义规则便能高效准确地判断DG接入方案对保护的影响,同时可以避免由于操作者分析水平受限而导致的不准确校验结论。
2.1 故障发生在DG下游
图1是某典型10 kV配电网示意图,由2条馈线组成,首先从单DG接入母线b7开始,进而推广到多DG的一般化情况。
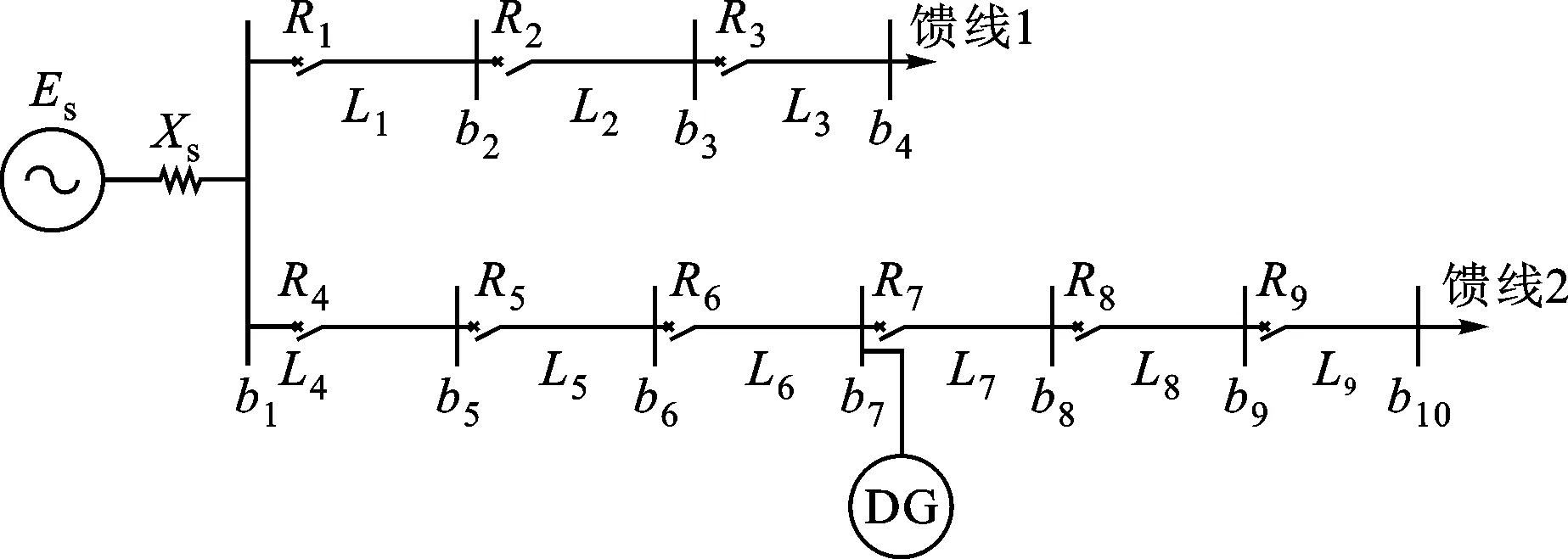
b1~b10分别表示各段母线;L1~L9表示各条子线路;R1~R9分别表示与各条子线路相对应的电流保护装置;Es、Xs分别为系统电源的内电势和电抗图1 DG接入的配电网系统示意图
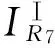
DG对下游故障点短路电流的助增作用导致下游各保护的保护范围都相应增大,假设R7和R8所在线路的末端母线上分别发生三相短路故障,则流过R7和R8的短路电流以及其Ⅰ段整定值分别为
(1)
(2)
(3)
(4)
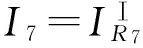
(5)
将Zsd代入式(3),可得
(6)
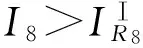
(7)
式中E″d和X″d分别为分布式电源的次暂态电动势和次暂态电抗,Z为系统电源到DG安装处之间的阻抗,所以
(8)
一般情况下,发电机的次暂态电势取1.05~1.15[12],即式(8)的约束条件不满足,这意味着在R7的Ⅰ段保护不误动的前提下,R8的Ⅰ段也不会误动作。因此,可以得到如下结论:若DG的下游有2条及以上线路,只需保证距离DG最近的保护Ⅰ段的保护范围不延伸到下一段线路,下游其他保护的Ⅰ段均可以正确动作。
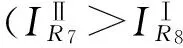
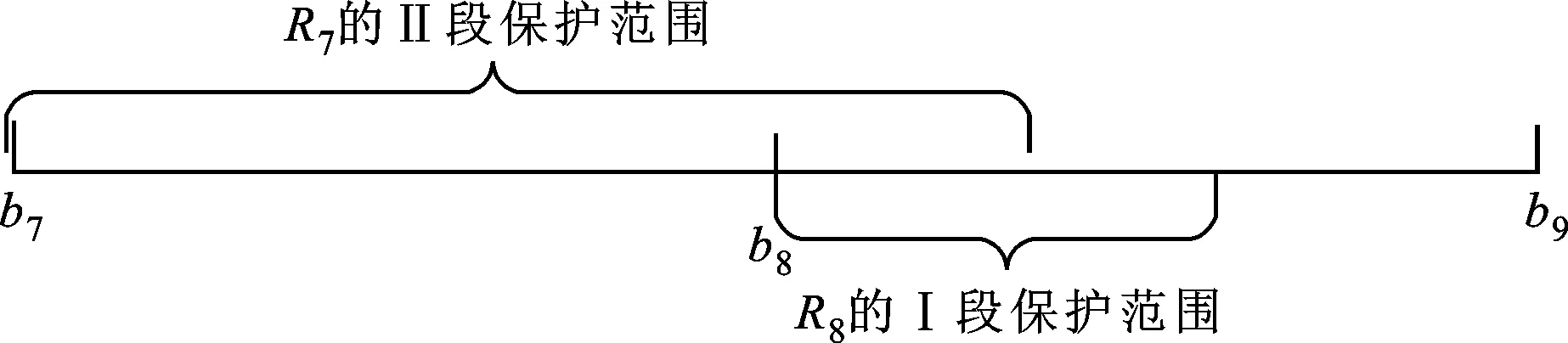
图2 电流保护装置R7与R8的配合示意图
多个DG同时接入配电网对保护Ⅰ段的影响如图3所示,其分析过程与单个DG相似:只要保证距离最下游DG最近的保护Ⅰ段的保护范围不超过其所在线路的全长(如图3系统中R4不误动,其Ⅰ段整定值大于b5上发生三相短路时流过R4的短路电流),则该DG下游所有的保护均能正确动作;只要保证距离下游倒数第2个DG最近的保护Ⅰ段的保护范围不超过其所在线路全长(如图3中R3不误动),则当该DG下游发生短路故障时,故障点到DG之间的所有保护均能正确动作;上述过程持续进行直到最首端DG。
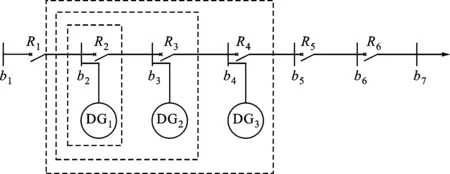
图3 多DG组成的电源系统对其下游保护的影响
2.2 故障发生在DG上游
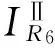
当多个DG接入时,分析过程与上节类似:首先保证距离最上游DG最近的保护Ⅱ段不误动,在该DG上游任意位置发生短路时,其上游所有保护均能正确动作;然后,保证距离上游第2个DG最近的保护Ⅱ段不误动,上游任意故障点到该DG之间的所有保护均能正确动作(不误动作)。上述过程持续进行直到最末端的DG,其示意图如图4所示。
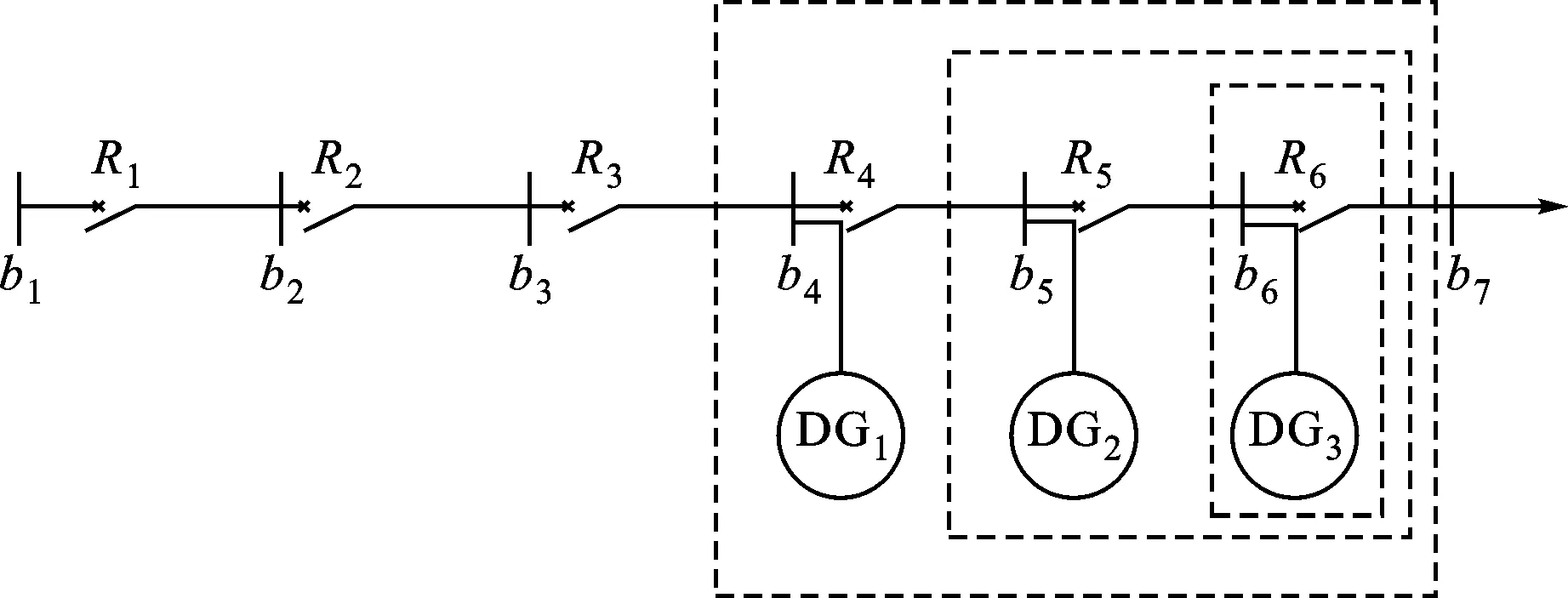
图4 多DG组成的电源系统对其上游保护的影响
上述分析中只考虑了保护的Ⅰ和Ⅱ段,关于过电流保护(Ⅲ段)的讨论如下:①对于DG下游的保护,DG接入使流过Ⅲ段保护的短路电流增大,灵敏度提高;②对于DG上游的保护,当上游发生故障时,保护可能因流过DG提供的反向短路电流而误动作,但因DG都配备了防孤岛装置,将在一定时限后切除处于孤岛运行的DG,由于该时限通常远小于过电流保护的时延,故能避免造成保护Ⅲ段误动作;③对于DG上游的保护,当下游发生故障时,保护可能因流过的短路电流减小而出现拒动现象(当Ⅲ段保护作为相邻线路的远后备保护时,要求至少保护到下一段相邻线路的全长)。DG接入对配电网过电流保护的影响如图5所示。取临界情况分析,在图5中,当R2的Ⅲ段保护范围恰好缩小至下一段相邻线路末端,即母线b4短路时,流过R2的短路电流恰好等于其Ⅲ段保护的启动值,计算得到的DG1容量为其临界容量,即DG的实际接入容量小于此临界容量时可以保证R2的Ⅲ段作为远后备保护不拒动。需要说明的是:由于Ⅲ段的动作电流一般较小,所以按照上述方法计算得到的临界容量通常都远远大于DG的实际接入容量。
对于多个DG接入的情况,最上游DG(如DG1)的临界容量的确定不受下游DG的影响,此规律可依次类推。但是,此容量却会影响下一个相邻DG的临界容量,其容量越大,下一个DG的临界容量也愈大。因此,取极端情况,即上游所有DG容量均为临界容量时,计算相邻下一个DG的临界容量,如DG1为临界容量时,计算DG2的临界容量。综上所述,为保证Ⅲ段保护不误动,要使DG实际接入容量小于计算得到的临界容量。
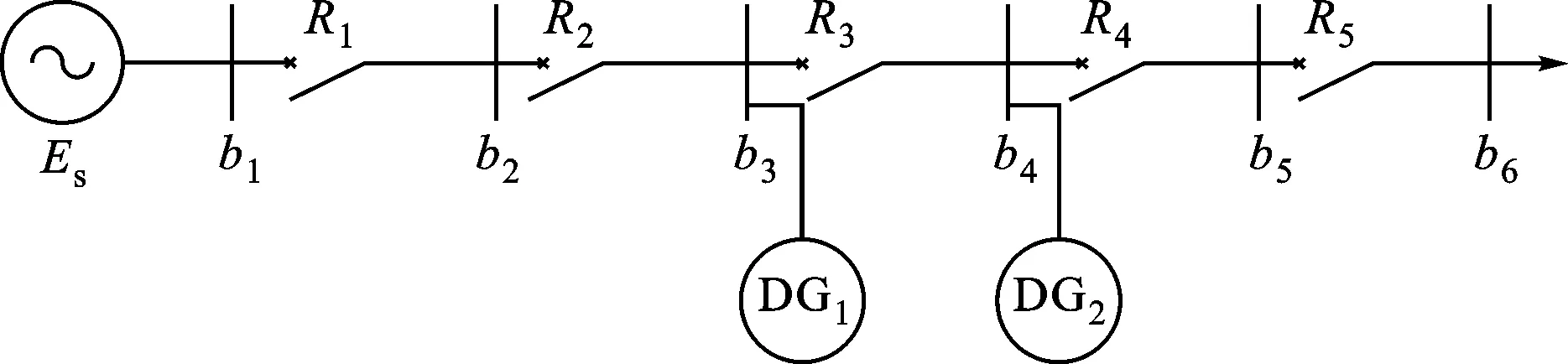
图5 DG接入对配电网过电流保护的影响
2.3 故障发生在DG相邻馈线
图1中,DG的相邻线路发生短路故障时,相邻线路上的保护可能因DG提供的反向故障电流而误动作。例如L2上发生短路故障可能导致R1的Ⅰ段保护误动,而实际情况分析如下:DG和系统电源组成的等效电源Esd和等效电抗Zsd分别为
(9)
(10)
由于Xs≤X″d+Z4+Z5+Z6,可得Esd≈Es,Zsd≈Xs,表明流过相邻线路上保护的短路电流基本不受DG的影响。对于多个DG接入的情况,上述结论依然成立,因为DG内电势相对于相邻线路上短路点的转移阻抗要远远大于系统电源内电势到短路点的转移阻抗,因此前者所提供的短路电流相对于后者而言可以忽略不计。
2.4 语义规则库的推导
总结上述DG接入辐射式配电网对保护Ⅰ、Ⅱ和Ⅲ段的影响,泛化得到系统性校验步骤并整理成如下语义规则。
(1)由上文分析可知,DG由于其容量限制一般不会对其相邻馈线上的保护产生影响,因此,以配电网系统的每条馈线为研究对象进行分析,若一条馈线上接有n个DG,由系统电源端向馈线下游依次排布,分别记为DG1,DG2,…,DGn。
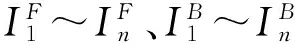
(3)若上述判定条件不能全部满足,则表明DG接入会对电流保护产生影响,此DG接入方案将导致保护误(或拒)动作。
(4)在表1的Ⅲ段校验中,给定“短路场景”和“对应保护”是为了计算DG1,DG2,…,DGn的临界容量,记为S1max,S2max,…,Snmax,若DG的实际接入容量均小于其临界容量,即判定条件S1max>SDG1,S2max>SDG2,…,Snmax>SDGn均满足,则DG接入不会对保护的Ⅲ段产生影响。
(5)实际经验[7]表明,关于Ⅰ段的判定条件最容易不满足,而关于Ⅲ段的判定条件则较易满足。因此,从节省计算时间的角度看,一旦有判定条件不满足即无须进行后续校验,应安排先校核Ⅰ段,其次是Ⅱ段,最后是Ⅲ段。
3 语义规则库的应用
根据上节中推导得到的语义规则库可以分析一
般的配网结构和参数以及DG接入情况下保护是否能正确动作。本文将进一步扩展其应用,优化多个DG接入配电网的准入容量,相应的数学模型如下
max (SDG1+SDG2+…+SDGn)
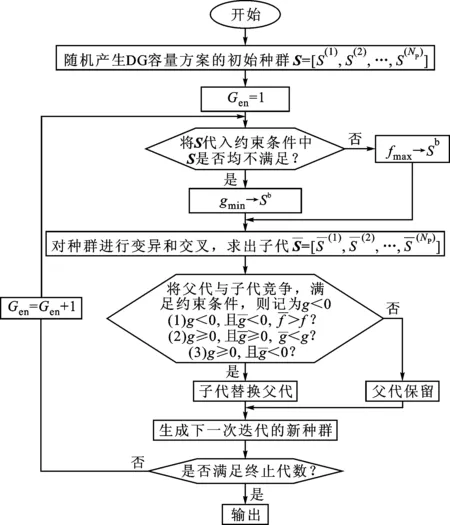
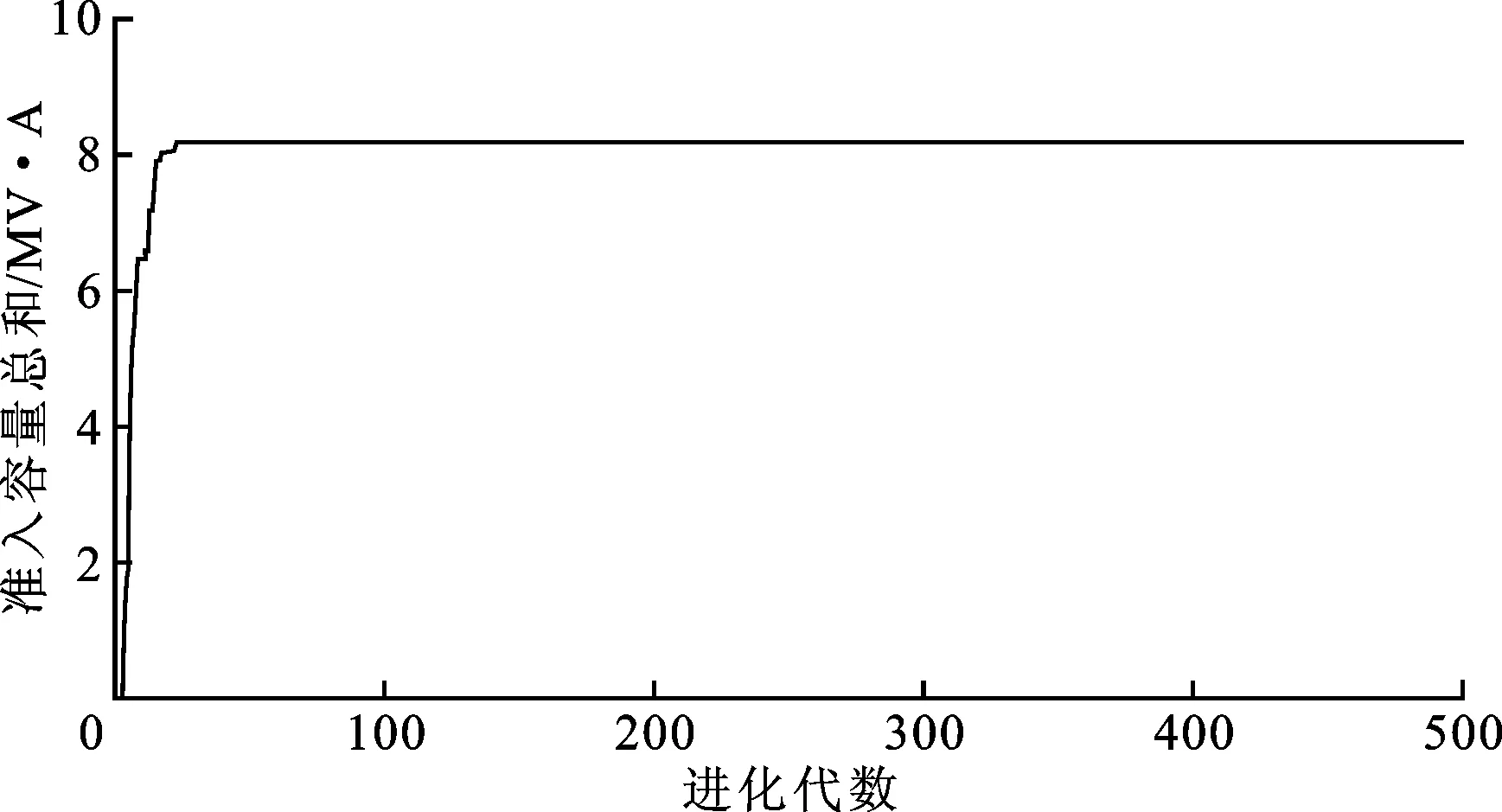
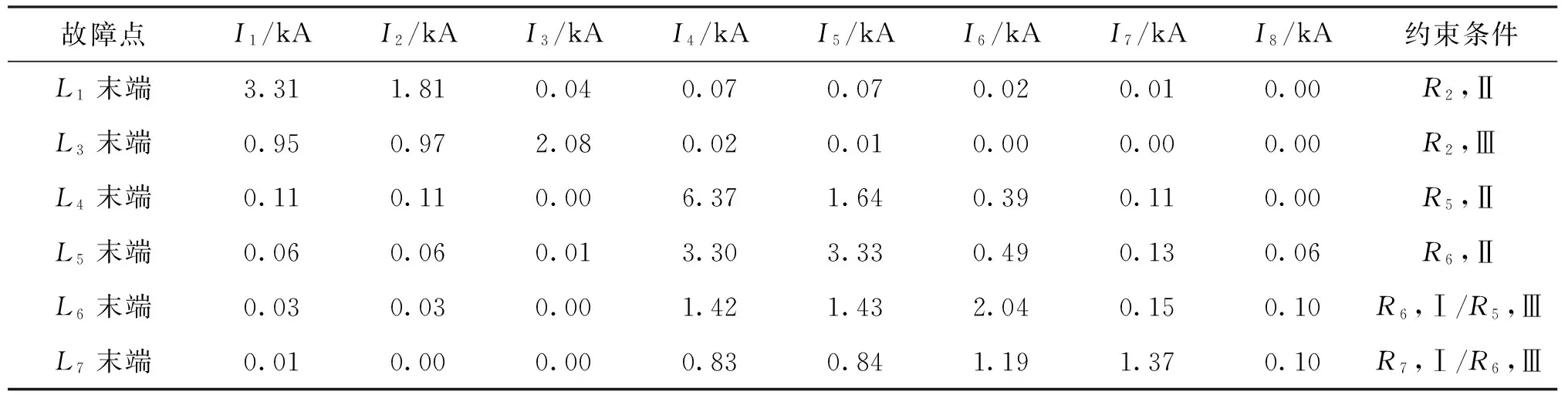
s.t.gi(SDG) (11) 式中:SDG1,SDG2,…,SDGn分别为DG1,DG2,…,DGn的准入容量;gi(SDG) 相较于现有文献对DG准入容量的计算方法,约束优化问题式(11)则更具有一般性,即针对一般性配电网络以及DG接入情况计算其准入容量。由于语义规则库的易解读性,当求解具体的算例时,可以快速地形成具体的目标函数和优化条件。例如,在图1系统b3、b6、b7处同时接入DG,目标函数取max(SDG1+SDG2+SDG3),且根据前述语义规则库可以快速准确地形成保证保护正确动作的约束条件,具体优化模型如下 (12) 本文采用差分进化算法(DE)对配电网中DG准 入容量进行优化配置,Gen表示进化代数,NP为种群规模,Sb表示种群中的最优个体,f为关于准入容量的目标函数,g为约束条件。DG准入容量的差分进化算法流程如图6所示。 图6 DG准入容量的差分进化算法流程图 用于仿真计算的配电网系统如图1所示,架空线路(LGJ-120/25)的参数为R=0.27Ω/km,X=0.347Ω/km;电缆线路(YJLV22-150)的参数为R=0.259Ω/km,X=0.093Ω/km。L1~L9的长度分别为4、6、6、2、2、7、7、14、14km,每条母线处各接有额定容量为2MV·A、额定功率因数为0.85的负荷。在L1~L2、L4~L8配置三段式电流保护装置,L3和L9位于馈线末端,配置两段式电流保护(Ⅰ段和Ⅲ段),本文选取DG的次暂态电抗的标幺值(电抗的有名值与基准值的比值)为0.1 ,以DG 容量为基准容量。 运用DE算法求解多个DG接入配电网的准入容量优化模型(12),其参数设定为:种群规模NP=50,交叉因子CR=0.9,变异因子F=0.9,进化代数Gen=500,计算一次所需时间t=18.86s,由于DE算法的优化结果具有不确定性,为了得到更加准确的DG准入容量,将DE算法连续运行50次,选取使目标函数值最大的优化结果作为DG的准入容量。图7给出了DE算法得到最优解的搜索过程, 图7 多个DG准入容量的搜索过程 从图7可以看出,当DE算法终止搜索时DG接入容量总和最大值为8.19MV·A,对应于3个DG的接入容量分别为S1=4.55MV·A,S2=2.89MV·A,S3=0.75MV·A,因此,在满足继电保护可靠动作的前提下,配电网允许接入的DG最大容量如表2所示。 表2 多个DG接入配电网的准入容量 将3个DG分别以4.55、2.89和0.75MV·A接入配电网母线b3、b6、b7处,计算不同短路场景下流过对应保护的短路电流,计算结果见表3。表3结果表明,通过优化模型得到的DG准入容量可以保证配电网原有三段式电流保护可靠动作,从而验证了所提语义规则库分析方法的有效性。 表3 多个DG接入不同短路场景下流过对应保护的短路电流 本文通过理论推导并考虑工程实际,提出一种实用化语义规则库用于指导分析DG接入后对配电网传统三段式电流保护的影响。该规则库通过描述性语言来设置对保护装置影响的校核规则,因此具有一般性,能针对任何辐射式配网系统及DG接入情况,快速准确地判断其对三段式电流保护的影响。以此语义规则库为基础,进一步建立了DG准入容量优化模型,能方便地求解一般性配网系统及DG接入情况下的准入容量。算例仿真验证了所提语义规则库分析方法的正确性。 [1] 胡骅, 吴汕, 夏翔, 等. 考虑电压调整约束的多个分布式电源准入功率计算 [J]. 中国电机工程学报, 2006, 26(19): 13-17. HU Ye, WU Can, XIA Xiang, et al. Computing the maximum penetration level of multiple distributed generators in distribution network taking into account voltage regulation constraints [J]. Proceedings of the CSEE, 2006, 26(19): 13-17. [2] SU C L. Stochastic evaluation of voltages in distribution networks with distributed generation using detailed distribution operation models [J]. IEEE Transactions on Power Systems, 2010, 25(2): 786-795. [3] SENJYU T, MIYAZATO Y, YONA A, et al. Optimal distribution voltage control and coordination with distributed generation [J]. IEEE Transactions on Power Delivery, 2008, 23(2): 1236-1242. [4] 江南, 龚建荣, 甘德强. 考虑谐波影响的分布式电源准入功率计算 [J]. 电力系统自动化, 2007, 31(3): 19-23. JIANG Nan, GONG Jianrong, GAN Deqiang. Computing the maximum penetrating level of distributed generators in distribution network by taking into account of harmonic constraints [J]. Automation of Electric Power System, 2007, 31(3): 19-23. [5] 范雪峰, 夏懿, 贾春蓉, 等. 融合网损约束的分布式电源容量优化布置分析 [J]. 电力系统及其自动化学报, 2013, 25(5): 121-126. FAN Xuefeng, XIA Yi, JIA Chunrong, et al. Analysis of optimal placement of distributed generation capacity with limited power grid lose [J]. Proceedings of the CSU-EPSA, 2013, 25(5): 121-126. [6] NIMPITIWAN N, HEYDT G T, AYYANAR R, et al. Fault current contribution from synchronous machine and inverter based distributed generators [J]. IEEE Transactions on Power Delivery, 2007, 22(1): 634-641. [7] 王江海, 邰能灵, 宋凯, 等. 考虑继电保护动作的分布式电源在配电网中的准入容量研究 [J]. 中国电机工程学报, 2010, 30(22): 37-43. WANG Jianghai, TAI Nengling, SONG Kai, et al. Penetration level permission of DG in distributed network considering relay protection [J]. Proceedings of the CSEE, 2010, 30(22): 37-43. [8] 陶顺, 郭静, 肖湘宁. 基于电流保护原理的DG准入容量与并网位置分析 [J]. 电网技术, 2012, 36(1): 265-270. TAO Shun, GUO Jing, XIAO Xiangning. Analysis on allowed penetration level of distributed generation and its grid-connected position based on principles of current protection [J]. Power System Technology, 2012, 36(1): 265-270. [9] 冯希科, 邰能灵, 宋凯, 等. DG容量对配电网电流保护的影响及对策研究 [J]. 电力系统保护与控制, 2010, 38(22): 156-165. FENG Xike, TAI Nengling, SONG Kai, et al. Research on the impact of DG capacity on the distribution network current protection and countermeasure [J]. Power System Protection and Control, 2010, 38(22): 156-165. [10]王成山, 孙晓倩. 含分布式电源配电网短路计算的改进方法 [J]. 电力系统自动化, 2012, 36(23): 54-58. WANG Chengshan, SUN Xiaoqian. An improved short circuit calculation method for distribution network with distributed generations [J]. Automation of Electric Power System, 2012, 36(23): 54-58. [11]秦岭, 谢少军, 杨晨, 等. 太阳能电池的动态模型和动特性 [J]. 中国电机工程学报, 2013, 33(7): 19-26. QIN Ling, XIE Shaojun, YANG Chen, et al. Dynamic model and dynamic characteristics of solar cells [J]. Proceedings of the CSEE, 2013, 33(7): 19-26. [12]陈慈萱. 电气工程基础 [M]. 北京: 中国电力出版社, 2012. (编辑 刘杨) Analysis of Semantic Rules for the Influences of Integrating Distributed Generations on the Distribution Network Current Protections MA Xiaobo1,KE Deping1,SUN Yuanzhang1,CHENG Bo2 (1. School of Electrical Engineering, Wuhan University, Wuhan 430072, China;2. Hubei Electric Power Company, Wuhan 430077, China) An applicable analysis of semantic rules that consider the influences of integrating distributed generations (DGs) on the distribution network current protections is proposed to effectively solve the malfunction of existing three-phase current protections. The semantic rules are used to describe the decision condition of three-phase current protections correct operation under different short circuit scenes. It is judged that the integrating DGs have no influence on the current protections in a generic distribution network if the semantic rules pass the validation process in order, otherwise it will lead to either malfunction or movement resistance. Then, the base of rules is applied to generate constraints for calculating the permitted capacities of DGs for integration. Specifically, the capacities of the integrated DGs are optimized so that the total capacity of them is maximized while the existing over-current protections can normally operate. Simulation results show that the DG capacity within 8.19 MV·A can ensure the current protection correct operation, and the high accuracy and efficiency of the presented rules are verified. distributed generation; distribution network; three-phase current protection; permitted capacity; semantic rules 2015-04-16。 马晓博(1990—),女,硕士生;柯德平(通信作者),男,博士,讲师。 国家重点基础研究发展计划资助项目(2012CB215101)。 时间:2015-09-11 10.7652/xjtuxb201510018 TM71 A 0253-987X(2015)10-0109-07 网络出版地址:http://www.cnki.net/kcms/detail/61.1069.T.20150911.1047.002.html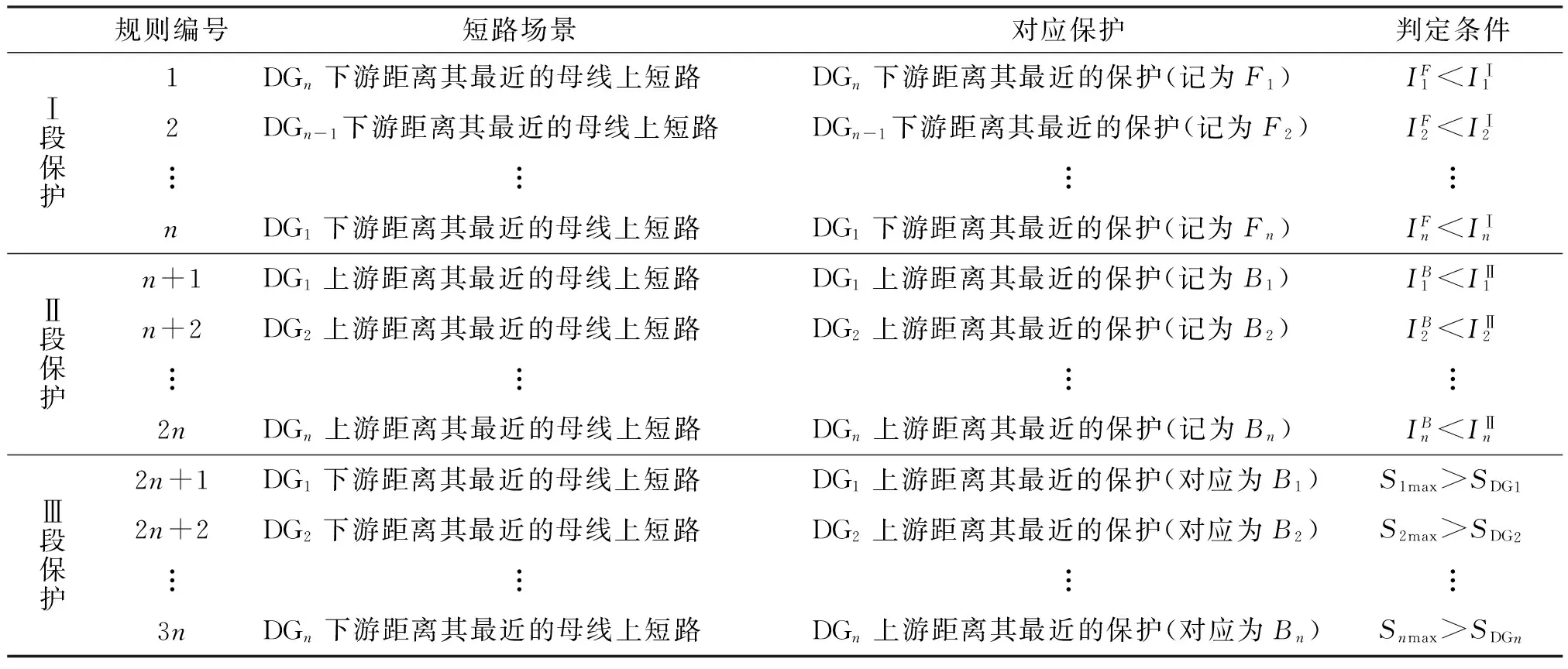
4 算例分析

5 结 论

