最短特征线段多分类器系统设计

丁建坤,韩德强,杨艺



最短特征线段多分类器系统设计

丁建坤1,韩德强1,杨艺2

模式识别理论与方法的研究近年来取得了诸多进展[1],然而在复杂环境下,单一分类器效果往往不甚理想。多分类器系统是应对复杂环境下模式识别问题的重要手段,引发了广泛的关注。目前,多分类器融合技术已广泛应用于图像识别、故障诊断、生物认证,医疗诊断等诸多领域[2-5]。

学者们从多分类器系统的不同层面开展了研究。在多个成员分类器生成方面,设计实现了基于不同训练样本[6]、基于不同特征子空间以及选取不同的分类算法[7]等多种形式的方法。1992年,Kira等提出了Relief算法[8],从特征评价的角度分析了成员分类器的性能及选择。在此基础上,Marko等提出了ReliefF、RReliefF等改进算法[9]。在多分类器融合有效性方面,Dietterich最早指出,并非多个分类器的融合一定能够获取更优的分类性能,不同成员分类器间的差异性是关键所在[10]。梁绍一等对现有的差异性度量方法进行了总结,并提出了基于几何关系的差异性度量方法[11]。多分类器融合规则方面,Xu等在1992年针对成员分类器的输出形式进行了分析研究[12],并总结了一系列的分类器融合方法,如投票法、Bayes法以及DS证据理论方法等。

成员分类器(个体分类器)的设计问题是多分类器系统设计的前提,其输出形式也决定了后续融合规则的选取[12]。邻域型分类器是一个很重要的分支,最近邻(NN)分类器[13]是一种最具代表性的简单而有效的邻域型分类算法,但是在训练样本数较小的情况下性能会受限。基于特征线(通过来自同一类的两个训练样本点的直线)的分类器,如最近特征线(NFL)[14]是NN的一种改进算法,以测试样本点到特征线的距离为决策依据,但在扩充了训练样本空间的同时,特征线的内、外穿越情况给NFL带来了错分类问题[15]。针对NFL存在的穿越缺陷,出现了许多特征线的改进方法,如最短特征线段(SFLS)[15]、核最近特征线(KNFL)[16]等方法。

本文选用SFLS作为成员分类器分类算法。SFLS作为NFL的改进算法,用特征线段代替特征线作为决策依据,可避免内、外穿越问题,且具备诸多优良的分类特性[15]。将SFLS用于多分类器系统,有望进一步提升分类性能,然而SFLS仅输出类别标签,仅利用成员分类器输出的类别标签进行表决(投票)融合,会造成信息损失。本文利用SFLS工作机理,以模糊隶属度对输出建模更多地保留输出细节以减少信息损失,进而利用基于模糊的证据融合规则实现成员分类器的度量级融合,提升了分类精度。实验结果验证了所提方法的合理性和有效性。

1 多分类器系统概述

多分类器系统因其能有效提高分类性能,在模式识别领域受到越来越多的关注并得到了广泛应用。多分类器系统的原理框图如图1所示。

图1 多分类器系统框图

图1中ei(i=1,2,…,M)代表各成员分类器。通过选择合适的融合规则,在融合决策中心利用各成员分类器的输出结果进行融合分类。成员分类器输出结果主要有3种形式[12]:摘要级(也称抽象级),即输出仅为类别标签;排序级,即输出属于各类别可能性大小的顺序;度量级,即输出一系列度量值,代表样本点属于各类别的可能性。

对不同的成员分类器输出形式采用不同的融合方式,对于上述3种输出形式,均可采用投票融合。对排序级输出可采用排序融合方式[17],对于度量级的输出形式可以利用DS证据推理[12]、模糊推理[5,7]等方法进行融合。在多分类器系统中,成员分类器的分类性能、输出形式以及成员分类器之间的差异性都会影响到多分类器系统的性能[10-12]。本文的工作主要关注成员分类器设计、融合规则选取及对多分类器系统性能的影响。

2 基于最短特征线段的多分类器系统

2.1 最短特征线段分类器

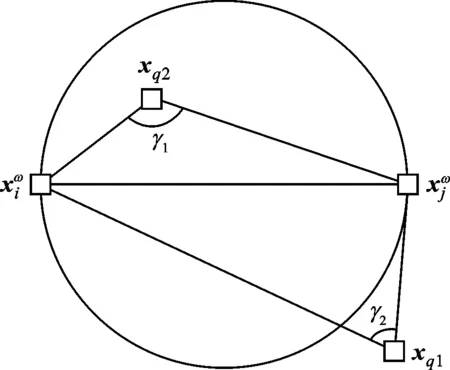
图2 特征线段和测试样本点相对位置关系

(1)

(2)在被标记的特征线段中,寻找长度最短的特征线段,则此特征线段所属的类别即为该待测样本点被判定的类别,如果没有特征线段被标记则拒绝识别该待测样本点。

SFLS保留了NFL的优点,利用样本点的两两组合代替原始样本点作为判断的依据,充分地利用了样本信息。SFLS使用的是特征线段,确定了待分类样本点与通过该特征线段的特征直线的距离上界,这样即保持了NFL优良的分类特性,又避免了NFL的内、外穿越问题[15]。SFLS中由特征线段构成的特征空间具有一个对分类器来说很好的性质,即聚合性。但是,SFLS的输出仅为类别标签,丢掉了许多有用信息,不利于进一步的多分类器融合,本文在对SFLS内部工作机理分析研究的基础上,对其输出形式重新建模,以隶属度形式输出,便于多分类器系统做更精细的度量级融合。

2.2 SFLS分类器输出度量化

特征线段长度越短,则待测样本属于该类别的可能性越大,即特征线段长度d的单调递减函数可以作为隶属度生成函数,负指数函数、反比例函数等函数形式比较简单,被广泛使用。当d的取值接近于0时,反比例函数取值会非常大,趋于无穷,并且在d=0时反比例函数无法计算和使用(分母不能为0),而负指数函数有映射关系:当d=0时,exp(-d)=1;当d→+∞时,exp(-d)→0+。相对而言,负指数函数形式更适于生成隶属度,且鲁棒性更强,因此本文选择负指数函数作为隶属度生成函数,即待测样本点xq对ωi类的隶属度为

(2)

2.3 模糊-证据融合方法

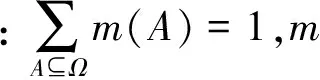
对于辨识框架Ω中的某个命题A,计算信任函数Bel(A)和似真函数Pl(A)

(3)

(4)

区间[Bel(A),Pl(A)]可用于表示A的不确定性程度。∀A⊆Ω,A≠∅,Ω上的两个mass函数m1、m2的Dempster组合规则为

(5)

2.3.2 由隶属度至mass函数的生成方法 应用证据理论进行融合决策,首先要生成mass函数。本文中SFLS的量化输出形式是隶属度,因此这里关注由隶属度至mass函数的生成方法。

设辨识框架Ω={ω1,ω2,…,ωn},θj(ωi)表示第j个成员分类器中,待测样本xq对ωi类的隶属度,则根据隶属度生成mass函数有谨慎有序加权平均证据推理(COWA-ER)方法[19]、α-cut方法[20]、直接设定焦元组方法。

(1)平均证据法。首先,分别以悲观的方式和乐观的方式选出待测样本对各类别的隶属度,即选出样本对各类别的最小隶属度和最大隶属度,得到矩阵

(6)

其次,将矩阵E中的每个元素对E的最大值归一化得到

(7)

最后,根据E′生成mass函数。E′中以悲观方式得到的ai用以表征样本属于类别ωi的信任度,即Bel(ωi)=ai;乐观方式得到的bi用以表征样本属于类别ωi的似真度,即Pl(ωi)=bi;样本属于类别ωi的不确定程度用区间[Bel(ωi),Pl(ωi)]的长度表示,即bi-ai。由此可以生成mass函数,即

(8)

(2)α-cut方法。对隶属度重新排序,得到一组顺序{π1,π2,…,πn},满足

设Bk(k=1,…,n)为转换后的mass函数焦元,则有

(9)

(3)直接设定焦元组方法。首先对隶属度进行归一化,即

(10)

将隶属度归一化后,可按如下两种方式生成mass函数:方式1[21]是仅对单点焦元和全集赋值,β为折扣系数,即

(11)

该方法预设了焦元结构为单点焦元以及辨识框架的全集,将概率值打折扣赋予单点焦元,剩余部分赋给全集以表征“未知”,当β=1时简化为概率形式;方式2[21]是仅对单点焦元、其补集和全集赋值,即

(12)

该方法将mass值赋予单点焦元及其相应补命题的焦元,剩余部分赋予全集。根据以上方法生成mass函数之后,就可以根据Dempster规则进行融合,得到融合后的mass函数。

2.3.3 由证据至概率的转换及决策 基于多个证据函数组合之后所获取的新mass函数实现决策时,往往需要借助由证据至概率的转换方法。这里使用经典的Pignistic概率转换[22],定义为

(13)

式中:|B|为集合B中元素个数。利用式(13)将融合后的mass函数转换为Pignistic概率BetP(ωi) (i=1…n),由此做出最终融合决策,即

Pdec=BetP(ωk)=maxi(BetP(ωi))

3 实验比较和分析

为了验证最短特征线段多分类器系统的有效性,本文基于人工数据集和UCI数据集设计了对比实验。实验方法:针对不同数据集,将实验样本平均分成6份,任意选取其中3份作为训练样本,其他数据做测试样本,每组实验包括20个实验。实验重复做10组,取平均正确率。

最短特征线段多分类器系统中隶属度生成函数式(2)的参数λ依经验设置为λ=1。在直接设定焦元组方法的方式1和方式2中,依经验设置β=0.8。实验将对构造多分类器系统时采用不同成员分类器分类算法、不同mass函数生成方法所获取的结果进行分析比较。采用不同mass函数生成方法构造的多分类器系统及其在实验中的名称对应关系如表1所示。

表1 本文方法名称与mass函数生成方法对应表

用MCS-SFLS-Ave表示直接对隶属度求平均的融合方式,即把各成员分类器得到的隶属度的平均值作为融合隶属度,取隶属度最大的类别作为决策类别。分别用MCS-SFLS、MCS-3-NN、MCS-KNFL、MCS-NFL表示以相同的特征子空间抽取方式,分别选用SFLS、3-NN、KNFL、NFL等方法作为成员分类器分类算法生成各个成员分类器,以等权值投票方式进行融合构成多分类器系统,与新多分类器系统作对比,对数据每一维特征Fi做归一化预处理,即

(14)

3.1 人工数据集

人工数据集包含3个类别的样本,每个样本有6维互相独立的特征,每一维特征均服从高斯分布。特征的均值μ设置如表2所示,方差σ2均设为0.2。

表2 各类别样本不同特征的均值设置

实验分别选取特征1、2,特征3、4,特征5、6作为特征子空间,生成3个成员分类器构成多分类器系统。不同特征子空间上对不同类别的区分程度不同,例如由特征1、特征2构成的特征子空间对类别2的区分程度更高,如图3所示。

图3 样本在特征1、特征2子空间下的分布图

对多分类器系统在不同决策门限下进行测试,其中MCS-SFLS-Ave的融合隶属度依式(10)归一化后得到决策概率,表决融合法通过除以总票数得到决策概率,结果如表3所示。可以看出,在此数据集上,以模糊及模糊-证据融合规则构造的多分类器系统分类性能均优于表决融合的多分类器系统。

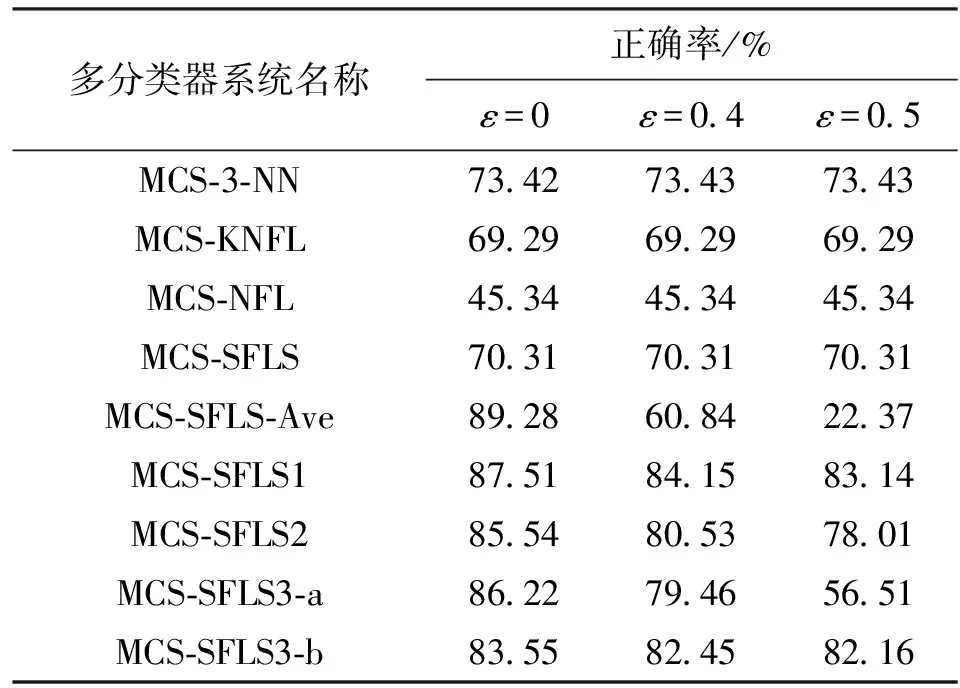
表3 人工数据集下各多分类器系统分类正确率对比

同时,从表3中可以看出,在决策门限ε=0时MCS-SFLS1和MCS-SFLS-Ave的分类性能较为突出,但是随着决策门限增大,MCS-SFLS-Ave的分类正确率下降很快,而MCS-SFLS1和MCS-SFLS2下降并不明显。这表明在高决策门限情况下,基于模糊-证据融合规则的融合方法决策正确率高于简单隶属度平均融合方法。因而,基于模糊-证据融合规则的融合结果可靠性更高。在本实验中成员分类器较少,决策门限对投票法融合结果无实质影响。

3.2 UCI数据集

实验使用到的数据集信息如表4所示。

通过选用不同的特征子空间来生成成员分类器。若样本有D维特征,则可构成2D-1个特征子空间,以此可以得到2D-1个成员分类器,从中等概率地选择5个成员分类器构成多分类器系统。决策门限均设为0.4(对二分类问题没有影响)。实验结果如表5所示。

表4 实验用UCI数据集信息

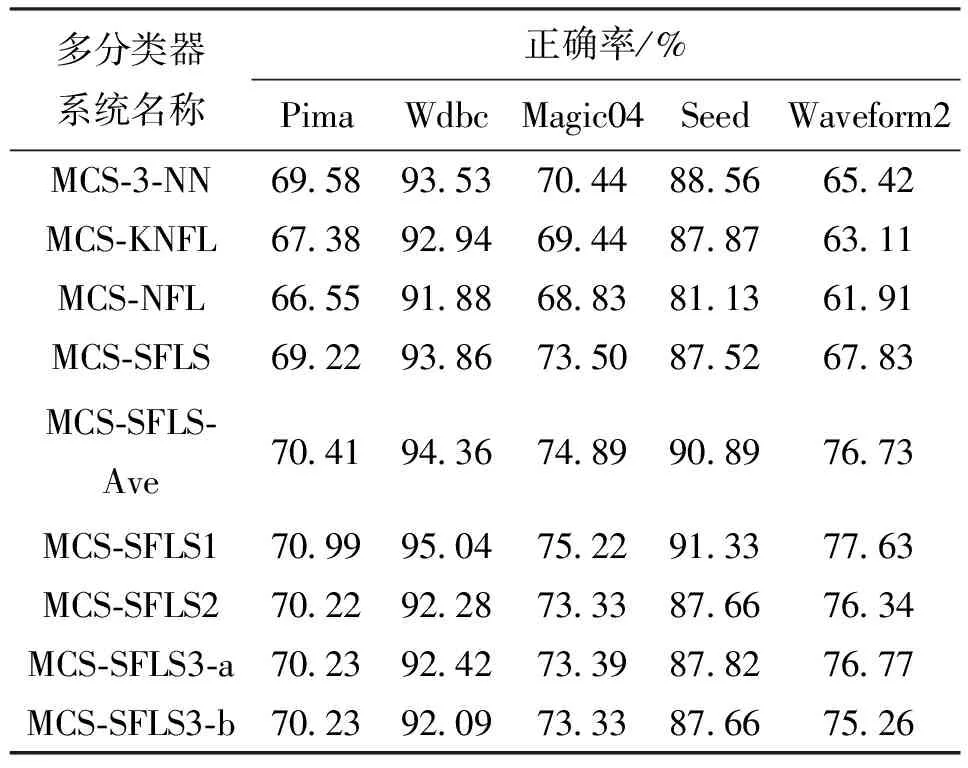
表5 不同UCI数据集下多分类器系统分类正确率对比

从实验结果可以看出,最短特征线段多分类器系统的分类性能较为理想,尤其在Seed和Waveform2数据集上,分类正确率明显高于其他多分类器系统,其中基于COWA-ER的多分类器系统(MCS-SFLS1)的分类性能明显优于其他多分类器系统。一般意义上,对于特征线分类器来说,类别数目越多,特征维度越低,穿越错分问题越突出[23]。在三分类问题的Seed和Waveform2数据集上,类别个数多于二分类,且特征维数属于中低水平,因此基于特征线的方法出现穿越错分问题较多,所以基于特征线段的多分类器系统优势较大。在二分类Wdbc数据集上,由于类别数目较少,且特征维度较高(30维),穿越错分问题并不突出,基于特征线段的多分类器系统优势相对减弱。

总体而言,本文提出的最短特征线段多分类器系统在继承了SFLS分类器良好分类性能的同时,利用模糊-证据理论方法进行融合,进一步提高了多分类器系统的分类性能。

4 结 论

本文设计了利用SFLS作为成员分类器,以模糊-证据融合规则构造的多分类器系统。将SFLS的输出改为度量级形式,进而使用证据理论实现模糊融合分类决策。实验表明,本文方法能更加充分地利用特征线段中包含的信息,相比其他基于邻域型分类器的多分类器系统而言,进一步提高了分类正确率,并且基于模糊-证据融合的识别结果比基于模糊隶属度平均方法的可靠性更高,而在各种模糊-证据融合方法中,COWA-ER性能更优。

本文研究的重点在于成员分类器个体的设计以及融合规则的设计和选取,但对于多分类器系统来说,成员分类器之间的差异性[19]更为关键。

[1] 李晶皎, 赵丽红, 王爱侠. 模式识别 [M]. 北京: 电子工业出版社, 2010.

[2] 杨艺, 韩崇昭, 韩德强. 利用特征子空间评价与多分类器融合的高光谱图像分类 [J]. 西安交通大学学报, 2010, 44(8): 20-24. YANG Yi, HAN Chongzhao, HAN Deqiang. Hyperspectral image classification based on feature subspace evaluation and multiple classifier fusion [J]. Journal of Xi’an Jiaotong University, 2010, 44(8): 20-24.

[3] 张成军, 阴妍, 鲍久圣, 等. 多源信息融合故障诊断方法研究进展 [J]. 河北科技大学学报, 2014, 35(3): 213-221. ZHANG Chengjun, YIN Yan, BAO Jiusheng, et al. Research progress in fault diagnosis methods based on multi-source information fusion [J]. Journal of Hebei University of Science and Technology, 2014, 35(3): 213-221.

[4] 王风华, 韩九强, 姚向华. 一种基于虹膜和人脸的多生物特征融合方法 [J]. 西安交通大学学报, 2008, 42(2): 133-137. WANG Fenghua, HAN Jiuqiang, YAO Xianghua. Multimodal biometric fusion approach based on iris and face [J]. Journal of Xi’an Jiaotong University, 2008, 42(2): 133-137.

[5] 张彩坡. 模糊积分及多分类器融合在医疗诊断中的应用 [D]. 天津: 天津理工大学, 2010.

[6] BREIMAN L. Bagging predictors [J]. Machine Learning, 1996, 24(2): 123-140.

[7] 焦李成, 公茂果, 王爽, 等. 自然计算、机器学习与图像理解前沿 [M]. 西安: 西安电子科技大学出版社, 2008.

[8] KIRA K, RENDELL L. A practical approach to feature selection [C]∥Proceedings of the 9th Machine Learning. Aberdeen, UK: Morgan Kaufmann Publishers, 1992: 249-256.

[9] MARKO R, IGOR K. Theoretical and empirical analysis of ReliefF and RReliefF [J]. Machine Learning, 2003, 53(1/2): 23-69.

[10]DIETTERICH T G. An experimental comparison of three methods for constructing ensembles of decision trees: bagging, boosting and randomization [J]. Machine Learning, 2000, 40(2): 139-157.

[11]梁绍一, 韩德强, 韩崇昭. 一种基于几何关系的多分类器差异性度量及其在多分类器系统构造中的应用 [J]. 自动化学报, 2014, 40(3): 449-458. LIANG Shaoyi, HAN Deqiang, HAN Chongzhao. A novel diversity measure based on geometric relationship and its application to design of multiple classifier systems [J]. Acta Automatica Sinica, 2014, 40(3): 449-458.

[12]XU Lei, KRZYZAK A, SUEN C Y. Methods of combining multiple classifiers and their applications to handwriting recognition [J]. IEEE Transactions on Systems, Man and Cybernetics, 1992, 22(3): 418-435.

[13]COVER T, HART P. Nearest neighbor pattern classification [J]. IEEE Transactions on Information Theory, 1967, 13(1): 21-27.

[14]DU Hao, CHEN Yanqiu. Rectified nearest feature line segment for pattern classification [J]. Pattern Recognition, 2007, 40(5): 1486-1497.

[15]HAN Deqiang, HAN Chongzhao, YANG Yi. A novel classifier based on shortest feature line segment [J]. Pattern Recognition Letters, 2011, 32(3): 485-493.

[16]HE Yunhui. Face recognition using kernel nearest feature classifiers [C]∥2006 International Conference on

Computational Intelligence and Security. Piscataway, NJ, USA: IEEE, 2006: 678-683.

[17]杨艺, 韩德强, 韩崇昭. 基于排序融合的特征选择 [J]. 控制与决策, 2011, 26(3): 397-401. YANG Yi, HAN Deqiang, HAN Chongzhao. Study on feature selection based on rank-level fusion [J]. Control and Decision, 2011, 26(3): 397-401.

[18]TACNET J M, DEZERT J. Cautious OWA and evidential reasoning for decision making under uncertainty [C]∥Proceeding of the 14th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2011: 1-8.

[19]SHAFER G. A mathematical theory of evidence [M]. Princeton, USA: Princeton University Press, 1967.

[20]HAN Deqiang, DEZERT J, TACNET J M, et al. A fuzzy-cautious OWA approach with evidential reasoning [C]∥Proceedings of the 15th International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2012: 278-285.

[21]VALENTE F, HERNANSKY H. Combination of acoustic classifiers based on Dempster-Shafer theory of evidence [C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Piscataway, NJ, USA: IEEE, 2007: 1129-1132.

[22]SMETS P. Data fusion in the transferable belief model [C]∥Proceedings of the 3rd International Conference on Information Fusion. Piscataway, NJ, USA: IEEE, 2000: 21-33.

[23]DU Hao, CHEN Yanqiu. Rectified nearest feature line segment for pattern classification [J]. Pattern Recognition, 2007, 40(5): 1486-1497.

(编辑 赵炜)

(1.西安交通大学智能网络与网络安全教育部重点实验室,710049,西安;2.西安交通大学机械结构强度与振动国家重点实验室,710049,西安)

为提高多分类器系统分类的性能,设计了一种使用最短特征线段分类器的多分类器系统。依据最短特征线段分类算法工作机理,利用特征线段长度表征样本隶属于各个类别的可能性,即模糊隶属度,对成员分类器输出形式完成由摘要级至度量级的重新建模,更多地保留输出细节以减少信息损失,进而利用基于模糊的证据融合规则实现成员分类器的度量级融合,通过隶属度到mass函数的转换,利用模糊-证据融合规则实现多分类器系统的构造,进一步提高了多分类器系统分类性能。采用人工数据集和UCI数据集设计了对比实验,实验表明,与其他邻域型分类器构造的多分类器系统相比,新多分类器系统能有效提升分类正确率。

特征线段;隶属度;多分类器系统;证据理论

Design of Multiple Classifier Systems Based on Shortest Feature Line Segment

DING Jiankun1,HAN Deqiang1,YANG Yi2

(1. Ministry of Education Key Lab for Intelligent Networks and Network Security, Xi’an Jiaotong University, Xi’an 710049, China; 2. State Key Laboratory of Strength and Vibration, Xi’an Jiaotong University, Xi’an 710049, China)

To improve the classification performance of multiple classifier systems, a novel multiple classifier system using shortest feature line segment (SFLS) as member classifiers is proposed. According to the SFLS’s algorithmic principle on classification, the length of the shortest feature line segment is used to represent the probability, i.e., the fuzzy membership of the query sample belonging to the corresponding class. Thus, the member classifier’s output is transformed from the abstract level to the measurement level. Furthermore, by transforming the fuzzy membership function into the mass function and using fuzzy-based evidential fusion rules, the classification fusion is implemented. Compared with traditional multiple classifier systems, the proposed approach can use more detailed information for implementing more effective decision-level fusion. Experimental results show that the proposed multiple classifier systems can effectively improve classification accuracy.

feature line segment; membership function; multiple classifier systems; evidence theory

2015-01-28。 作者简介:丁建坤(1990—),男,博士生;韩德强(通信作者),男,副教授,博士生导师。 基金项目:国家“973计划”资助项目(2013CB329405);国家自然科学基金资助项目(61203222);教育部博士点基金资助项目(20120201120 036);中央高校基本科研业务费专项资金资助项目(xjj2012104,xjj2014122)。

时间:2015-07-10

http:∥www.cnki.net/kcms/detail/61.1069.T.20150710.1032.001.html

10.7652/xjtuxb201509014

TP391

A

0253-987X(2015)09-0077-07