应用热弹塑性理论的结合部法向载荷分形模型
冯燕,俞小莉,刘震涛
应用热弹塑性理论的结合部法向载荷分形模型
冯燕1,2,俞小莉1,刘震涛1
粗糙表面接触特性参数是影响机械产品静、动态特性的关键因素,而法向接触刚度与法向接触载荷是机械结构静态特性研究的重要内容,且法向载荷对接触刚度具有明显影响[1]。早先基于实验统计学参数建立的接触模型,由于基础数据受测试仪器和样本限制,其计算结果具有不确定性[2]。工程表面大多具有分形特征,应用分形理论对结合部的接触行为进行研究,是接触理论发展的必然趋势[3]。针对结合部法向接触载荷,Goerke[4]、温淑花[5]、Jiang[6]、兰国生[7]、宿月文[8]、田红亮[9-10]等学者先后进行了一些研究。但是,这些研究都局限于纯机械领域,没有考虑结合部温度及热应力变化带来的影响,而实际工作中,以内燃机为代表的机械产品往往处于变化着的热环境中,温度变化对接触情况的影响是不容忽视的。
目前,温度因素对弹塑性接触力学行为的影响仍缺乏研究。刘天祥等建立了考虑屈服点温度相关效应的粗糙表面热弹塑性接触无网格法数值计算模型,但该研究受限于仪器分辨率和采样长度[11]。
综合考虑以上情况,本文基于各向异性分形几何理论的法向接触载荷模型[9](以下简称TZQ模型),将其与热弹塑性接触理论建立的粗糙表面热力学特性相结合,引入机械载荷比例系数,建立了一种新的热弹塑性接触法向载荷分形模型,并分析了结合部温差对热弹塑性接触法向载荷的影响规律。
1 建立模型
机械结构的固定结合部问题从本质上来说是两个粗糙表面的接触问题,可简化为粗糙表面与刚性平面的接触[6],如图1所示。从微观上说,粗糙表面存在大量微凸体,接触仅发生在微凸体上。因此,研究结合部整体的法向载荷问题,需要以单个微凸体的热弹塑性接触研究为基础。

图1 单个微凸体与刚性平面的接触示意图
1.1 单个微凸体热弹塑性接触的法向载荷
机械零部件之间一般通过螺栓、螺钉、销钉、键等方式连接,当所处环境温度发生变化或接触的两个零部件之间受热状况改变时,由于受原本连接的约束限制,在两个接触面间就会产生热应力。热应力问题与无热载荷的应力分析问题相比,除了增加一项以初应变形式出现的温度载荷外,其他完全相同。所以,可以将单个微凸体承受的法向载荷p分为机械载荷pm和由热应力引起的载荷pt,即p=pm+pt。
在弹性变形阶段,单个微凸体承受的法向弹性载荷
(1)
式中:由热应力引起的法向载荷pte=σae,其中σ为由热应力引起的单个微凸体微接触截面上所承受的压应力,ae为弹性变形阶段单个微凸体的实际微接触截面积。在接触过程中,根据热应力概念,σ=αE′ΔT[12],所以
(2)

(3)
根据文献[9],单个微凸体承受的法向弹性机械载荷
(4)
将式(2)~式(4)代入式(1),得到考虑热应力时单个微凸体承受的法向弹性载荷
(5)
在塑性变形阶段,单个微凸体承受的法向塑性载荷
(6)
同理,由热应力引起的法向载荷
(7)
式中:ap为塑性变形阶段单个微凸体的实际微接触截面积,此时ap与单个微凸体微接触截面积a′的关系为[9]
(8)
由文献[9]可知,单个微凸体承受的法向塑性机械载荷
(9)
式中:K为硬度与屈服强度之比,称为相关因子,K=H/σy,其中H为较软材料的硬度,σy为较软材料的屈服强度。
将式(7)~式(9)代入式(6),得到考虑热应力时单个微凸体承受的法向塑性载荷
(10)
为给出结合部热弹塑性接触问题法向载荷分形模型的另一种更简洁的表达形式,引入机械载荷比例系数。若pte≠0,ptp≠0,设pme=f1αE′ΔTa′,pmp=f2αE′ΔTa′,其中f1为弹性变形阶段机械载荷相比于热载荷的比例系数(f1≠0),f2为塑性变形阶段机械载荷相比于热载荷的比例系数(f2≠0),比例系数越大则机械载荷占总载荷的比值越大。需要说明的是,f1和f2分别为弹、塑性变形阶段某一特定情况下的比例系数,其值可能会随着工况变化而改变。包含机械载荷比例系数的单个微凸体承受的法向弹、塑性载荷分别为
(11)
(12)
1.2 整体热弹塑性接触的法向总载荷
微凸体微接触截面积的分布函数为[9]
(13)

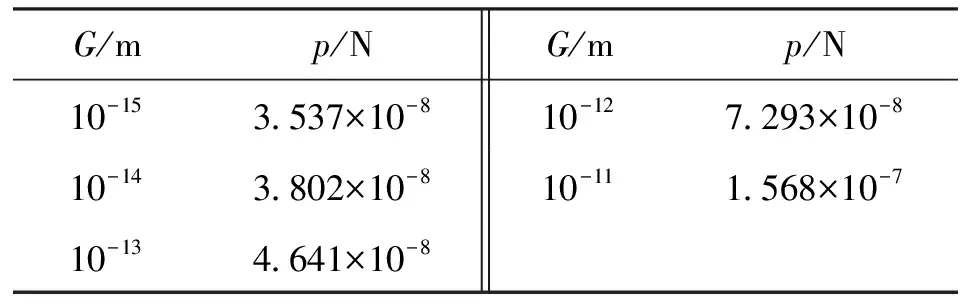
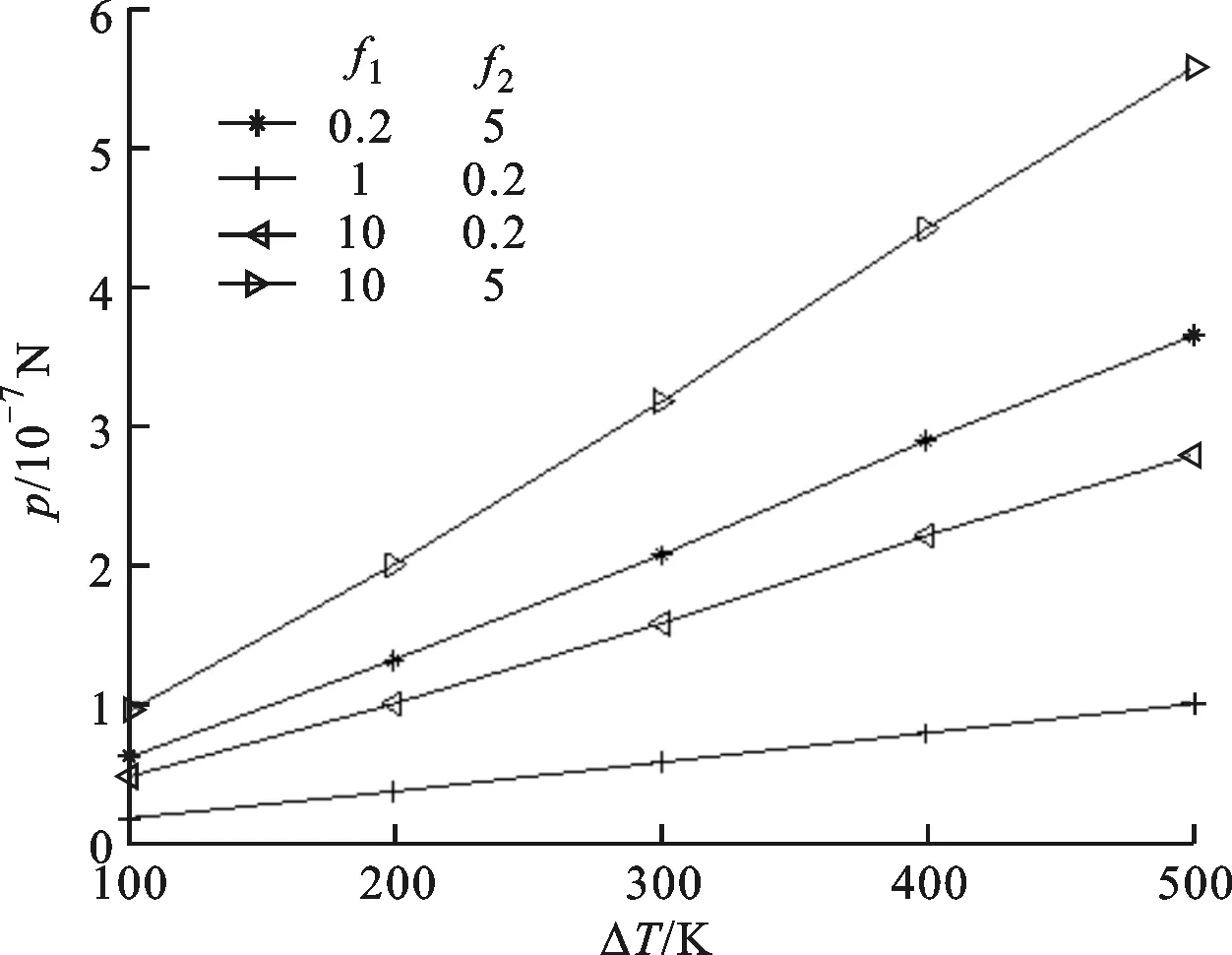
1 (14) 其定义域不同于文献[9]中式(46)的定义域,因为D=1时,图形不具备分形特征;D=2时,Ψ可取任意值,没有意义。图2为给定D的取值、根据信赖域反射算法绘制出的D-Ψ曲线。 图2 D-Ψ曲线 (15) 将式(5)、(10)、(13)代入式(15),可求得整体热弹塑性接触的法向总载荷。 当D≠1.5时 (16) 式中 当D=1.5时 (17) 式中 将式(11)~式(13)重新代入式(15),得到考虑机械载荷比例系数的整体热弹塑性接触法向总载荷的表达式 (18) 需要强调的是:式(16)、(17)和式(18)是整体热弹塑性接触法向总载荷的两种不同的表达形式,与文献[5,7,9]中模型的最大不同之处在于,式(16)、(17)和式(18)中包含了结合部的温度变化量ΔT,能反映温度变化对接触部位整体法向总载荷的影响。 当α=0或ΔT=0时,pte=0,ptp=0,此时仅存在机械载荷,式(18)没有意义。除此之外,式(18)都适用。作为结合部热弹塑性接触问题法向载荷分形模型的另一种表达形式,式(18)的意义和好处是提供了另一种计算和分析的方法,相比于不包含机械载荷比例系数的模型,它更简洁,计算更方便。然而,式(18)仅适用于考虑热应力的情况,对于纯机械的情况并不适用,在应用范围上,与常见的纯机械载荷情况下接触问题的经典分形模型(如TZQ模型)互不包含,且没有交集。从建模过程可以看出,不论是否存在热载荷,描述结合部整体热弹塑性接触法向总载荷的式(16)、(17)都适用。 以下通过特例来验证本文所建模型的有效性。 当α=0时,热载荷为0,代入式(16)、(17)可得到仅存在机械载荷时结合部的整体法向总载荷。 当D≠1.5时 (19) 当D=1.5时 (20) 当ΔT=0时,也不存在热载荷,将其代入式(16)、(17),可以得到同样的结果。 式(19)、(20)即文献[9]中不考虑热应力的结合部整体法向总载荷的经典模型。 下面将本文模型的计算结果与不考虑热应力的TZQ模型的计算结果进行对比和分析。 3.1 两铸铁接触 在工程机械的静摩擦接触范畴内,广泛存在铸铁-铸铁接触副,本节以此为例进行对比计算。 表1 两铸铁接触的整体法向总载荷(TZQ模型) 由于材料的弹性模量和线膨胀系数会随温度升高而改变,故参照铸铁的变物性参数取值,选用在不同工作温度下的弹性模量与线膨胀系数,其余参数取值同上。以实际工作中两铸铁材料结合部最常见的0—500 K温差为变量范围,得到整体热弹塑性接触法向总载荷随ΔT变化的关系曲线,如图3所示,图中各条线均为曲率很小的曲线。各条线的起点,即ΔT=0时的p值,就是表1中TZQ模型的计算结果。为增强对比效果,以G=10-11m时TZQ模型的计算结果为代表,同时考虑材料弹性模量的变物性特点,通过计算,在图3中添加了反映该结果的曲线。 图3 两铸铁接触的计算结果对比 3.2 铸铁-不锈钢接触 在内燃机中,缸盖与机体常采用铸铁材料,与之接触的缸垫材料常为不锈钢,故本节以铸铁与不锈钢接触为例进行对比计算。 当ΔT=0时,取E′=6.5×1010Pa,α=1.13×10-5K-1,K=0.4,σy=2.5×108Pa。对应不同的G值,根据TZQ模型计算得到的铸铁-不锈钢接触整体法向总载荷见表2。 表2 铸铁-不锈钢接触的法向总载荷(TZQ模型) 选用不同工作温度下铸铁和不锈钢的弹性模量与线膨胀系数,其余参数同上,采用本文模型和TZQ模型分别计算,得到了铸铁-不锈钢接触的法向载荷,见图4。图中各条线的起点,即是表2中TZQ模型的计算结果。 图4 铸铁-不锈钢接触的计算结果对比 通过以上两个实例可见,即便考虑变物性参数的影响,TZQ模型的计算结果受ΔT变化的影响仍很小,且随着温差增大,与本文模型间的计算结果差距增大。这是因为TZQ模型没有考虑结合部温度变化产生的热载荷对计算结果带来的影响,在温差显著增大的情况下,其计算结果不符合客观预期。 采用考虑机械载荷比例系数的热弹塑性接触法向载荷分形模型,假设机械载荷比例系数不随ΔT改变,研究温差对热弹塑性接触法向总载荷p的影响规律。 图5 温差ΔT对法向总载荷p的影响曲线 由数字仿真计算结果可见,热弹塑性接触法向总载荷随着结合部温差的增大而增大,且比例系数f1、f2越大,法向总载荷增大的幅度也越大。在图5所示的4组数据中,在其他参数相同的情况下,当f1=1、f2=0.2时,得到的法向总载荷最小。这是因为结合部温差增大导致微凸体的变形也增大,继而使热弹塑性接触法向总载荷增大。 (1)本文建立的不包含机械载荷比例系数的结合部热弹塑性接触问题法向载荷分形模型,既适用于考虑热应力的情况,也适用于纯机械情况,是传统纯机械模型在基础理论和应用范围上的扩展。 (2)本文建立的考虑机械载荷比例系数的热弹塑性接触问题法向载荷分形模型,仅适用于考虑热应力的情况,作为模型的另一种表达形式,提供了另一种计算和分析的方法,其形式更简洁,计算更方便。 (3)热弹塑性接触法向载荷随着结合部温差的增大而增大。 (4)本文基于热弹塑性接触的结合部法向载荷分形模型综合考虑了温差、接触材料线膨胀系数、机械载荷比例系数等参数的影响,从而可用于计算和分析工程实际中大量存在的结合部温度发生改变的接触情况,其结果更符合客观预期。 参考文献: [1] 尤晋闽, 陈天宁. 结合面法向动态参数的分形模型 [J]. 西安交通大学学报, 2009, 43(9): 91-94. YOU Jinmin, CHEN Tianning. Fractal model for normal dynamic parameters of joint surfaces [J]. Journal of Xi’an Jiaotong University, 2009, 43(9): 91-94. [2] GREENWOOD J A, WILLIMSON J B P. Contact of nominally flat surfaces [J]. Proc R Soc Lond: A, 1996, 295(1442): 300-319. [3] 姬翠翠, 朱华. 粗糙表面分形接触模型的研究进展 [J]. 润滑与密封, 2011, 36(9): 114-119. JI Cuicui, ZHU Hua. Research progress on M-B fractal contact model [J]. Lubrication Engineering, 2011, 36(9): 114-119. [4] GOERKE D, WILLNER K. Normal contact of fractal surfaces [J]. Wear, 2008, 264(7): 589-598. [5] 温淑花, 张学良, 武美先, 等. 结合面法向接触刚度分形模型建立与仿真 [J]. 农业机械学报, 2009, 40(11): 197-202. WEN Shuhua, ZHANG Xueliang, WU Meixian, et al. Fractal model and simulation of normal contact stiffness of joint interfaces and its simulation [J]. Transactions of the Chinese Society of Agricultural Machinery, 2009, 40(11): 197-202. [6] JIANG Shuyun, ZHENG Yunjian, ZHU Hua. A contact stiffness model of machined plane joint based on fractal theory [J]. ASME Journal of Tribology, 2010, 132: 011401. [7] 兰国生, 张学良, 丁红钦, 等. 基于分形理论的结合面改进接触模型 [J]. 农业机械学报, 2011, 42(10): 217-223. LAN Guosheng, ZHANG Xueliang, DING Hongqin, et al. Modified contact model of joint interfaces based on fractal theory [J]. Transactions of the Chinese Society of Agricultural Machinery, 2011, 42(10): 217-223. [8] 宿月文, 陈渭, 朱爱斌, 等. 分形特征表面接触磨损模拟 [J]. 西安交通大学学报, 2013, 47(7): 52-56. SU Yuewen, CHEN Wei, ZHU Aibin, et al. Contact and wear simulation between fractal surfaces [J]. Journal of Xi’an Jiaotong University, 2013, 47(7): 52-56. [9] 田红亮, 钟先友, 秦红玲, 等. 依据各向异性分形几何理论的固定结合部法向接触力学模型 [J]. 机械工程学报, 2013, 49(21): 108-122. TIAN Hongliang, ZHONG Xianyou, QIN Hongling, et al. Normal contact mechanics model of fixed joint interface adopting anisotropic fractal geometrical theory [J]. Chinese Journal of Mechanical Engineering, 2013, 49(21): 108-122. [10]田红亮, 陈从平, 方子帆, 等. 应用改进分形几何理论的结合部切向刚度模型 [J]. 西安交通大学学报, 2014, 48(7): 46-52. TIAN Hongliang, CHEN Congping, FANG Zifan, et al. Tangential stiffness model for joint interface adopting the revised fractal geometric theory [J]. Journal of Xi’an Jiaotong University, 2014, 48(7): 46-52. [11]刘天祥, 刘更, 谢琴, 等. 粗糙表面热弹塑性接触问题的无网格法 [J]. 机械工程学报, 2009, 45(1): 20-26. LIU Tianxiang, LIU Geng, XIE Qin, et al. Mesh-free method for thermal elasto-plastic contact of rough surfaces [J]. Chinese Journal of Mechanical Engineering, 2009, 45(1): 20-26. [12]肖永宁, 潘克煜, 韩国埏. 内燃机热负荷和热强度 [M]. 北京: 机械工业出版社, 1988: 162. [13]成大先. 机械设计手册: 第1卷 [M]. 北京: 化学工业出版社, 2008: 38. [本刊相关文献链接] 褚坤明,王家序,蒲伟,等.混合润滑状态下滤波减速器的啮合冲击分析与修形方法.2015,49(7):140-148.[doi:10.7652/xjtuxb201507023] 周安安,陈天宁,王小鹏,等.自仿射接触点及其在分形接触理论中的应用.2015,49(6):8-15.[doi:10.7652/xjtuxb2015 06002] 陈卫华,陈天宁,王小鹏,等.纤维多孔金属的流阻率分形模型研究.2015,49(6):132-137.[doi:10.7652/xjtuxb201506 021] 陈兵奎,梁栋,彭帅,等.共轭曲线齿轮啮合管齿面的几何及接触特性分析.2015,49(3):85-94.[doi:10.7652/xjtuxb 201503015] 田红亮,赵美云,郑金华,等.新的柔性结合部法向接触刚度和接触阻尼方程.2015,49(1):118-126.[doi:10.7652/xjtuxb201501020] 田红亮,陈从平,方子帆,等.应用改进分形几何理论的结合部切向刚度模型.2014,48(7):46-52.[doi:10.7652/xjtuxb 201407009] 宿月文,陈渭,朱爱斌,等.分形特征表面接触磨损模拟.2013,47(7):52-56.[doi:10.7652/xjtuxb201307010] 田红亮,赵春华,朱大林,等.整个螺栓结合部的法向连接动刚度及试验验证.2012,46(9):31-36.[doi:10.7652/xjtuxb201209007] 方兵,张雷,赵继,等.轴承结合部动态参数识别与等效分析模型的研究.2012,46(11):69-74.[doi:10.7652/xjtuxb2012 11014] 张学良,温淑花,兰国生,等.平面结合面切向接触阻尼分形模型及其仿真.2011,45(5):74-77.[doi:10.7652/xjtuxb 201105014] 尤晋闽,陈天宁.结合面法向动态参数的分形模型.2009,43(9):91-94.[doi:10.7652/xjtuxb200909020] (编辑 葛赵青) (1.浙江大学动力机械及车辆工程研究所,310027,杭州;2.浙江同济科技职业学院机电系,311231,杭州) 针对现有法向接触载荷分形模型没有考虑热应力的影响、不适用于结合部温度变化的问题,基于热弹塑性理论和接触分形理论,建立了热弹塑性接触法向载荷分形模型。该模型是对传统模型在基础理论和应用范围上的拓展,综合考虑了温差、线膨胀系数、机械载荷比例系数等参数的影响,从而可用于计算和分析工程实际中大量存在的结合部温度发生改变的接触情况,其结果更符合客观规律。此外,针对考虑热应力的接触问题,引入机械载荷比例系数,给出了模型的另一种表达形式。通过特例验证了模型的有效性,并与前人的模型进行了对比分析,结果显示:模型间的计算结果差距随结合部温差的增大而增大。最后,通过数字仿真揭示了结合部温差对热弹塑性接触法向载荷的影响规律——热弹塑性接触法向载荷随结合部温差的增大而增大。 热弹塑性;法向接触载荷;结合部;比例系数;分形模型 A Normal Load Fractal Model of Joint Interface Based on Thermal Elasto-Plastic Theory FENG Yan1,2,YU Xiaoli1,LIU Zhentao1 (1. Power Machinery & Vehicular Engineering Institute, Zhejiang University, Hangzhou 310027, China; 2. Department of Mechanical and Electrical Engineering, Zhejiang Tongji Vocational College of Science and Technology, Hangzhou 311231, China) Without considering the influence of heat, the existing fractal contact models are not applicable to analyze the contact issues when the temperature changes. Based on thermal elasto-plastic theory and contact fractal theory, a new fractal model of normal contact load is established in this study. This model expands the basic theory and applications of traditional models, and comprehensively considers the effects of such parameters as temperature difference, linear expansion coefficient, mechanical load scale factor, etc. Therefore this model can help calculate and analyze the real contact conditions between fixed contact surfaces when the temperature changes, and it shows better conformity with objective laws. Besides, another expression of the model is proposed by introducing mechanical load scale factor. Then the model is validated through a special case, and comparative study is conducted between this model and TZQ model. The results show that the difference between the model calculations increases with the junction temperature difference. In addition, the effect of temperature difference on the normal contact load is also analyzed. The results reveal that the normal contact load of thermal elasto-plastic contact increases with the temperature difference at joint interface. thermal elasto-plastic; normal contact load; joint interface; scale factor; fractal model 2015-01-15。 作者简介:冯燕(1985—),女,博士生,浙江同济科技职业学院讲师;刘震涛(通信作者),男,副教授。 基金项目:国家高技术研究发展计划资助项目(2012AA111709)。 时间:2015-06-19 http:∥www.cnki.net/kcms/detail/61.1069.T.20150619.1649.002.html 10.7652/xjtuxb201509004 TH123 A 0253-987X(2015)09-0018-06
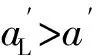


2 特例验证
3 计算结果对比与分析




4 温差对法向总载荷的影响
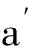
5 结 论

