非均匀载荷下厚壁圆筒稳态蠕变应力的计算

王建梅,苗克军,徐俊良,李璞



非均匀载荷下厚壁圆筒稳态蠕变应力的计算

王建梅,苗克军,徐俊良,李璞

厚壁圆筒是工程中的重要结构,广泛应用于化工、核电、军工、冶金等领域[1],长期在高温(0.3Tm以上,Tm为熔点)和复杂载荷下工作时需要考虑蠕变过程[2]。关于在均匀载荷下稳态蠕变应力的求解问题,Naumenko等分析了蠕变对厚壁圆筒平面应力的影响[3],Boyle基于von Mises屈服准则,得到了厚壁圆筒的等效应力解析解[4]。然而,在工程中经常遇到的是非均匀载荷的情况[5]。关于厚壁圆筒在非均匀载荷下的弹性问题的应力求解,吴庆良等采用复变函数法计算了外表面承受非均匀载荷作用时厚壁圆筒的平面应力[6],郑俊德等利用应力函数法获得了厚壁圆筒的应力解析解[7]。上述研究虽然给出了一些厚壁圆筒平面应力的解析求解方法,但均未考虑在蠕变条件下受非均匀载荷厚壁圆筒的应力求解问题,且国内尚无相关文献介绍这方面的研究。

本文以厚壁圆筒为研究对象,利用多维应力下稳态蠕变的基础理论与厚壁圆筒平面应力的计算方法,推导出一类在外边界固定、内边界受非均匀载荷情况下的稳态蠕变应力计算公式,提出了一种多维应力蠕变的计算方法,应用所得公式分析了工程中油膜轴承衬套的蠕变应力,并以蠕变试验为基础,模拟了衬套的蠕变过程。

1 理论计算

1.1 算法推导

为计算承受非均匀内压的厚壁圆筒的稳态蠕变应力,本文主要考虑第二阶段的蠕变,即稳态蠕变。在稳态蠕变阶段,不考虑温度对蠕变应力的影响时,弹性力学中的平衡方程、协调方程、几何方程、边界方程等仍然适用[8]。同时,假设圆筒处于平面应力状态,即σz=0,对厚壁圆筒的中间截面进行应力分析。

设定一个内半径为a、外半径为b的厚壁圆筒,其外边界(r=b)固定,内边界(r=a)受到非均匀径向压力p(θ)的作用,计算模型如图1所示。

图1 厚壁圆筒计算模型示意图

(1)

式中:am为与压力相关的系数;m和n为整数,且m≤n。

边界条件为

(2)

式中:ur和vθ为位移分量。

根据几何形状和边界载荷选取应力函数[9]

(3)

式中:Am、Bm、Cm和Dm为未知参数。

σr、σθ和τrθ为应力分量,表达式为

(4)

将式(3)代入式(4)得

(5)

对于多维稳态蠕变应力分析,将等效应力和等效蠕变分别定义为多维应力下的应力分量和蠕变应变分量,以诺顿稳态蠕变公式为基础,得到如下稳态蠕变的平面应力应变关系[10]

(6)

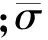
将式(5)代入式(6)得

(7)

几何方程[9]为

(8)

将式(7)代入式(8),并对前两项积分,得

(9)

式中:f1(θ)和f2(r)-∫f1(θ)dθ是积分常量。

将式(9)代入式(8)中的第3个式子,根据位移单值条件得

(10)

将式(10)代入式(9),并将边界条件代入式(5)和式(9),得

(11)

式中

Am={3a2+m[-5a2mb2+3a2b2mm-3b2m+2(1+

m)]am}/{2(1+m)[15a2+4mb2+15a2b2+4m+

2a2mb2m+2(9a2+8b2)+9a2mb2m(a2-b2)2m2]}

(12)

Bm={a2+mb2[15a2+2mm-9a2b2m(-m+m2)+

b2m+2(16+9m2)]am}/{2(-m+m2)[15a2+4mb2+

15a2b2+4m+2a2mb2m+2(9a2+8b2)+

9a2mb2m(a2-b2)2m2]}

(13)

Cm={3a2+mb2m[5b2+2m+3a2mb2(1-m)+

3a2m+2m]am}/{2(-1+m)[15a2+4mb2+15a2b2+4m+

2a2mb2m+2(9a2+8b2)+9a2mb2m(a2-b2)2m2]}

(14)

Dm={a2+mb2+2m[-15a2b2mm-9a2m+2(m+

m2)+a2mb2(16+9m2)]am}/{2(m+m2)·

[15a2+4mb2+15a2b2+4m+2a2mb2m+2(9a2+

8b2)+9a2mb2m(a2-b2)2m2]}

(15)

将式(12)～式(15)代入式(5),可得非均匀内压下厚壁圆筒的稳态蠕变应力分量

(16)

1.2 非均匀载荷下厚壁圆筒的蠕变应力分析

当机械零部件的温度超过材料的蠕变温度时,均应按照蠕变设计准则来确定设计用的许用应力,本文采用第四强度理论[10-11]进行判断。设计中应使零部件的最大工作应力满足如下关系式

(17)

式中:[σ]c为蠕变许用应力,由不同零部件的工作要求决定。厚壁圆筒的最大蠕变应力应该满足式(17)。

由式(16)可以看出,各应力分量由余弦函数叠加得到,考虑到每一叠加项的蠕变分布规律类似,且叠加不改变蠕变应力的分布规律,故只取其叠加项中的第一项进行分析。

考虑到上述计算模型中影响稳态蠕变应力的主要几何参数有厚壁圆筒的外半径b和内半径a以及任意一点处的半径r,因此,设定K为厚壁圆筒外半径与内半径之比:K=b/a。均匀选择厚壁圆筒的10个位置(a≤r≤b),得到其在不同K值下的蠕变应力,如图2所示。

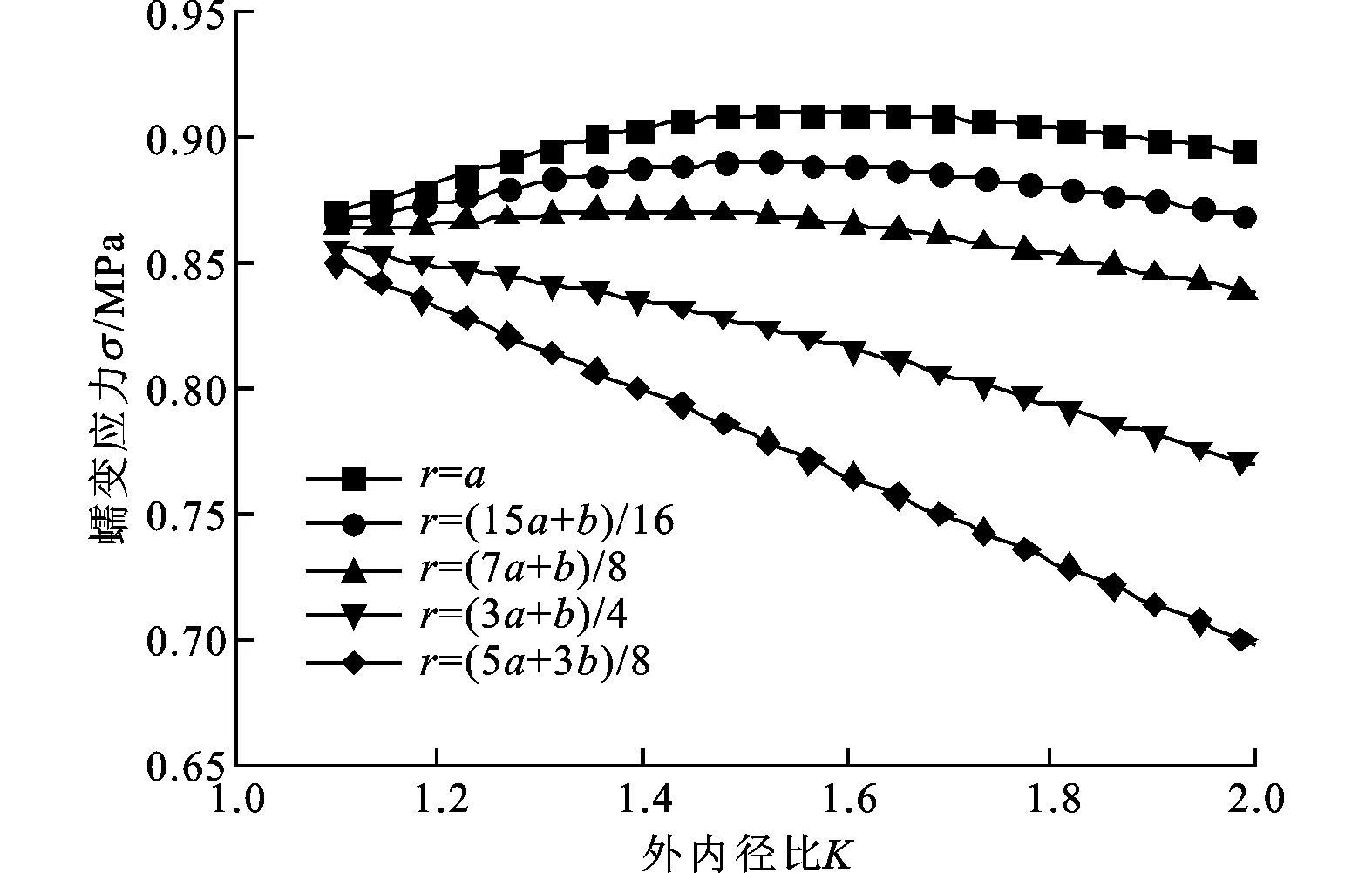
(a)a≤r≤(5a+3b)/8

(b)(a+b)/2≤r≤b图2 不同K值下厚壁圆筒的蠕变应力分布

由图2a可知,当r≤(5a+3b)/8时,半径越小,则蠕变应力随着K值增大呈现出的先增大后减小的趋势越明显。由图2b可知:随着K值增大,蠕变应力在半径r=(a+b)/2处近似线性递减;当r>(a+b)/2时,半径越大,则蠕变应力随着K值的增大而减小的速率变得越缓慢。当K值一定时,随着半径的增大,厚壁圆筒的蠕变应力逐渐降低,说明最大蠕变应力出现在内边界上;厚壁圆筒的最大蠕变应力随着K值的增加呈现出先增大后减小的规律,在K=1.58时蠕变应力最大。

2 油膜轴承衬套的蠕变应力计算

油膜轴承最薄弱的零件就是衬套中的巴氏合金,蠕变是其失效的一种形式[12]。油膜轴承衬套在工作过程中长期承受油膜压力与高温的作用,会产生微观蠕变,导致对油膜轴承的润滑性能和寿命产生不可忽略的负面影响,因此,轴承中巴氏合金的蠕变不可忽略[13]。工程中油膜轴承衬套的外边界是固定的,内边界承载区120°范围内承受径向非均匀油膜压力的作用。选择某工况下衬套内边界轴向承受油膜压力最大的中间截面,截面内周向油膜压力可用余弦函数表示

(18)

式中:poil(θ)为油膜轴承衬套内壁所受的径向油膜压力,MPa;θ为与水平方向的夹角;bm为油膜压力相关系数,其值见表1。衬套内半径为110 mm,外半径为128 mm,K=1.16。

表1 油膜压力相关系数

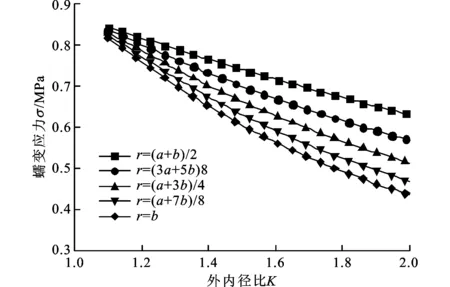
将油膜轴承衬套的相关参数代入式(16)与式(17)中,得到其承载区的蠕变应力分布,如图3所示。

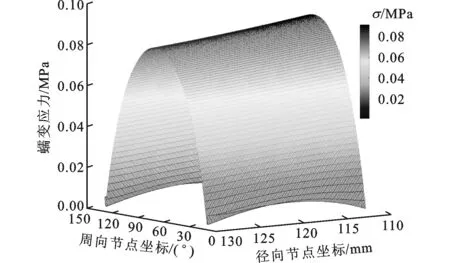
图3 油膜轴承衬套的蠕变应力分布

由图3可知:在周向,衬套的蠕变应力随着周向节点坐标的增加呈现先增大后减小的形态分布;在径向,衬套的蠕变应力随着半径的增大而减小。这表明,衬套所受载荷越大的区域,蠕变应力也越大。

3 蠕变试验

3.1 试验过程

采用有限元分析软件ANSYS求解蠕变时,所需的蠕变参数由单轴蠕变拉伸试验确定[14]。为求得衬套内壁材料的蠕变参数,针对衬套内壁材料的性能要求,在原有WDW-E100D型电子式万能试验机的基础上,设计了一套满足国家标准[15]要求的蠕变试验设备,增加了应变测量、加热、保温和控温的功能。试验所用试件如图4所示,试验设备如图5所示。选择13 MPa-60 ℃、18 MPa-60 ℃和20 MPa-60 ℃ 3种工况进行蠕变试验,根据蠕变试验数据绘制3种工况下的蠕变速率曲线,如图6所示,根据蠕变试验结果计算的稳态蠕变速率值见表2。

图4 蠕变试验试件

图5 蠕变试验设备

载荷/MPa131820稳态蠕变速率/10-10s-10 9722 8134 444

图6 蠕变速率曲线

3.2 诺顿稳态蠕变本构方程

利用ANSYS计算稳态蠕变的诺顿公式为

(19)

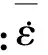
不考虑温度变化对蠕变应力的影响,即c3=0,则式(19)变为

(20)

对式(20)两边取对数,得

(21)

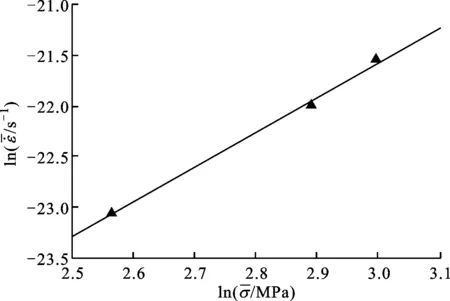
图7 等效蠕变速率与等效蠕变应力的关系

4 有限元模拟

根据油膜轴承衬套的实际尺寸,采用ANSYS建立二维模型。为提高求解精度,应用隐式蠕变算法,选择单元求解能力强且支持隐式蠕变算法的PLANE183单元,将诺顿蠕变系数输入ANSYS中。考虑衬套的实际受载情况,外边界施加周向与径向位移约束,内边界承载区120°范围内施加径向载荷。ANSYS求解结果如图8所示。

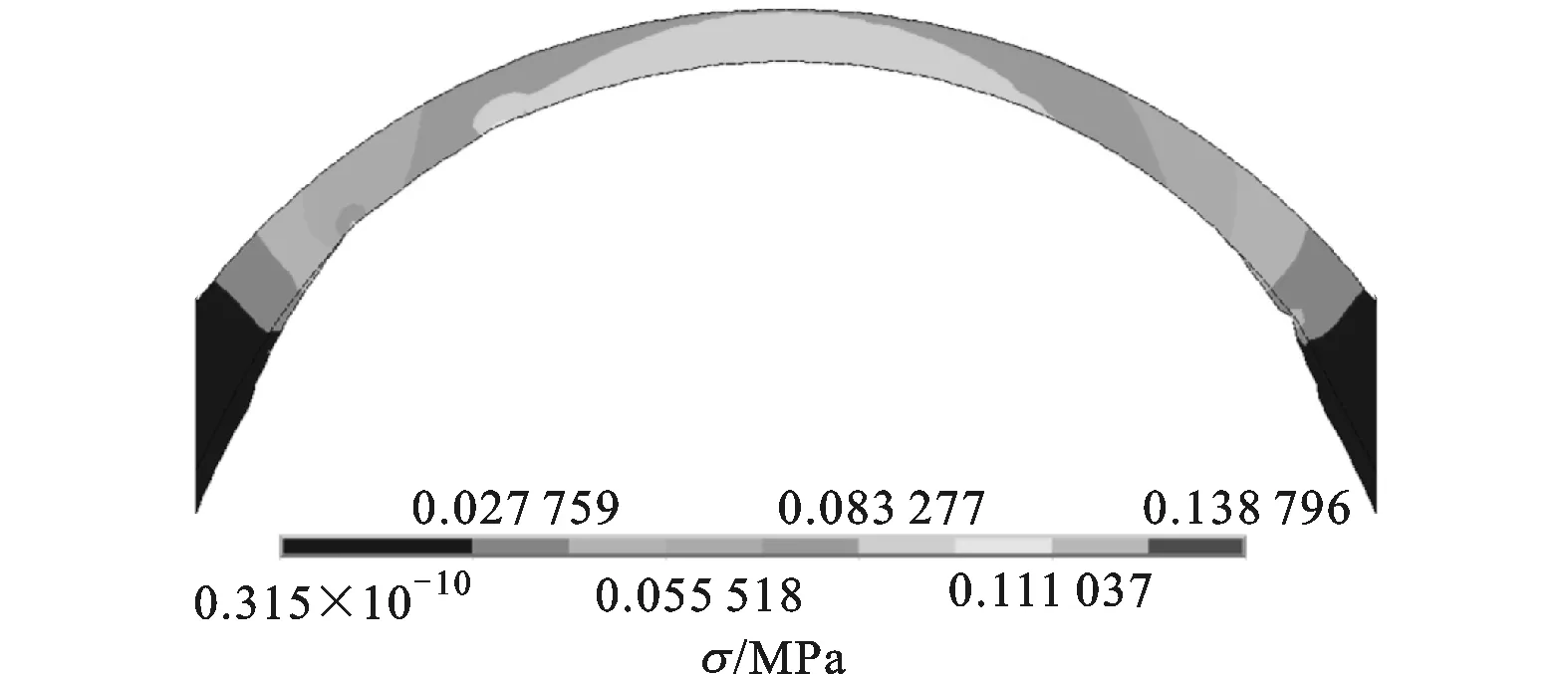
图8 承载区蠕变应力云图

由图8可知:衬套周向的应力随着载荷的增大而增大;在衬套承受的最小油膜压力处,蠕变应力接近于0,表明在油膜压力为0的地方,衬套基本不存在蠕变;在承受最大油膜压力处,蠕变应力最大,衬套蠕变最明显;蠕变应力随着半径的增大而减小,表明衬套在非承载区的蠕变不明显。模拟结果与第2节中本文方法所得结果一致。

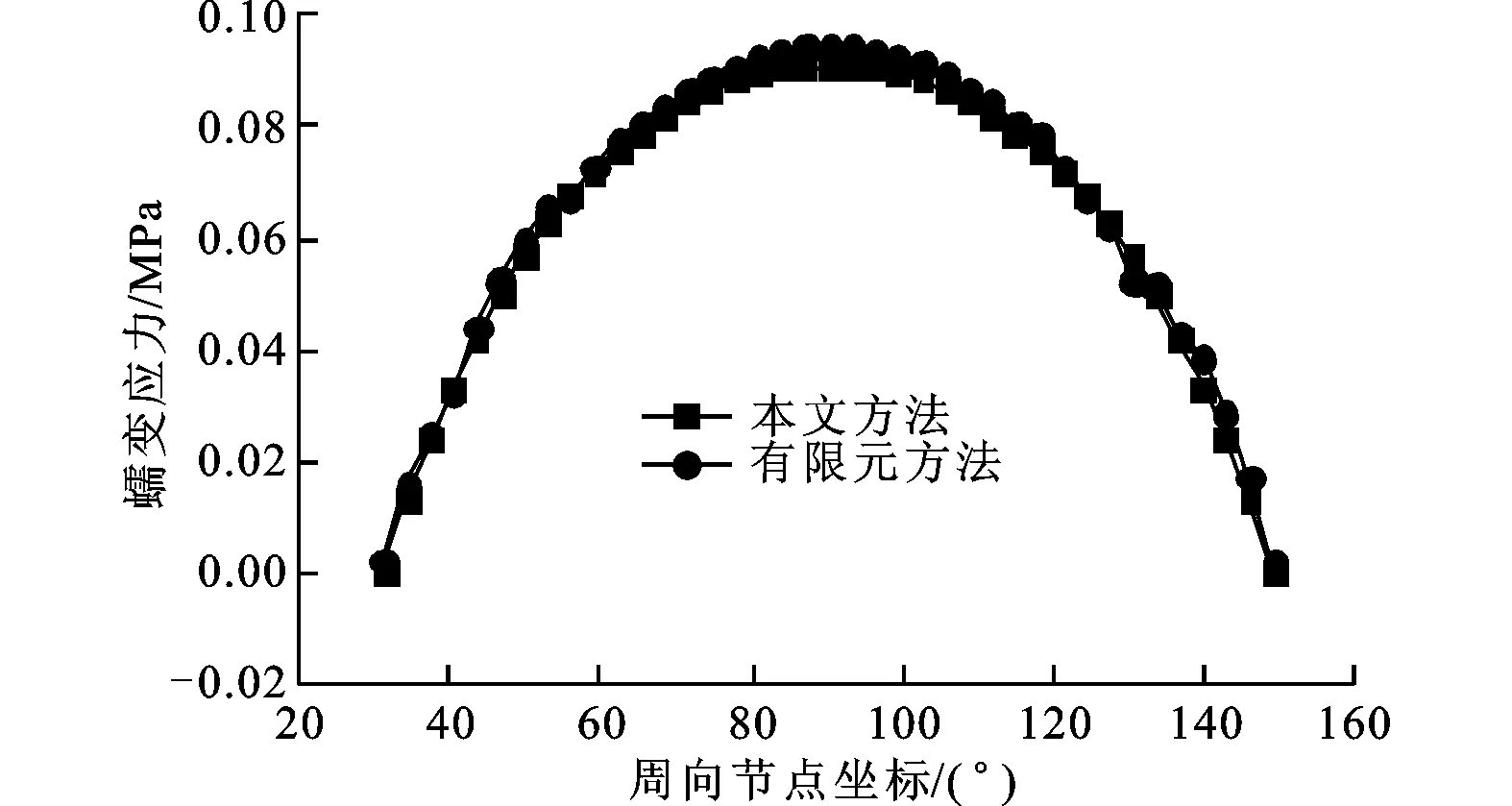
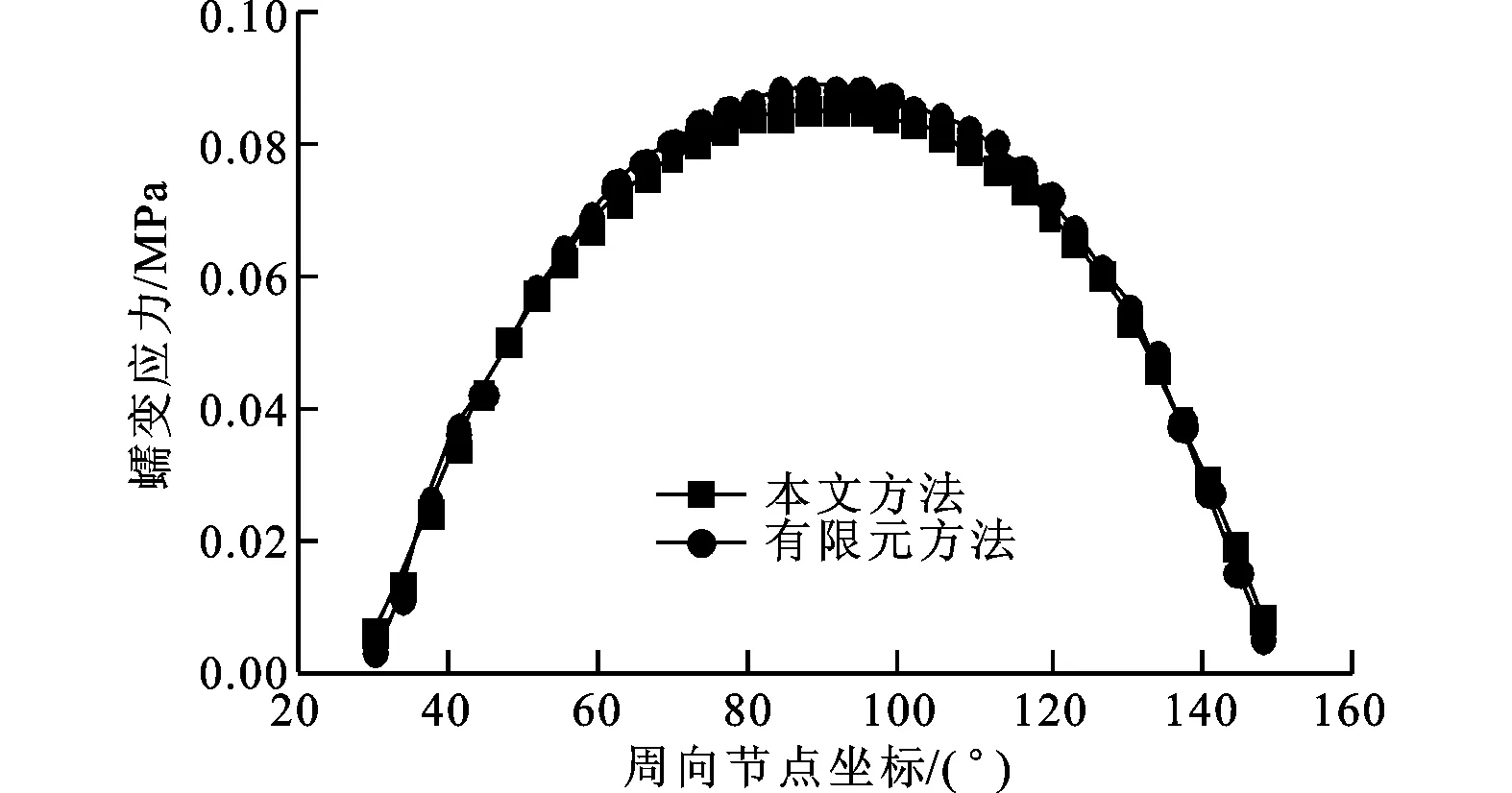
选定r为110、120 mm,θ为60°、90°分别对应的4个位置,采用本文方法与有限元方法对蠕变应力进行计算,结果对比如图9所示。

(a)r=110 mm

(b)r=120 mm

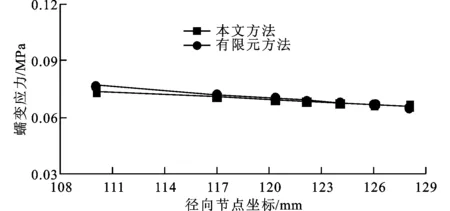
(c)θ=60°

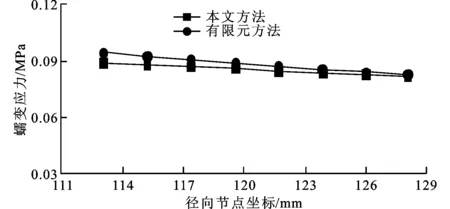
(d)θ=90°图9 本文方法与有限元方法计算的蠕变应力对比

由图9a和9b可知,本文方法与有限元方法计算的周向蠕变应力基本相同;由图9c和9d可知,本文方法与有限元方法计算的径向蠕变应力吻合较好。有限元方法较本文方法计算的结果略大,随着半径的增加,本文方法与有限元方法计算结果的误差逐渐减小。本文方法与有限元方法计算结果的最大误差在r=110 mm、θ=90°的位置,在此位置本文方法求得的蠕变应力为0.090 88 MPa,有限元方法求得的蠕变应力为0.094 43 MPa,二者的相对误差仅为3.9%,表明本文方法能够满足工程的实际需求。

5 结 论

(1)本文推导出了非均匀载荷下厚壁圆筒的稳态蠕变应力计算公式,计算了油膜轴承衬套在承受油膜压力时的蠕变应力;提出了一种新的多维蠕变应力求解方法,可以为多维蠕变应力解析求解提供理论依据。

(2)根据蠕变试验数据得到了诺顿稳态蠕变本构方程,并利用所得参数模拟了衬套的蠕变应力。本文方法的计算结果与模拟结果吻合,证实了本文方法的精确性,精度符合工程实际需求。

(3)得到了不同外内径比K下厚壁圆筒的蠕变应力及其分布,证实最大蠕变应力发生在厚壁圆筒内边界最大受力处,厚壁圆筒的最大蠕变应力随着壁厚的增加呈现出先增大后减小的规律,且当K=1.58时蠕变应力最大。这一结论可望为工程中厚壁圆筒的结构设计提供理论参考。

[1] LIANG Yaping, WANG Huizhen, REN Xingmin. Analytical solution for spatially axisymmetric problem of thick-walled cylinder subjected to different linearly varying pressures along the axis and uniform pressures at two ends [J]. Science in China: Series G Physics, Mechanics and Astronomy, 2008, 51(1): 98-104.

[2] ALTENBACH H, GORASH Y, NAUMENKO K. Steady-state creep of a pressurized thick cylinder in both the linear and the power law ranges [J]. Acta Mechanica, 2008, 195(1/2/3/4): 263-274.

[3] NAUMENKO K, ALTENBACH H, GORASH Y. Creep analysis with a stress range dependent constitutive model [J]. Archive of Applied Mechanics, 2009, 79(6/7): 619-630.

[4] BOYLE J T. The creep behavior of simple structures with a stress range-dependent constitutive model [J]. Archive of Applied Mechanics, 2012, 82(4): 495-514.

[5] WU Qingliang, LÜ Aizhong, GAO Yongtao, et al. Stress analytical solution for plane problem of a double-layered thick-walled cylinder subjected to a type of non-uniform distributed pressure [J]. Journal of Central South University, 2014, 21(5): 2074-2082.

[6] 吴庆良, 吕爱钟. 一类非均布荷载作用下厚壁圆筒平面问题的应力解析解 [J]. 工程力学, 2011, 28(6): 6-10, 18. WU Qingliang, LÜ Aizhong. Stress analytical solution for plane problem of a thick-walled cylinder subjected to a type of non-uniform distributed pressures [J]. Engineering Mechanics, 2011, 28(6): 6-10, 18.

[7] 郑俊德, 张艳秋, 王文军, 等. 非均匀载荷下套管强度的计算 [J]. 石油学报, 1998, 19(1): 119-123. ZHENG Junde, ZHANG Yanqiu, WANG Wenjun, et al. Calculation of casing strength under nonuniform loading [J]. Acta Petrolei Sinica, 1998, 19(1): 119-123.

[8] 穆霞英. 蠕变力学 [M]. 西安: 西安交通大学出版社, 1989: 60-83.

[9] 徐芝纶. 弹性力学 [M]. 北京: 高等教育出版社, 2006: 55-63.

[10]平修二. 金属材料的高温强度理论设计 [M]. 郭廷玮,李安定, 徐介平, 译. 北京: 科学出版社, 1983: 259-265.

[11]机械设计手册编委会. 机械设计手册: 第5卷 [M]. 3版. 北京: 机械工业出版社, 2004: 31-33.

[12]SIMMONS T E, CONTARINI A, GIANNI N. 油膜轴承变形和压力分析 [J]. 钢铁, 2009, 44(3): 93-96. SIMMONS T E, CONTARINI A, GIANNI N, et al. Deflection and pressure analysis of oil film bearings [J]. Iron and Steel, 2009, 44(3): 93-96.

[13]王建梅, 薛亚文, 马立新, 等. 蠕变对巴氏合金ZChSnSb11-6力学性能和显微组织的影响 [J]. 中国有色金属学报, 2014, 24(10): 2513-2518. WANG Jianmei, XUE Yawen, MA Lixin, et al. Influence of creep on mechanical properties and microstructures of Babbitt alloy ZChSnSb11-6 [J]. The Chinese Journal of Nonferrous Metals, 2014, 24(10): 2513-2518.

[14]GLADIUS L, SHAW K M. Creep constitutive model and component lifetime estimation: the case of niobium-modified 9Cr-1Mo steel weldments [J]. Journal of Materials Engineering and Performance, 2011, 20(7): 1310-1314.

[15]中国钢铁工业协会. GB/T 2039—2012 金属材料单轴拉伸蠕变试验方法 [S]. 北京: 中国标准出版社, 2012.

(编辑 葛赵青)

(太原科技大学教育部重型机械工程技术研究中心,030024,太原)

根据多维应力下稳态蠕变的基础理论,采用应力函数法推导出一类外边界固定、内边界受非均匀载荷的厚壁圆筒稳态蠕变应力计算公式;分析了不同外内径比K下厚壁圆筒的蠕变应力和应力分布情况,证实最大蠕变应力发生在厚壁圆筒内边界最大受力处,厚壁圆筒的最大蠕变应力随着壁厚的增加呈现出先增加后减小的规律,且当K=1.58时蠕变应力最大。应用所得计算公式,针对工程中油膜轴承衬套因承受油膜压力而发生的蠕变问题进行了蠕变应力解析求解。通过蠕变拉伸试验,得到了衬套内壁材料的诺顿稳态蠕变本构方程,并根据蠕变系数,利用有限元分析软件ANSYS计算了衬套的蠕变应力。最后,比较了上述2种方法得到的蠕变应力,表明文中给出的计算方法与有限元方法所得结果吻合,验证了该解析算法的正确性,从而可以为厚壁圆筒的结构设计和多维蠕变应力解析求解提供理论依据。

厚壁圆筒;稳态蠕变应力;非均匀载荷;蠕变试验;诺顿本构方程;有限元;油膜轴承衬套

Steady-State Creep Stress Calculation of Thick-Walled Cylinder under Non-Uniform Load

WANG Jianmei,MIAO Kejun,XU Junliang,LI Pu

(Heavy Machinery Engineering Research Center of Ministry of Education, Taiyuan University of Science and Technology, Taiyuan 030024, China)

Based on the basic theory of steady-state creep under multi-dimensional stress state, a steady-state creep stress calculation formula of thick-walled cylinder with fixed outer boundary was derived by the stress-function method under non-uniform internal pressure. The creep stress and stress distribution of several kinds of thick-walled cylinder were analyzed, which showed that the maximal creep stress occurred in the area with the largest stress on the inner boundary of the thick-walled cylinders, increased first and then decreased with the wall thickness, and the largest creep stress was produced when the ratio of outer diameter to internal diameter is 1.58. According to the formula, the steady-state creep stress of oil-film bearing bushing subject to a non-uniform oil-film pressure was analyzed, and the creep process was simulated by using the finite element software in ANSYS, where the creep parameters were obtained based on creep tensile test. Calculation results of the above two methods were analyzed, and the results obtained by the proposed method were coincident well with those by finite element method. This research may provide a theoretical guidance for the structural design of thick-walled cylinders and the analytical calculation of multi-dimensional creep stress.

thick-walled cylinder; steady-state creep stress; non-uniform load; creep test; Norton constitutive equation; finite element method; oil-film bearing bushing

2015-01-14。 作者简介:王建梅(1972—),女,教授。 基金项目:国家自然科学基金资助项目(51205269);山西省自然科学基金资助项目(2012011018-2);山西省回国留学人员科研资助项目(2013-093)。

时间:2015-06-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20150617.0902.001.html

10.7652/xjtuxb201509002

TH123

A

0253-987X(2015)09-0008-06