伪DNA密码图像加密算法研究

毛彦斌,张选平,杨晓刚



伪DNA密码图像加密算法研究

毛彦斌,张选平,杨晓刚

随着计算机网络的快速发展,在日常生活中用网络进行数字图像传输已经变得非常普遍。然而,由于网络的开放性和自身协议中存在的某些缺陷,数字图像在网络上传输的安全问题已经成为人们研究的热点。在众多的数字图像安全保护中,图像加密是一种行之有效的方法。相对于文本数据,数字图像有数据量大、冗余度高、相关性强等特点。因此,传统的诸如DES、IDEA和AES等加密方法并不适合数字图像的加密[1-2]。近年来,学者们提出了很多关于图像加密的新算法。例如,基于混沌理论的图像加密方法[3-6]和基于DNA序列的图像加密方法[7]。基于混沌理论的图像加密算法主要分为像素位置置乱和像素值扰乱两个过程[8-10]。因简单置乱不能改变原始图像像素值的分布规律,所以不能有效抵抗统计攻击,而只进行扰乱,不进行像素位置置乱,则很难抵抗剪切攻击。所以,很多学者在加密过程中将两者结合起来使用,以达到更高的安全性。高维混沌系统由于具有密钥空间大、对初值敏感性高和混沌特性更加复杂等优点,因此被广泛应用于图像加密中。Wang等提出了一种基于高维混沌系统的图像加密算法[11],仿真实验表明,该算法密钥空间大、对密钥敏感、安全性高。随着NDA计算的研究和发展,DNA加密作为一个新的研究领域倍受学者们的青睐。Celland等提出了一种新的加密方法[12],用DNA运算代替了传统的二进制加密;Shyam等提出了一种新的基于DNA计算的加密算法[13],他们用自然的DNA序列对原始信息进行编码,然后进行异或操作,以此实现对文本的加密。以上加密都是基于DNA生物操作,对实验环境要求苛刻,实验设备昂贵,在一般实验室很难完成相应的实验。近年来,Kang提出一种伪DNA加密方法[14],主要利用生物分子学中心法则的基本思想来实现信息的加密,但此方法只能对文字进行加密,不能对图像进行加密。为了克服以上基于混沌映射和DNA序列加密的缺点,本文采取伪DNA密码思想与高维混沌映射相结合的方法对图像进行加密。

1 混沌系统与DNA相关知识

1.1 混沌序列

本文研究的图像加密算法中涉及到二维Logistic混沌映射、Chen混沌映射、PWLCM混沌映射3个混沌映射,下面分别介绍这3个混沌映射。

二维Logistic映射形式为

(1)

式中:x和y是状态变量,x、y∈(0,1);μ1、μ2和γ是控制参数,当μ1,μ2∈[0.89,0.9]、γ∈(0,1)时,系统处于混沌状态。

Chen混沌映射是一种三维的混沌映射,其映射

形式为

(2)

式中:x、y和z是状态变量;a、b和c是正实数。当a=35、b=3、c∈[20,28.4]时,混沌系统便进入混沌状态。

PWLCM混沌映射也是一种典型的混沌映射,其映射形式为

(3)

式中:μ∈[0,1];xn∈(0,1),n=0,1,2,…。当0≤μ<0.5时,系统进入混沌状态;当0.5≤μ≤1时,系统逐渐进入分岔期,直至收敛为一点。

1.2DNA序列运算规则

1.2.1 DNA编码 单链DNA序列由腺嘌呤A、鸟嘌呤G、胞嘧啶C和胸腺嘧啶T 4种碱基组成[15],其中A与T、C与G互补。算法中用A、C、G、T对四进制序列进行编码,共有24种编码组合。由于四进制0与3互补,1与2互补,所以在24种编码中,只有8种编码满足碱基互补配对原则。编码方法如表1所示。

表1 DNA序列的8种编码方法

1.2.2DNA序列的截取与延长操作 P1、P2均是一条完整的DNA序列,S1、S2和S3、S4分别是P1和P2的子序列,P3是将P1的子序列S2截取后得到的新DNA序列,P4是将P1的子序列S2连接到P2后得到的新DNA序列。

1.2.3DNA运算法则 随着DNA计算的发展,一些学者提出了DNA序列的生物和代数运算[16-17]。由于DNA序列有8种编码方法,因此在进行DNA异或运算时也有8种不同的结果。本文采用0-A,1-C,2-G,3-T的映射规则进行DNA编码,具体运算规则如表2所示。

表2 DNA序列异或运算法则

2 伪DNA密码图像加密算法

本文算法的加密流程如图1所示,加密过程为:利用外部密钥和图像尺寸共同产生混沌系统的初始条件和控制参数;利用二维Logistic混沌系统产生的伪随机数对原始图像进行置乱;将置乱图像转换为四进制序列,利用PWLCM混沌系统产生的伪随机数和四进制序列值对四进制序列进行DNA动态编码;利用Chen混沌系统产生一个与四进制序列等长的随机DNA序列,并与编码后的DNA序列进行异或运算及截取延长操作;选择一种DNA解码方式进行解码得到加密图像。

2.1 混沌系统初始条件的产生

混沌系统的初始条件是根据320位的外部密钥和图像尺寸共同产生的,初始条件包括初始状态变量x0、y0、p0、q0、r0、k0,控制参数包括μ1、μ2、μ3。外部密钥被分成8bit长的块Ki(i=0,1,…,40)。设置C=0,用C=Ki(C≫1)重复进行迭代操作,其中表示异或操作,x≫y表示x向右移y个比特位;然后,通过Ki=Ki(C≫3)对块Ki(i=0,1,…,40)进行修正。

计算混沌系统的初始条件,需产生9个数Qi(i=0,1,…,8),计算公式为

(4)

式中:W=n+248,n表示原始图像的尺寸。

混沌系统的初始条件为:x0=Q0,y0=Q1,μ1=0.89+0.01Q2,μ2=0.89+0.01Q3,p0=Q4,q0=Q5,r0=Q6,k0=Q7,μ3=0.5Q8。(x0,y0,μ1,μ2)为二维Logistic混沌映射的初始状态和控制参数;(p0,q0,r0)为Chen混沌系统的初始状态;(k0,μ3)为PWLCM混沌映射的初始状态和参数。

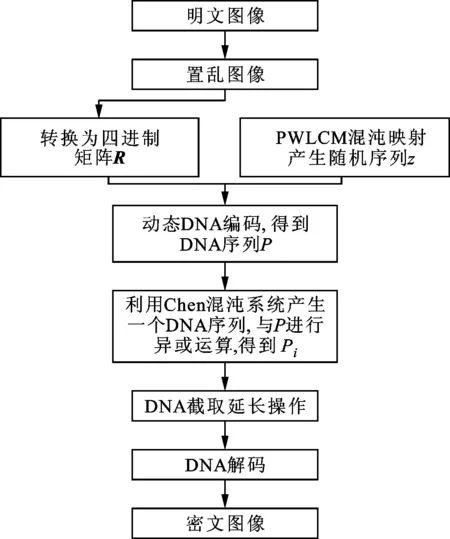
图1 伪DNA密码图像加密算法流程图

2.2 置乱算法

置乱算法的具体步骤如下:

步骤1 设置二维Logistic混沌映射初始状态(x0,y0),系统参数(μ1,μ2),从迭代的M步开始取(x0,x1,…,xi)、(y0,y1,…,yi),i=0,1,…,mn-1;

步骤2 根据zi=αxi+(1-α)yi产生新的伪随机序列(z0,z1,…,zi),i=0,1,…,mn-1,参数α∈(0,1);

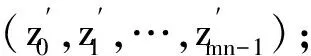
步骤5 将原始图像矩阵I转换为一维数组Ii,i=0,1,…,mn-1,而xi又对应位置wi,将原始图像一维数组I(i)用对应的I(wi)来替换得到置乱后的一维数组I′。

2.3 DNA动态编码

DNA动态编码的具体步骤如下:

步骤1 设置PWLCM混沌映射的初始状态(K0,μ3),从迭代的第M步开始取(k0,k1,…,ki),i=0,1,…,4mn-1;

步骤2 将ki随机数按照Vi=mod(floor(ki×1015),M×N)进行计算得到整数序列Vi,其中mod()为取模函数,floor()为取下整函数;

步骤3 将置乱后的图像转换为四进制序列Ri,i=0,1,…,4mn-1;

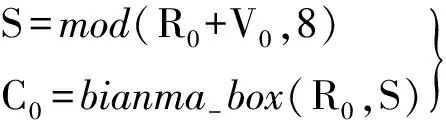
算法加密具体过程步骤如下:

步骤1 输入待加密的8位灰度图像I(m,n),(m,n)为原始图像I的行数和列数;

步骤2 设置二维Logistic混沌映射的初始状态(x0,y0),系统参数(μ1,μ2),从迭代的第M步开始取(x0,x1,…,xi)和(y0,y1,…,yi),i=0,1,…,mn-1;

步骤3 根据式(7)产生新的伪随机序列(z0,z1,…,zi),i=0,1,…,mn-1;

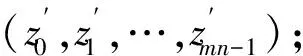
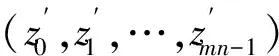
步骤6 将原始图像矩阵I转换为一维数组Ii,而xi对应位置wi,故可以将原始图像一维数组I(i)用对应的I(wi)来替代,得到置乱后的一维数组I′;

步骤7 设置PWLCM混沌映射的初始状态(k0,μ3),从迭代的第M步开始取(k0,k1,…,ki),i=0,1,…,4mn-1;

步骤8 将ki随机数进行计算得到整数序列Vi;

步骤9 将置乱后的图像转换为四进制序列Ri,i=0,1,…,4mn-1;

步骤10 根据四进制序列第一个值R0和整数V0计算S值,依据S值选择相应的编码方式对四进制序列第一个值进行编码得到C0;

步骤11 对四进制序列其他值进行DNA编码,得到动态编码后的DNA序列G;

步骤12 利用三维Chen混沌映射分别以初值(p0,q0,r0),从迭代的第L步开始取(pi,qi,ri)序列(i=0,1,…,(4mn-1)/3),产生一维随机序列fi(i=0,1,…,4mn-1),利用fi产生一个DNA序列T,将T与G进行异或运算得到G′

(5)

步骤13 选择一种解码方式对G′进行DNA解码得到四进制序列R′;

步骤14 根据R′值大小进行截取延长操作,并将截取延长后的四进制序列转换为十进制矩阵,得到最终加密图像。

3 实验结果与分析比较

3.1 实验结果

为了测试本文算法的性能,我们选取6个灰度级为256,大小分别为128×128、256×256、512×512、102 4×102 4的样本图像,实验用图如图2所示。

在Matlab2012环境下,对512×512的莉娜灰度图像进行加解密实验。加密和解密图像如图3所示。

(a)原始图像 (b)密文图像 (c)解密图像图3 加密和解密图像

3.2 置乱度定量分析

本文在对加密图像置乱度性能参数进行分析时,采取不动点比、灰度变化平均值、信息熵以及局部信息熵等方法来检验算法的置乱效果,下面分别介绍4种置乱度评价参数。

(1)设P=(pij)M×N表示大小为M×N的原始图像,C=(cij)M×N表示大小为M×N的加密图像,其中pij和cij是图像像素在位置(i,j)上的像素值。

若图像P中不动点占所有像素点的百分比用B(P,C)表示,则不动点比表示式为

(6)

(2)设P=(pij)M×N和C=(cij)M×N分别表示大小为M×N、灰度级为V的明文图像和密文图像,用G(P,C)表示两幅图像的灰度变化平均值,计算公式为

(7)

(3)信息熵是描述在一个给定的系统中不确定性或随机性的程度。计算公式为

(8)

式中:2N是总的样本数;mi∈m;p(mi)表示样本mi的概率分布。

(4)加密图像的局部随机性可以通过局部信息熵来测试[16]。(k,TB)局部信息熵定义为

(9)

式中:Si表示有TB个像素随机选择的互不重叠的图像块。文献[16]建议取k=30,TB=1 936。

对于加密理想的图像,不动点比在0.40%以内,灰度变化平均值差值在0.5以内,信息熵在7.996以上,局部信息熵在7.9以上。

下面以标准的512×512莉娜图像为测试图像,分别选取5组不同的密钥对测试图像进加密,得到5幅加密图像然后进行分析评价,表3给出了分析结果。

从表3可以看出,不动点比、灰度变化平均值、信息熵和局部信息熵4个置乱度评价参数均取得了比较理想的值。在5组数据中,每幅加密图像的不动点比都比较小,均没有超过0.4%;从明文图像与密文图像的差值变化情况来看,在不同密钥条件下,5幅密文图像与明文图像的灰度变化平均值变化非常均匀,灰度变化平均值在72.7～73.1之间,图像的最大灰度变化平均值与最小灰度变化平均值之差没有超过0.5。从5组数据中可以看出:加密图像和原始图像的灰度差是均匀变化的;5组密文信息熵均超过7.996,非常接近8的理想值。由此可见:密文图像的灰度值分布非常均匀;图像的局部信息熵均在7.9左右,因此本算法加密的密文图像有很好的局部随机性。综上所述,本算法所得加密图像置乱效果较好,安全性较高。

表3 置乱度评价参数

3.3 安全性分析

(a)莉娜 (b)莉娜1 (c)图4a和b的差值图

(d)莉娜加密图像(e)莉娜1加密图像(f)图4d和e的差值图图4 密文差值图

3.3.1 差分攻击分析 差分攻击的手段主要是将原图像做细微改变,然后用相同的密钥分别对原图像和修改后的图像进行加密,通过比较和统计两幅加密图像之间的差别,找出明文图像和密文图像之间的规律和联系,以此来破解算法。因此,一个好的加密算法应该能够有效地抵抗差分攻击。本文算法中,明文图像像素即使发生1bit的变化,所加密的图像也会与原始图像加密的密文图像截然不同。为了测试算法的明文敏感性,实验中将莉娜图像(75,480)坐标处的像素点设置为0,其余像素点不变,得到改变后的图像莉娜1如图4所示。然后,用相同的密钥对莉娜和莉娜1进行加密,得到密文图像C1和C2。

加密算法中明文的敏感性通常用像素变化率T和归一化平均变化强度U来计算。假设C1和C2仅是1 bit不同的明文图像加密得到的密文图像。c1(i,j)和c2(i,j)分别代表密文图像C1和C2在第i行、第j列的灰度值,则T和U的计算公式为

(10)

(11)

式中:abs()表示取绝对值。如果c1=c2,D(i,j)=0;否则,D(i,j)=1。理想的加密算法,像素变化率值大约是99.6%,归一化平均变化强度大约是33.46%。

实验中,随机选择原始图像的一个像素进行改变得到改变后的图像,然后用相同的密钥对原始图像和改变后的图像进行加密,并计算两个密文图像的像素变化率和归一化平均强度。对于图2中的样本,每个样本测试1 000次。表4分别给出了每个样本的T和U的最大值、最小值和平均值。从表6中可以看出,用本文提出的加密算法加密的图像的T值均在99.5%以上,U值均在33.2以上,非常接近理想值。也就是说,在相同的密钥条件下,即使原始图像改变1 bit,加密的图像与原始图像加密的图像也会截然不同。因此,本文算法有良好的雪崩效应,攻击者试图利用差分攻击的方法对算法或加密图像进行解密几乎是不可能的。

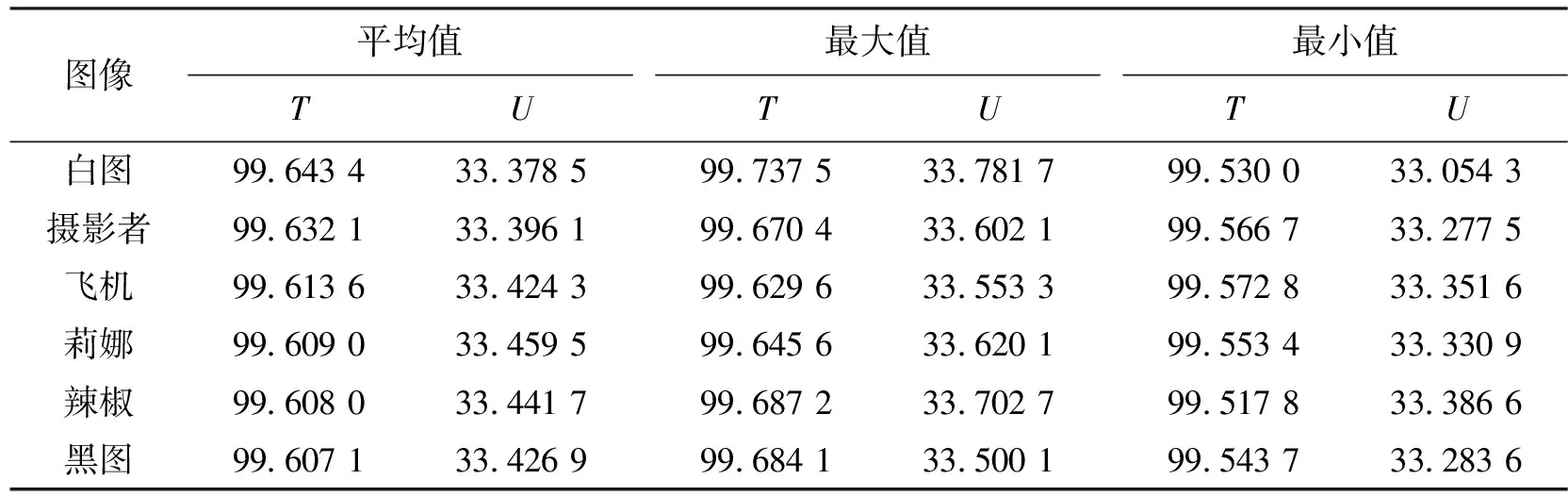
表4 明文敏感性分析表 单位:%

3.3.2 密钥空间分析 密钥空间的大小与能否抵抗穷举攻击有很大关系。因此,为了抵抗穷举攻击,一个好的图像加密算法应该有足够大的密钥空间,而且加密算法对密钥也要极其敏感。本文算法中,密钥空间为320 bit,其密钥空间是2320≈2.135 9×1096。根据目前计算机双精度浮点数的精度,我们取8 B、15 bit有效数字进行分析,设尝试一次破解所需时间的数量级为1 ms,则分析密钥空间穷举破解所需时间约为6.16×1085a。因此,本文算法密钥空间是足够大的,能够有效抵抗穷举攻击。

3.3.3 统计性分析 一个理想的加密算法要能够抵抗统计攻击。为了更加科学地验证和分析算法的加密效果及安全性,我们从直方图、卡方值、密文图像相邻像素之间的相关性3个方面来分析加解密图像。

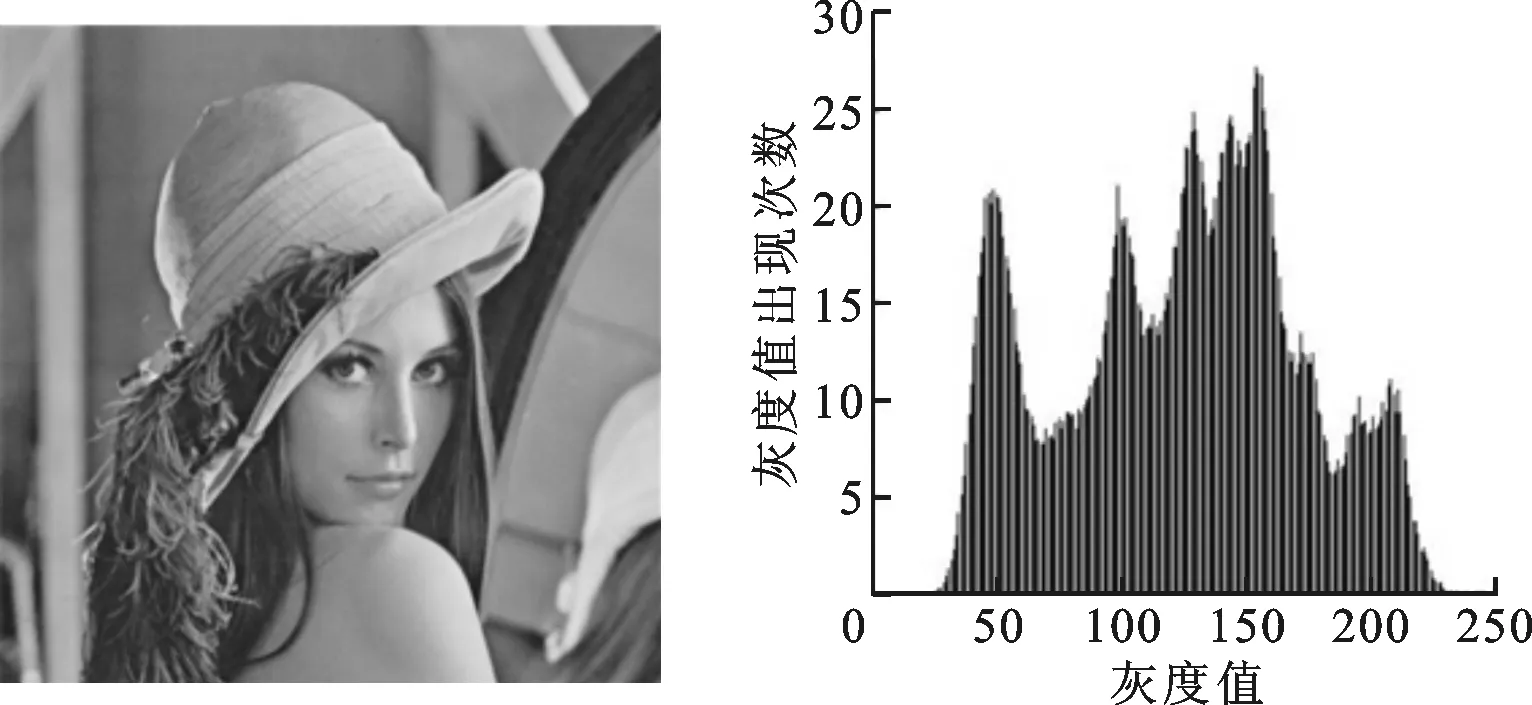
(a)原始图像 (b)原始图像直方图

(c)加密图像 (d)加密图像直方图图5 原始图像与加密图像直方图

图像直方图表征图像像素的分布情况,它是图像的重要统计特性之一。作为评价图像加密效果的标准之一,加密后的图像直方图变化越大,与原始图像差别越大,原始图像的视觉特征就越不明显。通常情况下,认为直方图越均衡,加密效果越好。图5显示了大小为512×512的莉娜原始图像和加密图像的直方图。从直方图来看,莉娜原始图像像素比较集中,(0,255)的两端像素分布比较少,而中间分布的较多,密文图像的灰度值分布相对比较均衡,基本接近理想的灰度值分布。因此,攻击者很难利用像素灰度值的统计特性得到有用的信息。图像像素值分布的均衡程度也可用卡方值χ2测试来进行分析,一个灰度级为256的图像的χ2计算公式为

(12)

式中:ni表示灰度为i的像素出现的频率;n/256是每个灰度级出现的期望频率。对于灰度级为256的图像,理想的加密图像卡方值应小于χ2(0.05,255)=293.5。

不同图像的明文图像和密文图像卡方值如表5所示,从表中可以看出,明文图像的卡方值非常大,而每个密文图像的卡方值均小于293.5,表明密文图像的直方图没有明显波峰,像素值分布比较均衡。原始图像像素间的相关性很高,为了抵抗统计攻击,必须降低加密图像的相关性。实验中,我们分别从原始图像和加密图像中随机选取在水平方向、垂直方向以及对角线方向上各1 000对像素点,然后计算各个方向的相关性,即

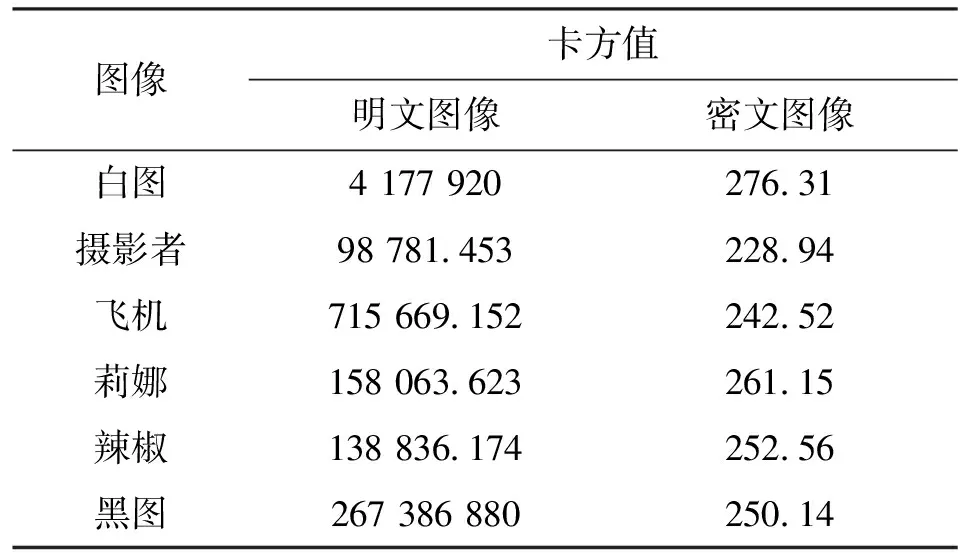
表5 卡方值分析表

(13)

原始图像和加密图像相邻像素的关联度如表8所示。一幅自然图像相关性应在0.9以上,接近1,效果理想的加密图像相关性应在0.01以下,接近0。

从表6可以看出,明文图像无论水平、垂直、对角线方向的两个相邻像素的相关性都接近于1,像白图和黑图两幅特殊单色图像,各方向相关性都等于1,说明原始图像相关性非常强。密文图像无论水平、垂直还是对角线方向,两个相邻像素之间的相关性都接近于0,表明原始图像经过加密以后,图像之间的相关性变得非常小,说明本文算法有很强的抵抗统计攻击的能力。

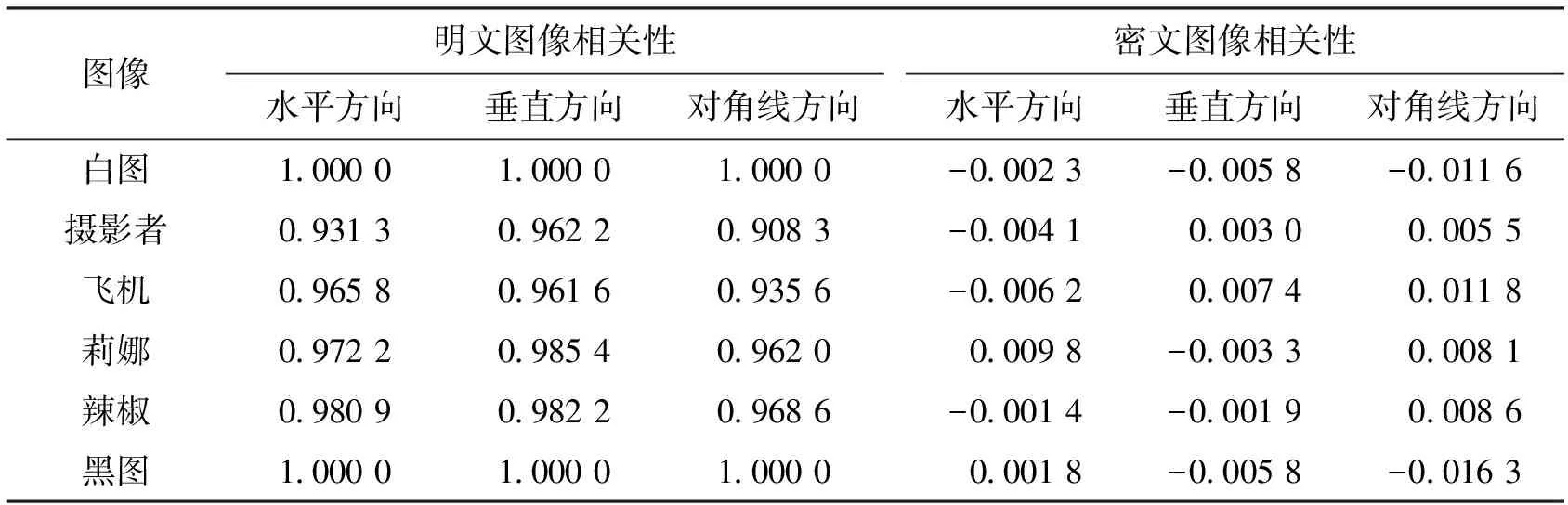
表6 相关性分析表

3.3.4 加密速度分析 一个好的加密算法不仅要有好的安全性,也要尽可能满足实时性的要求。仿真实验中,我们用Matlab2012在主频为3.10 GHz、内存为8 GB的win7操作系统下,对不同尺寸的灰度图像进行加密速度测试,每组测试进行100次实验,然后取加密时间的平均值,实验结果如表7所示。

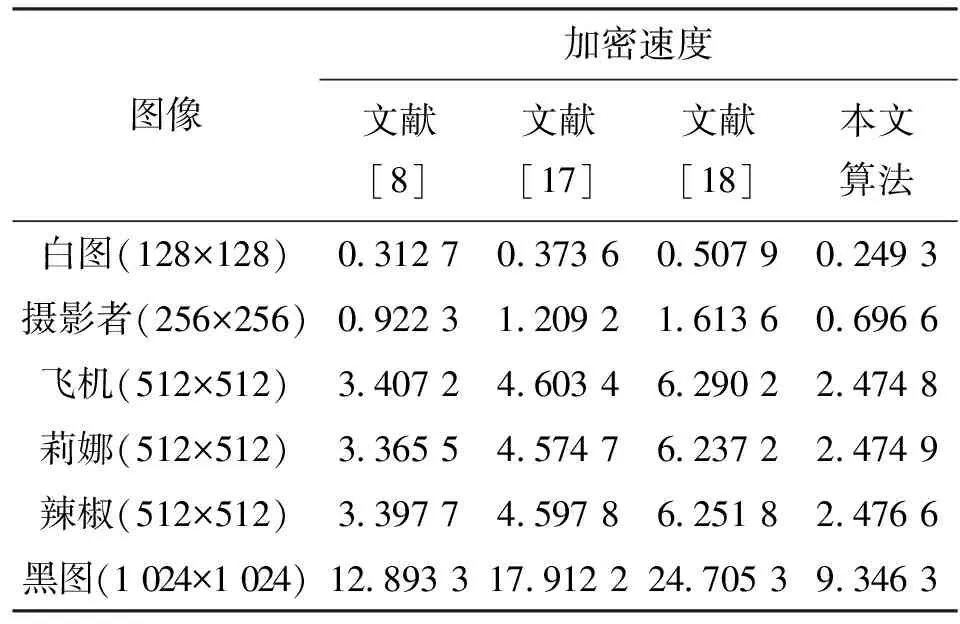
表7 加密速度分析表 单位:s

4 结 论

本文针对现有基于DNA序列的图像加密算法对实验条件要求苛刻、实验难以实现的不足,结合高维混沌系统和伪DNA密码思想的特点,提出了一种基于伪DNA密码思想的图像加密算法。将DNA加密的一些基本思想与混沌系统结合使用,增加了密文图像的安全性。针对静态DNA编码对原始图像进行编码不能有效抵抗差分攻击和统计攻击的不足,本文算法在编码过程中采用动态DNA编码方式,结合原始图像信息和混沌系统产生的随机数来选择编码规则;同时,根据编码后的密文数值对DNA序列进行延长截取操作,使密文图像安全性进一步提高。仿真实验结果表明,本算法具有较好的安全性和较快的加密速度,能够抵抗枚举攻击和统计攻击,适用于军事、医疗、司法等机密图像的保密存储和网络传输。

[1] LI S, CHEN G, CHENG A, et al. On the design of perceptual MPEG-Video encryption algorithms [J]. IEEE Trans Circuits Syst Video Technol, 2007, 17(2): 214-223.

[2] ZHANG G, LIU Q. A novel image encryption method based on total shuffling scheme [J]. Optics Communications, 2011, 284(12): 2775-2780.

[3] WANG Z, HUANG X, LI Y, et al. A new image encryption algorithm based on the fractional order hyperchaotic Lorenz system [J]. Chinese Physics: B, 2013, 22(1): 010504.

[4] ZHU C. A novel image encryption scheme based on improved hyper-chaotic sequences [J]. Optics Commu-nications, 2012, 285(1): 29-37.

[5] LIAN S G. A block cipher based on chaotic neural networks [J]. Neurocomputing, 2009, 72(4): 1296-1301.

[6] FU C, ZHU Z. Chaotic image encryption scheme based on circular bit shift method [C]∥The 9th International Conference for Young Computer Scientists. Piscataway, NJ, USA: IEEE, 2008: 3057-3061.

[7] WEI X, GUO L, ZHANG Q, et al. A novel color image encryption algorithm based on DNA sequence operation and hyper-chaotic system [J]. Journal of Systems and Software, 2012, 85(2): 290-299.

[8] ZHANG G, LIU Q. A novel image encryption method based on total shuffling scheme [J]. Optics Communications, 2011, 284(12): 2775-2780.

[9] LIAN S G, SUN J S, WANG Z Q. A block cipher based on a suitable use of the chaotic standard map [J]. Chaos, Solitons & Fractals, 2005, 26(1): 117-129.

[10]CELLAND C T, RISCE V, BANCROFT C. Hiding messages in DNA microdots [J]. Nature, 1999, 399(6736): 533-534.

[11]SHYAM M, KIRAN N, MAHESWARAN V. A novel encryption scheme based on DNA computing [J]. Nonlinear Dynamics, 2007, 23(1): 142-150.

[12]KANG N. A pseudo DNA cryptography method [EB/OL]. [2014-11-12]. http:∥arxiv.org/pdf/0903.2693v1.pdf.

[13]WATSON J D, CRICK F H. A structure for deoxyribose nuclei acid [J]. Nature, 1953, 171 (4356): 737-738.

[14]GABORITP, KING O D. Linear constructions for DNA codes theory Compute [J]. Nonlinear Dynamics, 2005, 334(1): 99-113.

[15]KING O D, GABORIT P. Binary templates for comma-free DNA codes [J]. Discrete Appl Math, 2007, 155(1): 831-839.

[16]WU Y, ZHOU Y, SAVERIADES G, et al. Local Shannon entropy measure with statistical tests for image randomness [J]. Information Sciences, 2013, 222(2): 323-342.

[17]XUE X, ZHANG Q, WEI X, et al. An image fusion encryption algorithm based on DNA sequence and multi-chaotic maps [J]. Journal of Computational and Theoretical Nanoscience, 2010, 7(2): 397-403.

[18]ZHANG Q, GUO L, WEI X P. A novel image fusion encryption algorithm based on DNA sequence operation and hyperchaotic system [J]. Optik, 2013, 124(18): 3596-3600.

(编辑 赵炜)

(西安交通大学电子信息与工程学院,710049,西安)

针对现有基于DNA序列的图像加密算法实验环境要求苛刻、难于实现的不足,根据DNA加密的基本思想,提出了一种伪DNA密码图像加密算法。该算法首先利用二维Logistic混沌序列对原始图像进行位置置乱,打乱像素之间的分布规律;然后,将置乱图像转换为四进制序列,根据事先定义的编码规则采用动态DNA编码方法将四进制序列转换为DNA序列;利用三维Chen混沌系统产生与四进制序列相同大小的DNA序列,将四进制编码的DNA序列和三维Chen混沌系统生成的DNA序列按照DNA异或规则进行异或运算;最后,进行截取延长操作并进行DNA解码重组得到加密图像。实验结果表明,该算法不仅容易实现,而且加密速度快、安全性高,可用于军事、医疗、司法等涉及个人和单位隐私的数字图像的保密存储和网络传输。

DNA序列;动态编码;混沌系统;图像加密

A Novel Image Encryption Algorithm Based on Pseudo DNA Coding

MAO Yanbin,ZHANG Xuanping,YANG Xiaogang

(School of Electronics and Information Engineering, Xi’an Jiaotong University, Xi’an 710049, China)

Aiming at the fact that existing image encryption algorithms based on DNA sequence have strict experimental conditions and are difficult to implement, an image encryption algorithm based on pseudo DNA coding is proposed combining DNA coding and chaotic system. Firstly, the original image is scrambled by using two-dimensional chaotic system. Secondly, the scrambled matrix is transformed into quarternary sequence which is then converted to DNA sequence by using dynamic DNA coding method. Thirdly, generating a random DNA sequence by three-dimensional chaotic system, with the same size as the quarternary sequence. Then, implementing DNA XOR operation on the quarternary DNA sequence and the DNA sequence generated by three-dimensional chaotic system, the encrypted image is obtained by decoding and reorganization. The simulation results and analysis show that the algorithm has not only good encryption effect but also fast encryption speed and high safety, which can be applied to the storage and network transmission of military, medical, judicial and other digital images.

DNA sequence; dynamic coding; chaos system; image encryption

2014-12-10。 作者简介:毛彦斌(1979—),男,硕士生;张选平(通信作者),男,副教授,硕士生导师。 基金项目:陕西省自然科学基金资助项目(2014JM8322)。

10.7652/xjtuxb201509016

TP391

A

0253-987X(2015)09-0091-08