地脚螺栓蠕变松弛对大型数控机床几何精度衰退的影响

刘海波,吴嘉锟,王永青



地脚螺栓蠕变松弛对大型数控机床几何精度衰退的影响

刘海波,吴嘉锟,王永青

数控机床床身是保障机床正常服役的关键基础件[1]。大型/重型数控机床的床身安装大都采用地脚螺栓分布预紧方式。预紧后的地脚螺栓蠕变松弛将直接影响螺栓预紧载荷大小、床身与地基间的连接刚度、床身应力分布等,导致床身几何尺寸发生变化,进而影响机床精度的保持状态。因此,研究数控机床服役过程中的地脚螺栓长期蠕变松弛行为,及其对床身预紧状态和几何精度的影响具有重要意义和工程价值。

国内外学者和研究机构针对金属材料结构的高温蠕变开展了大量的研究[2]。考虑到数控机床的实际工作环境,地脚螺栓的常温蠕变特征最为显著。Kassner等综述了常温/低温条件下的结晶材料的蠕变行为,讨论了蠕变塑性的基本机制[3]。Delhomme等基于黏弹性理论对内埋于混凝土的地脚螺栓进行了数值分析,预测了地脚螺栓预应力损失规律[4]。Fan等通过研究泥岩和螺栓瞬间粘合强度与螺栓蠕变速率、螺栓失效的关系,提出了螺栓在软质岩中的设计和应用准则[5]。Xu等根据螺栓拉拔蠕变实验,建立了螺栓拉拔刚度与蠕变损伤模型[6]。Kim研究了低压灌浆地脚螺栓蠕变松弛行为和载荷传递机制[7]。杨国庆等提出了一种螺栓被连接件轴向刚度高精度计算的半解析方法,实现了不同材料不同几何尺寸参数所对应被连接件刚度的精确计算[8]。Gurinsky分析了螺栓在黏性土壤中长期蠕变现象,并对螺栓变形进行了实验测试[9]。上述研究多面向单个螺栓的常温蠕变,而多个螺栓的常温蠕变行为及对连接性能的交互影响仍缺乏针对性研究。

大型数控机床床身地脚螺栓安装具有螺栓分布式、数量多、预紧交互影响显著等特征,床身在长期服役过程中的预紧状态及精度衰退规律复杂,因此有必要分析地脚螺栓蠕变松弛及其影响。

1 虑及螺栓蠕变的弹性交互作用模型

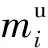
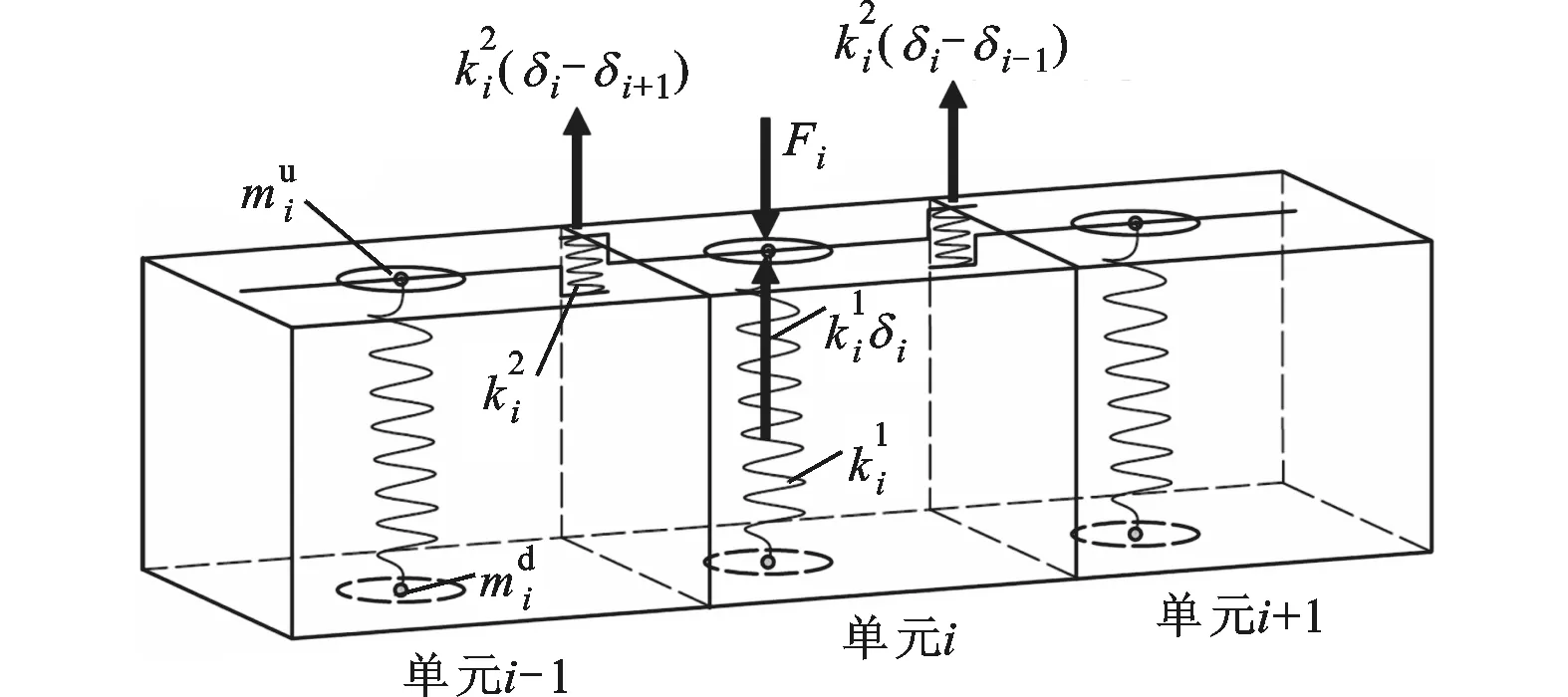
图1 螺栓孔的弹簧-节点模型

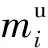
(1)

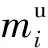
在常温环境下(T<0.3Tm,T为环境温度,Tm为螺栓熔点温度),基于时效硬化的幂律模型常用于描述金属常温蠕变行为[10],即

(2)

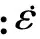
对式(2)进行蠕变时间积分,得到螺栓蠕变引起的轴向应变

(3)

在螺栓蠕变的影响下,螺栓预紧力

(4)

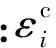
设螺栓组包含N个螺栓,根据式(1)可推导出预紧力弹性交互关系的通用模型

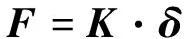
(5)

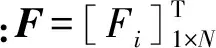
2 螺栓蠕变力的计算

2.1 计算模型

由式(4)和式(5)可知,螺栓实际预紧状态是由螺栓蠕变和蠕变螺栓间的弹性交互共同作用的结果,其中螺栓蠕变力是分析螺栓预紧状态变化的关键。螺栓蠕变力定义为由蠕变引起的螺栓轴向应变产生的力,即

(6)

式中:Fc为螺栓蠕变力;L为螺栓杆基本长度;δc为螺栓杆长度方向的蠕变量;ΔF为螺栓预紧力变化量;ΔFf为蠕变螺栓间弹性交互作用引起的力变化量。δc可直接根据蠕变前、后螺栓中杆长的变化计算得到。

由于在蠕变过程中螺栓变形为塑性的,所以E为变量,无法直接利用螺栓蠕变量δc计算螺栓蠕变力。根据式(6),螺栓蠕变力可通过计算ΔFf间接获取。

根据式(5),可推出

(7)

结合式(6)和式(7),得出N个螺栓蠕变力的计算式,即

(8)

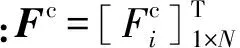
2.2 蠕变力的预测

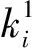
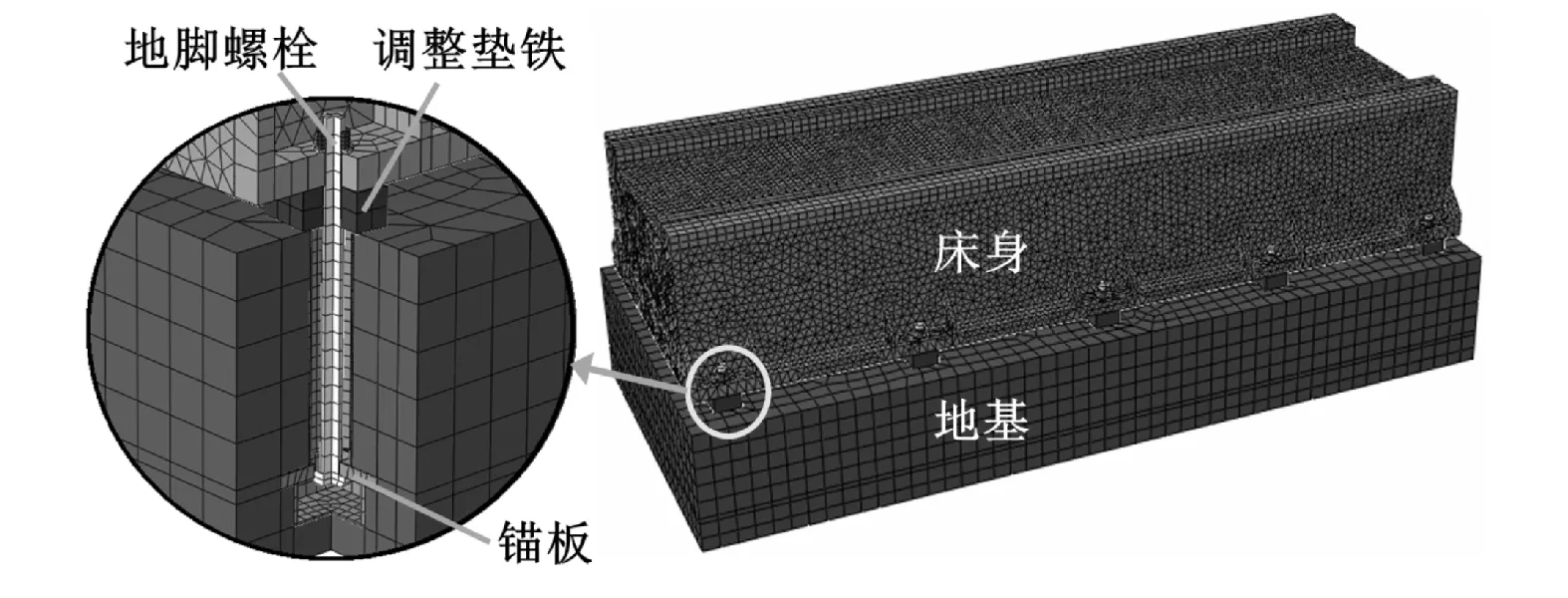
图2 地脚螺栓蠕变模拟模型

ui和li分别为标记在上和下导轨面的测点位置图3 地脚螺栓序列

所选的10个地脚螺栓被分成两排,对称分布于床身两侧,地脚螺栓定义序列如图3所示。采用中间向两边对称的预紧原则进行地脚螺栓组的预紧顺序规划,规划后的地脚螺栓预紧顺序为螺栓3—螺栓8—螺栓4—螺栓9—螺栓7—螺栓2—螺栓6—螺栓1—螺栓10—螺栓5,以获得优化后的初始预紧状态。

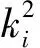
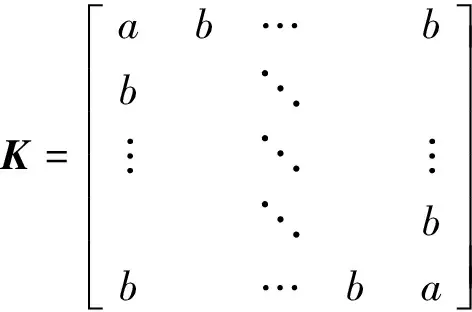
(9)

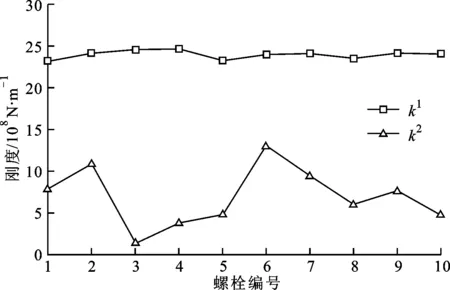
图4 螺栓孔单元刚度

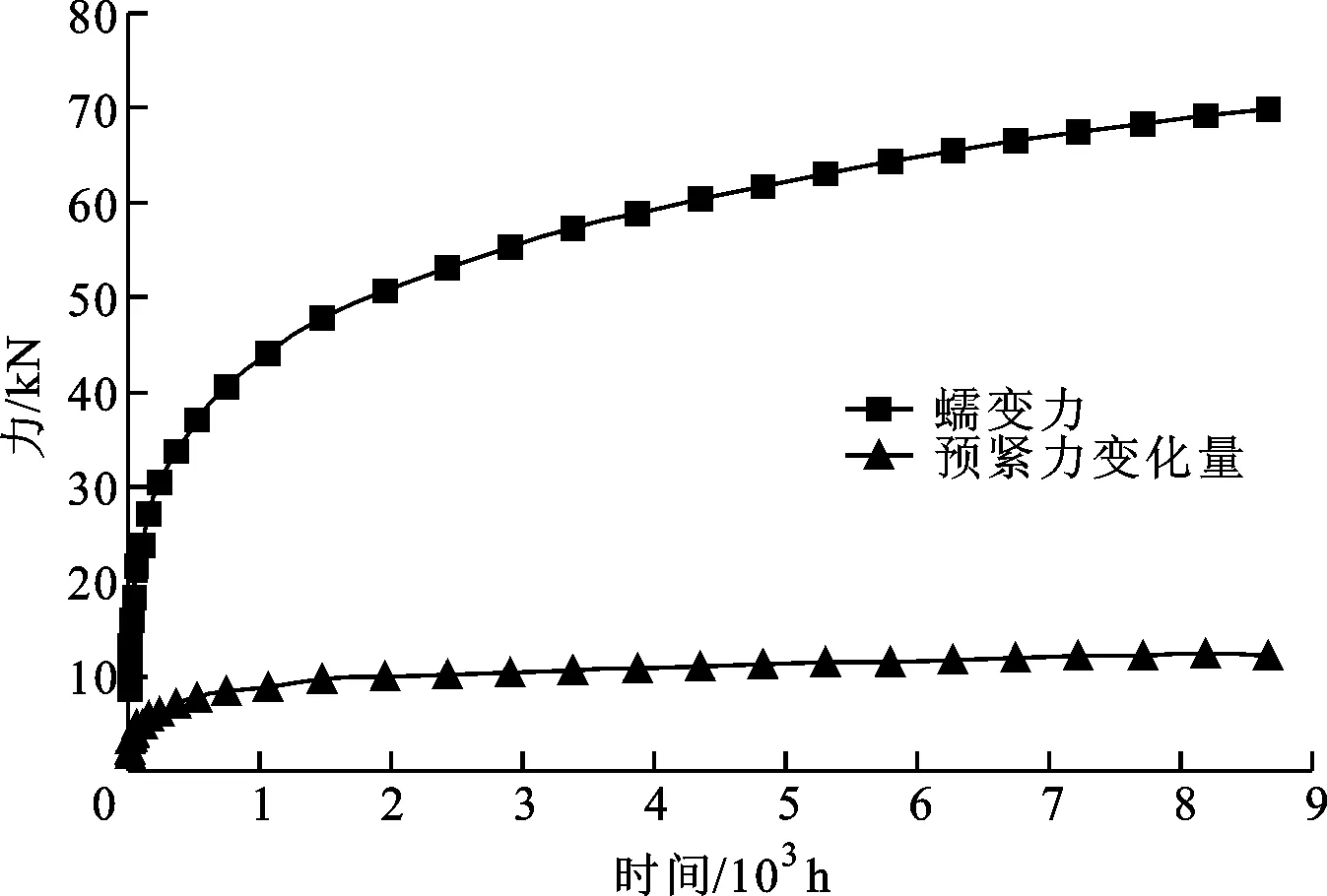
图5 3号地脚螺栓的蠕变力与预紧力变化量曲线

提取不同蠕变模拟时间节点的δc与ΔF,结合式(9)求得的K,并将其代入式(8)计算螺栓蠕变力。经9 000 h螺栓蠕变模拟,3号地脚螺栓的蠕变力及预紧力变化量如图5所示。由图可以看出,随着蠕变时间的推进,地脚螺栓蠕变力趋于稳定,而蠕变螺栓间的弹性交互作用对螺栓预紧力变化的影响逐渐增大。

3 机床几何精度衰退分析

为分析地脚螺栓长期蠕变松弛对床身导轨安装面的直线度、平行度等关键几何精度衰退的影响,在床身上、下2个导轨安装面的中线上依次均匀地取10个测点,得到2个测点序列Sui,i=1,2,…,10和Sli,i=1,2,…,10,ui和li分别为标记在上和下导轨面的测点位置,如图3所示。

由于螺栓蠕变及其弹性交互影响,使得螺栓残余预紧力松弛。按照规划顺序预紧后的螺栓初始预紧力和蠕变后的地脚螺栓残余预紧力对比曲线如图6所示。相比初始预紧状态,地脚螺栓预紧力的松弛比约为14.8%。不同蠕变时间节点的地脚螺栓残余预紧力标准偏差计算结果分布如图7所示。由图6和图7可知,随着螺栓蠕变松弛,螺栓组预紧力分布均匀性与残余预紧力变化速率有关。

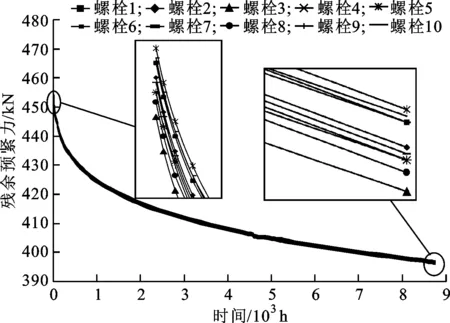
图6 地脚螺栓残余预紧力变化曲线

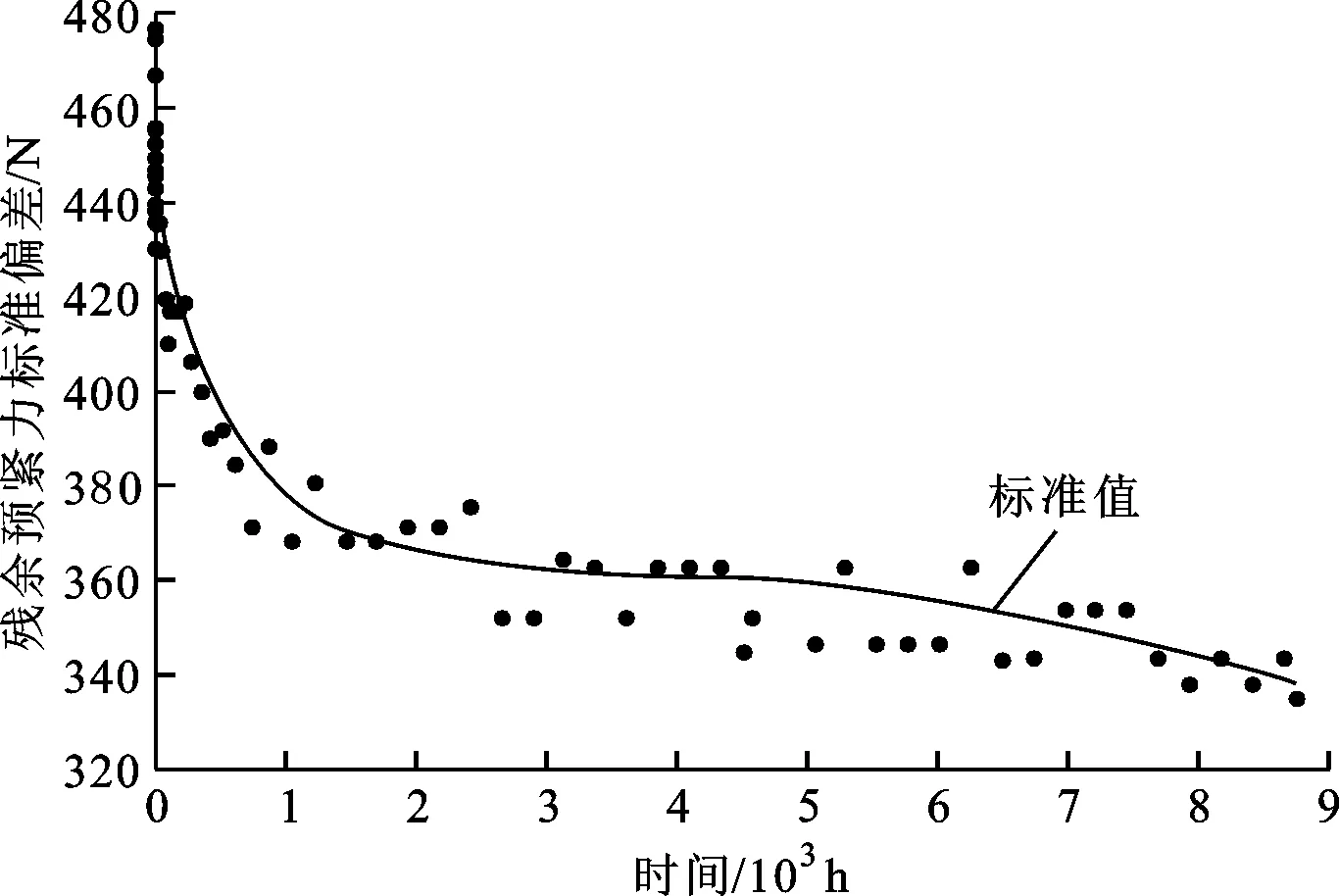
图7 蠕变螺栓的残余预紧力标准偏差

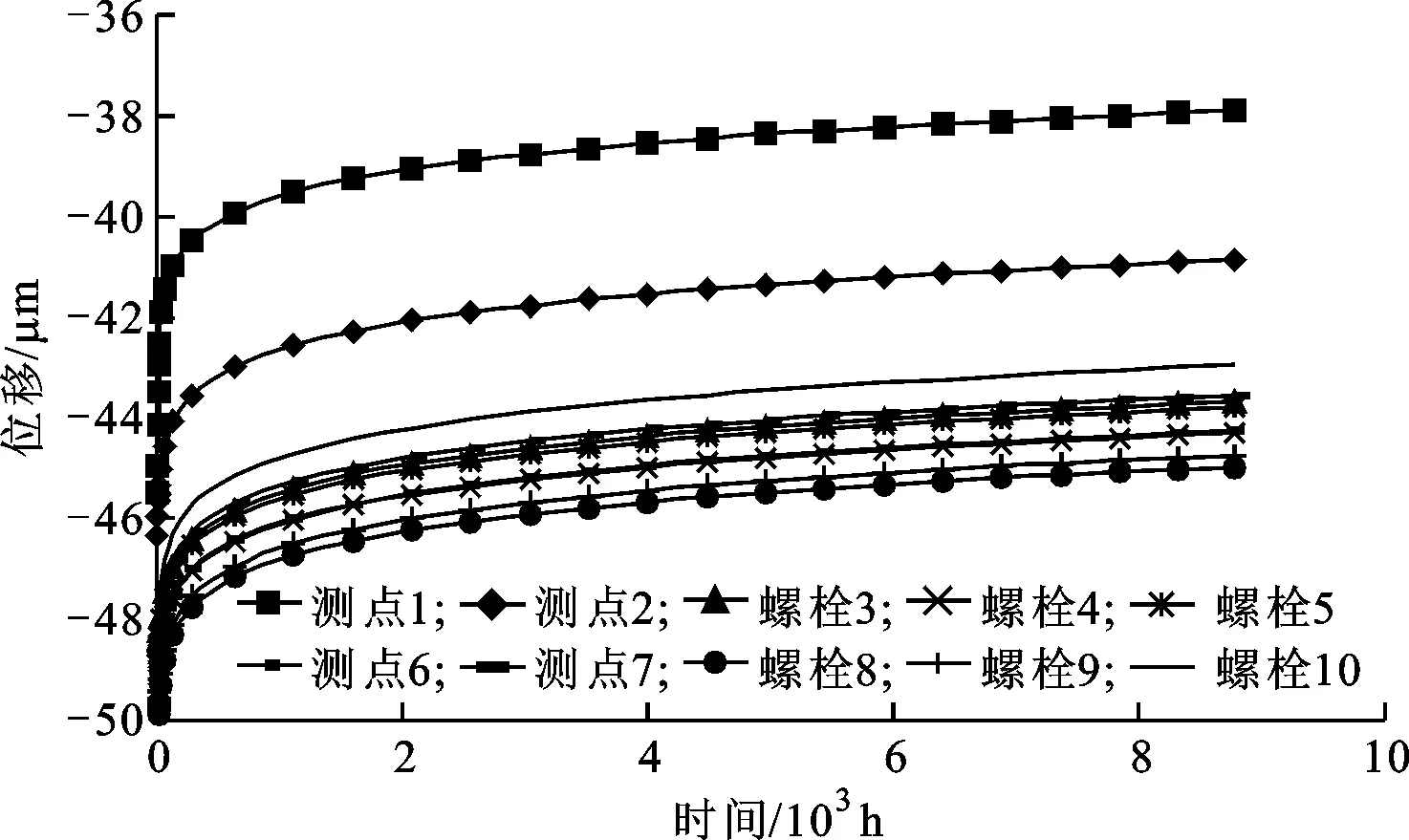
(a)序列Sui

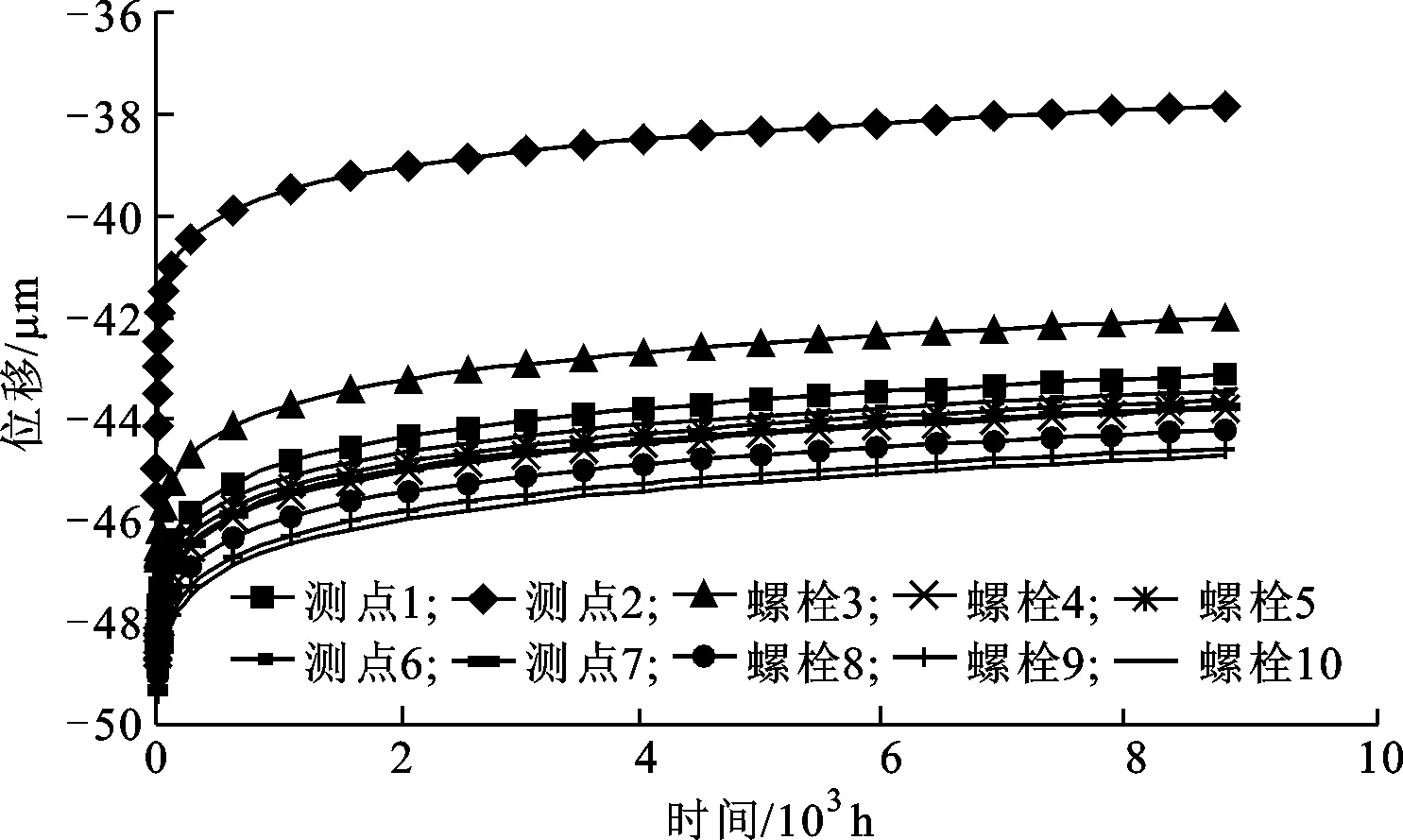
(b)序列Sli图8 测点蠕变位移曲线

床身导轨安装面上各测点由螺栓蠕变引起的位移曲线如图8所示。由图可以看出,各测点的最大蠕变位移约为10.4 μm,且蠕变位移与残余预紧力的变化趋势基本一致。根据各测点蠕变位移,按照标准ISO230-1计算出导轨面各直线度的最大相对衰减量为4.3 μm,两导轨平行度的相对衰减量为2.8 μm。

4 结 论

(1)通过对大型数控机床床身地脚螺栓预紧工艺分析,建立了虑及螺栓蠕变的弹性交互作用模型和螺栓蠕变力的计算模型,为大型数控机床地脚螺栓蠕变松弛行为的研究奠定了理论基础。

(2)开展了地脚螺栓长期、常温蠕变数值模拟,利用所建立的模型计算获得了机床服役一年的地脚螺栓蠕变力、残余预紧力和床身关键点蠕变位移的变化曲线。通过床身导轨安装面的直线度和平行度评估表明,地脚螺栓蠕变导致机床几何精度明显衰退,尤其对于精密/超精密数控机床,这种影响不可忽视。

(3)所建分析模型对优化机床床身等关键基础件的螺栓联接和研究大型数控机床几何精度的衰退规律具有重要意义和工程价值。

[1] 胡敏, 余常武, 张俊, 等. 数控机床基础大件精度保持性研究 [J]. 西安交通大学学报, 2014, 48(6): 65-73. HU Min, YU Changwu, ZHANG Jun, et al. Accuracy stability for large machine tool body [J]. Journal of Xi’an Jiaotong University, 2014, 48(6): 65-73.

[2] 涂善东, 轩福贞, 王卫泽. 高温蠕变与断裂评价的若干关键问题 [J]. 金属学报, 2009, 45(7): 781-787. TU Shandong, XUAN Fuzhen, WANG Weize. Some critical issues in creep and fracture assessment at high temperature [J]. Acta Metallurgica Sinica, 2009, 45(7): 781-787.

[3] KASSNER M E, SMITH K. Low temperature creep plasticity [J]. Journal of Materials Research and Technology, 2014, 3(3): 280-288.

[4] DELHOMME F, DEBICKI G. Numerical modelling of anchor bolts under pullout and relaxation tests [J]. Construction and Building Materials, 2010, 24(7): 1232-1238.

[5] FAN Q Y, LIU C L, YANG K Q, et al. Test study on creep character of anchor rod in argillaceous soft rock [J]. Advanced Materials Research, 2012, 396: 565-570.

[6] XU H, WANG F, CHENG X. Pullout creep properties of grouted soil anchors [J]. Journal of Central South University of Technology, 2007, 14: 474-477.

[7] KIM N K. Performance of tension and compression anchors in weathered soil [J]. ASCE Journal of Geotechnical and Geoenvironmental Engineering, 2003, 129(12): 1138-1150.

[8] 杨国庆, 王飞, 洪军, 等. 螺栓被连接件轴向刚度高精度计算的半解析方法 [J]. 西安交通大学学报, 2012, 46(9): 37-42. YANG Guoqing, WANG Fei, HONG Jun, et al. Semi-analytical method for accurate evaluation of axial stiffness of bolted member [J]. Journal of Xi’an Jiaotong University, 2012, 46(9): 37-42.

[9] GURINSKY M A. Long-term strength of prestressed ground anchors in creep-sensitive soils [J]. ASEC Geotechnical Special Publication, 2002, 116(1): 37-52.

[10]MAXIMOV J T, DUNCHEVA G V, ANCHEV A P. An approach to modeling time-dependent creep and residual stress relaxation around cold worked holes in aluminium alloys at room temperature [J]. Engineering Failure Analysis, 2014, 45: 1-14.

(编辑 苗凌)

(大连理工大学精密与特种加工教育部重点实验室,116024,辽宁大连)

针对大型数控机床地脚螺栓蠕变松弛的问题,建立了分布式螺栓预紧力和蠕变力的计算模型及螺栓顺序预紧和室温蠕变的模拟模型。计算模型中考虑了螺栓常温蠕变特征和螺栓孔单元间的弹性交互作用,量化分析时利用了模拟模型,以揭示蠕变松弛对机床几何精度衰退的影响规律。结合20 ℃环境温度下拉拔实验获得了8.8级T型地脚螺栓的3个蠕变系数,再经9 000 h蠕变模拟得到的地脚螺栓预紧力松弛比约为14.8%,床身导轨安装面直线度和平行度的相对衰退量分别为4.3 μm和2.8 μm。该结果表明,所建模型对大型数控机床基础件的螺栓预紧优化和几何精度保持能力的提升具有指导意义。

地脚螺栓;蠕变松弛;几何精度;精度衰退;大型数控机床

Impact of Anchor Bolts Creep Relaxation on Geometric Accuracy Decline of Large Computer Numerical Control Machine Tools

LIU Haibo,WU Jiakun,WANG Yongqing

(Key Laboratory for Precision and Non-Traditional Machining Technology of Ministry of Education, Dalian University of Technology, Dalian, Liaoning 116024, China)

Aiming at anchor bolt creep relaxation of large CNC machine tools, a calculation model for preload and creep force of the distributed bolts is established, where both bolts creep at room temperature and elastic interaction among bolt-hole units are taken into consideration. A simulation for anchor bolt sequential preload and creep is also conducted and utilized to reveal the influence of bolt creep relaxation on machine geometric accuracy decline quantitatively. Furthermore, three creep parameters of the 8.8 level T-type anchor bolt are estimated via the drawing experiments under 20 ℃ ambient temperature. After 9 000 hours creep simulation, the anchor bolt preload relaxation reaches 14.8%, and the relative accuracy declines of straightness and parallelism of bed linear guide mounting surfaces get 4.3 μm and 2.8 μm, respectively. The developed model can be used for the fundamental parts bolt preload optimization and the geometric accuracy retention capability enhancement of large CNC machine tools.

anchor bolt; creep relaxation; geometric accuracy; accuracy decline; large computer numerical control machine tool

2014-12-15。 作者简介:刘海波(1983—),男,讲师。 基金项目:国家科技重大专项资金资助项目(2014 ZX04014021);辽宁省科技创新重大专项资金资助项目(201301002-01)。

时间:2015-06-17

http:∥www.cnki.net/kcms/detail/61.1069.T.20150617.0902.007.html

10.7652/xjtuxb201509003

TH161

A

0253-987X(2015)09-0014-04