基于多尺度变换的直觉模糊推理图像融合算法
那 彦,刘 波
(西安电子科技大学 电子工程学院,陕西 西安 710071)
根据不同的处理阶段,图像融合分为像素级融合、特征级融合和决策级融合。由于本文中的方法均为像素级融合,故在此只讨论像素级融合方法。根据国内外图像融合的发展现状,近几年被广泛研究和应用的算法有:基于多分辨分析融合算法、基于人工智能融合算法等[1]。
在众多与智能技术相结合的融合算法中,基于模糊和直觉模糊的融合算法得到了广大学者的关注。但基于模糊推理的融合算法不能完全对于图像各像素点做详细描述,故针对以上不足,本文采用了多种多尺度变换结合直觉模糊推理融合算法,并与传统的模糊推理图像融合算法进行对比,以得到更好的融合结果。
本文算法是在变换域中引入直觉模糊推理系统,通过制定合理的融合规则确定直觉模糊推理系统。首先将待融合图像经过4 种多尺度变换,得到相应的高频分量和低频分量作为系统输入,再由输出的融合结果经过逆变换得到最终的融合结果。文中主要对Contourlet 变换、NSCT 变换、Waveletlet 变换和Shearlet变换进行验证,最终得到适用于医学图像融合中的Contourlet 变换[2]。
1 多尺度变换的基本理论
Fourier 分析反映了时间函数和频谱函数之间的关系,可以从中看出信号在整个时间范围内的频谱成分,但不具有时间局部化能力,所以提出了小波变换,其能提供较精确的时域和频域定位。小波变换善于处理点的奇异性问题和图像中的斑点部分,但不适用于线的奇异性问题。
而Contourlet 变换是一种多分辨、局域、方向的图像表示法,并且是将多尺度分析和多方向性分析分成两个相对独立的过程来实现[2-4]。其基本思想是使用双重滤波器组,首先采用拉普拉斯塔形分解(Laplacian Pyramid,LP)来完成多尺度分解以捕捉边缘奇异点,然后由方向滤波器组(Directional Filter Bank)将分步在同一个方向的奇异点合成为一个系数。
Contourlet 变换具有比Wavelet 变换分解出更多的方向子带,分解具有更多的方向信息。而且,Wavelet变换在每一尺度上只能分解出4 个方向子带,Contourlet变换在每一尺度上所能分解的方向自带是可以自由选择的,分解更具灵活性,可以根据图像的纹理特性选择合适的参数,从而能更有效的表示图像。
由于Contourlet 变换存在频谱混叠现象,因此为了消除此现象和增强其方向选择性和平移不变性,利用非下采样塔式分解和非下采样滤波器组构造出了非下采样Contourlet 变换(NSCT)。由于没有下采样的操作,NSCT 中的多分辨分解不是通过LP 分解实现的,而是直接通过满足Bozout 恒等式条件的移不变滤波器组来实现。
对于Contourlet 变换而言,Shearlet 变换的实现方法与Contourlet 变换是类似的,Contourlet 变换由拉普拉斯金字塔变换和一个方向滤波器构成;在Shearlet 变换中,Contourlet 变换的方向滤波器被换成了Shear 滤波器。相比于Contourlet 变换,对于Shearlet 变换来说,最突出的优点就是在Shear 滤波器下,没有方向数的约束。
2 直觉模糊推理系统
2.1 直觉模糊集
直觉模糊集的定义[5]如下:
设X 为一个给定的论域,则X 上的一个直觉模糊集A 为
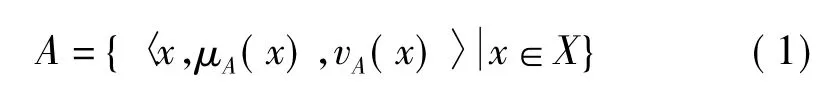
其中,μA(x)∶X→[0,1]和vA(x)∶X→[0,1]分别代表A的隶属度函数μA(x)和非隶属度函数vA(x),且对于A上所有x∈X,0≤μA(x)+vA(x)≤1 成立。
对于X 中的每个直觉模糊集,称πA(x)=1-μA(x)-vA(x)为A 中x 的直觉指数,它是x 对A 犹豫程度的一种测度。论域X 上的直觉模糊集A 由隶属度函数μA(x)和非隶属度函数vA(x)来表征,μA(x)的大小反映了x 对于直觉模糊子集A 的隶属程度,而vA(x)反映了x 对于直觉模糊子集A 的非隶属度程度,两者之和<1。
2.2 直觉模糊推理系统
直觉模糊推理本质上是一个从输入到输出的映射,并且该映射可以是复杂的非线性映射[6-9]。实现这一映射的主要机制是一组被称为规则的“if-then”语句,也称为“if-then”规则库,是整个推理系统的核心。
一个简单的“if-then”规则具有如下形式:if x is A,then y is B。其中,A 和B 分别用来表示论域X 和论域Y 上的直觉模糊集合,即A 和B 分别是论域上的直觉模糊集。规则的“if 部分”称为规则前件,规则的“then 部分”称为规则后件。
“if-then”规则表示了A 与B 之间的一种关系,称为直觉模糊蕴含关系[10],记为A→B,用模糊蕴含矩阵R 表示,本文使用Mamdani 型直觉模糊蕴含算子计算。
Mamdani 型直觉蕴含算子
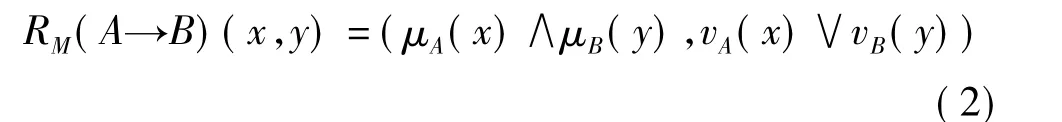
传统的模糊推理图像融合算法是设定一组“ifthen”推理规则并计算待融合图像像素点的隶属度,并将它们作为规则的激活因子,而待融合像素点依据隶属度的不同激活不同“if-then”规则进行融合从而得到融合图像。
本文的融合算法先确定“if-then”推理规则并建立推理系统,然后将待融合像素点直觉模糊化并输入推理系统中,得到融合图像对应像素点的推理结果。完整的直觉模糊推理系统推理过程,如图2 所示,其中直觉模糊化方法是单点直觉模糊化,解模糊方法采用重心法。
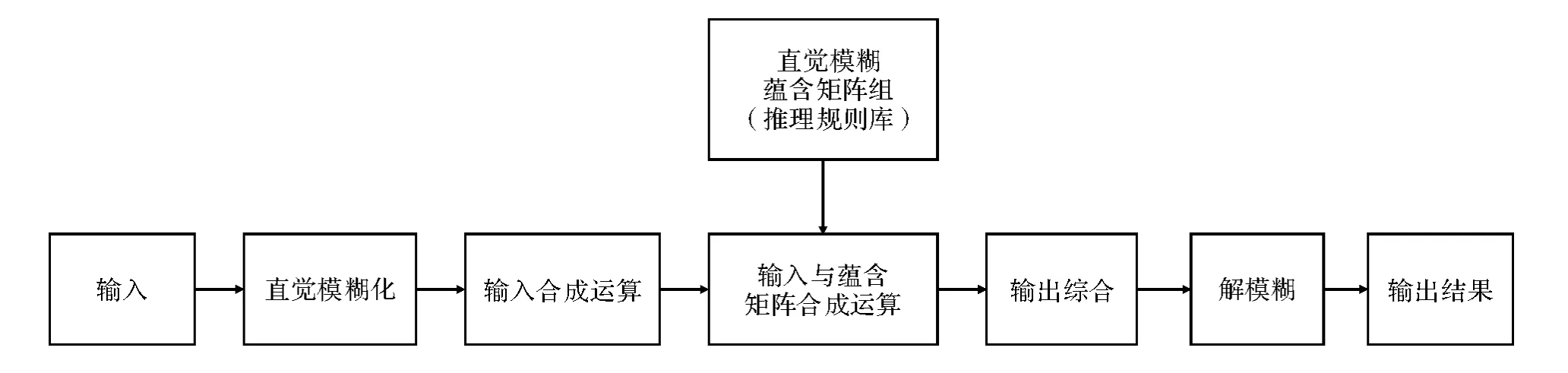
图1 直觉模糊推理系统
2.3 多尺度几何分析图像融合方案
根据上述不同融合规则,给出了基于多尺度变换的直觉模糊推理图像融合算法的流程框图,如图2 所示,采用CT 和MRI 图像作为输入的待融合图像,算法的具体流程为:
第1 步输入待融合图像,并进行预处理。
第2 步对待融合图像分别进行多尺度变换,分解为高频分量和低频分量。
第3 步对经过多尺度变换得到的低频分量和高频分量均采用用直觉模糊推理融合。
第4 步对融合后的低频、高频融合结果图像,运用相应的逆反变换得到最终的融合结果。
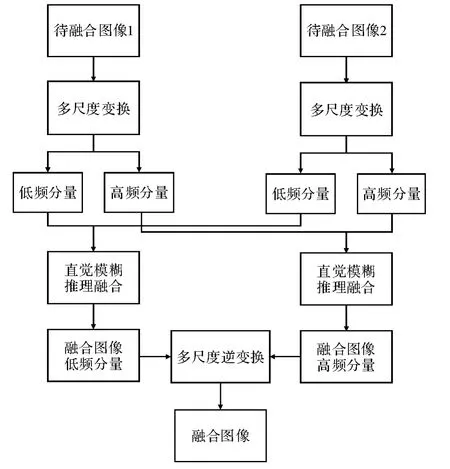
图2 基于多尺度变换的融合算法流程框图
4 图像融合实验及结果分析
采用CT 和MRI 医学图像进行融合实验,针对不同多尺度变换的融合结果如图3 所示。

图3 待融合CT 和MRI 图像
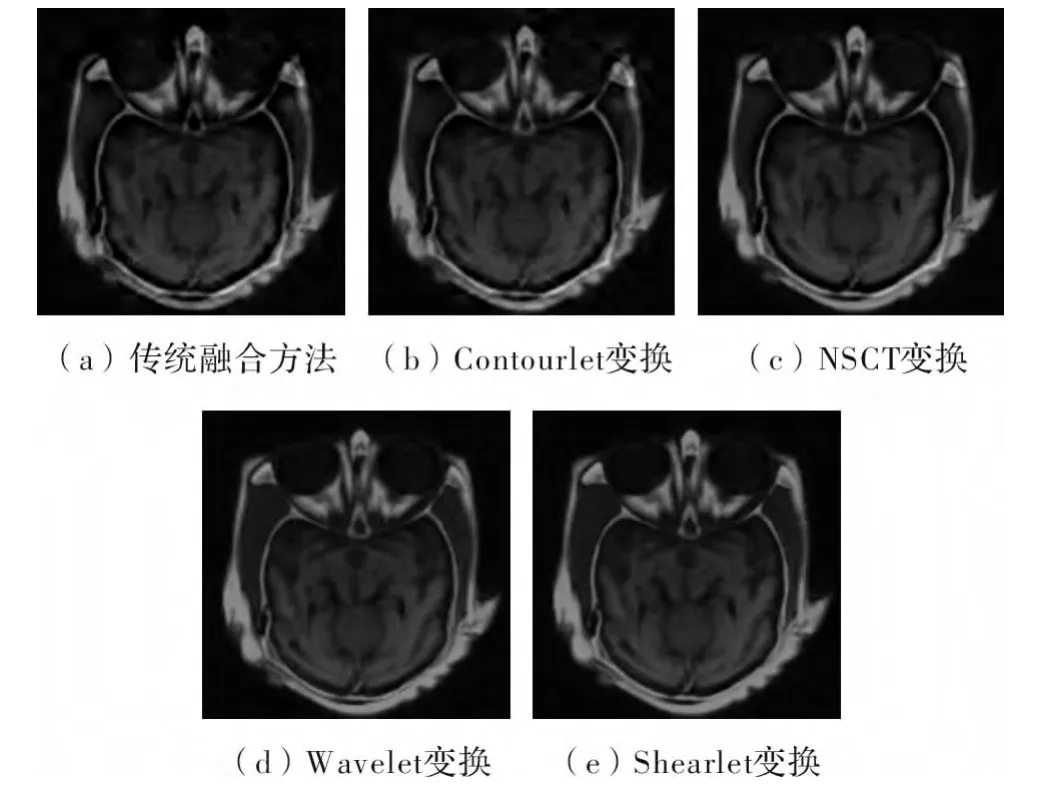
图4 融合结果图像
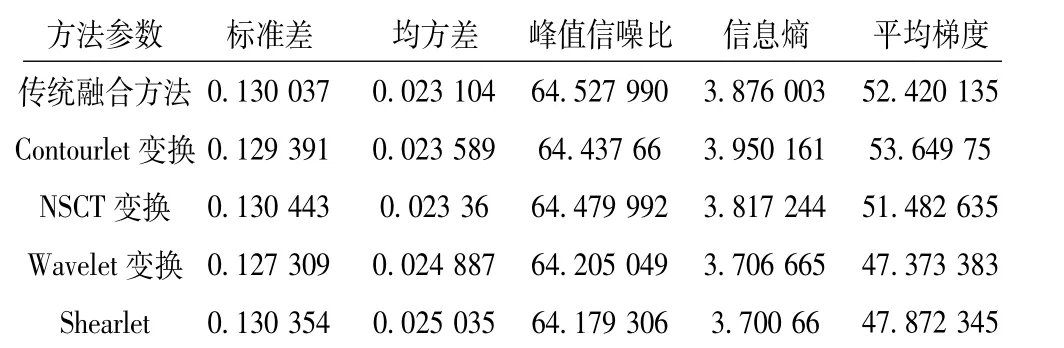
表1 融合结果参数对比
由上述参数评价表,可以看出传统的模糊推理融合算法的融合效果,明显低于直觉模糊推理融合算法。并且综合上述各种变换的优势以及评价参数,可以看出Contourlet 和NSCT 变换的融合结果要优于其它两种变换。由于NSCT 是为了消除Contourlet 变换的频谱混叠现象而提出的,它剔除了上采样和下采样,减少了采样在滤波器中的失真,获得了平移不变性,并且分解后的高低频分量的大小与原图相同,使得更多的细节得以保留。故在参数均方差和峰值信噪比上要优于Contourlet 变换。但是由于融合的最终结果是要使图像具有更清晰和更丰富的内容,而且信息熵和平均梯分别反映了图像包含信息的丰富程度和图像对微小细节反差表达的能力,即图像的清晰度。因此综合比较Contourlet 变换要略优于NSCT 变换。
5 结束语
本文研究了基于多尺度变换的直觉模糊推理医学图像融合方法,并与传统的模糊推理融合算法进行了对比。从视觉观测和评价参数上看,采用不同变换的直觉模糊推理融合算法,明显优于传统的模糊推理图像融合方法,并且在基于多尺度变换的直觉模糊推理图像融合方法中,Contourlet 变换要优于其它3 种变换。因此,基于多尺度变换的直觉模糊推理方法,能更好地实现对医学图像的融合处理。
[1] 那彦,焦李成.基于多分辨分析理论的图像融合方法[M].西安:西安电子科技大学出版社,2007.
[2] 焦李成,侯彪,王爽,等.图像多尺度几何分析理论与应用:后小波分析理论与应用[M].西安:西安电子科技大学出版社,2008.
[3] 沈洁.基于多分辨率分析的图像融合技术研究[D].扬州:扬州大学,2009.
[4] 邓艾.基于变换域的图像融合算法研究[D].武汉:武汉科技大学,2012.
[5] Teng Jionghua,Wang Suhuan,Zhang Jingzhou,et al.Fusion algorithm of medical image based on fuzzy logic[C].Fuzzy System and Knowledge Discovery,2010:546-550.
[6] 孙祺,那彦,刘波.直觉模糊推理融合算法研究[J].电子科技,2014,27(5):193-196.
[7] 刘天华.直觉模糊推理与决策的几种方法研究[D].山东:山东大学,2010.
[8] 吕大江,石志寒,雷英杰,等.基于Mamdani 型蕴含关系的直觉模糊推理仿真[J].计算机工程与设计,2010,31(11):2539-2542.
[9] 张震宇,陈鹰,邵永社.一种基于模糊集理论的图像融合方法[J].遥感信息,2008(4):7-10.
[10]Elpiniki I Papageorgiou,Dimitris K Iakovidis.Intuitionistic fuzzy cognitive maps[J].IEEE Transactions on Fuzzy Systems,2013,21(2):342-354.

