基于Shearlet 变换的多聚焦图像融合方法

邱万山，何建忠

(上海理工大学 光电信息与计算机工程学院，上海 200082)

图像融合是信息融合［1］的一个重要分支，也是图像理解和计算机视觉中的一项重要技术，其分为3 个层次，即像素级图像融合［2］、特征级图像融合及决策级图像融合，在像素级图像融合中，多聚焦图像融合直接在原始数据上进行融合，能保持尽可能多的现场数据，提供其他融合层次所不能提供的更丰富、可靠的信息，有利于对图像的进一步分析、处理与理解。

图像融合算法在早期是基于空域的，直接对源图像的像素灰度空间操作，实现简单，但效果欠佳。1983年，Burt P J 等人首先提出了金字塔变换［3］，开启了多尺度分解的序幕，之后基于小波变换［4］，Contourlet 变换［5］等的变换方法相继被提出。

1 Shearlet 变换

1.1 预备知识

Shearlet 变换［6－10］理论在2005 年提出，Glenn Easley等人将合成小波理论与传统的仿射系统理论相结合，提出了一种新的多尺度几何分析方法，通过对一个函数进行伸缩、平移、旋转生成一组基函数，使其和多分辨分析关联起来，能在不同尺度、不同方向对图像的细节信息进行有效描述。

Shearlet 变换解决了小波变换主要适用于表示具有各向同性的奇异性对象，而对于各向异性的奇异性对象，如图像中的边界及线状特征等并不能很好地表示的问题。

而与Contourlet 变换相比，Shearlet 变换变换最突出的优点就是在Shear 滤波器下，没有方向数的约束，并且Shear 滤波器也可通过一个矩形式的窗函数表示。

Shearlet 变换不仅具有多尺度、良好的时频局部特性，还具有多方向性，允许每个尺度上具有不同数目的方向分解，其基支撑区间能随尺度长宽比变化。其在图像处理方面的应用研究正在逐步扩展，研究主要集中在图像去噪［11］，边缘检测和图像分割方面，本文基于Shearlet 变换进行多聚焦图像融合。

1.2 连续Shearlet 变换

Shearlet 变换根据合成小波理论衍生而来。当维数n=2 时，具有合成膨胀的仿射系统定义为

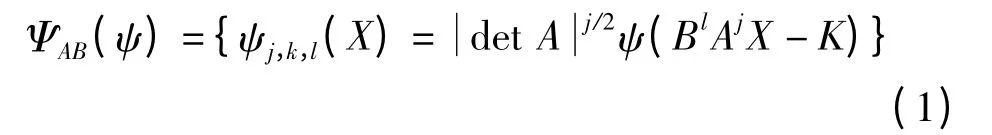
式中，j，l∈Z，k∈Z2，ψ∈L2(R2)，A 和B 为2×2 的可逆矩阵，若ΨAB(Ψ)满足Parseval 框架

则ΨAB(Ψ)的元素称为合成小波。其中，Aj与尺度变换相关联，Bl与面积不变的几何变换相关联，例如旋转和剪切。与小波相类似，合成小波可构造尺度、位置和方向变化的Parseval 框架，而Shearlet 是合成小波的一个特例。

1.3 离散Shearlet 变换

要将Shearlet 变换应用于图像融合，首先要进行离散化，这主要分为两个过程:首先在空间域进行多尺度分解，然后在伪极网格系统中利用窗口函数的平移获得不同方向的系数，令j(=1，2，…，M)表示图像的分解尺度，l(=1，2，…，N)为分解方向数，低频用j=0来表示，在文中简写为j0。

离散化的具体过程如下:

步骤1 应用拉普拉斯金字塔变换将图像分解成低频子带fj0和高频子带fj。

步骤2 将高频fj从直角坐标系转换到伪极网格坐标系，并在伪极网格上计算离散傅里叶变换，将fj转换至频域上的fj。

步骤3 在伪极网格上构建一个方向滤波器，再转换到直角坐标系，此时方向滤波器称为Shear 滤波器。

步骤4 对高频系数矩阵应用一个Shear 滤波器，通过滤波器的多方向分解，得到高频子带频域上的系数。

步骤5 对方向系数进行傅里叶逆变换，得到低频子带系数Cj0和一系列高频子带系数Cj，l。

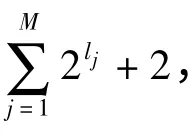
应用于图像融合中的具体步骤如下:首先对聚焦不同部分的两幅图像进行配准;之后对配准的图像分别进行Shearlet 分解，将图像分解成一个低频图像和若干个高频方向子带图像;然后分别对图像的低频图像和高频子带图像采用融合规则进行融合处理;最后进行Shearlet 逆变换，得到融合图像。

2 融合系数选择

图像融合不仅涉及图像变换所使用的变换方法，对变换后的系数进行恰当的处理也是决定图像融合效果的关键因素。考虑到人类视觉系统对细节信息比较敏感，而且图像模糊或清晰的特征不能由某个像素的灰度值来体现的特性，所以在选择系数时，需要考虑局部区域内的多个像素点。本文采用Shearlet 变换和区域特性相结合的图像融合方法。

图像的低频系数决定着图像的整体特征，本文取两幅源图像分解系数中区域能量高的系数作为融合图像的低频系数;对于高频系数，由于在多聚焦图像成像过程中，聚焦图像具有丰富的高频细节信息，而图像的区域能量，清晰度、方差等函数在某种程度上都能反映图像的高频细节信息，因而能够很好地体现多聚焦图像的聚焦特性，以及地区分多聚焦图像中的清晰区域和模糊区域。以往文献根据某个评价函数采用单一规则判定图像清晰区域和模糊区域，容易丢失图像的细节信息，而且噪声对图片的污染信息也会对这些融合度量函数产生影响，本文结合能量，清晰度、方差3 种函数，使用多判决法得到融合图像高频子带系数。

2.1 3 个聚焦评价函数

区域能量，区域清晰度、区域方差3 种函数的定义如下:

图像区域能量为

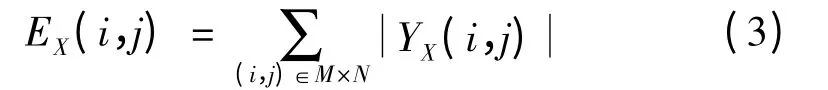
图像区域清晰度为

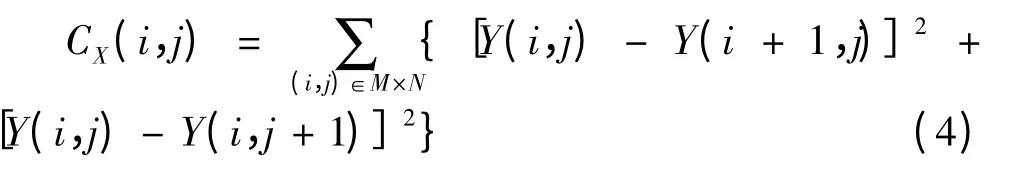
图像区域方差为

其中，X=A，B，A 和B 是两幅源图像;YX(i，j)是(i，j)点处的像素值;M，N 是邻域大小，本文选择邻域大小为是图像X 在邻域内的均值。

2.2 多判决选择法

对于高频系数，本文结合区域能量、区域清晰度以及区域方差这3 个能描述图像清晰度函数。

本文提出的融合规则如下:

首先分别对多聚焦图像A 和B 进行Shearlet 分解，对图像的高频子带系数对应计算其邻域的清晰比、能量比和方差比，计算公式分别为

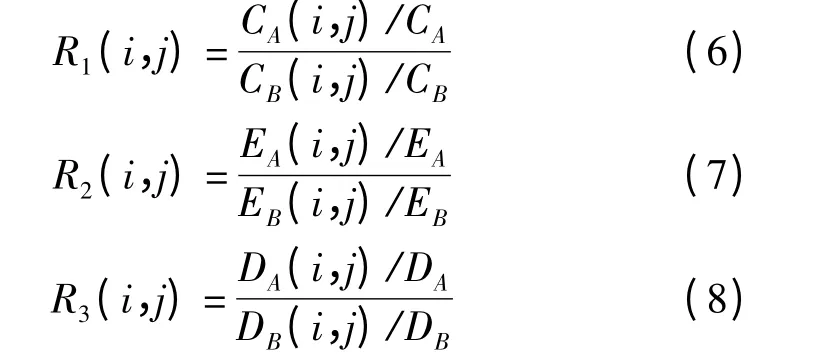
其中，CX，Ex，DX(X=A，B)分别表示整幅图像的清晰度、能量和方差;R1(i，j)表示了图像A，B 在该像素点的相对清晰度的高低，若R1(i，j)＞1，表明图像A 在该点的清晰度比图像B 高，反之，则图像B 在该点的清晰度更高。R2(i，j)，R3(i，j)与R1(i，j)的表征意义相同。

然后对同一像素点的邻域，计算得到R1、R2和R3的值，比较这3 个值，选择这3 个值中大的一个所对应的规则，作为此像素点的融合规则，得到融合图像的像素点。

3 实验及分析

本文实验对多聚焦钟表图像，多聚焦实验室图像采用Shearlet 变换结合多判决法进行融合处理，Shearlet 变换中采用非下采样拉普拉斯变换对图像进行多尺度分解，分解层数为4 层，采用Meyer 小波生成的Shear 滤波器对图像进行多尺度分解，分解方向数分别为6，6，10，10。为验证本文所用融合方法的有效性，实验分别采用清晰度判决，能量判决，方差判决和本文所用多判决法选择融合系数。采用不同判决方法得到多聚焦钟表融合图像如图1 所示。

图1 钟表聚焦图像4 种方法融合效果

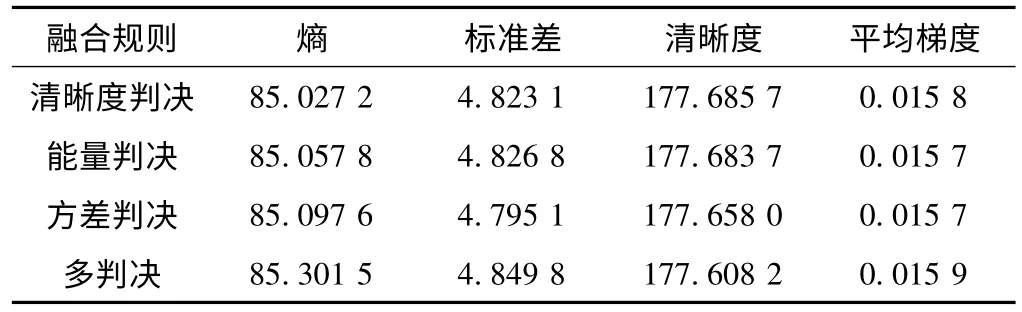
表1 基于不同融合规则的融合图像评价结果

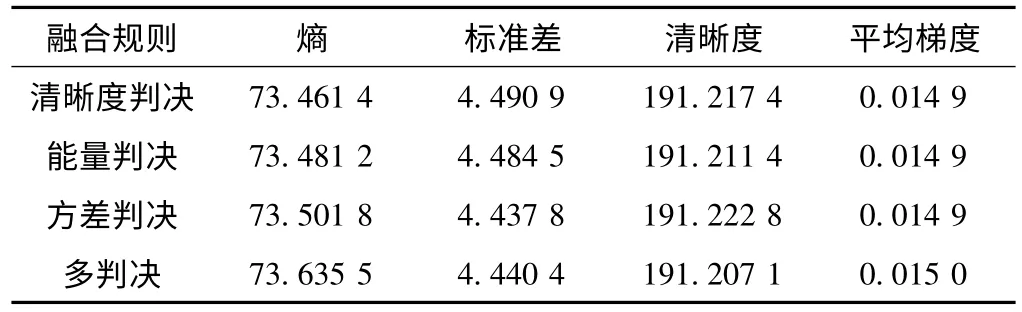
表2 基于不同融合规则融合图像评价结果

图2 实验室聚焦图像4 种方法融合效果

实验表明两组图像融合效果中多判决方法所获得的指标多数指标优于单个融合规则。

4 结束语

从图像的评价指标来看，采用任何单一规则来选择融合系数，均无较大差别，也没有一种融合规则的融合效果要明显高于另外两种，而结合3 个规则，采用多规则判决法来选择融合系数，避免了单一融合规则的缺点，所得到的融合图像，大部分指标都要优于单一图像，取得了比较好的结果，证明了此方法的有效性。

［1］ Artman H.Situation awareness and cooperation within and between hierarchical units in dynamic decision making［J］.Ergonomics，1999，42(11):1404－1417.

［2］ Daniel M M，Willsky A S.A multiresolution methodology for signal－level fusion and data assimilation with application to remotesensing［C］.Proceedings of the IEEE，1997，85(1):164－180.

［3］ Burt P J.Multiresolution image processing and analysis［M］.Berlin:Springer Verlag，1984.

［4］ Mallat S G.A Theory for multiresolution signal decomposition:the wavelet represeNtation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1989，11(7):674－693.

［5］ Do M N，Vetterli M.The contourlet transform:an efficient directional multiresolution image representation［J］.IEEE Transactions on Image Processing，2005，14(12):2091－2106.

［6］ Easley G R，Labate D，Lim W Q.Sparse directional image representations using the discrete shearlet transform［J］.Applied and Computational Harmonic Analysis，2008，25(1):25－46.

［7］ Lü Li，Zhao Jia，Sun Hui.Multi－focus image fusion based on shearlet and local energy［C］.Dalian，China:Proceeding of the 2010 2nd International Conference on Signal Processing Systems，IEEE，2010.

［8］ Gao Guorong，Xu Luping，Feng Dongzhu.Multi－focus image fusion based on nonsubsampled shearlet transform［J］.IET Image Processing，2013，7(6):633－639.

［9］ Yang Bin，Li Shutao.Multifocus image fusion and restoration with sparse repressentation［J］.IEEE Transactions on Instrumentation and Measurement，2010，59(4):884－892.

［10］Guo Kanghui，Labate D.Optimally sparse multidimensional representation using shearlets［J］.SIAM Journal of Math Anal，2007，39(1):298－318.

［11］赵嘉，孙辉，邓承志，等.基于粒子群优化的Shearlet 自适应图像去噪［J］.小型微型计算机系统，2011，32(6):1147－1150.