基于LMD 和SVM 算法的模拟电路故障诊断

钱 莉，姚 恒，刘 牮

(上海理工大学 光电信息与计算机工程学院，上海 200093)

随着电子电路集成化的日益提高，集成电路80%的故障来源于模拟电路，要在电路运行中对发生故障时准确及时地找出故障原因和位置，实现对电子系统的自动诊断和提高电子设备的可靠性有重要的意义和价值［1］。故障特征提取和分类器的选取是模拟电路故障诊断的关键技术。文献［2］直接采用采集的数据作为神经网络的输入，无需经过任何的预处理，因此需要一个更加复杂的神经网络和更长的网络训练时间。文献［3］通过输出采样信号的峭度和熵作为故障特征来训练SVM(Support Vector Machine)分类器。文献［4］使用了小波分解系数的能量指标作为特征向量来训练SVM 分类器。

LMD 算法是一种新的时频自适应分析方法［5］，与EMD 相类似，LMD 也是一种将复杂信号分解为多个简单信号之和的方法，都是基于极值点来定义局域均值函数和局域包络函数。但是对于包络函数的估计，LMD 算法通过滑动平均来代替3 次样条插值，可避免过包络、欠包络和虚假分量产生的问题。这种算法已经成功应用于脑电信号分析、机械设备的故障诊断［6－7］。本文将一种LMD 和SVM 相结合的新算法引入模拟电路的故障诊断。通过对采样数据进行LMD分解，然后求取分解得到的PF 分量的能量值，再结合支持向量机理论，将能量值作为模式识别的特征量输入到SVM 进行训练和预测，实现对模拟电路的故障诊断。仿真研究和实验数据分析表明了本文方法的有效性和可行性。

1 局域均值分解算法

LMD 算法本质上是从原始信号分解为若干个瞬时频率有物理意义的乘积函数，所有PF 均为单分量的调幅调频信号，每个PF 分量由一个包络信号和一个纯调频信号相乘得到，包络信号就是该PF 分量的瞬时幅值，纯调频信号可直接求出PF 的瞬时频率［8］。经过循环处理分解出所有的PF 分量。LMD 方法适合于分析多种类型的信号，包括EEG，功能性磁共振成像信号，地震信号等。

2 支持向量机SVM

支持向量机［9］统计学习理论提出的一种新的机器学习方法，其以结构风险最小化原则为理论基础，具有良好的泛化能力。将寻求分类间隔最大的优化问题转化为一个求解凸二次规划问题，所得解是唯一的全局最优解，避免了一般神经网络存在的局部极值问题。

对非线性问题，可通过某种非线性变换转换为某个高维空间的线性问题。结合泛函理论，在最优分类面求解中只要引入满足Mercer 条件的内积函数即核函数，便可实现非线性变换后的线性分类，而计算复杂度却没有增加。

采用不同的核函数可构造实现输入空间中不同类型的非线性决策面的学习机，从而导致不同的支持向量的算法，常用的核函数有线性核函数、多项式核函数、径向基核函数和Sigmoid 核函数。

3 模拟电路故障诊断算法与实例分析

3.1 基于LMD 和SVM 模拟电路故障诊断算法

基于LMD 和SVM 的模拟电路的故障诊断算法流程图如图1 所示，首先在电路系统正常和各种故障状态下，时域内采集观测点的输出信号，然后采用LMD算法［10］提取故障特征，一部分构成SVM 训练集，剩余部分构成SVM 测试集，用训练集训练分类模型，用测试集测试该模型的准确率，最终利用SVM 分类器计算平均准确率来返回故障诊断结果。

图1 算法流程图

3.1.1 LMD 算法

根据模拟电路中发生故障的性质，将模拟电路的故障分为硬故障和软故障两类。硬故障指元件参数发生较大的偏差如开路、短路故障;软故障指元件的参数超出预定的容差范围，一般不会使设备完全失效，但这类故障的征兆并不明显，一般故障特征提取方法并不能有效地提取出其故障特征。运用小波变换提取故障时，由于小波分解存在混频现象，导致提取信息的不准确。因此，采用LMD 算法提取模拟电路的故障特征。

LMD 的具体分解步骤见文献［6］，所谓PF 一般可表示为x(t)=a(t)cos(θ(t))，即幅值和相位随时间的变化而变化，当a(t)=1 时，x(t)便称为纯调频调幅信号，经LMD 分解后的信号可表示为

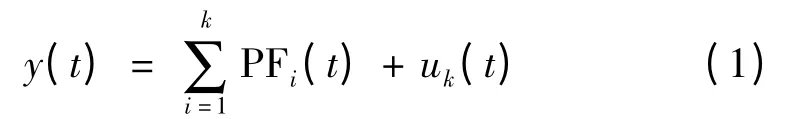
式中，PFi表示第i 个PF 分量;uk表示余项。其分解结果如图2 所示。

在特征提取部分，需要计算输出信号经LMD 分解后获得的前3 个PF 分量的能量值，对分解得到的PF分量，其能量定义如下

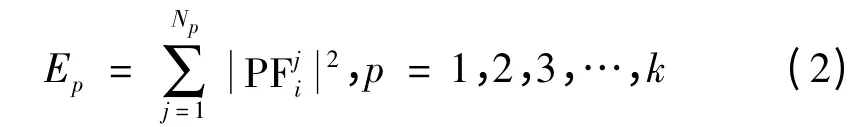
式中，p 表示分量的个数;PFji 表示第p 个PF 分量的第j 个数据点。根据能量的定义，求出每个PF 分量的能量值，构成模拟电路的故障特征值。

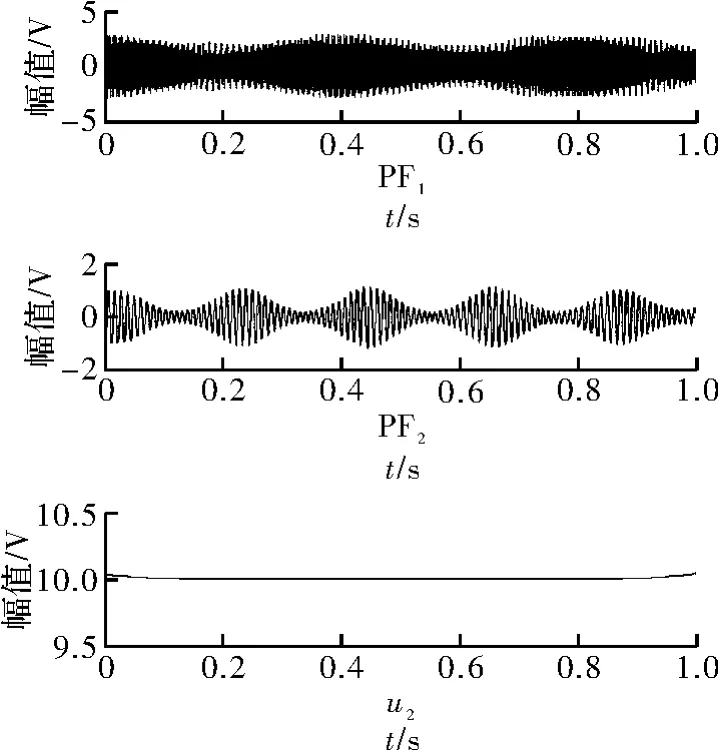
图2 信号分解结果

3.1.2 SVM 算法

为提高分类精度，可采用交叉验证法对SVM 的惩罚参数c 和核函数参数g 进行优化。在交叉验证法中，这里的c 和g 在以2 为底的指数范围网格内进行查找，先在大范围粗略寻找最佳的参数c 和g，再在粗略参数选择范围内进行更精细参数选择，从而获得一组最佳的参数c 和g。

设线性可分样本集为(xi，yi)，i=1，…，n，其中x∈Rd，y∈{+1，－1}是类别符号。求最优分类面的问题可转化为如下的约束优化问题

其中，w 是超平面法向量;b 为偏差。再利用Lagrange函数求解和最优化理论中KKT 条件，得到最优分类决策函数

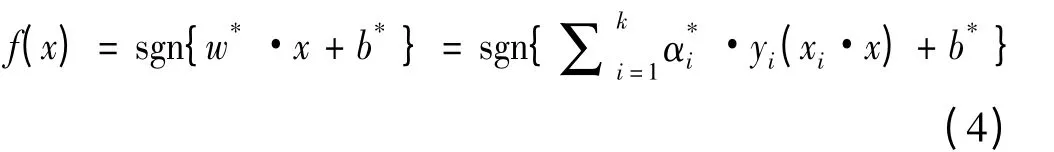
其中，α*和b*为确定最优划分超平面的参数;sgn 为符号函数，对于给定的未知样本x，只需根据f(x)的取值，即可判定所属的类型。

在线性不可分的情况下，SVM 通过核函数的非线性变换将低维输入空间的样本映射到高维空间，使其变为线性情况，并在该特征空间寻找最优分类超平面，以保证最小的分类错误率。此时的目标函数为

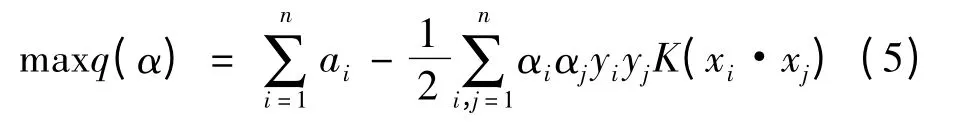
相应的分类函数

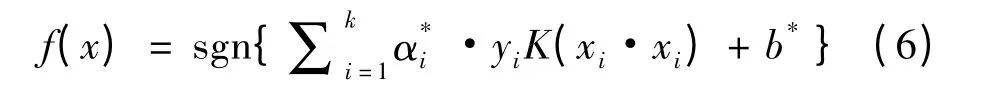
3.2 诊断实例与分析

为验证所提方法对模拟电路的诊断效果，选取带通滤波器作为诊断对象，选取3 个不同幅值与频率的正弦信号源V1，V2，V3，完成电路11 种状态模式的诊断。带通滤波器的电路结构和元件标称值分别如图3所示。

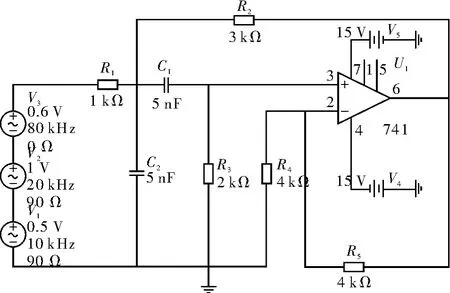
图3 带通滤波器电路

由于元件具有容差，在进行故障诊断时需要设定元件容差值，实验中需要在OrCAD/PSpice 软件中进行时域暂态分析和蒙特卡洛分析，设电路中电阻容差为标称值的5%，电容的容差为标称值的10%。假设电路中所有元件仅可能发生单故障，每个元件的故障值为X±50%X，其中X 为元件的标称值，则被测电路有10 种故障状态，加上正常状态(F0)共有11 种状态模式。

据LMD 算法获取电路不同工作状态下的故障特征向量。LMD 算法终止条件中的误差参数Δ=0.001，正常状态和R2+50%故障状态下分离出来的各PF 分量如图4 和图5 所示。从分解结果表1 可知，两种状态下的PF 分量由一定的差异，所以计算各PF 能量值能有效地区分故障特征，用来反映电路的故障状态。

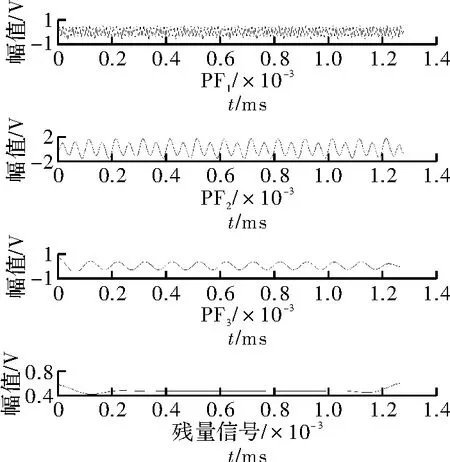
图4 正常状态下LMD 的分解结果

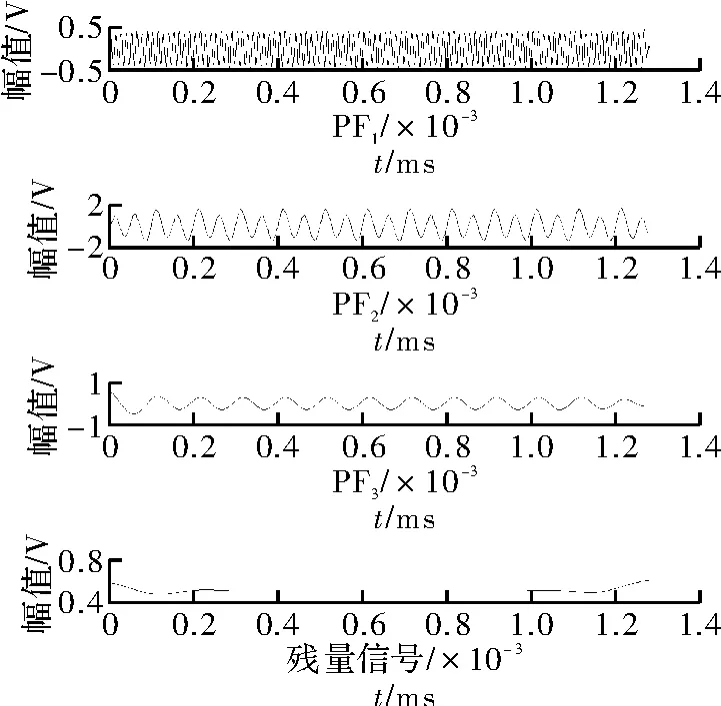
图5 R2+50%状态下LMD 的分解结果

表1 故障特征向量

采用交叉验证法，实验中SVM 交叉验证参数c 和g 的限定为以2 为底的指数，初始值为2－10，通过大范围寻找和小范围精细选择，得到最优参数c=2.828 4，g=2。支持向量机对测试样本的诊断正确率为98.27%。用支持向量机对带通滤波器的故障特征测试样本的诊断结果如表2 所示，其中，包含了每一类故障的诊断率和所有故障的平均诊断率。

表2 带通滤波器的故障诊断结果

4 结束语

故障特征提取对模拟电路故障诊断至关重要，其能影响分类器的设计及其性能。本文对如何获得更优的电路故障特征进行了研究，提出了基于LMD 算法的SVM 分类电路故障诊断方法。通过实验仿真结果可看出，对带通滤波器电路的故障诊断的正确率均在98%以上。

［1］ Milor L S.A tutorial introduction to research on analog and mixed－signal circuit testing［J］.IEEE Transactions on Circuits and Systems，1998，45(10):1389－1407.

［2］ Spina R，Upadhyaya S.Linear circuit fault diagnosis using neuromorphic analyzers［J］.IEEE Transaction on Circuits and System II:Express Briefs，1997，44(3):188－196.

［3］ Yuan L F，He Y G，Huang J Y，et al.A new neural－network－based fault diagnosis approach for analog circuits by using kurtosis and entropy as a preprocessor［J］.IEEE Transactions on Instrumentation ＆ Measurement，2010，59(3):586－595.

［4］ Zuo L，Hou L G，Zhang W，et al.Applying wavelet support vector machine to analog circuit fault diagnosis［C］.Wuhan:Second International Workshop on Education Technology and Computer Science，2010:75－78.

［5］ Jonathan S Smith.The local mean decomposition and its application to EEG perception data［J］.Proceedings of the Royal Society A，2008，464(3):1483－1501.

［6］ Smith J S.The local mean decomposition and its application to EEG perception data［J］.Journal of Royal Society Interface，2005，2(5):443－454.

［7］ 程圣军，杨宇，余德介.局域均值分解算法及其在齿轮故障诊断中的应用［J］.振动工程学报，2009，22(1):76－84.

［8］ 任达千，杨世锡，吴昭同，等.基于LMD 的信号瞬时频率求取方法［J］.浙江大学学报:工学版，2009，43(3):523－528.

［9］ 尉询楷，李应红，王硕，等.基于支持向量机的航空发动机滑油监控分析［J］.航空动力学报，2004，19(6):392－397.

［10］张亢，程军圣，杨宇.基于有理样条函数的局部均值分解算法及其应用［J］.振动工程学报，2011，24(2):96－103.