拟线性椭圆问题正解的存在性和不存在性

陈海鸿，杨芳萍

（1.陇东学院数学与统计学院，甘肃庆阳745000；2.兰州大学数学与统计学院，甘肃兰州730000；3.陇东学院信息工程学院，甘肃庆阳745000）

[数理科学与信息科学研究]

拟线性椭圆问题正解的存在性和不存在性

陈海鸿1,2，杨芳萍3

（1.陇东学院数学与统计学院，甘肃庆阳745000；2.兰州大学数学与统计学院，甘肃兰州730000；3.陇东学院信息工程学院，甘肃庆阳745000）

拟线性奇异椭圆方程；对流项；双参数；正解

讨论了Dirichlet边界条件下拟线性奇异椭圆方程

非线性奇异边值问题起源于研究化工多相催化的前后关系及化学催化剂动力学、导电材料的热传导理论、奇异极小曲面以及非牛顿流体、黏性流体的边界层现象等[1-5]。

当p=2,a=0时，M Ghergud等[6]假设奇异项g(t)在原点周围类似于t-α,α∈(0,1),在K(x)＜0,x∈且λ,μ＞0,问题(pλ,μ)在中有唯一解。另一方面，若K(x)＞0,x∈，存在λ*,μ*，使λ＞λ*或μ＞μ*时，问题(pλ,μ)在Σ中有解，当λ＜λ*且μ＜μ*时，问题(pλ,μ)在Σ中无解。M Ghergud等[7]证明了若K(x)＞0,x∈，g(t)在原点附近满足，仅当λ＞0足够大时，方程至少存在一个解。M Ghergud等[8]证明了若0＜a＜1则方程对所有的λ≥0至少有一古典解，若1＜a≤2则方程在λ较大时无解。p≠2,a=0的情形，通常采用变分法证明解的存在性及多重性[9-13]，含有对流项的奇异P-Laplace问题的研究论文不多。本文利用比较原理和上下解方法，得到了当λ,μ在某范围内时一类奇异拟线性椭圆问题解的存在性和非存在性的几个结果。

1 预备知识

本文考虑下面含有双参数和对流项的拟线性椭圆问题

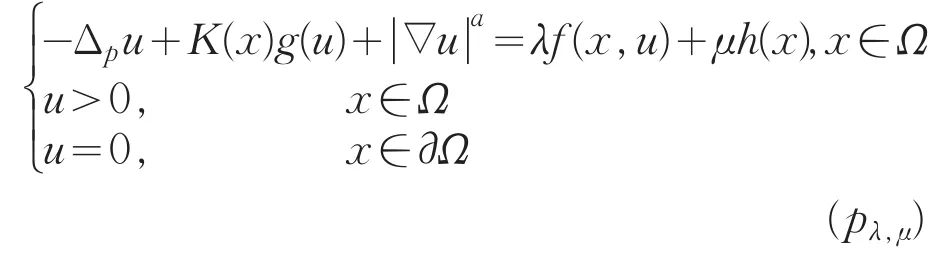
其中Ω⊂RN(N≥2)是有光滑边界∂Ω的有界区域，是p拉普拉斯算子，连续，关于第二个变量不减，关于第二个变量是次线性的，g∈C0,γ(0,∞),g＞0且不增，λ,μ是两参数。假定f,g满足下列假设。

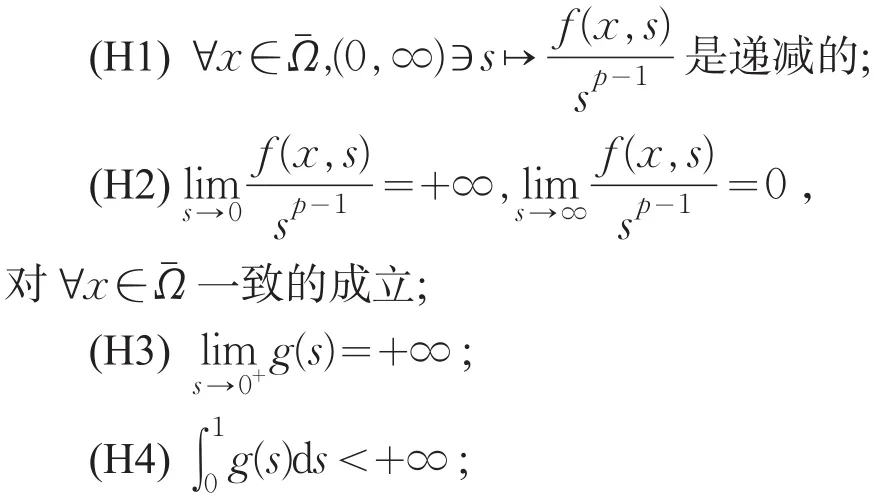
由(H4)可得如下的Keller-Osserman型条件

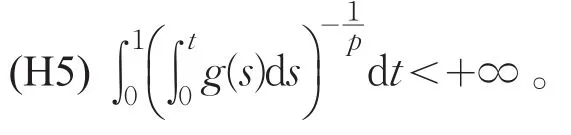
记λ1,φ1分别表示特征值问题

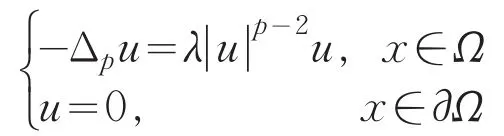
的第一特征值和对应于第一特征值的特征函数。

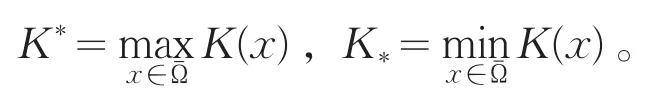
定义1非负函数u:Ω→(0,∞)称为问题(pλ,μ)的弱上解，是指u∈W1,p(Ω)，在∂Ω上u≥0，且

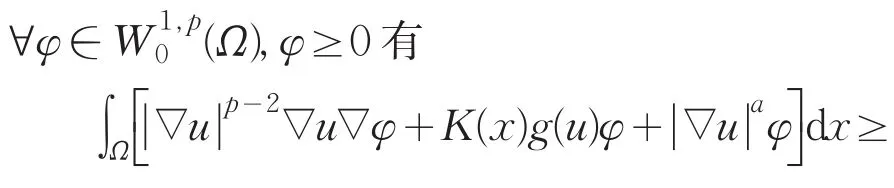
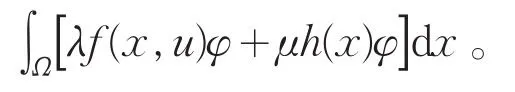
定义2非负函数u:Ω→(0,∞)称为问题(pλ,μ)的弱下解，是指u∈W1,p(Ω)，在∂Ω上u≤0，且有

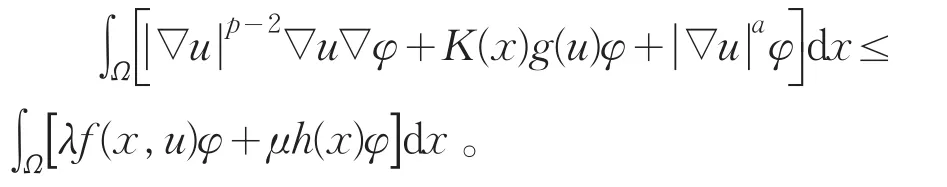
定义3非负函数u:Ω→(0,∞)称为问题(pλ,μ)的弱解，是指u∈W1,p(Ω)，且有

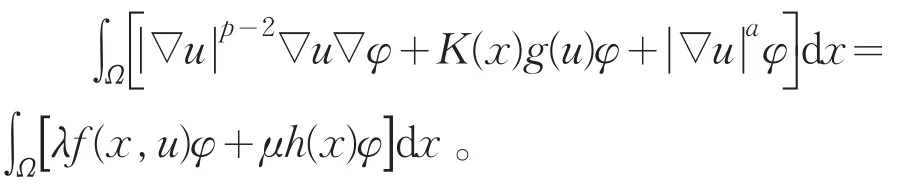
2 主要结果及证明

先证如下存在性定理。

设F满足如下条件：

(F1)F：×（0，∞）→R是×（0，∞）的任意紧子集上具有指数β()β∈(0,1)的Ho¨lder连续函数。

(F3)∀t＞0，存在常数D(t)＞0，使得∀x∈及r≥s≥t有

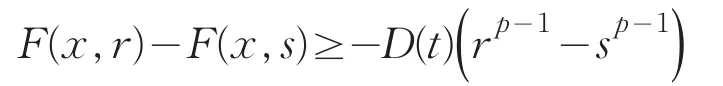
并且存在δ＞0和非空开子集Ω0⊂Ω，使得s∈(0,δ)有

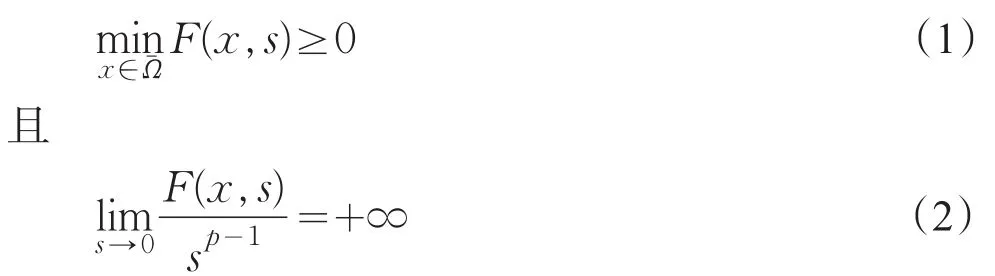
对x∈Ω0一致的成立。

定理1若F满足(F1)～(F3)，则对任意的非负函数φ0∈C1,β(∂Ω)，任意旳紧子集G⊂Ω⋂{x∈∂Ω:φ0＞0}问题

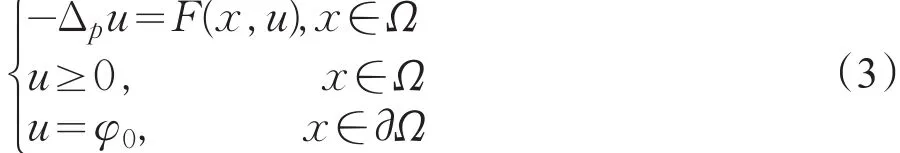
至少有一正解u∈C1,β(G)⋂C(Ωˉ)。

证明：考虑边值问题

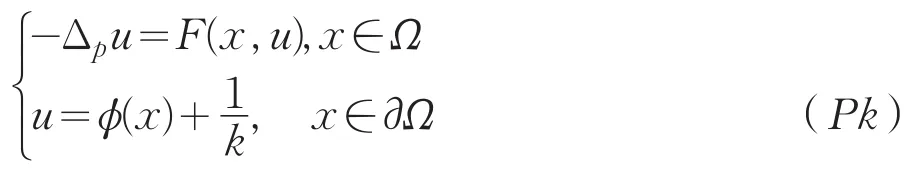
其中k为正整数。

记φm,k(x)(φm,∞(x))是如下问题的解

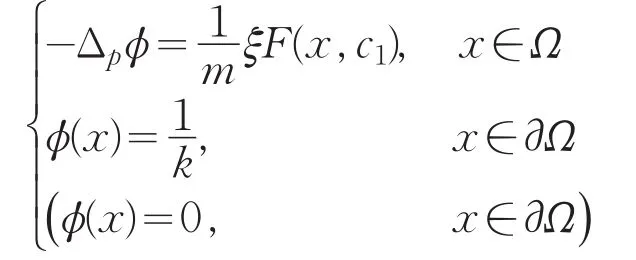
于是对所有的m,k≥1，有

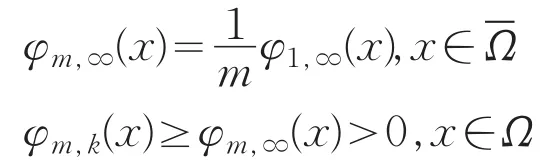
若x∈,m*≥m及k*≥k有

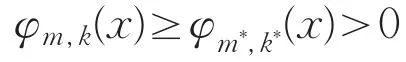
则存在d1,d2＞0，使得

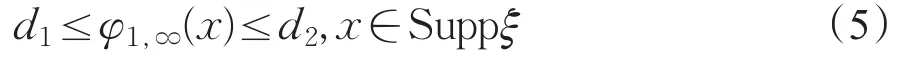
由Schauder估计，只要m,k充分大，可以使φm,k(x)很小对x∈一致的成立。从而，存在整数m0，由式（2）有

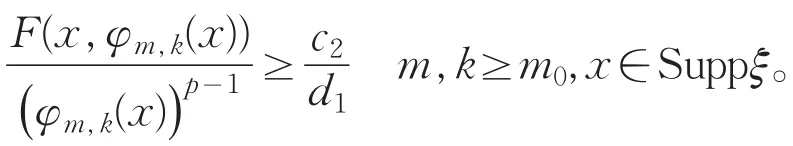
由式（1）得

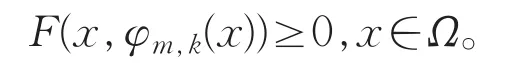
因此，若x∈Suppξ且m,k≥m0，对φ≥0，则由式（4）（5）有

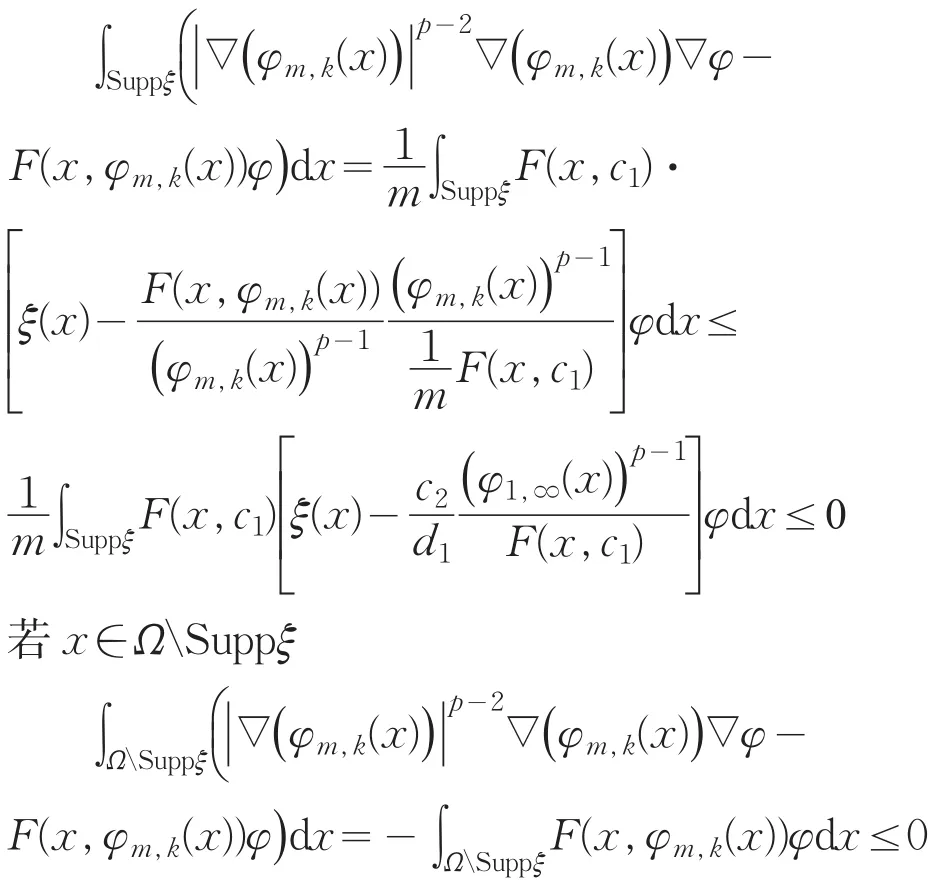
当m,k≥m0时，φm,k(x)是问题(pk)的一个弱下解。

记δk=，则有

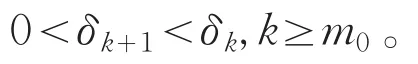
由（F2），取λ0＞0使得

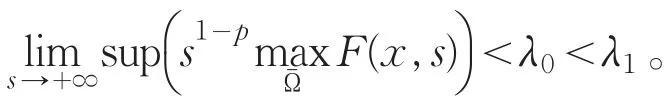
考虑如下问题

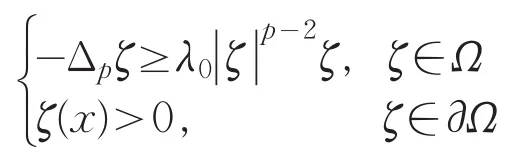
令k0是一充分大的正整数，可以验证对每个k≥m0,k0ζ(x)问题(pk)的一个弱上解，同时有

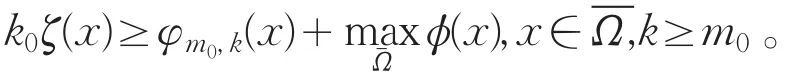
第二步：定义迭代如下

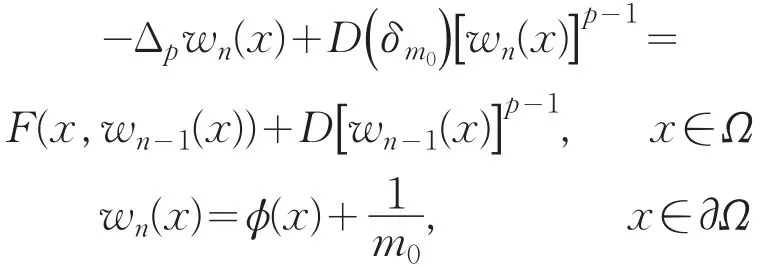
由（F3）得，∀x∈Ω,s↦F(x,s)+D(δm0)sp-1是上的增函数，取w0(x)=φm0,m0(x)或 (k0ζ(x))，可得一单调序列收敛到问题(pm0)的解um0(x)∈W1,p(Ω)，并有。用m0+1替换m0，取w0(x)=φm0,m0+1(x)或 (um0(x))，类似于上面的讨论可得问题(pm0+1)的正解um0+1(x)∈W1,p(Ω)，又由-Δp+D(δm0+1)的比较原理得

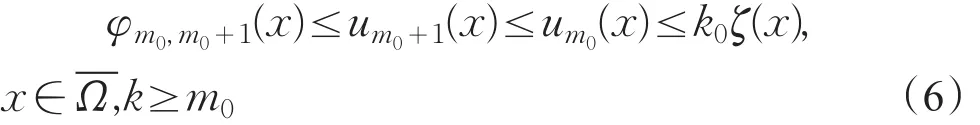
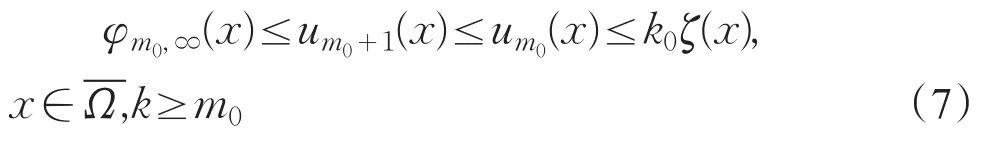
并且对任意k≥m0,uk(x)是问题(pk)的解。

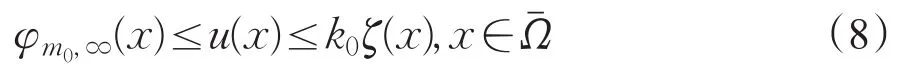
另一方面，由F的假设条件，存在数

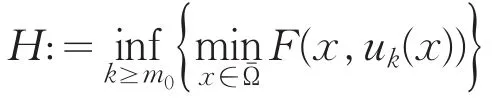
由比较原理有

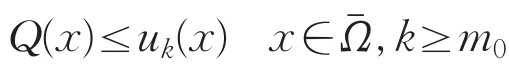
从而有

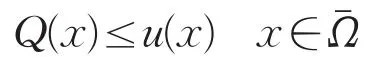
其中Q(x)是问题

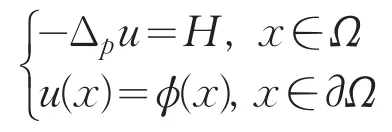
的解。若G是Ω⋃{x∈∂Ω|ϕ(x)＞0}的紧子集，存在两正数E1(G),E2(G)，使得

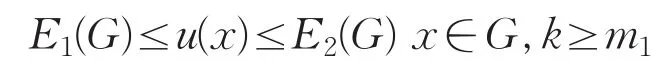
由Schauder理论和正则理论可得u(x)∈C1,β(G)是问题（3）的解。又若x0∈∂Ω，则对∀ε＞0,∃ρ＞0及整数m1≥m0，使得

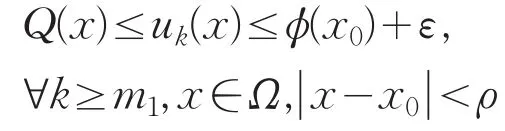
则u(x)在上连续并满足边界条件，定理得证。

定理2设K*＞0，f满足(H1)、(H2)；且，则对所有λ,μ＞0，问题(pλ,μ)无解。

证明：假设对λ,μ＞0问题(pλ,μ)有一解uλ,μ，由f满足(H1)、(H2)，由定理1得问题

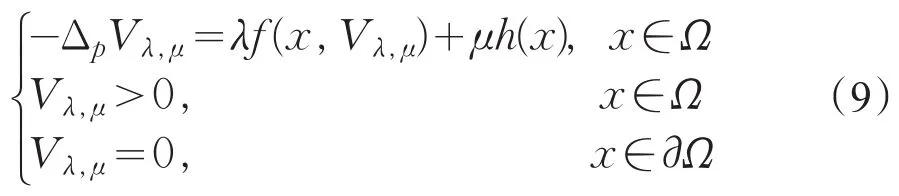
存在解Uλ,μ，并由性质2.1[12]知，根据文献[14]得∃c1,c2＞0，使得

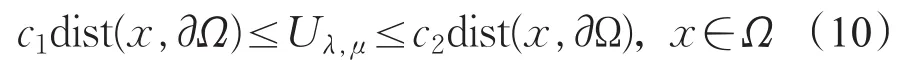
考虑扰动问题

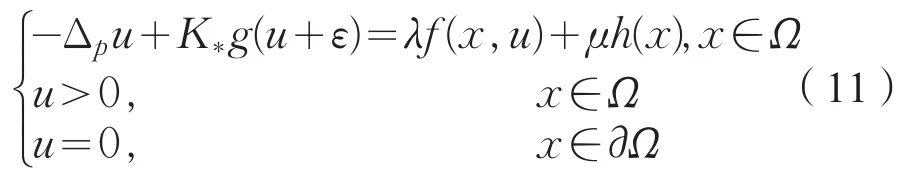
由于K*＞0，则uλ,μ和Uλ,μ分别是式（11）的下解和上解，又由得Uλ,μ∈L∞(Ω)，从而由比较原理[13]有uλ,μ≤Uλ,μ，由上下解迭代得式（11）的解

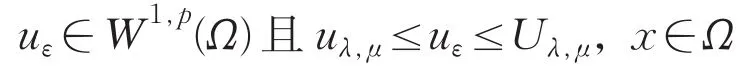
积分式（11）得

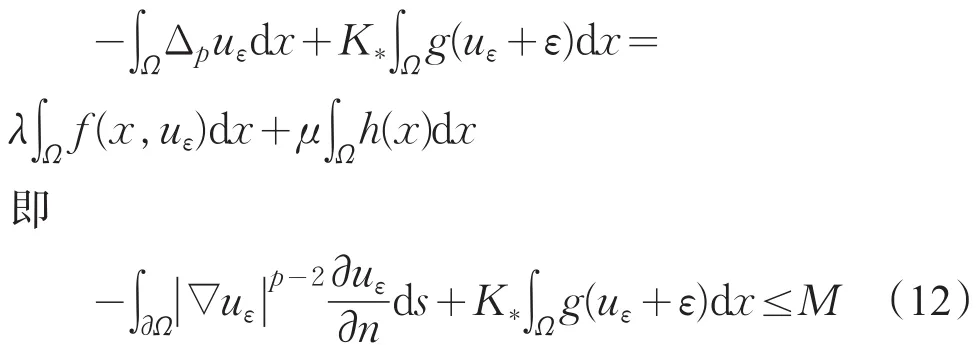
M＞0，考虑到，则可得

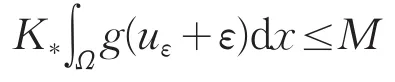
由于uλ,μ≤Uλ,μ，故有

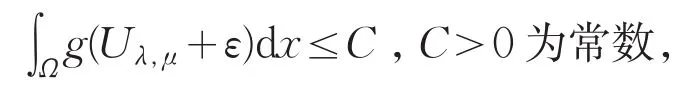
即对任一紧子集w⊂⊂Ω，有

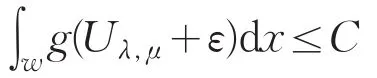
令ε→0+，可得

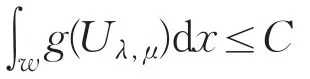
从而可得

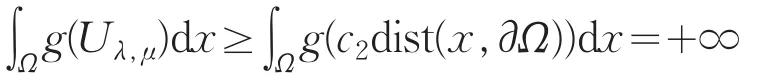
与式（13）矛盾，故问题(pλ,μ)无解。

定理3设K*＞0，f满足(H1)、(H2)；g满足(H3)、(H4)；则存在λ*,μ*＞0，使得

（Ⅰ）当λ＞λ*或μ＞μ*时，问题(pλ,μ)至少有一个解。

（Ⅱ）当λ＜λ*且μ＜μ*时，问题(pλ,μ)无解。

为证定理3，先证下面的引理：

引理1若f满足(H1)、(H2);g满足(H4)，则存在λ*＞0，使得对∀μ＞0，当λ＞λ*时，问题

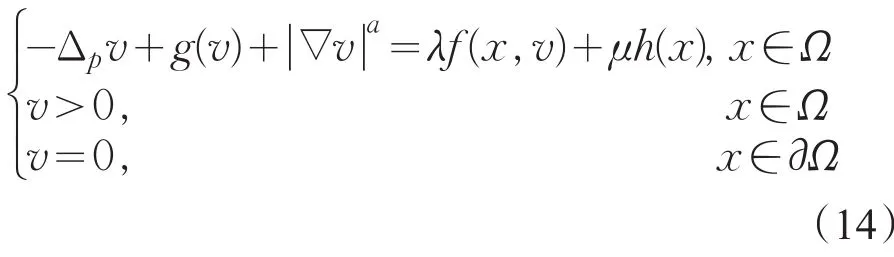
至少有一解vλ,μ。

证明：对μ＞0固定λ＞0，则由式（9）定义的Uλ,μ是问题（14）的上解，下面主要是找下解，有

令G(t)=，并记，则ψ(t)是增函数，记H(t)是ψ(t)的反函数，H:[0,∞)→[0,∞)满足

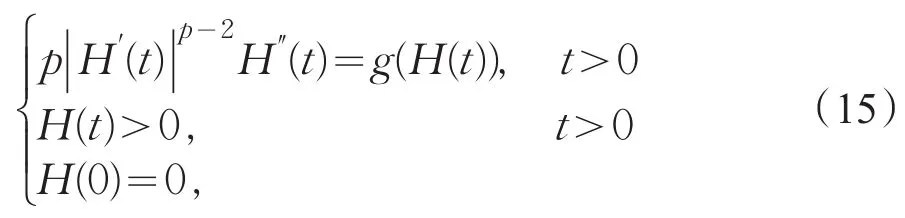
在式（15）两边乘以H′，然后在区间[s,t]积分得

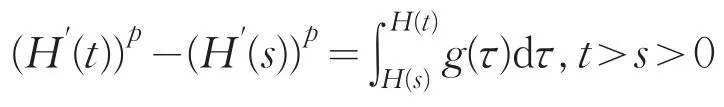
由(H4)及上式可将H′延拓到原点，即H′(0)=0，考虑到在(0,∞)上H′递增，H″递减，故有

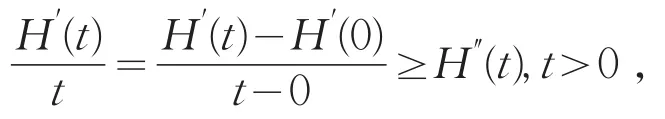
因此对t＞0有H′(t)≥tH″(t)，积分此不等式有

由强极大值原理，存在δ＞0,Ω0⊂⊂Ω，使得

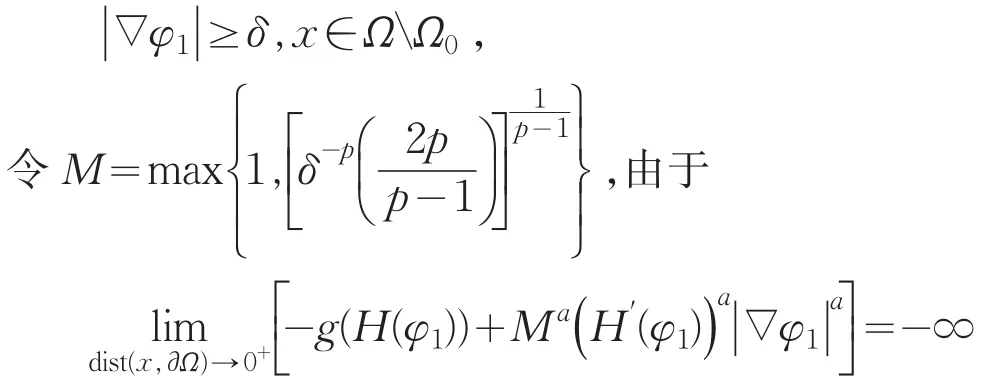
使Ω0充分逼近∂Ω，则有

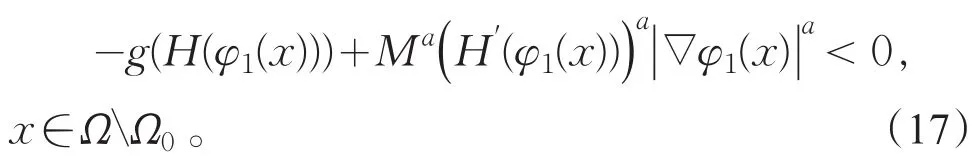
下证λ＞0充分大时，是式（14）的下解。取

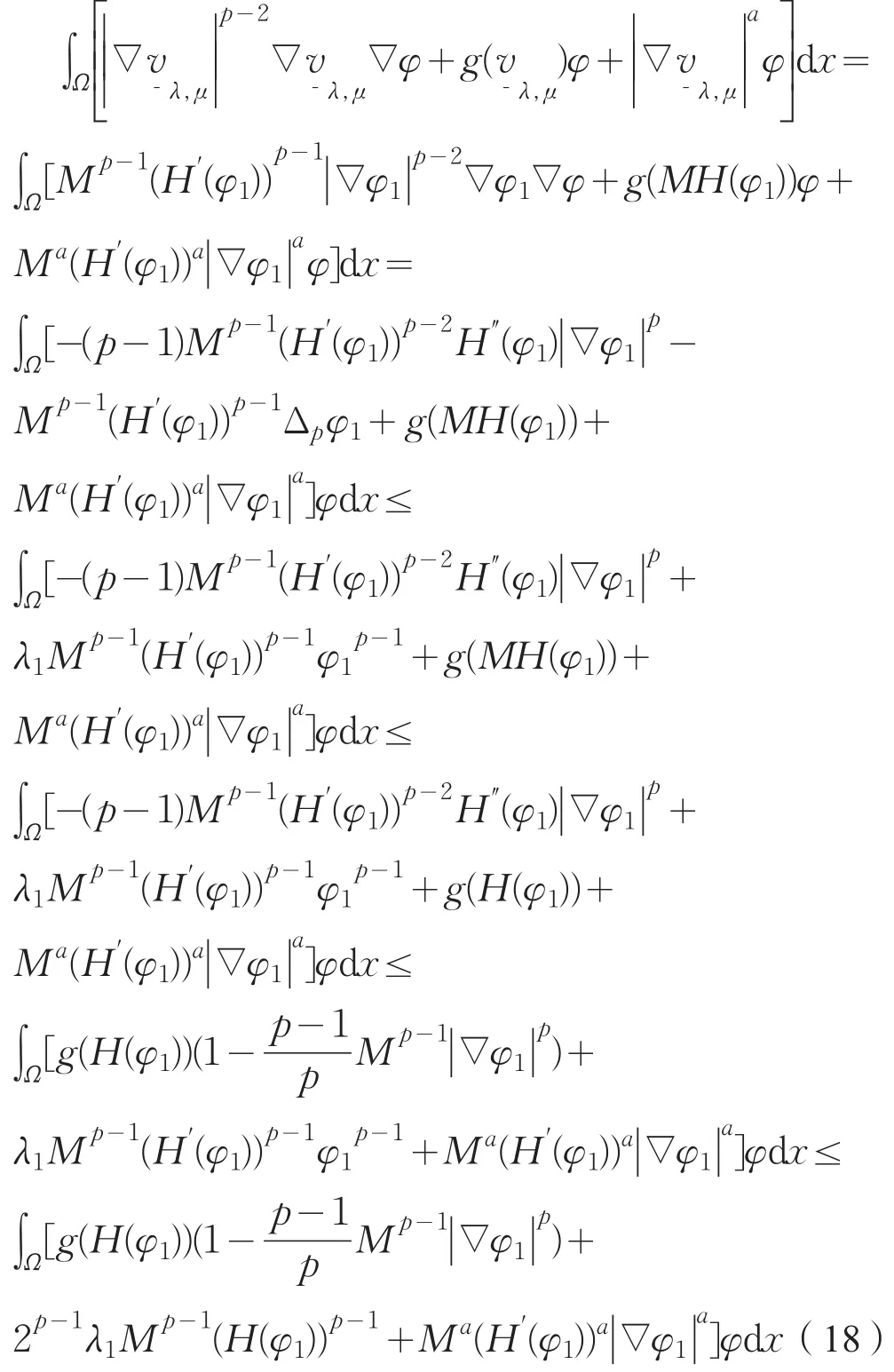
由M的定义及式（17）得

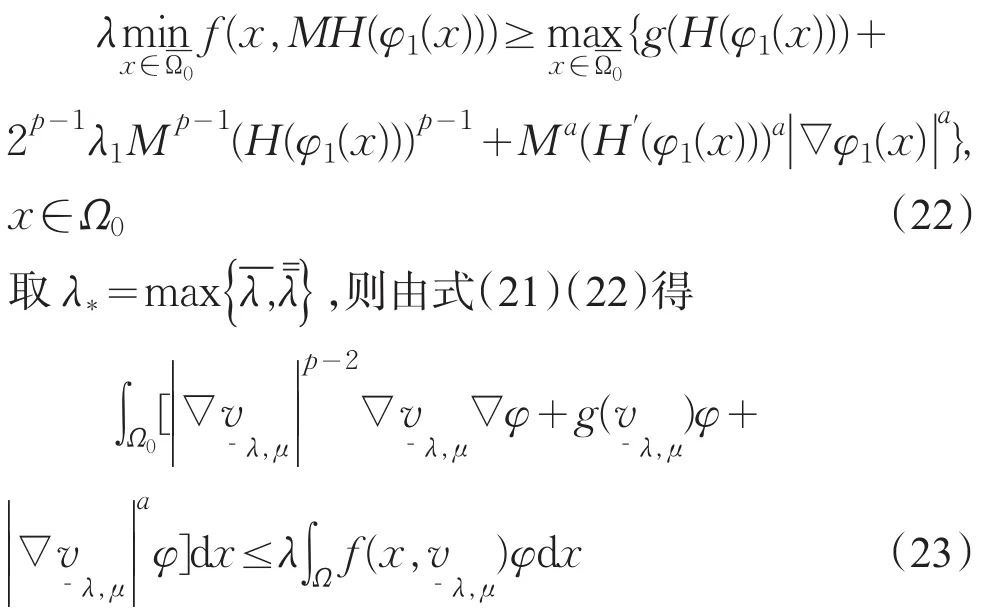
由式（20）（23）知λ＞λ*时，是问题（14）的下解。由比较原理[13]，在Ω上有，定理4.14[5]有λ＞λ*,∀μ＞0，问题（14）至少存在一个解vλ,μ∈W1,p(Ω)，使得。引理获证。

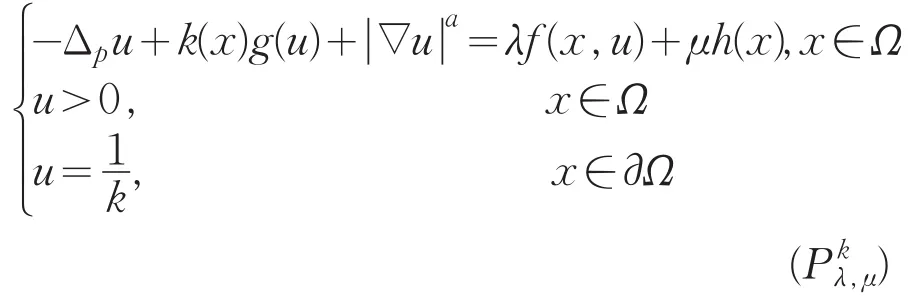
下面将证明分成以下几步。

第一步：当λ较大时(Pλ,μ)解的存在性。由引理1知，存在λ*＞0，对λ＞λ*，∀μ＞0，问题

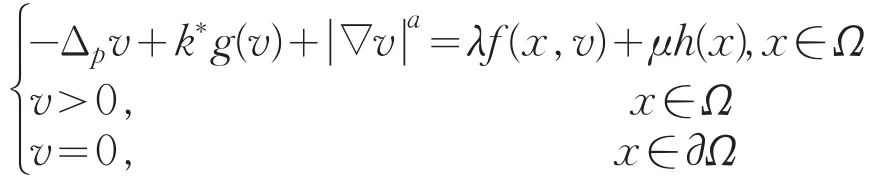
至少有一解vλ,μ，则是k≥1时，问题的弱下解，由定理1，令ω∈W1,p(Ω)是下列问题的弱解

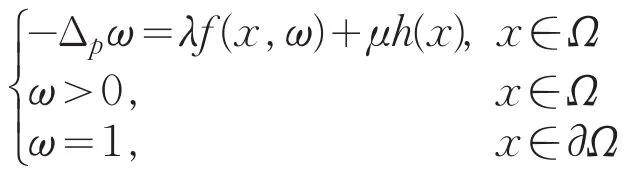
则ω是k≥1时问题的弱上解，由比较原理得在Ω上1≤v1≤ω，故可知问题有解，并有，取和v2是问题的一对上解和下解，可得的解并有继续此过程，可得解序列满足x∈，定义

下证uλ,μ是问题(Pλ,μ)的解，并满足

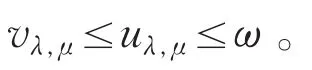
对任意D⊂⊂Ω及，由f,g的单调性，Hlder连续性及≤C[12]知

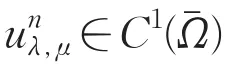
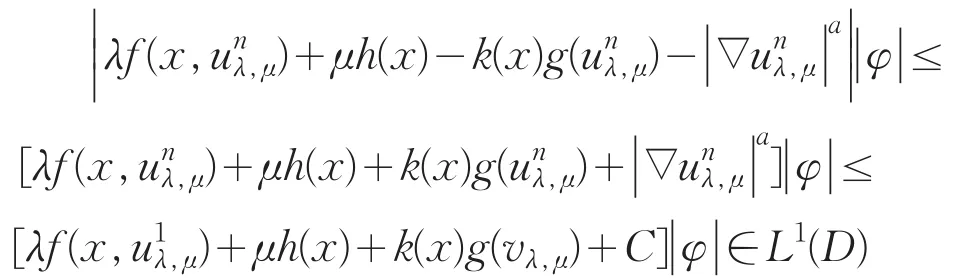
根据控制收敛定理有

即对λ＞λ*,∀μ＞0问题(Pλ,μ)至少有一解uλ,μ∈W1,p(Ω)。并由文献[8]知uλ,μ∈C1,γ(Ω)。

第二步：当μ较大时(Pλ,μ)解的存在性。由文献[15]的定理2，可得∃μ*＞0若μ＞μ*时，下面问题

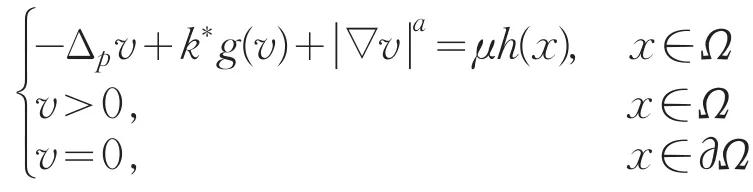
至少有一解vμ，记，可验证vk是问题的一个下解。类似于第一步可证当λ＞0,μ＞μ*时，问题(Pλ,μ)至少有一解。

第三步：当λ,μ均很小时(Pλ,μ)无解。令λ,μ＞0，由于k*＞0，记

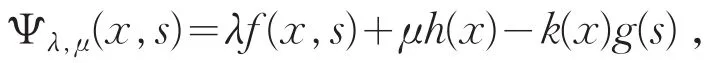
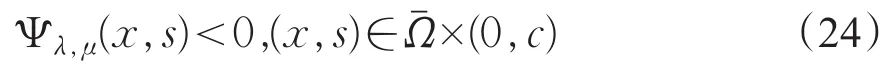
令s＞c，由(H1)可得

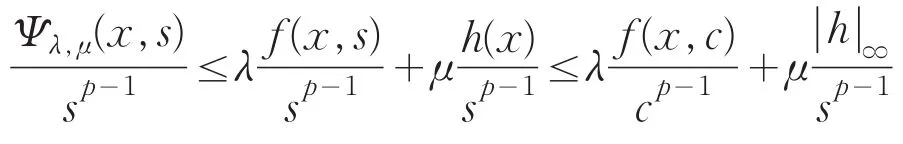
对x∈，固定，并令

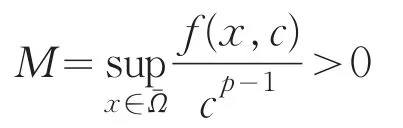
结合上面的不等式有

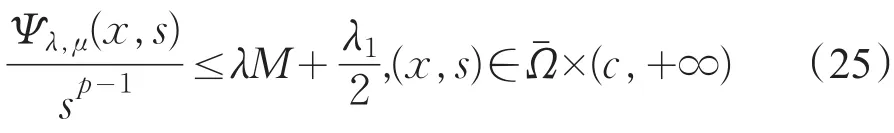
由式（24）（25）得

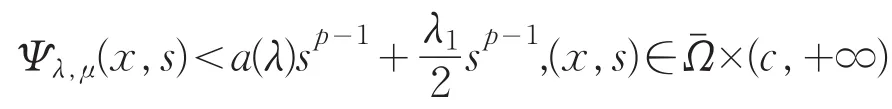
并且当λ→0时a(λ)→0。若问题(Pλ,μ)有一解uλ,μ。则

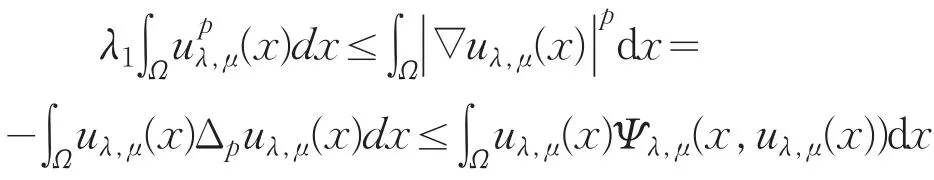
由式（25）有

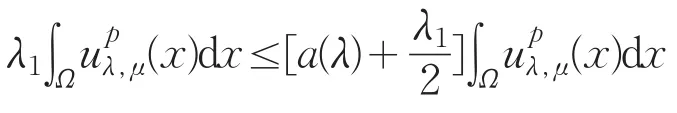
由于当λ→0时a(λ)→0，λ,μ＞0充分小时，上述关系式将导出矛盾。故当λ,μ均很小时(Pλ,μ)无解。

定理4设K*＞0，f满足(H1)、(H2)，则存在λ*,μ*＞0，对λ＞λ*或μ＞μ*时问题(pλ,μ)至少有一个解。

证明：固定λ＞0，由于k*＜0，则

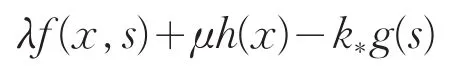
满足定理1的条件。因此问题

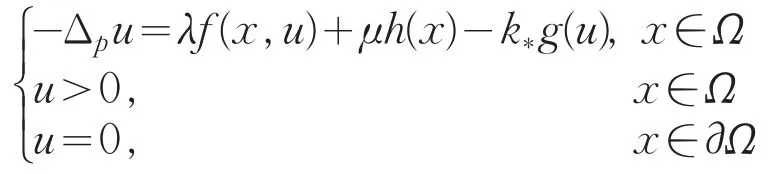
存在解uˉλ,μ(x)∈C1,γ(Ω)，且是问题(Pλ,μ)的一个上解。下面找问题(Pλ,μ)的一个下解。为此考虑问题

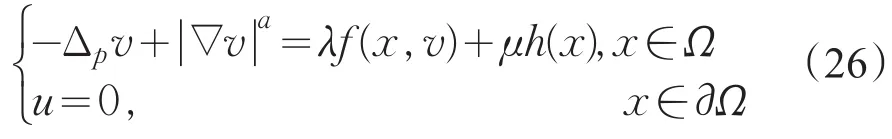
首先=0是问题（26）的下解。由定理1，下列方程

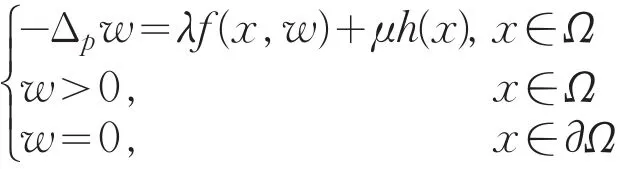
存在解w∈W1,p(Ω)，且w(x)＞0是问题（26）的上解，则问题（26）至少有一解v∈W1,p(Ω)，由文献[15]知，其中M是一常数，因此存在λ*,μ*＞0，当λ＞λ*或μ＞μ*时，可保证

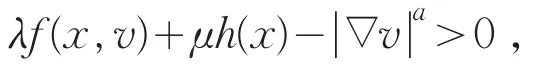
则可得v(x)＞0(x∈Ω)。即得是问题(Pλ,μ)的一下解，并对φ＞0有

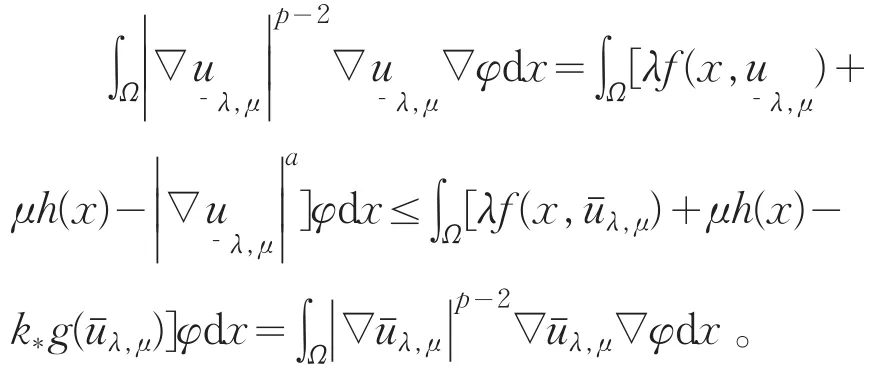
定理5设K*＞0＞K*，f满足(H1)、(H2)，g满足(H3)，则存在λ*,μ*＞0，对λ＞λ*或μ＞μ*时问题(Pλ,μ)至少有一个解。

证明：已知k*＞0，由定理3的证明知存在λ*,μ*＞0使问题

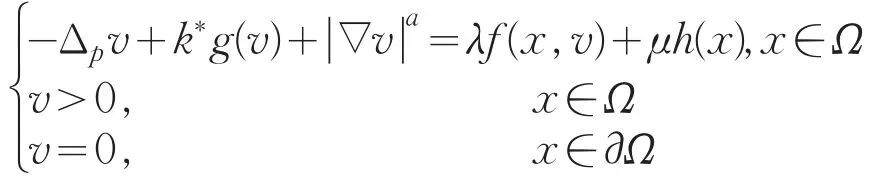
另一方面，由定理1知边值问题

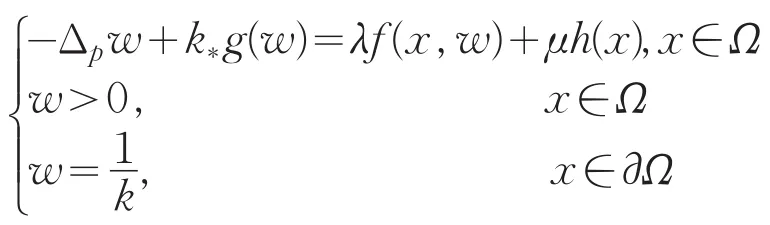
有一解wk(x)∈W1,p(Ω)，可以验证wk(x)是问题(Pλ,μ)的一个上解。由于k*＞0＞k*，可得

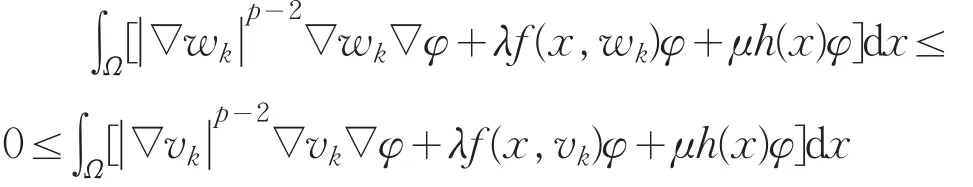
并且有vk(x)≤wk(x),x∈，由上下解讨论知存在一极小解满足v1(x)≤，取和v2为问题的一对上，下解，则问题存在一极小解W1,p(Ω)满足，重复此过程，可得问题的解序列，使得，定义uλ,μ(x)=，类似于定理3的证明可得uλ,μ(x)∈是问题(Pλ,μ)的解。定理得证。

[1]ALLEGRETTO W，HUANG Y X.Principal eigenvalues and Sturm comparison via Picone’s identity[J].Journal of Differential Equations，1999，156(2):427-438.

[2]COCLITE M M，PALMIERI G.On a singular nonlinear Dirichlet problem[J].Communications in Partial Differential Equations，1989，14(10):1315-1327.

[3]DIAZ G，LETELIER R.Explosive solutions of quasilinear elliptic equations:existence and uniqueness[J].Nonlinear Analysis:Theory，Methods&Applications，1993，20(2): 97-125.

[4]GILBARG D，TRUDINGER N S.Elliptic partial differential equations of second order[M].springer，2001.

[5]LIEBERMAN G M.Boundary regularity for solutions of degenerate elliptic equations[J].Nonlinear Analysis:Theory，Methods&Applications，1988，12(11):1203-1219.

[6]GHERGU M，RÂDULESCU V.Sublinear singular elliptic problems with two parameters[J].Journal of Differential Equations，2003，195(2):520-536.

[7]GHERGU M，RÂDULESCU V.On a class of sublinear singular elliptic problems with convection term[J].Journal of Mathematical Analysis and Applications，2005，311(2): 635-646.

[8]GHERGU M，RÂDULESCU V.Multi-parameter bifurcation and asymptotics for the singular Lane–Emden–Fowler equation with a convection term[J].Proceedings of the Royal Society of Edinburgh:Section A Mathematics，2005，135(1): 61-83.

[9]AGARWAL R P，PERERA K，O’REGAN D.A variational approach to singular quasilinear elliptic problems with sign changing nonlinearities[J].Applicable Analysis，2006，85 (10):1201-1206.

[10]PERERA K，SILVA E A B.Existence and multiplicity of positive solutions for singular quasilinear problems[J].Journal of Mathematical Analysis and Applications，2006，323 (2):1238-1252.

[11]PERERA K，SILVA E A B.On singular p-laplacian problems[J].Differntial and Integral Equations-athens，2007，20 (1):105.

[12]PERERA K，ZHANG Z.Multiple positive solutions of singularp-Laplacianproblemsbyvariationalmethods[J]. Boundary Value Problems，2005(3):377-382.

[13]MOHAMMED A.Positive solutions of the p-Laplace equation with singular nonlinearity[J].Journal of Mathematical Analysis andApplications，2009，352(1):234-245.

[14]GUI C，LIN F H.Regularity of an elliptic problem with a singular nonlinearity[J].Proceedings of the Royal Society of Edinburgh:SectionAMathematics，1993，123(06): 1021-1029.

[15]OL'GA A L，URAL'CEVA N N.Linear and quasilinear elliptic equations[M].Academic Press，1968.

Existence and Nonexistence of Positive Solutions of Quasilinear Elliptic Problems

CHEN Haihong1,2，YANG Fangping3
(1.School of Mathematics and Statistics,Longdong University,Qingyang 745000,Gansu,China; 2.School of Mathematics and Statistics,Lanzhou University,Lanzhou 730000,Gansu,China; 3.College of Information Engineering,Longdong University,Qingyang 745000,Gansu,China)

The existence and nonexistence of positive solutions of quasilinear singular elliptic prob-under Dirichlet boundary condition was discussed.By using the unbounded ofg(u)at zero and the signs of the extremal values of potentialk(x)on.We apply the comparision principle and sub-supersolution method to obtain the existence and nonexistence results of positive solutions for certain range of parametersλandμ.

quasilinear singular elliptic equation；convection term；two parameters；positive solution

O177.91

A

1672-2914（2015）02-0024-08

2014-12-13

甘肃省教育科学“十二五”规划基金项目（GS[2013]GHB0933,GS[2013]GHB1079）；陇东学院青年科技创新项目（XYLK1301）。

陈海鸿（1977-），男，甘肃天水市人，陇东学院数学与统计学院讲师，硕士，主要研究方向为非线性泛函分析。