电铁牵引负荷的构成分析及其功率模型
张 浩,熊浩清,陈 谦,鞠 平
(1.河海大学能源与电气学院可再生能源发电技术教育部工程研究中心,南京210098;2.国网河南省电力公司电力调度控制中心,郑州450052)
电气化铁路因其具有良好的经济优势和社会效益在我国发展迅速。尤其是从2008 年至今,中国建成了多条时速300 km/h 以上的高速铁路,标志着我国高速铁路时代的到来[1]。电铁单组设备的牵引功率越来越大,如京广高铁、郑西高铁等线路上运行的CRH380AL 型动车组牵引功率可达到21.56 MW。由于电铁牵引负荷在电力负荷中的比例越来越高,牵引变的电压等级也逐步从原来的110 kV 提高到220 kV[2]。
电铁牵引负荷与一般电力负荷最大的区别在于其随机波动性、冲击性和不对称性[3]。目前对牵引负荷的研究主要集中在谐波、负序等电能质量问题上[4-6],针对牵引负荷功率与电气模型的研究较少。文献[7-8]提出基于电铁牵引供电系统实际负荷构成特性的“感应电动机并联牵引电机和恒阻抗”机理负荷模型。文献[9]将二次侧牵引负荷变换至一次侧,建立一种将牵引负荷等效变换为所接入系统高压侧短时故障模型。上述模型均属于电气特性模型,本质上属于被动模型[10],并且模型的研究对象多为交直型电铁机车,而目前列车普遍为交直交型,其负荷电气特性存在较大差异。
电铁牵引负荷是“自变负荷”,即负荷内部会自主变化。自变期间,实质上是负荷内部特性发生变化,引起外在表现出的功率变化[10]。为了更好地反映电铁牵引负荷的随机波动性和冲击性,研究牵引负荷自变特性对电网的影响,需建立电铁牵引负荷的功率模型。文献[11]基于最小二乘支持向量机建立了交流传动牵引负荷的非机理模型,研究了牵引负荷的冲击特性,但无法反映牵引负荷的随机波动性。文献[12-13]提出一种利用概率模型描述牵引变有功功率和无功功率的方法,该方法针对较长的时间框架进行了研究,不利于分析牵引负荷对电网的动态影响。因此,分析电铁牵引负荷的构成,并对其建立分钟级功率模型对电网的安全稳定运行具有重要意义。
本文将牵引负荷功率波动分解为阶跃分量、低频缓坡分量与高频随机分量,分别对各个分量建模后合成,建立了基于时间序列的牵引负荷功率模型,并采用现场数据进行了应用,验证了方法的有效性。
1 电铁牵引负荷构成分析

图1 电铁牵引负荷结构Fig.1 Structure of traction load
电铁牵引负荷由牵引变电站、牵引网、电力机车等部分组成[3],如图1 所示。牵引变压器是牵引变电站的主要设备,其功能为降压、分相并为牵引负荷供电。高速铁路牵引变压器主要采用V/v 接线,一次侧额定电压一般为220 kV,二次侧额定电压为27.5 kV,直接与牵引网相连。牵引网以AT(auto transformer,自耦变压器)供电方式向电力机车供电。目前我国电力机车主要分为交-直型和交-直-交型两类。高速铁路上的电力机车均为交直交型,其通过PWM 整流器,将从牵引网上引入的单相交流电变成直流电,然后再将直流电逆变为频率和幅值均可调节的三相交流电供三相异步牵引电动机使用[14]。
由电铁牵引负荷的结构可知,牵引负荷功率主要由牵引变供电区域内的电力机车牵引功率叠加而成,并受牵引网、无功补偿装置等多种因素的影响。图2 所示为牵引负荷有功功率P 与无功功率Q 随时间变化的曲线,时间跨度为1 d。0~6 h,牵引变供电区域内没有机车运行,故有功功率和无功功率均为0。当有电力机车正常驶过牵引变供电区域时,牵引负荷吸收功率;而当电力机车处于电气制动模式时,牵引负荷会发出功率。由图2 所示的功率曲线可知,牵引负荷功率波动与其自身运行状态密切相关,所以重点研究其自变特性。
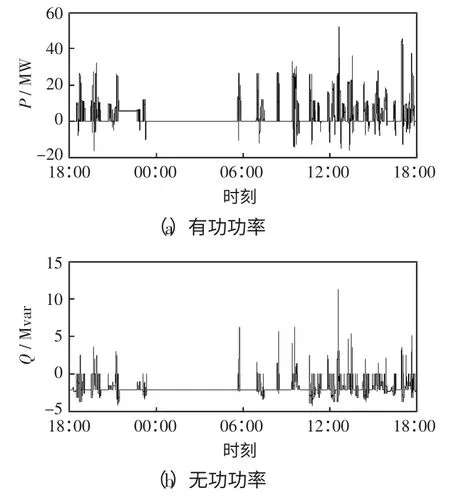
图2 电铁牵引负荷功率随时间变化曲线Fig.2 Curves of traction load power with time
图3所示为电力机车经过牵引变供电区域时,牵引负荷的功率波动曲线,即图2 中12:30—12:50 的放大图。由图3 可见,电铁牵引负荷主要存在以下几种形式的功率波动。
1)阶跃型波动
造成这种波动的主要原因是牵引变供电区域内运行电力机车数目的变化,其特点是功率变化速度快,波动幅值大,呈阶跃型。
2)低频缓坡型波动
造成这种波动的主要原因是电力机车运行速度、运行模式的变化,其特点是功率变化较平缓,波动幅值也相对较小。
3)高频随机波动
高频随机波动是由于测量误差、机车运行环境、运行状态微小变化等原因造成的较小扰动,其特点是功率变化频率高,波动幅值小。
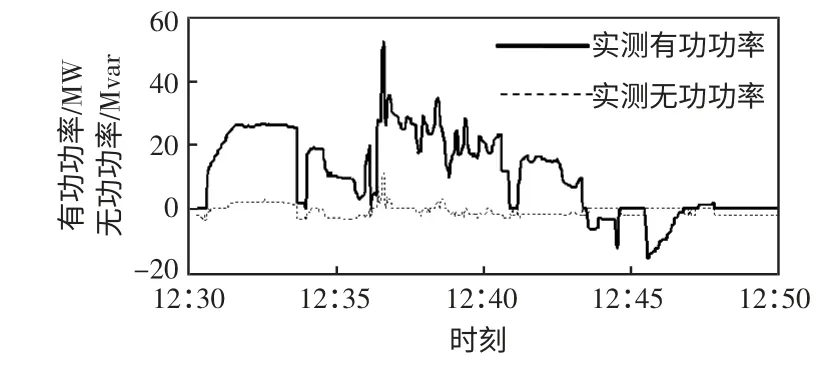
图3 电铁牵引负荷功率波动曲线Fig.3 Curves of traction load power
2 时间序列功率模型
特殊负荷模型分为电气特性模型和功率特性模型[14-15]。电气特性模型是负荷某一个时刻的电气模型,一般以电压作为输入,以有功功率、无功功率作为输出。功率特性模型,是较长一段时间(分钟级到小时级)的功率波动模型,没有输入变量,是一种自变的时间序列模型。
为了描述电铁牵引负荷的功率特性,可采用自回归滑动平均ARMA(auto-regressive and moving average model)模型建模[16-17]。
p 阶自回归q 阶滑动平均混合模型ARMA(p,q)模型可以描述为

式中:φj(j=1,2,…,p)为模型的自回归参数;θj(j=1,2,…,q)为模型的滑动平均参数;Xt为模型输出的功率序列;At为零均值零方差白噪声。
为避免数据过大或过小影响计算精度,对原始电铁牵引负荷功率序列{Xt}进行标准化处理:

功率序列{Xt}的长度为功率序列{Xt}的标准差,
电力机车在一个供电区域内运行的时间一般为几百秒,故可以选取几百秒的功率数据作为时间序列功率模型的自变量。对原始功率数据进行标准化处理后,按照赤池信息量准则AIC(akaike information criteria)准则对ARMA 模型进行定阶,确定p 与q 的值,再用矩估计计算参数φj和θj,最终建立ARMA 模型。
最后,将计算得到的数据进行还原为

3 电铁牵引负荷功率模型
3.1 基本原理
电铁牵引负荷功率模型如图4 所示。
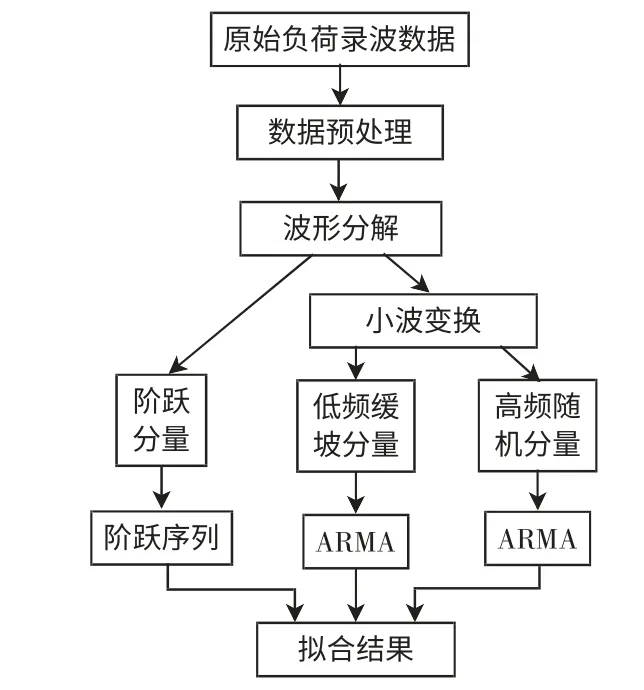
图4 电铁牵引负荷功率模型Fig.4 Power model for traction load
首先对牵引变原始负荷录波数据进行预处理,再对处理后数据进行分解:先基于波形,分解出由于电力机车驶入、驶出牵引站供电区域或换相引起的阶跃型波动分量,即阶跃分量;再对余下的功率分量用小波变换分解为低频缓坡分量和高频随机分量。这3 种分量分别对应电铁牵引负荷的3 种功率波动形式。然后对分解得到的阶跃分量用阶跃序列建模并拟合;对低频缓坡分量和高频随机分量,分别用ARMA 模型建模并拟合。最后对拟合后的3 种分量合成,得到功率最终拟合值。
3.2 波形分解方法
电铁牵引负荷的功率波动与机车的驶入、驶出,线路坡道、曲线、站场、限速、轨道、天气、司机操作等都直接相关[18]。当牵引变供电区域只有单列电力机车运行时,牵引负荷有功功率波动如图5所示。无功功率波动与有功功率波动类似。图中,T1为电力机车驶入牵引变供电区域开始运行至稳态的功率上升时间;T2为电力机车驶出牵引变供电区域功率下降时间;T3为电力机车在牵引变供电区域内运行的时间;P1为无电力机车时的功率损耗,接近为0;P2为电力机车驶入牵引变供电区域时的功率增量;P3为电力机车驶出牵引变供电区域时的功率负增量。
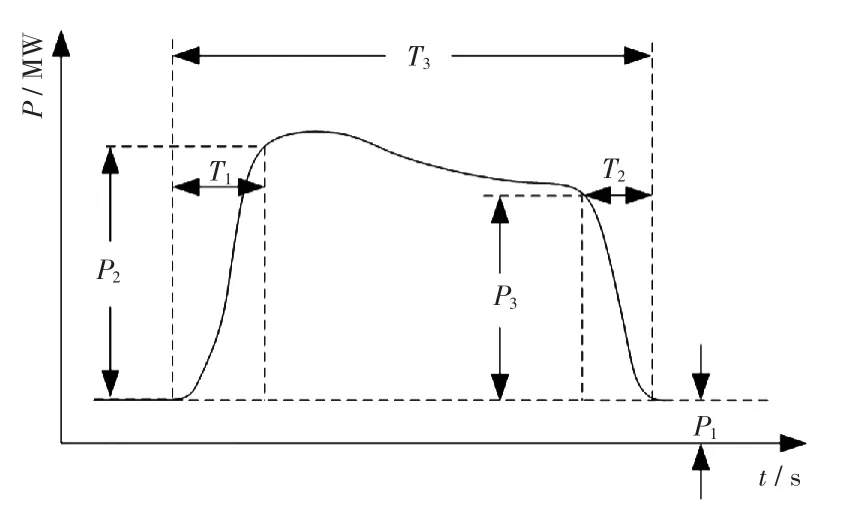
图5 单列电力机车运行时牵引负荷有功功率波动Fig.5 Active power curve of single electric locomotive
由此,可设定电铁牵引负荷的功率波动是否为机车驶入或驶出造成的判断条件为

式中:Tin为电力机车驶入牵引变供电区域的最长时间,一般在4~15 s;Tout为电力机车驶出牵引变供电区域的最长时间,一般在1.5~5 s;P0为最小阶跃功率,对于高速铁路P0〉5 MW。当牵引负荷功率波动满足式(4)时,判断当前有电力机车驶入牵引变供电区域;当满足式(5)时,判断当前有电力机车驶出牵引变供电区域。根据设定的判断条件可对牵引负荷原始功率录波数据进行波形分解。
3.3 小波变换
小波变换WT(wavelet transform)是一种时频局部化分析方法,其时间窗和频率窗的窗口大小固定不变,但其形状可变。小波变换通过平移母小波可获得信号的时间信息,而通过缩放小波的宽度可获得信号的频率特性[19-20]。
连续小波变换的定义为

式中:a 为缩放因子,对应于频率信息;b 为平移因子,对应于时空信息;ψ(x)为小波函数,即母小波;ψ*(x)表示ψ(x)的复共轭。
工程上常采用离散小波变换。将连续小波变换的缩放因子a 与平移因子b 同时离散化,即可得到离散小波变换。选取合适的母小波,对原始功率录波数据进行离散小波变换,即可将其分解为低频缓坡分量和高频随机波动分量。
3.4 阶跃序列
阶跃型波动主要是由牵引变供电区域内电力机车数目变化造成的。电力机车驶入或驶出牵引变供电区域造成的功率波动近似于阶跃函数的叠加,可表示为惯性环节对阶跃激励u(t)响应:

式中,Ts为时间常数。则阶跃分量可表示为

式中,Ki为惯性环节阶跃响应的增益。
4 应用实例
根据牵引变实测牵引负荷功率录波数据,分别选取牵引变供电区域内只有单列机车和有多列机车交汇时的功率数据进行建模。由于电气化铁路尤其是高速铁路功率因数很高(接近于1),且存在较多无功补偿设备,牵引负荷无功功率波动较小,分析时只考虑有功功率。实测牵引负荷录波数据采样时间间隔为1 s。
首先,对牵引变原始录波数据进行波形分解,得到阶跃分量。然后基于小波变换,分解得到低频缓坡分量与高频随机分量。单列机车时牵引负荷有功功率分解如图6 所示,多列机车交汇时牵引负荷有功功率分解如图7 所示。
得到牵引负荷的3 类分量以后,对阶跃分量用阶跃序列建模并拟合;对低频缓坡分量与高频随机分量进行标准化处理,分别用ARMA 模型建模并拟合。
定义一致性系数为
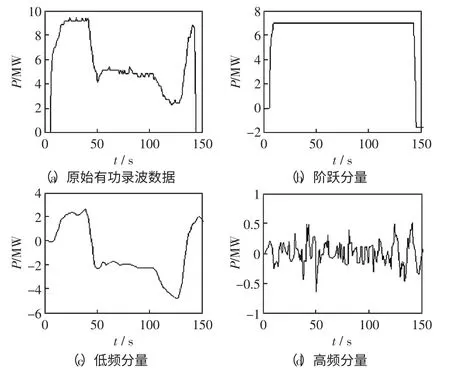
图6 单列机车时牵引负荷有功功率分解Fig.6 Active power decomposition of single electric locomotive
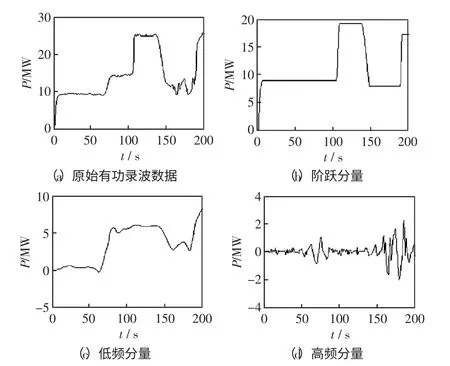
图7 多列机车交汇时牵引负荷有功功率分解Fig.7 Active power decomposition with multiple electric locomotives intersection
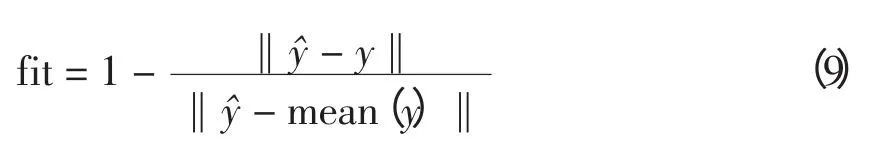
式中:y 为实测数据;y为拟合数据。一致性系数越大,拟合效果越好。
低频缓坡分量的ARMA 模型采用不同的阶数时,一致性系数如表1 所示。由表1 可知,当pl=2,ql=1 时,低频缓坡分量的拟合效果已较好,此时提高ARMA 模型的阶数,对拟合的效果并没有明显改善。为了简化ARMA 模型,应尽量降低其阶数。经多次应用,归纳出低频缓坡分量ARMA 模型阶数的经验值为pl=2,ql=1。同理,归纳出高频随机分量ARMA 模型阶数的经验值为ph=4,qh=6。
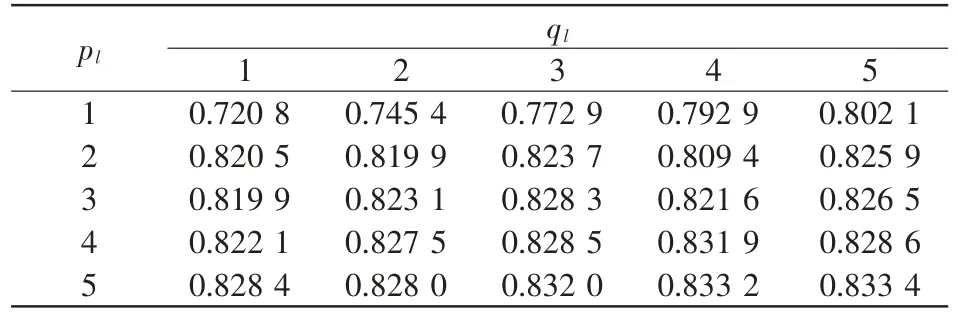
表1 不同阶数低频分量模型的一致性系数Tab.1 Coefficients of consistency with different orders
确定模型阶数后,采用5 步向前预测的ARMA 模型,即可得到t 时刻向前5 步的预测值。
对拟合后的3 类分量进行合成即可得到牵引负荷有功功率最终的拟合值,并与直接采用ARMA 模型进行拟合的方法对比,如图8 所示。
定义绝对平均误差MAD(mean absolute deviation)为


图8 牵引负荷有功功率拟合曲线Fig.8 Fitting curves of active power for traction load
均方差MSE(mean squared error)为
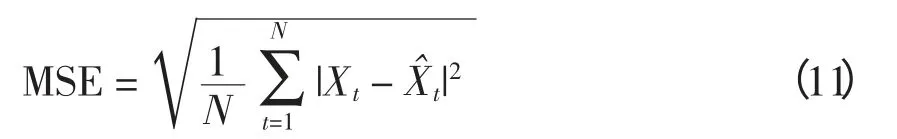
不同拟合方法的误差如表2 所示。由图8 和表2 可知,采用本文提出的牵引负荷功率模型拟合方法所得的曲线与牵引变实测功率曲线基本重合,误差明显小于直接采用ARMA 模型拟合的方法,可认为该方法是准确有效的。
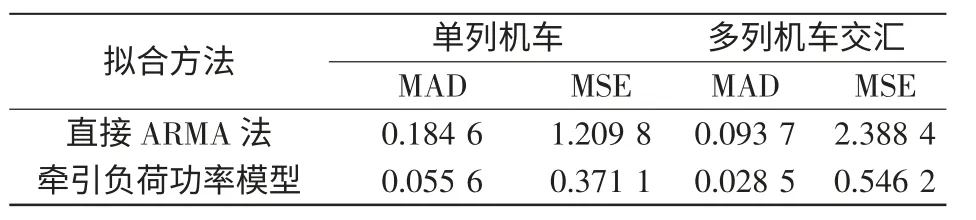
表2 不同拟合方法误差对比Tab.2 Errors with different methods
5 结语
电铁牵引负荷具有较强的随机波动性和冲击性,其波动可分为阶跃型波动、低频缓坡型波动及高频随机波动。鉴于此,基于波形分解与小波变换,将牵引变的功率波动分解为阶跃分量、低频缓坡分量与高频随机分量,建立一种基于时间序列功率模型。现场数据应用结果表明,该方法明显优于直接ARMA 法,能很好地拟合实际功率波动曲线。电铁牵引负荷功率模型能反映牵引负荷的随机波动性与冲击性,可应用于电力系统分析软件中,分析其对局部电网及机组功率振荡的影响。
[1]韩宝明.高速铁路概论[M].北京:北京交通大学出版社,2008.
[2]李琼林,刘书铭,余晓鹏,等(Li Qionglin,Liu Shuming,Yu Xiaopeng,et al). 300 km/h 系列高速客运专线对电网电能质量的影响研究(Study on the impact of the 300 km/h series high-speed special railway on the grid power quality)[J].电力系统保护与控制(Power System Protection and Control),2011,39(22):78-82,89.
[3]于坤山,周胜军,王同勋,等.电气化铁路供电与电能质量[M].北京:中国电力出版社,2010.
[4]Dai N Y,Lao K W,Wong M C,et al.Hybrid power quality conditioner for co-phase power supply system in electrified railway[J].IET Power Electronics,2012,5(7):1084-1094.
[5]Pee-Chin Tan,Poh Chiang Loh,Holmes D G. Optimal impedance termination of 25 kV electrified railway systems for improved power quality[J]. IEEE Trans on Power Delivery,2005,20(2):1703-1710.
[6]Battistelli L,Lauria D,Proto D.Two-phase controlled compensator for alternating -current quality improvement of electrified railway systems[J]. IEE Proceedings-Electric Power Applications,2006,153(2):177-183.
[7]李欣然,张广东,朱湘有,等(Li Xinran,Zhang Guangdong,Zhu Xiangyou,et al). 牵引供电系统综合负荷模型结构(A load model of traction power supply system)[J].电力系统自动化(Automation of Electric Power Systems),2009,33(16):71-75,95.
[8]张永旺,李欣然,李金鑫,等(Zhang Yongwang,Li Xinran,Li Jinxin,et al).牵引供电系统综合负荷实测建模(Measurement-based composite load modeling of traction power supply system)[J]. 电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(1):94-99.
[9]张睿,蔡国伟,陈兴雷,等(Zhang Rui,Cai Guowei,Chen Xinglei,et al).基于等效变换的牵引负荷建模(A traction load modeling method based on equivalent transformation)[J].中国电力(Electric Power),2012,45(1):15-19,32.
[10]鞠平,秦川,黄桦,等(Ju Ping,Qin Chuan,Huang Hua,et al).面向智能电网的建模研究展望(Research trends of power system modeling geared to smart grid)[J].电力系统自动化(Automation of Electric Power Systems),2012,36(11):1-6.
[11]杨国清,姚李孝,熊峰(Yang Guoqing,Yao Lixiao,Xiong Feng).交流传动牵引负荷冲击特性研究(Research on the shock characteristics of ac drive traction loads)[J]. 西安理工大学学报(Journal of Xi′an University of Technology),2013,29(1):103-108.
[12]Ho T K,Chi Y L,Wang J,et al. Probabilistic load flow in AC electrified railways[J]. IEE Proceedings-Electric Power Applications,2005,152(4):1003-1013.
[13]杨少兵,吴命利(Yang Shaobing,Wu Mingli).电气化铁道牵引变电所负荷概率模型(A load probability model for electrified railway traction substations)[J].电力系统自动化(Automation of Electric Power Systems),2010,34(24):40-45.
[14]李群湛,连级三,高仕斌.高速铁路电气化工程[M].成都:西南交通大学出版社,2006.
[15]鞠平,王耀,项丽,等(Ju Ping,Wang Yao,Xiang Li,et al).考虑特殊负荷的宁夏电网负荷建模(Load modeling for Ningxia grid with special loads)[J]. 电力自动化设备(Electric Power Automation Equipment),2012,32(8):1-4,21.
[16]夏冬,吴俊勇,贺电,等(Xia Dong,Wu Junyong,He Dian,et al).一种新型的风电功率预测综合模型(A novel combined model for wind power forecasting based on maximum entropy principle)[J]. 电工技术学报(Transactions of China Electrotechnical Society),2011,26(S1):262-266.
[17]王波,邰能灵,翟海青,等(Wang Bo,Tai Nengling,Zhai Haiqing,et al).基于混合粒子群算法的短期负荷预测模型(Hybrid optimization method based on evolutionary algorithm and particle swarm optimization for short-term load forecasting)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2008,20(3):50-55.
[18]贺仁睦,叶静,范瑞祥(He Renmu,Ye Jing,Fan Ruixiang).对牵引负荷实测数据的选取与分析(The selection of measuring data for traction load and its analysis)[J].现代电力(Modern Electric Power),2012,29(2):17-21.
[19]周厚奎,张昱,金心宇(Zhou Houkui,Zhang Yu,Jin Xinyu).基于傅里叶和小波变换的电网谐波分析(Power harmonic analysis based on Fourier and wavelet transform)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2005,17(6):59-62,99.
[20]王丽婕,冬雷,廖晓钟,等(Wang Lijie,Dong Lei,Liao Xiaozhong,et al).基于小波分析的风电场短期发电功率预测(Short-term power prediction of a wind farm based on wavelet analysis)[J].中国电机工程学报(Proceedings of the CSEE),2009,29(28):30-33.

