温控负荷直接负荷控制策略与优化调度
邓宇鑫,王 磊,李 扬,田 杰
(1.东南大学电气工程学院,南京210096;2.深圳供电局有限公司,深圳518048)
直接负荷控制DLC(direct load control)是一种重要的激励型需求响应DR(demand response)技术,其实施对象为居民或小型商业用户中的空调等具有热能储存能力的温控负荷TCL(thermostatically controlled loads)[1]。理论研究及应用实践结果表明,DLC 能够有效地降低系统高峰负荷,提高负荷率,充分利用需求侧资源,对提高电力系统安全经济运行有积极作用[2]。
DLC 在国外已实施多年,文献[3-5]分别介绍了澳大利亚和美国的DLC 项目实施情况,不少学者对DLC 进行了研究,文献[6-8]采用动态规划方法求解DLC 问题,其中文献[6]以系统最大负荷最小化或运行成本最小化为目标,文献[7]将DLC 调度模型和机组组合模型结合,文献[8]增加了对用户舒适度,负荷预测误差等的考虑。文献[9]以系统最大负荷最小化为目标构建了线性规划DLC 模型,并提出全时段、单时段、两时段3 种控制策略。文献[10-11]分别使用带精英策略的非支配排序遗传算法NSGA-Ⅱ(non dominated sorting genetic algorithmⅡ) 和迭代深化遗传算法IDGA(iterative deepening genetic al-gorithm)求解DLC 问题。上述文献通常对温控负荷作一旦开启便保持额定功率运行的假设,以延迟负荷模型[6],阶段性补偿模型[7-8,10-11]或固定的能量补偿模式[9]等简化模型描述DLC 结束后的反弹负荷,这些简化与温控负荷实际运行状况存在不小的差异。为使DLC 的实施结果更加可靠准确,文献[12-14]着眼于对温控负荷进行精细化建模并提出了物理负荷模型,试验结果表明,物理负荷模型能够准确描述温控负荷的运行状态。
本文采用物理负荷模型描述温控负荷,采用蒙特卡洛模拟方法在模型参数取值区间内抽样获取用户群归一化因子,考虑DLC 实施期间的用户自主退出和设备故障,分析了DLC 控制策略原理并提出DLC 优化调度模型,算例分析表明该模型能达到满意的结果。
1 温控负荷物理模型
温控负荷是DLC 的主要实施对象,考虑温控负荷自身功率、环境温度、房间热力学参数等,表征温控负荷的运行状态[12]为
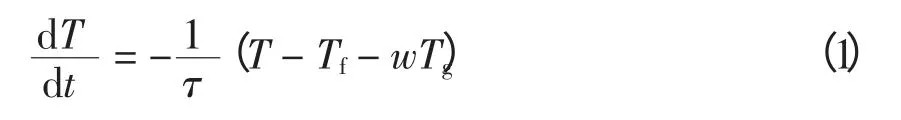
式中:T 为温控器测得的室内温度;w 为温控负荷的运行/停止状态,运行时为1,停止时为0;τ 为房屋热时间常数;Tf为无温控负荷时的室内温度,可被近似认为等于室外环境温度;Tg为温控负荷的温度增益。
以h 为间隔将时间t 离散化,假设温控负荷的运行/停止状态的变化是在前一个时段结束和下一个时段开始的临界点进行,并引入高斯白噪声V(nh)以计及开关窗户和室内人员活动等其他随机因素对房间温度影响[15],由式(1)可得
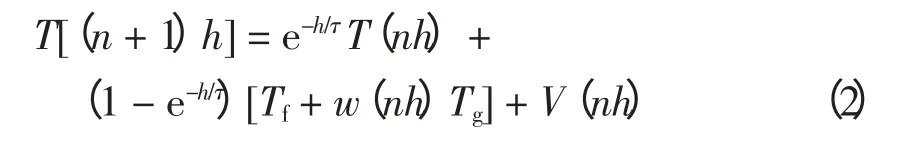
若温控负荷用于制冷,则温控负荷的运行/停止状态[16]服从
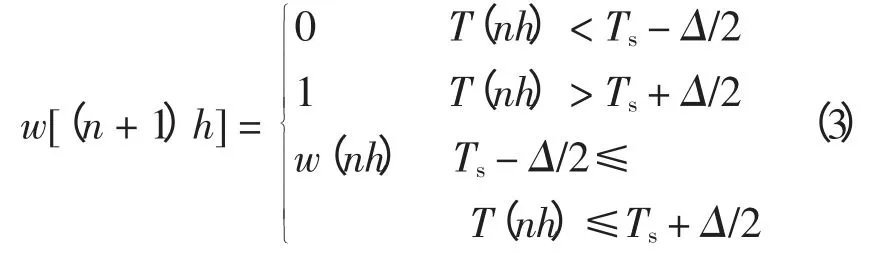
式中:Ts为温控负荷温度设定值;Δ/2 为温控器动作的温度阈值。
式(2)~(3)描述了一个单独温控负荷的运行状况,对有大量的温控负荷参与的DLC 项目,通过对温控负荷参数进行调查确定τ、Ts、Tg、Δ 所服从的概率分布后,可在单个温控负荷物理模型的基础上采用蒙特卡洛模拟方法在上述参数取值区间内进行抽样。定义时段nh 的归一化因子[16]为
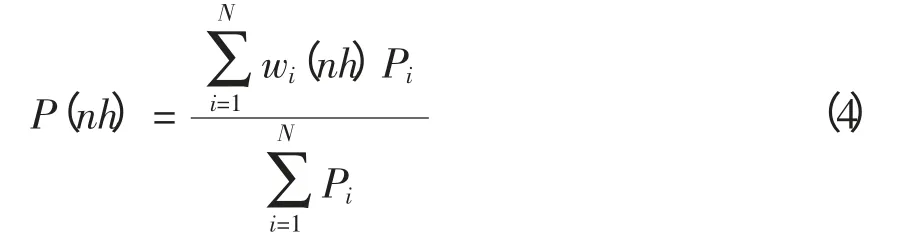
式中:wi(nh)为在时段nh 第i 个温控负荷运行状态量;Pi为第i 个温控负荷的额定功率;N 为抽样的温控负荷总数。归一化因子能够反映温控负荷群各时段的实际负荷值占额定负荷值的比例。
结合温控负荷物理模型和核光滑估计技术可以计算参加DLC 的用户室温概率密度分布。通过蒙特卡洛模拟得到N 个用户的室内温度yi(t)(i=1,…,N),则在t=nh,用户的室温概率密度函数可利用核光滑估计公式[17]计算,即
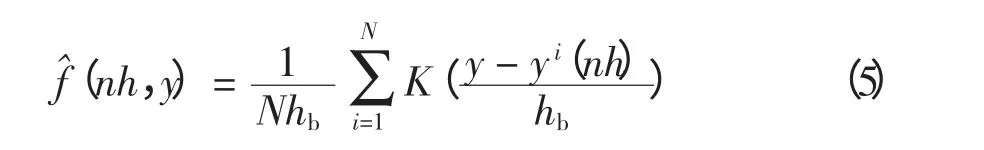
式中:K 为核的类型,常用的有高斯核和三角核等,本文采用高斯核;hb为带宽,可证明高斯核的最优带宽[18]为
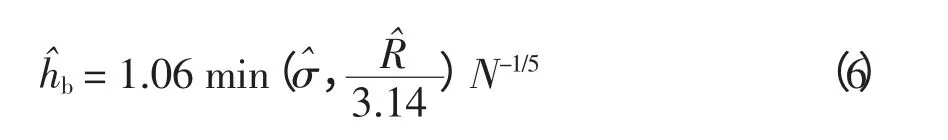
2 DLC 控制策略
对制冷空调负荷而言,DLC 控制手段一般有以下3 种:①关闭空调;②对空调进行占空比控制;③提升空调温度设定值[10]。关闭空调是最简单的DLC 控制手段,本文不做过多讨论。
2.1 提升温度设定值
由式(1),令T(t)|t=0=Ts+Δ/2,对单台空调有如下情形。
情形1 Tf〈Ts+Δ/2 时,空调将不会运行;
情形2 Ts+Δ/2〈Tf〈Ts-Δ/2-Tg时,空调能把室内温度降低到Ts-Δ/2,空调将间歇运行,其运行时间ton和停止时间toff分别为
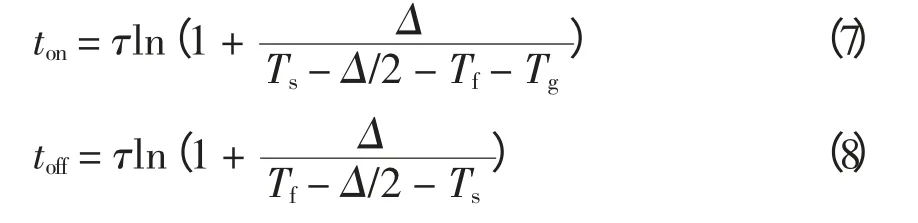
情形3 Ts-Δ/2-Tg〈Tf〈Ts+Δ/2-Tg时,空调只能把室内温度降低到Tf+Tg而无法降低到Ts-Δ/2,空调将持续运行;
情形4 Tf〉Ts+Δ/2-Tg时,即使空调运行室内温度也无法下降,空调将持续运行。
由情形2 可知,当室外温度不是太低或太高时,提升温度设定值将使ton变小,toff变大,从而使空调的平均功率降低。由情形1、3、4 可知,当室外温度过低或过高时,提升温度设定值后负荷削减量将较小,因为温度过低时大部分空调不会运行,温度过高时部分空调因制冷能力不足受控后仍会持续运行。由上述分析可知提升温度设定值宜与其他控制手段配合使用。
2.2 占空比控制
对空调进行占空比控制是实际DLC 项目广泛采用的控制策略。实际上空调开启后并非一直处于运行状态,而是处于不断运行/停止的循环之中,其运行占空比(duty cycle)等于一定时间内实际运行时间与总时间之比,表示为

以P(t)代表空调实时功率,空调运行时其为额定功率P,停止时为0,则平均功率Pave为
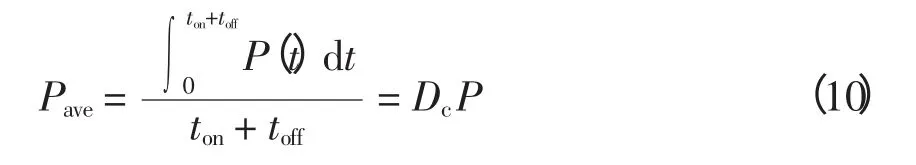
若强制让用户空调的运行占空比低于其未受控时的自然占空比(natural duty cycle),便可达到削减负荷的目的。目前使用较多的有50%、66%等占空比控制策略,分别是对空调进行15min/15min和20min/10min 开启关闭控制,其负荷削减值最大将分别达到额定空调负荷的50%和33%。
2.3 DLC 控制方案
根据前文所述的3 种DLC 控制手段,结合实际项目的运行经验可设计A、B、C 3 种控制方案,如表1 所示。参与DLC 的用户可视自身情况申报其中一种DLC 控制方案,DLC 合同亦规定用户参与DLC 事件的总次数,当被调用次数超过总次数后将不再被控。在具体执行时每类控制方案可细分为多种控制策略[19],通过3 种方案的配合可以在DLC 事件执行时完成DLC 实施方给定的负荷削减需求。

表1 DLC 控制方案Tab.1 DLC control scheme
3 DLC 优化调度
3.1 控制策略评估
由温控负荷物理模型,假设第m 类控制方案中第n 种控制策略为从时段a 至时段b 采用控制手段k 进行控制,则用户数量为Nj的第j 组用户接受该控制策略时在时段t 的负荷Pj,m,k,a,b,t为
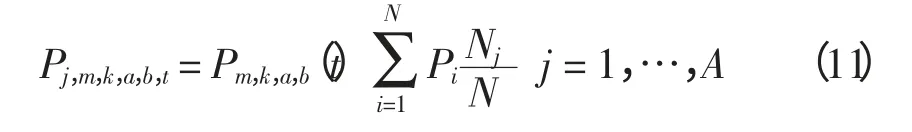
式中:Pm,k,a,b(t)为接受第m 类控制方案中从时段a至时段b 采用控制手段k 进行控制后在时段t 的归一化因子;A 为总的用户组数。
3.2 用户自主退出和设备故障的影响
在DLC 事件执行过程中允许用户自主退出受控(override)对DLC 项目的成功实施非常重要,它能有效消除用户对参与DLC 后便失去自主控制权的顾虑,大幅提高DLC 项目的参与度和用户满意度,目前绝大多数实际运行的DLC 项目都允许用户自主退出受控[5,20-21]。同时,DLC 执行过程中会存在一些用户由于控制设备或通信设备故障而未能参与受控。考虑用户自主退出和设备故障后DLC控制策略的结果将出现变化,当用户数量为Nj的第j 组用户接受第m 类控制方案中从时段a 至时段b 采用控制手段k 进行控制时,其在时段t 的修正负荷P′j,m,k,a,b,t可表示为
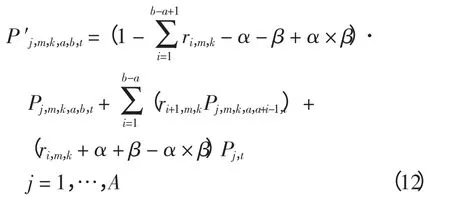
式中:α 和β 分别为控制设备和通信设备故障率;ri,m,k为接受第m 类控制方案中控制手段k 后用户在DLC 开始执行后第i 时段初的自主退出率,可由历史统计数据得出;Pj,t为第j 组用户未接受DLC 时在时段t 的负荷。式(12)右端3 项分别代表DLC执行过程中未选择自主退出、选择自主退出和未参与DLC 的用户负荷。
3.3 DLC 优化调度模型
3.3.1 目标函数
目标函数1 实施DLC 的首要目标是执行DLC 时各时段的实际负荷削减值与负荷削减需求的偏差最小,即
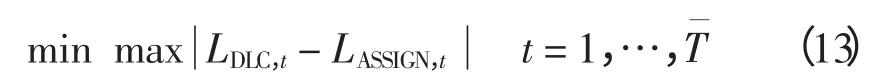
式中,LDLC,t为通过DLC 在第t 时段削减的负荷。
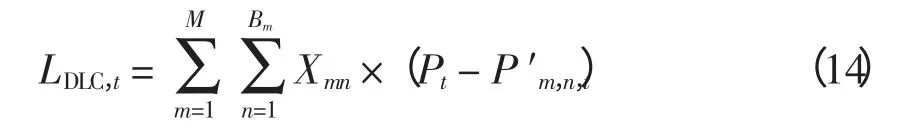
式中:Pt为未参与DLC 时每组用户在时段t 的负荷,本文考虑对参与DLC 的用户进行平均分组的模式;P′m,n,t为采用第m 类控制方案中第n 种控制策略时每组用户在时段t 的修正负荷;LASSIGN,t为t时段的削减需求;T¯为总时段数;Xmn为整型决策变量,代表采用第m 类控制方案中第n 种控制策略的用户总组数;M 和Bm为分别代表控制方案类别总数,每种控制方案类别对应的控制策略总数。
参与DLC 的设备在受控结束后产生的比未参与DLC 时更大的负荷被称为反弹负荷,若较大的反弹负荷和较大系统负荷共存则会产生2 次高峰负荷,因此在模型中必须计及抑制反弹负荷的目标。定义DLC 模式1 为:负荷削减需求结束后所有用户退出受控;DLC 模式2 为:负荷削减需求结束后允许用户在一定时间内继续受控。由于模式2中用户在负荷削减需求结束后可逐步退出受控,其产生的反弹负荷峰值将小于模式1。
目标函数2 本文基于模式2 在优化模型中加入目标函数2,在负荷削减需求结束后,DLC 产生的反弹负荷应尽可能小,即
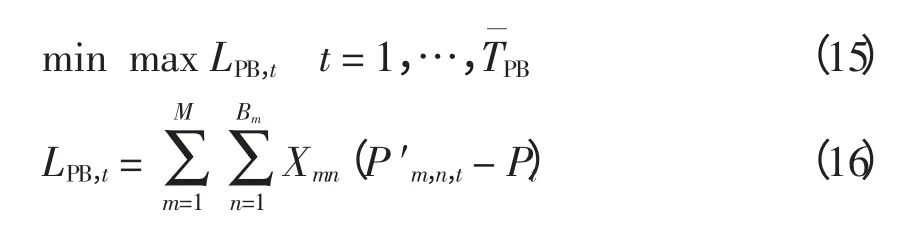
式中:LPB,t为DLC 结束后在第t 时段产生的反弹负荷;为在负荷削减需求结束后考虑反弹负荷的时段数。
3.3.2 约束条件
1)可调资源总量约束
DLC 合同规定了用户参与DLC 事件的最大次数,执行DLC 时每类控制方案的实际受控用户组数不小于0,且不超过申报参与该类方案的尚能够参与受控的总用户组数:
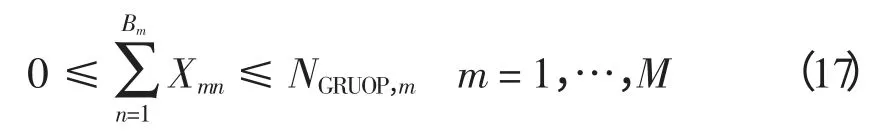
式中,NGRUOP,m为申报参与第m 类控制方案且还能参与受控的用户组数。
2)受控用户组数非负
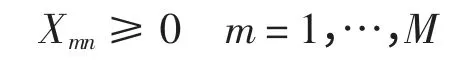

3)受控用户组数为整数
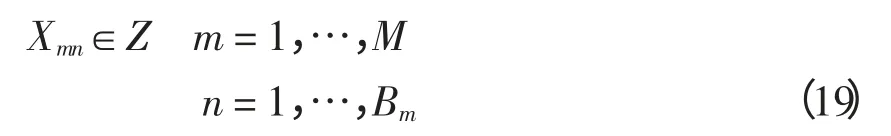
4)反弹时段约束
在负荷削减需求结束后允许用户继续受控的时段范围内,反弹负荷必将开始出现

事实上,由于DLC 控制策略是有限的,DLC执行时的实际负荷削减与负荷削减需求之间必将有误差,因此可将目标函数1 写成模糊形式为
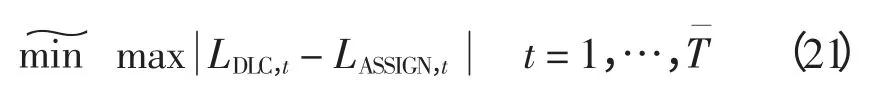
定义
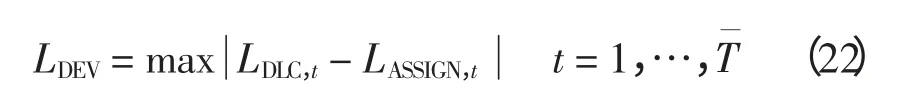
对目标函数1 建立隶属度函数为

式中,b1和q1由DLC 实施方指定。
由于负荷削减需求的存在使得反弹负荷必将出现,DLC 实施方通常只希望反弹负荷小于一定水平即可,因此可将目标函数2 写成模糊形式为
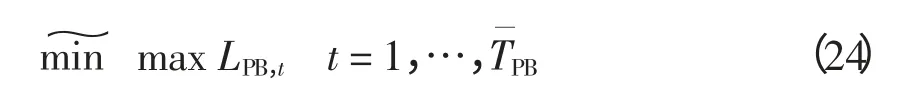
定义
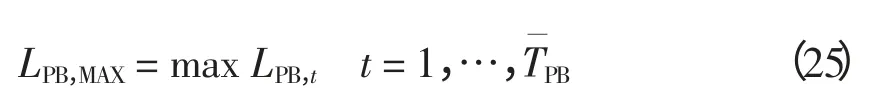
对目标函数2 建立隶属度函数为
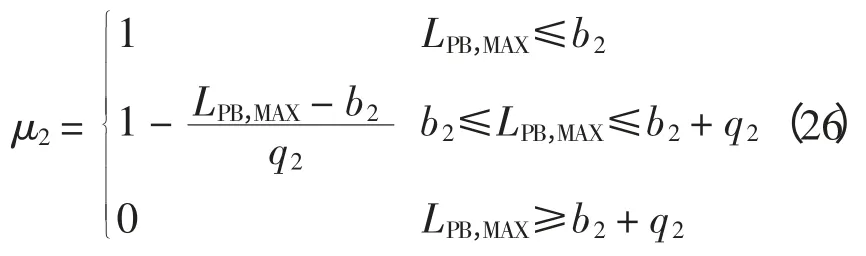
式中,b2和q2由DLC 实施方指定。
根据模糊多目标决策中的扩展极大极小法[22],DLC 优化调度模型可写为
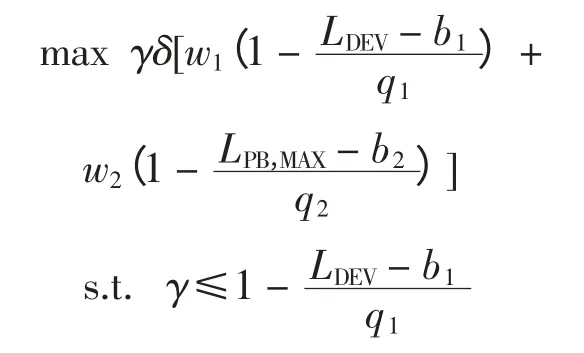
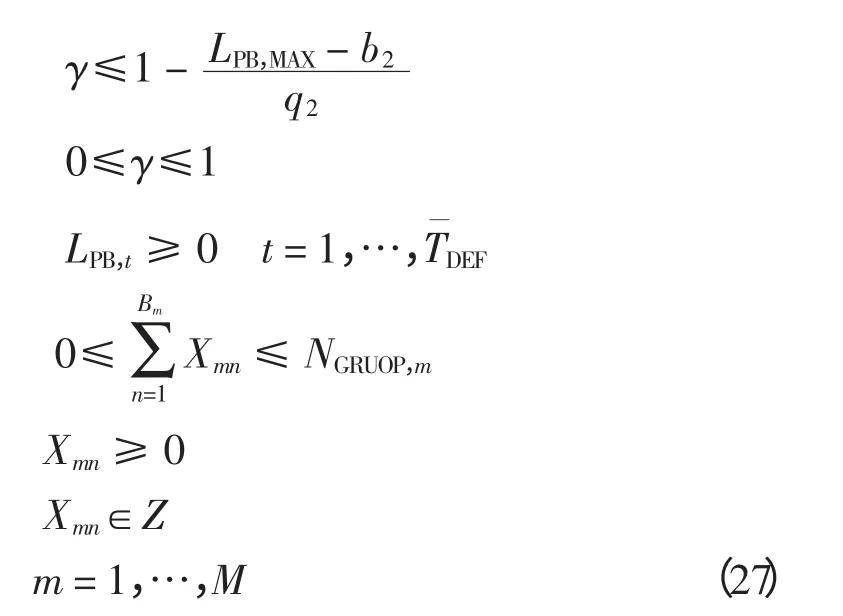
式中:γ 为辅助变量;δ 为充分小正数;w1和w2分别为目标1 和目标2 的权重。
4 算例分析
假设某DLC 项目有40 000 户用户参与,以1 000 户用户为一组,其中第1~10 组,第11~25组,第26~40 组用户分别申报参与了A 类、B 类和C 类控制方案。根据调查数据,用户参数服从正态分布,其均值和标准差如表2 所示[23]。

表2 用户参数Tab.2 Parameters of DLC participants
以30 min 为一个时段,DLC 实施方要求某日在14:00—19:00(时段29~38)持续削减负荷7 500 kW。b1、q1、b2、q2、w1、w2的取值分别被DLC 实施方指定为200 kW、800 kW、2 500 kW、5 000 kW、0.5、0.5。室外温度数据如图1 所示,各种控制手段的用户自主退出率历史统计值如图2 所示,控制设备故障率为0.5%,通信设备故障率为0.5%。使用Matlab2011b 编程,采用CPLEX 12.4 求解优化调度模型。
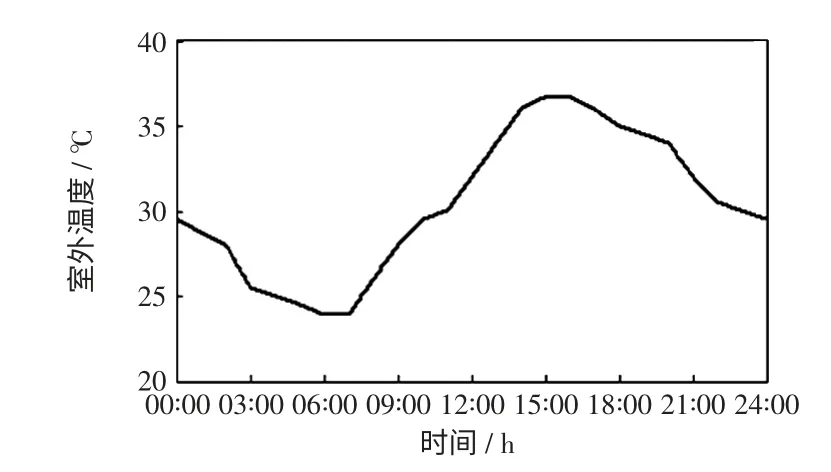
图1 室外温度Fig.1 Outdoor temperature
4.1 DLC 优化调度结果
应用本文提出的DLC 优化调度模型,各组用户的受控手段和受控时段如表3 和图3 所示。
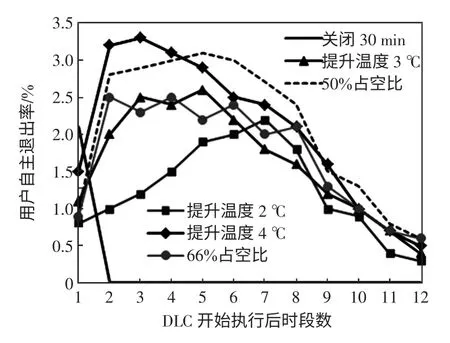
图2 各种控制手段的用户自主退出率Fig.2 Override rate of various control methods

表3 优化调度结果Tab.3 Result of optimal scheduling
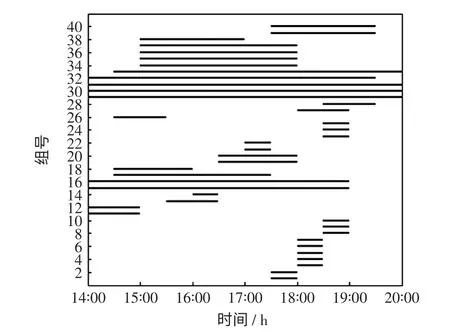
图3 各组用户受控时段Fig.3 Controlled period of DLC participants
4.2 负荷削减效果分析
DLC 前后的空调负荷如图4 所示,本文所提模型在给定的时段29~38 内达到了负荷削减要求,同时由于第28~33 组和第39~40 组用户在负荷削减需求结束后继续受控并最终在19:30(时段39 末)或20:00(时段40 末)退出,反弹负荷峰值与DLC 模式1 相比明显降低。
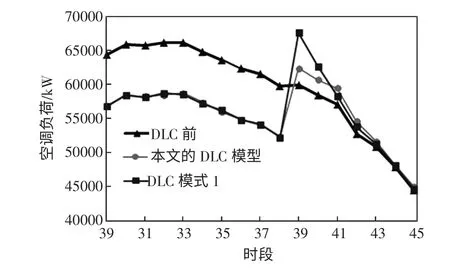
图4 DLC 前后的空调负荷Fig.4 Demand of air conditioning before and after DLC
选取第1、15、32 组用户为例研究A、B、C 3 类控制方案的负荷削减特性,如图5~图7 所示。当不考虑用户自主退出和设备故障时,第1 组用户在时段36 关闭空调30 min,其受控时段的负荷削减值最大;第15 组用户在时段29~38 提升空调温度设定值4 ℃,其负荷削减在刚受控时很大,之后在经历一个衰减后保持在较为恒定的水平;第32 组用户在时段29~39 进行50%占空比控制,其负荷削减值总体平稳并呈下降趋势。受控结束后的反弹负荷持续时间一般不超过6 个时段。当考虑用户自主退出和设备故障后,DLC 负荷削减结果将出现变化,由图5~图7 可知,第1 组用户由于只受控1 个时段故变化较小,而对第15 和32 组用户而言,与未考虑用户自主退出和设备故障时相比,各时段负荷削减量的减少值分别在DLC 执行的前9 个和前10 个时段随时间的增加呈增大趋势,而在第10 个和第11 个时段又分别有所下降,其负荷削减量减少百分比的最大值已接近30%,当DLC 执行结束后,反弹负荷值也将出现变化。由于用户自主退出和设备故障会对DLC 控制策略结果产生影响,在DLC 调度中必须对其予以考虑。
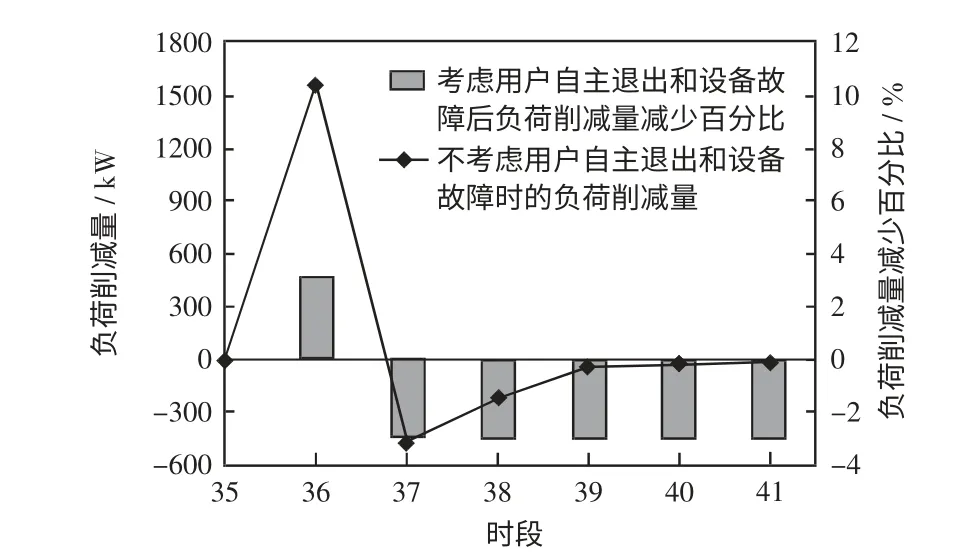
图5 第1 组用户削减负荷Fig.5 Load reduction of DLC participants group 1
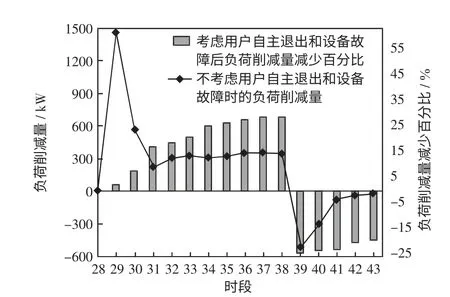
图6 第15 组用户削减负荷Fig.6 Load reduction of DLC participants group 15
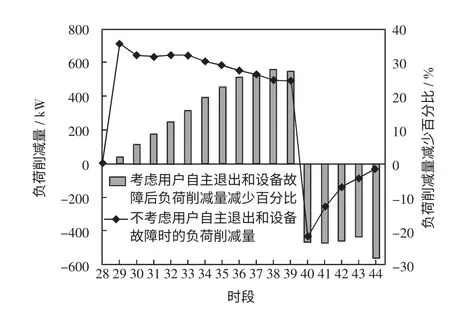
图7 第32 组用户削减负荷Fig.7 Load reduction of DLC participants group 32
4.3 用户舒适度影响分析
本次DLC 执行总时间为6 h,选取DLC 开始后1 h、3 h、5.5 h 研究DLC 执行过程中用户舒适度所受影响。图8 所示是执行和未执行DLC 时所有用户在对应时刻的室内温度概率密度函数,舒适度受到影响的用户在DLC 执行1 h 后仍较少,DLC执行3 h 后增多,DLC 执行5.5 h 后重归于较少。根据ASHRAE 推荐的夏季热舒适温度上限26 ℃,从整体上看,DLC 执行过程中舒适度受到较大影响的用户比例是较小的。
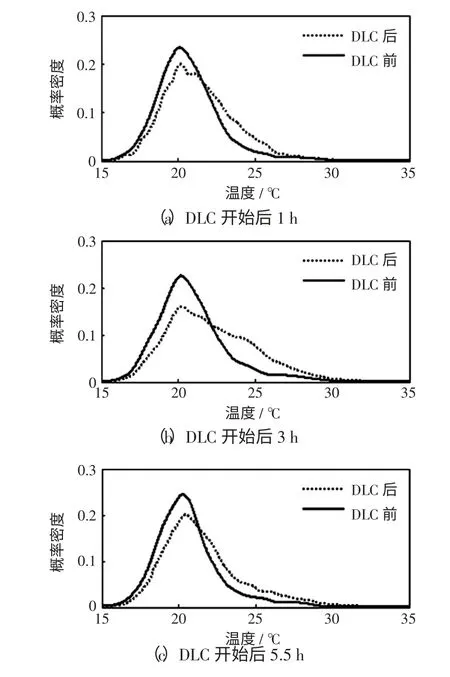
图8 DLC 对所有用户室内温度的影响Fig.8 Impact on indoor temperature of all DLC program participants
5 结语
本文利用物理负荷模型描述温控负荷,考虑DLC 实施期间的用户自主退出和设备故障,基于实用的控制手段提出了DLC 优化调度模型,算例分析验证了所提模型的可行性和实用性。智能电网技术的发展[24]和温控负荷的不断增加使DLC 削减负荷的潜力不断增大,而DLC 带来的利益体现在多个方面:推迟新增发电机组的投资,减少机组运行成本,提高电力系统可靠性,帮助电力公司规避批发市场的高峰电价、节能减排等。综合考虑DLC的利益并从长期资源规划的角度研究DLC 项目的补偿机制是一个值得深入研究的课题,也是本文下一步的研究方向。
[1]张钦,王锡凡,王建学,等(Zhang Qin,Wang Xifan,Wang Jianxue,et al).电力市场下需求响应研究综述(Survey of demand response research in deregulated electricity markets)[J]. 电力系统自动化(Automation of Electric Power Systems),2008,32(3):97-106.
[2]唐为民,王蓓蓓,施伟(Tang Weimin,Wang Beibei,Shi Wei). 基于模糊动态规划的直接负荷控制策略研究(The strategy research of direct load control based on fuzzy dynamic program)[J].中国电力(Electric Power),2003,36(8):24-28.
[3]Khanna I. Smart Grid Application:Peak demand management trial-the Western Australian experience[C]//IEEE PES Innovative Smart Grid Technologies,Perth,Australia,2011.
[4]Anon. ETSA utilities air conditioner direct load control program-Australia [EB/OL]. http://www.ieadsm.org/Files/Content/ETSA%20Utilities_2009-05-28.pdf,2009.
[5]Anon. LIPAEDGE direct load control program-USA[EB/OL].http://www.ieadsm.org/Files/Content/LIPAedge_2011-03-16.pdf,2011.
[6]Cohen A I,Wang C C. An optimization method for load management scheduling[J]. IEEE Trans on Power Systems,1988,3(2):612-618.
[7]Hsu Yuan-Yih,Su Chung-Ching. Dispatch of direct load control using dynamic programming[J].IEEE Trans on Power Systems,1991,6(3):1056-1061.
[8]Huang K Y,Yang H T,Liao C C,et al.Fuzzy dynamic programming for robust direct load control[J].Energy Management and Power Delivery,1998,2:564-569.
[9]Kurucz C N,Brandt D,Sim S.A linear programming model for reducing peak through customer load control programs[J].IEEETransonPowerSystems,1996,11(4):1817-1824.
[10]张钦,王锡凡,别朝红,等(Zhang Qin,Wang Xifan,Bie Zhaohong,et al). 电力市场下直接负荷控制决策模型(A decision model of direct load control in electricity markets)[J].电力系统自动化,2010,34(9):23-28.
[11]Yao Leehter,Chang Wen-Chi,Yen Rong-Liang. An iterative deepening genetic algorithm for scheduling of direct load control[J]. IEEE Trans on Power Systems,2005,20(3):1414-1421.
[12]Ihara S,Schweppe F C. Physically based modeling of cold load pickup[J]. IEEE Trans on Power Apparatus and Systems,1981,100(9):4142-4150.
[13]Pahwa A,Brice C W.Modeling and system identification of residential air conditioning load[J].IEEE Trans on Power Apparatus and Systems,1985,104(6):1418-1425.
[14]Molina A,Gabaldon A,Fuentes J A,et al. Implementation and assessment of physically based electrical load models:application to direct load control residential programmes[J].IEE Proceedings-Generation,Transmission and Distribution,2003,150(1):61-66.
[15]Mortensen R E,Haggerty K P.A stochastic computer model for heating and cooling loads[J]. IEEE Trans on Power Systems,1988,3(3):1213-1219.
[16]Ucak C,Caglar R.The effects of load parameter dispersion and direct load control actions on aggregated load [C]//International Conference on Power System Technology. Beijing,China,1998:280-284.
[17]Mo1ina-Garcia A,Kessler M,Fuentes J A,et al. Probabilistic characterization of thermostatically controlled loads to model the impact of demand response programs[J].IEEE Trans on Power Systems,2011,26(1):241-251.
[18]W Hardle.Smoothing Techniques[M].New York:Springer-Verlag,1991.
[19]Ruiz N,Cobelo I,Oyarzabal J.A direct load control model for virtual power plant management[J]. IEEE Trans on Power Systems,2009,24(2):959-966.
[20]Weller,G H.Review of Current Southern California Edison Load Management Programs and Proposal for a New Market-Driven,Mass-Market,Demand-Response Program[R].Berkeley:Lawrence Berkeley National Labortory,2002.
[21]Goldman C,Reid M,Levy R,et al. Coordination of energy efficiency and demand response[R]. Berkeley:Lawrence Berkeley National Labortory,2010.
[22]Lai Young-Jou,Hwang Ching-Lai.Possibilistic linear programming for managing interest rate risk[J].Fuzzy Sets and Systems,1993,54(2):135-146.
[23]Ucak C,Dokuyucu G. Investigation of thermostat-set control as a new direct load control method [C]//Second International Conference on Electrical and Electronics Engineering,Bursa,Turkey,2001.
[24]孔祥玉,赵帅,贾宏杰,等(Kong Xiangyu,Zhao Shuai,Jia Hongjie,et al).智能电网中电力设备及其技术发展分析(Analysis of equipment and technology in smart grid development)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2012,24(2):21-26.

