配电网重构的拓扑结构快速适应法
费汪浩,武晓朦,张杰英,封 园,杨 阳,2
(1.西安石油大学电子工程学院,西安710065;2.延长油田股份有限公司子北采油厂,延安717300)
配电网潮流计算与拓扑结构分析是研究配电网自动化高级应用功能的基础,也是配电网重构的必要方法之一。配电网的网络结构与输电网存在极大不同,一般采用闭环设计,辐射状运行。且配电网存在R/X 比值较大等特点[1],使得针对输电网的潮流计算必然与配电网存在明显差异,经典潮流算法不能良好的应用于配电网。目前针对配电网潮流计算的文献较多[2-5],但大多算法仍然离不开前推回代算法的框架。采用该算法在形成配电网邻接矩阵的过程中,已经人为的规定了潮流方向,而配电网重构将改变网络拓扑结构,潮流方向必然发生变化,且采用邻接矩阵存在占用空间大、计算时间长等缺点。因此,急需提出一种消耗内存小,计算速度快,且能够快速适应配电网拓扑结构变化的计算方法。
为解决这一问题,文献[6]采用自定义的层次矩阵,能够根据配电网拓扑结构的变化自动更新赋值;文献[7]采用邻接表直观地表示了配电网的拓扑结构,并给出了拓扑结构改变后邻接表更新和潮流计算方法。这些方法在一定条件下实现了配电网重构后的潮流计算。
本文在上述文献的基础上提出一种拓扑结构快速适应的配电网重构方法。将网络划分为支链形式,利用深度优先遍历DFS(depth first search)的编号特点和图论中顶点出度的定义,确定支链邻接表。利用支链的特点,快速适应组环和解环带来的拓扑结构的变化,并确定解环后的支链邻接表及其前推回代方向。
1 配电网拓扑结构分析
1.1 配电网支链划分方法
配电网分支多,干线长,且网架结构上存在较多复杂的网络元件,如果直接对其拓扑结构进行分析,难度较大,需采用简化方法。文献[8]将配电网表示成一个图结构G,其中,开关等效为图的边e,开关间的馈线、负荷和配变等结构单元等效为图的顶点v。
正常情况下,配电网呈辐射状开环运行的树状结构,该结构中,任意2 顶点之间的路径唯一且具有方向性(潮流方向)。因此,任意2 节点vj、vk之间的映射关系ψ 唯一确定,记为

式中:ej,k为vj、vk两节点之间的边串联形成的连通路径,该连通路径唯一;vs为连通路径上的某节点,该路径方向从vj指向vk。特别是当vj与vk相邻时,其映射关系记为

文献[7]认为每条馈线的潮流分布与其他馈线相独立,潮流计算时可并行计算。然而,如果固定图结构中的根节点为源点,另任取2 节点,分别按式(1)做出映射,则由此形成的2 条映射关系可能会存在重叠交替的情况。为避免映射重叠,需对式(1)的节点位置加以约束。
将配电网辐射状运行时的网架结构划分成n段支链,且每条支链均不存在分支。则式(1)映射关系为
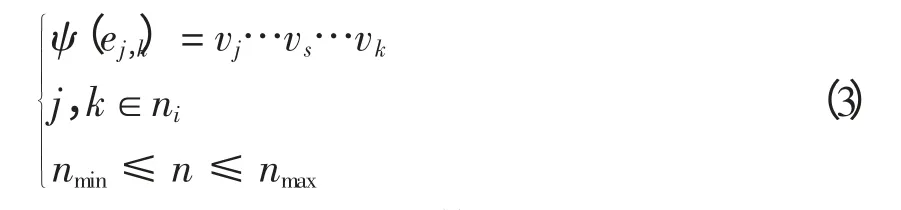
式中,i 为支链编号。按式(3)划分出的配电网最小单元为相邻负荷节点间的连通关系,此时,支链个数n 等于配电网支路个数nmax。而当n 取nmin时,按图论中顶点“出度”的定义:配电网辐射状结构中,除末端节点外的所有节点出度O(vi)大于等于1。对于任意支链,其末端节点出度均不为1,而根节点所在支链首端节点的出度由网架结构决定,其余每条支链首端节点的出度均大于1。按出度划分的支链个数等于网架中根节点出度和其余所有出度大于1 的节点的出度相加,即
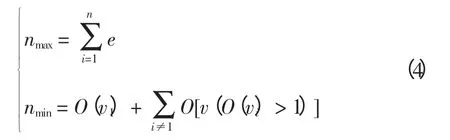
式中,O(v1)为根节点的出度。当n 取nmax时,称配电网支链为最短支链SBC(shortest branch chain),而当n 取nmin时,称为最长支链LBC(longest branch chain)。SBC 表示配电网负荷节点间的连通关系,主要用于建立开关表,一般情况下,已经给定。在生成网络初始状态的LBC 时,可先通过搜索SBC 首端节点出现的个数判断网络初始状态的节点出度,并按上述原则进行LBC 的划分。
1.2 支链邻接表
取nmin的情况,即按LBC 的划分方法建立支链邻接表。以图1 所示的配电系统为例,按DFS 法对系统节点编号,实线为分段开关,虚线为联络开关。
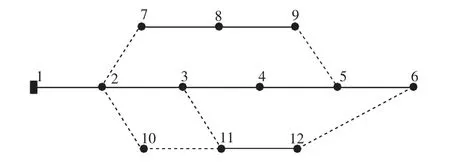
图1 配电系统Fig.1 Distribution system
对系统中的LBC 建立映射关系。定义支链内2端节点的逻辑关系为链接关系,并称供电节点为链首节点,受电节点为链尾节点,简称首、尾节点,若支链内存在非首尾节点,则统称为链中节点。联络开关两个端节点互为联络节点,称为联络节点对。
由DFS 编号特点:首节点编号大于尾节点,而在进行前推回代计算时,所有首节点必须在其所有尾节点前推完毕后才能进行前推。
按LBC 的划分方法:图1 中1 号节点为根节点,O(v2)、O(v3)大于1,记为首节点;节点O(v6)、O(v9)、O(v10)、O(v12)等于0,记为尾节点,将首节点按编号升序排列,得LBC 邻接表如图2 所示。
图2 邻接表标示了配电网正常运行时支链间和支链内的供电(前推回代)顺序。按表中的支链进行前推回代计算时,采用从右至左、自下而上的回代顺序,前推顺序与回代顺序相反。由于一条支链上不存在分支,故回带公式修改为
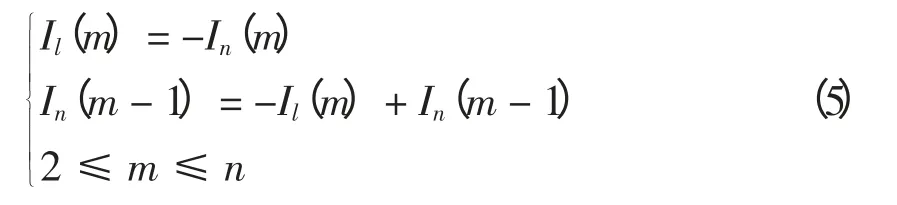
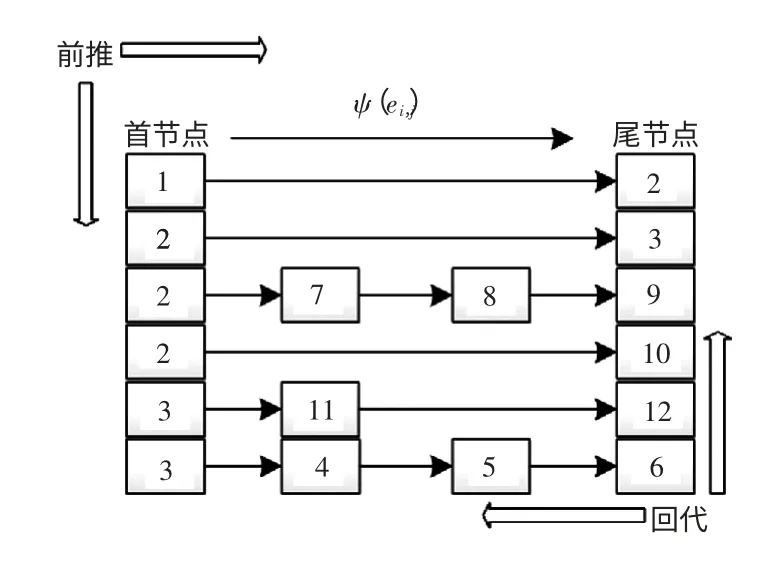
图2 LBC 邻接表Fig.2 LBC adjacency list
前推公式修改为
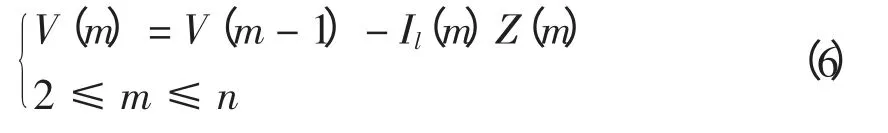
式中:Il为支路电流,A;In为节点注入电流,A;V 为节点电压,V;Z 为支路阻抗,Ω;n 为某支链包含节点总数。回带时,支路电流视为其供电节点的注入电流,并在下次回带时进行更新。采用修正后的前推回带算法进行潮流计算时,无需进行矩阵的乘法计算,且算法的空间复杂度较小。在满足潮流计算收敛条件后,需记录潮流分布结果。
2 拓扑结构快速适应算法
2.1 支链组环
文献[9]给出了配电网重构的支路交换算法,但在形成共源点的单环网时,需要逐步遍历环网的所有节点,并排除单环网的侧边,增加了遍历的复杂度。采用LBC 的划分方法,只需找到闭合开关的联络节点,将一侧的联络节点及其到环网源点所有支链的首节点,按序压入队列T,从另一联络节点开始向源点搜索,直到找到与T 中节点相同的源节点S。S 与联络节点间的支链集合即为环网。在形成队列T 时,将本次搜索支链的首节点作为下次搜索支链的尾节点,可避免侧边的影响。
忽略环网侧边,将联络节点到S 的2 个支链集合组成的映射关系命名为R、L。其中R 为高压侧支链,L 为低压侧支链。
对图1 的配电系统进行组环,令φ(e5,9)= 1,形成S = 2,T = {5,3,2},R = ψ(e2,3)+ ψ(e3,5),L =ψ(e2,9),包含联络节点5、9 的单环网如图3 所示。
按第1.1 节的支链划分方法,组成单环网的支链首节点均有侧边。若联络节点为其所在支链的链中节点,则将联络节点到该支链尾节点间的支链部分视作联络节点在环网中的侧边。记录单环网中存在侧边的节点编号及其侧边个数,并分别压入队列T1、T2。
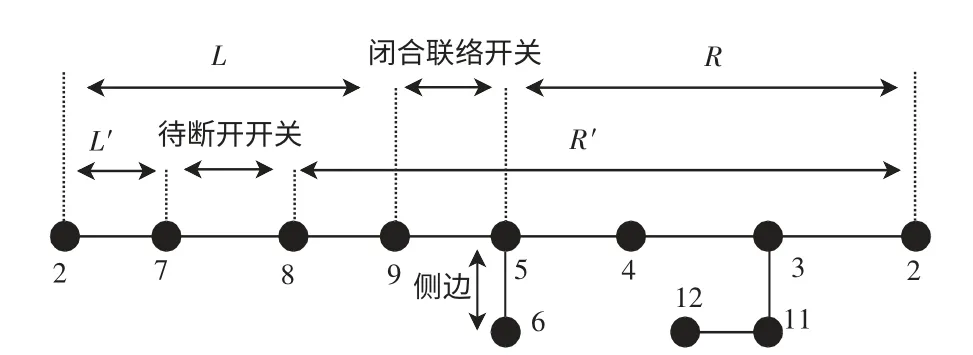
图3 单环网支链Fig.3 Branch chain of single-ring network
2.2 解环策略
对具有多环网结构的配电网,每次闭合一个联络开关形成一个单环网。将单环网侧边所在支链的供电电流视作支链首节点的注入电流,则单环网简化为没有侧边的单环网支链Sr。分别计算R、L 以及对应闭合联络开关的电阻,可得Sr电阻Rloop。
设系统无功补偿配置良好,则支路交换后的网损增量ΔP 的估算公式[10]为
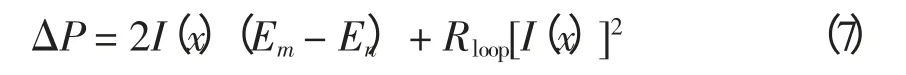
式中:I(x)为支路交换节点的注入电流;Em、En为联络节点相对环网源点的参考电压,式中的参数均为实数。式(7)为以I(x)为自变量的离散型二次多项式,为使网损下降,取Em〈En,即将负荷转移至高压侧,则使得网损下降的I(x)取值范围为
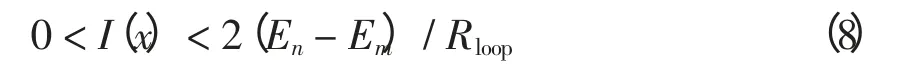
使得网损下降最快的I(x)应为式(7)的导数取0 的特殊点:I(x0)=(En-Em)/Rloop。且En-Em的差值应为所有联络节点对电压差值中满足约束条件下的最大值。由于自变量I(x)的离散特性,该点通常不能达到。故在满足式(8)的条件下,取低压侧转移负荷电流最接近I(x0)的负荷节点集合进行负荷转移。此时,若I(x)超出式(8)降损范围,则针对该单环网的重构不再具有降损效果。
对于已进行过重构的单环网,需要再次进行重构时,可沿支链L 向源点S 方向搜索,并判断是否超出式(8)范围,从而定位新的联络开关。
解环后的网络结构发生改变,需重新生成支链邻接表,其步骤如下。
步骤1 去除原有支链邻接表中属于Sr 的节点(不包含侧边),对Sr解环,闭合联络开关两侧节点出度加1,断开分段开关两侧节点出度减1,令i =1,以新产生联络节点对为起点,向源节点S 方向生成2 条无侧边的支链R′和L′,并开辟相应存储空间;
综上所述,机械电气一体化技术属于一种综合性技术,可广泛以应用到多个生产领域中,不仅保证了产品生产质量,也在一定程度上提升了生产的效率,具有无可比拟的优势。
步骤2 判断节点T1(i)是否为R′或L′的末端节点,是则转步骤3,否则转步骤4;
步骤3 若T2(i)= 1,则将与R′或L′直接相连的侧边所在支链追加到R′或L′的末端,合并为一条支链,并将该侧边从邻接表中去除,转步骤5,否则转步骤4;
步骤4 从R′或L′中划分出1 条以T1(i)为首节点的支链,尾节点为R′或L′的末端节点,将该支链重新加入支链邻接表,将R′或L′所在存储空间中,以T1(i)为首节点的支链移除,并将T1(i)节点作为R′或L′的末端节点;
步骤5 若i〈imax,i=i+1,转步骤2,否则,将新生成的支链加入支链邻接表。
上述解环策略能够自动更新节点出度,并确定新生成支链及支链内部的前推回代顺序,避免了网络重构后重新搜索SBC 和开关表。
采用前推回代法进行潮流计算的起始点为馈线末端,而馈线末端节点出度为0。按此原则,确定解环后支链间的前推回代顺序,并将支链存入新生成的邻接表。设此时邻接表共有jmax条支链,则生成新的邻接表的程序流程如图4 所示。
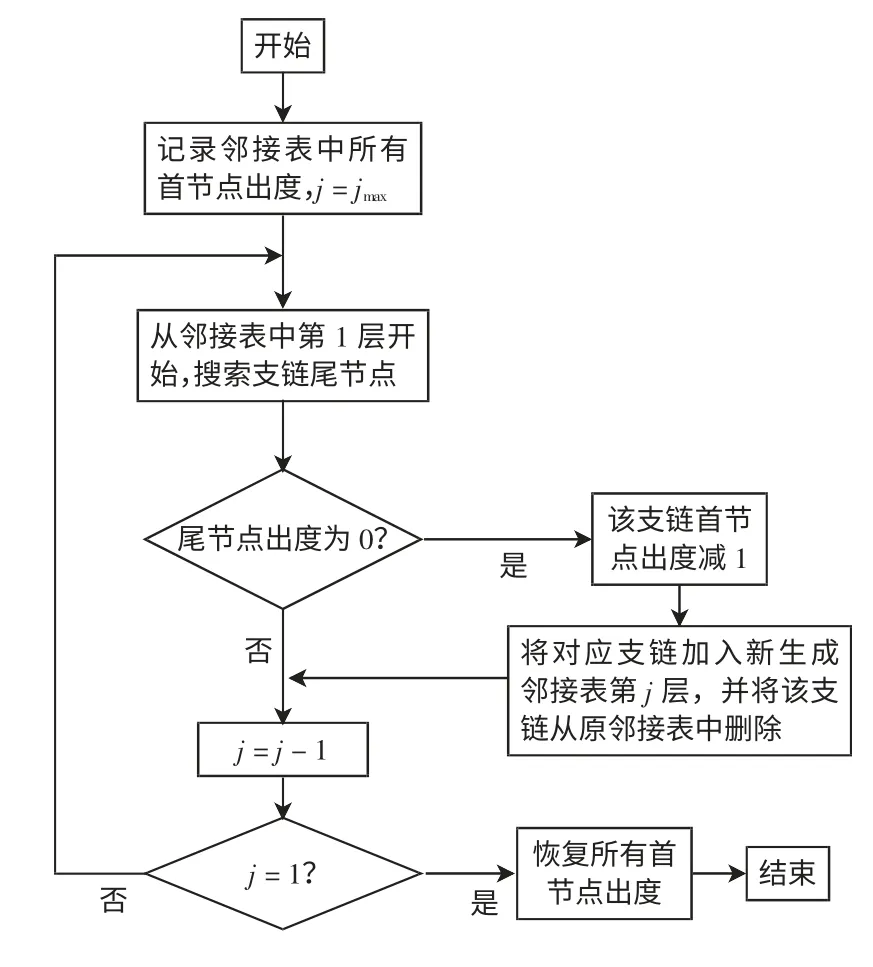
图4 支链间前推回代顺序流程Fig.4 Flow chart of the back/forward sweep sequence of different chains
按图4 得到修正后的支链邻接表,即可进行潮流计算,从而进行新的网络重构过程。按此方法进行迭代运算,直到找到配电网的最优结构。
综上所述,利用拓扑结构快速适应算法进行配电网重构的程序流程如图5 所示。
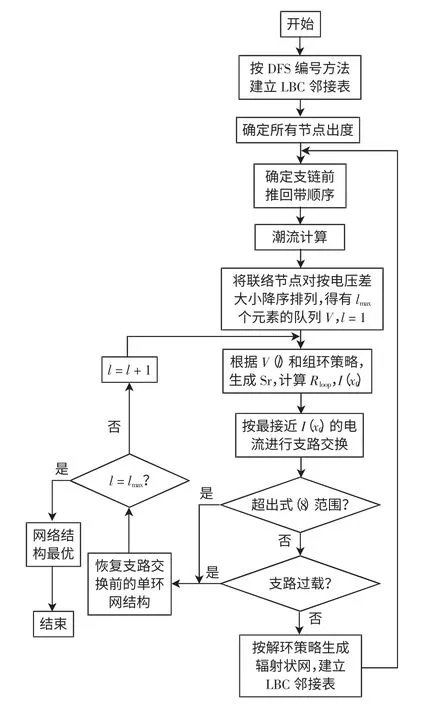
图5 拓扑结构快速适应算法流程Fig.5 Flow chart of the algorithm of rapid adaptation to the topological structure
3 算例
采用本文提出的方法,对IEEE33 节点配电系统进行网络重构。取基准电压为12.66 kV,基准功率为10 kW,初始网络结构所有节点均按照DFS的遍历方法进行编号,对33 节点重构前后生成的LBC 邻接表如图6 所示。计算得到的重构结果与文献[11]相同见图7 所示。
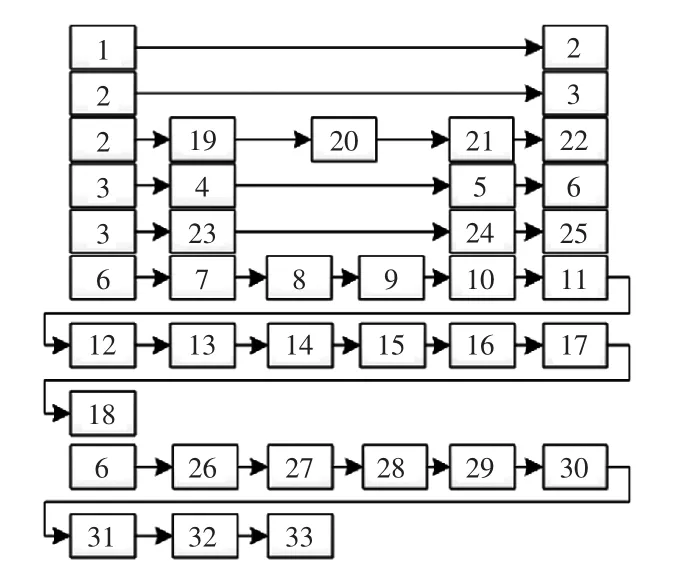
图6 33 节点系统LBC 邻接表Fig.6 Long branch chain adjacency list of 33-node system
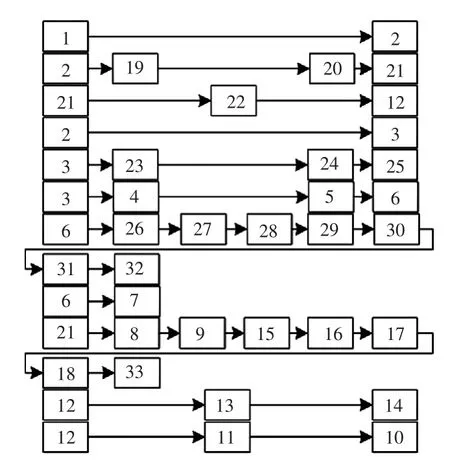
图7 33 节点系统重构结果Fig.7 Result of 33-node system reconfiguration
对比图6 和图7 可知,不属于任何环网的支链以及未发生支路交换的环网中的独立于其他环网部分的支链在LBC 邻接表中的结构没有发生改变,仅需调整前推回代顺序。每进行一次单环网重构时,采用邻接矩阵法和SBC 法需要重新确定环网上所有开关的操作顺序,且邻接矩阵法初始化时间较长,占用空间较大。而采用LBC 法描述的配电系统则充分利用了支链中已有的连接关系,快速确定环网结构,并在改变量较小的情况下得到重构后的配电网结构,无需对每个开关进行操作,相对于邻接矩阵法,减少了算法的时间复杂度和空间复杂度,提高了算法效率。
针对33 节点配电系统,分别采用邻接矩阵法、SBC 法与LBC 法描述配电网络,均采用支路交换法进行重构,对重构的效率做出了对比。在得到相同重构结果的同时,重构效率对比结果如表1 所示。

表1 重构效率Tab.1 Efficiency of reconfiguration
表1 中,迭代次数表示重构时产生的网络结构个数。可见,迭代次数相同时,采用LBC 法描述的配电网迭代时间更少,效率更高。
4 结论
(1)通过节点出度,建立了LBC 邻接表,用支链代替支路描述配电网结构,明确反映了节点间的连通关系。充分利用支链中已有的连接关系,快速确定环网结构,并在改变量较小的情况下得到重构后的配电网结构,避免了邻接矩阵法带来的时间和空间复杂度较大影响,提高了计算速度。给出了采用LBC 邻接表进行潮流计算的公式,该公式便于程序实现,且无需进行矩阵运算。
(2)解环时无需遍历开关表,且能够自动更新节点出度,快速生成新的支链,并确定LBC 邻接表的前推回代顺序。
[1]王丹,常宝立(Wang Dan,Chang Baoli). 一种用于配网潮流计算的节点编号新方法(A novel method of node numbering scheme on distribution system power flow calculation)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2003,15(1):22-26.
[2]杨仪松,王宽,周玲,等(Yang Yisong,Wang Kuan,Zhou Ling,et al). 一种配电网潮流计算的新方法(A new method for load flow calculation in distribution systems)[J].继电器(Relay),2006,34(13):46-49,76.
[3]刘莉,袁博,宛力(Liu Li,Yuan Bo,Wan Li). 基于关联矩阵自乘的配电网潮流计算(Distribution network flow calculation based on incidence matrix squaring)[J]. 电力自动化设备(Electric Power Automation Equipment),2005,25(8):53-55.
[4]谢开贵,周平,刘洋,等(Xie Kaigui,Zhou Ping,Liu Yang,et al).配电网络潮流计算的递推算法(Recursive load flow algorithm for electric distribution networks)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(4):36-39.
[5]Goswami S K. Direct solution of distribution systems[J].IEE Proceedings C,1991,138(1):78-88.
[6]刘莉,赵璇,姜新丽(Liu Li,Zhao Xuan,Jiang Xinli). 基于层次矩阵的配电网拓扑分析与潮流计算(Distribution network topology analysis and flow calculation based on layer matrix)[J].电力系统保护与控制(Power System Protection and Control),2012,40(18):91-100.
[7]邱生,张焰,孙建生,等(Qiu Sheng,Zhang Yan,Sun Jiansheng,et al).用邻接表保存中压配电网拓扑结构(Adjacency list saving topology structure of mid-voltage distribution system)[J].电力自动化设备(Electric Power Automation Equipment),2005,25(3):57-59.
[8]王威,韩学山,王勇,等(Wang Wei,Han Xueshan,Wang Yong,et al).一种减少生成树数量的配电网最优重构算法(A distribution network optimal reconfiguration algorithm of reducing the number of spinning trees)[J].中国电机工程学报(Proceedings of the CSEE),2008,28(16):34-38.
[9]Civanlar S,Grainger J J,Yin H,et al. Distribution feeder reconfiguration for loss reduction[J].IEEE Trans on Power Delivery,1988,3(3):1217-1223.
[10]毕鹏翔,刘健,张文元(Bi Pengxiang,Liu Jian,Zhang Wenyuan).配电网络重构的改进支路交换法(A refined branch-exchange algorithm for distribution networks reconfiguration)[J].中国电机工程学报(Proceedings of the CSEE),2001,21(8):98-103.
[11]张栋,张刘春,傅正财(Zhang Dong,Zhang Liuchun,Fu Zhengcai).基于改进禁忌算法的配电网络重构(Network reconfiguration in distribution systems using a modified TS algorithm)[J]. 电工技术学报(Transactions of China Electrotechnical Society),2005,20(11):60-64.

