串联电容补偿线路接地故障的行波测距新方法
宣文博,张艳霞
(天津大学智能电网教育部重点实验室,天津300072)
串补电容广泛应用在长距离超/特高压输电线路中,可以提高输送容量、优化潮流和系统稳定性[1-3]。但是,串补电容破坏了线路阻抗分布的均匀性,电容器过电压保护普遍采用具有非线性伏安特性的金属氧化物(MOV),这使常规的故障测距方法不再适用于串补线路。
目前有诸多关于串补线路故障测距的研究,一般分为两个思路:①求取串补电容两端的电压,将串补线路转化为两个普通线路进行故障测距,再判断故障点与串补电容的相对位置而确定故障点[4-7]。但是,MOV 的非线性使得串补装置两端瞬时电压的精确计算非常困难,影响了测距的准确性。②利用双端或者单端行波法进行故障测距[8-11]。通过各种数学工具和行波特征提取故障分量波头的到达时间计算故障距离,易受故障初相角、母线结构、行波衰减和畸变等因素的影响。此外,MOV 导通产生的暂态行波也可能对故障电流波头的识别形成干扰。
利用行波观点分析线路两端的电压电流,计算得到线路两端的正、反向行波,可以构成行波差动电流[12],普通线路正常运行时,其行波差流为零,但串补电容破坏了线路的均匀性,正常运行时其行波差流不为零。本文定义了适用于串补线路的行波差动电流,正常运行和区外故障时,该差流为零;区内故障时,该差流与线路参数、故障距离和故障电流相关。因为行波在零模和线模上的传输速度不同,差动电流的相角差只与故障距离相关,可据此实现故障测距。
1 不平衡差流补偿的行波差流
1.1 行波在均匀传输线上的传输特性
图1 中的mn 为单相均匀传输线,长度为L,波速为v,τ = L/v 为行波在线路全长上的传播延时,波阻抗为Zc,两端电流正方向为由母线流向线路,该电流可视为由正向电流行波和反向电流行波叠加构成。将正向电流行波定义为由左端流向右端,反之为反向电流行波,则各端2 倍的电流行波[12]为
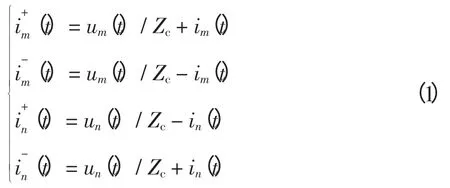
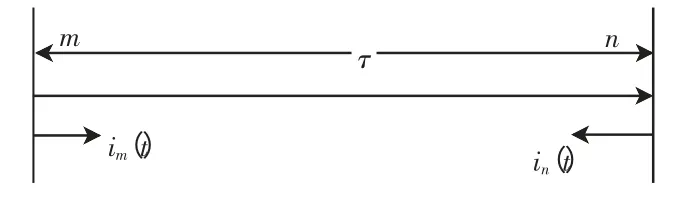
图1 单相均匀传输线Fig.1 Single-phase uniform line
描述均匀传输线上电压电流变化特征的偏微分方程为
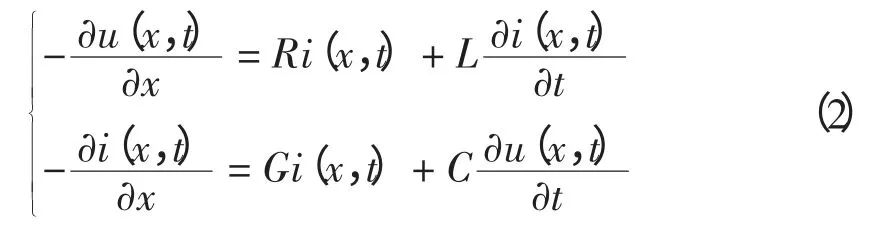
式中:R、L、G、C 为线路单位长度的参数;u(x,t)、i(x,t)为线路上x 点t 时刻的电压和电流。对于工频分量,解式(2)可得电流稳态解为

令γ=α+jβ 解得
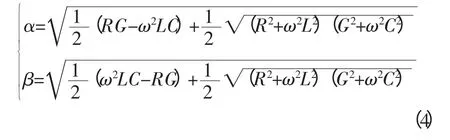
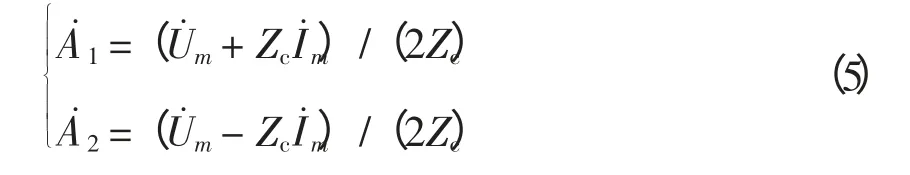

n 端的正向行波为
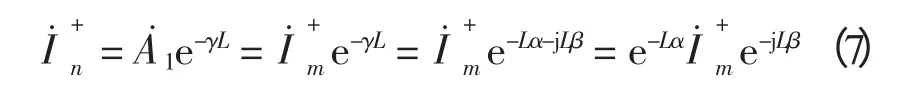
式中,e-Lα和e-jLβ分别表征了行波行进产生的幅值衰减和相移。
对于反向行波,经相似推导可得

1.2 串补线路行波差流的不平衡输出
图2 为串补线路,m 端到串补电容和n 端到串补电容的线路长度为Lmc和Lnc,L=Lmc+Lnc;传播延时分别为τmc和τnc,τ=τmc+τnc;uc1(t)和uc2(t)为串补电容两端电压,ic1(t)和ic2(t)分别为左侧和右侧流入的电流,大小相等、方向相反。线路两端至串补电容之间为均匀输电线,均满足行波传输方程。
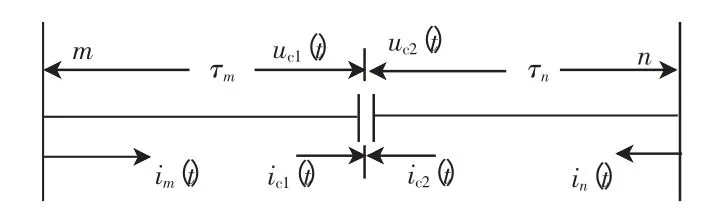
图2 串联电容补偿线路Fig.2 Series capacitor compensated line
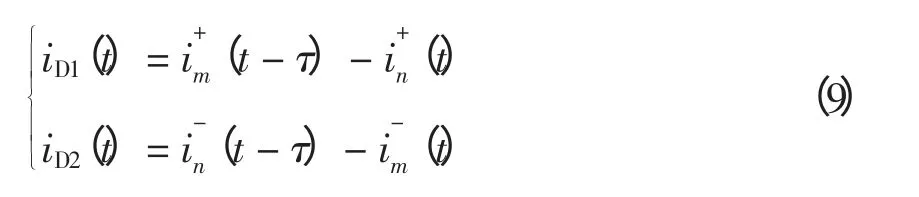
正向和反向的行波差动电流[11]为对于正向行波,m 端到串补电容安装处满足

式(10)两端同乘e-Lncαe-jLncβ得
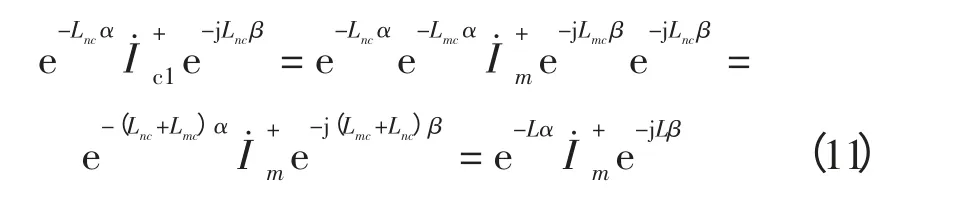
串补电容安装处到n 端满足

式(11)、(12)两端相减得
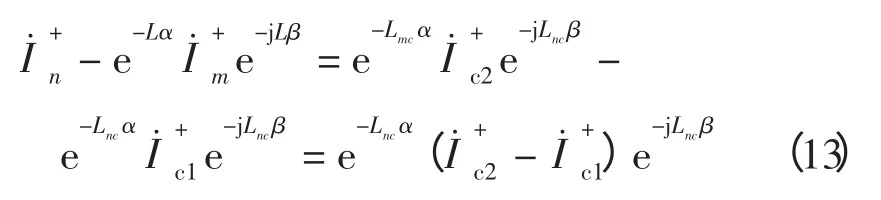
串补电容两端的正向行波电流可表示为
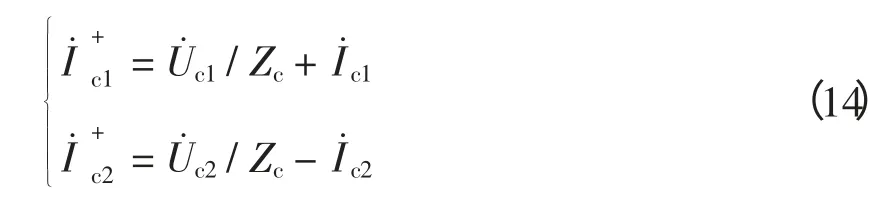
两式相减得:
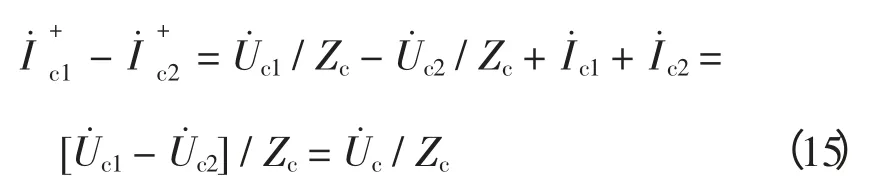
将式(15)代入式(13)化简得
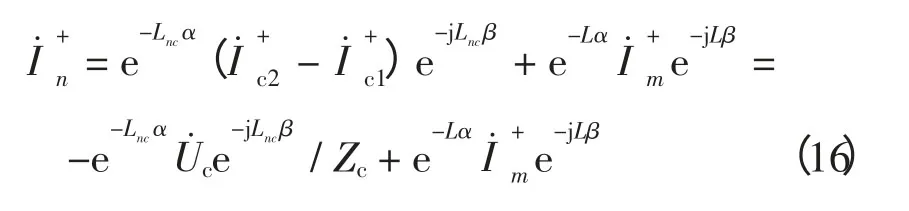
因此,正常运行或区外故障时正向行波差流为
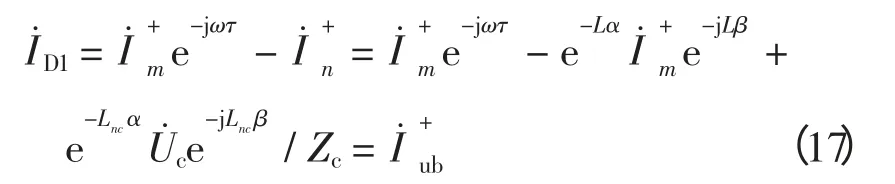
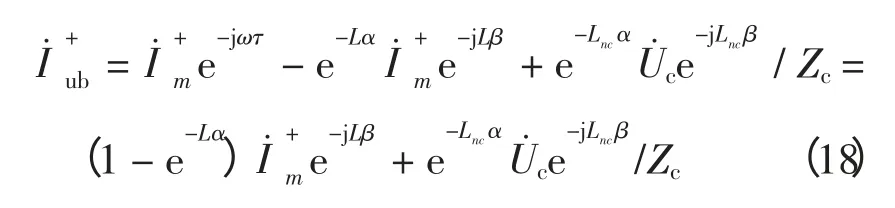
令不平衡系数μ=(1-e-Lα),则有
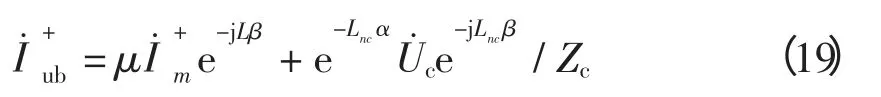
上式中,第一项为线损产生的不平衡电流,第二项为串补电容产生的不平衡电流。
对于反向行波,经相似推导可得
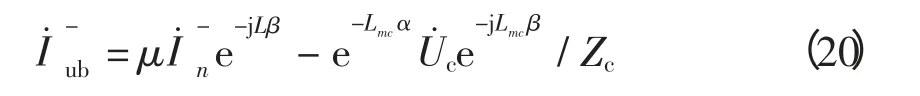
1.3 不平衡电流补偿的行波差流
为补偿线损产生的不平衡电流,定义经不平衡差流补偿的正、反向行波差动电流:
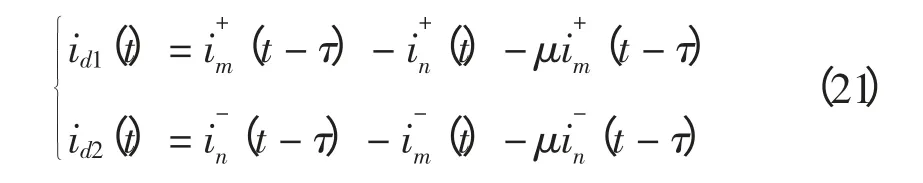
定义新行波差动电流为
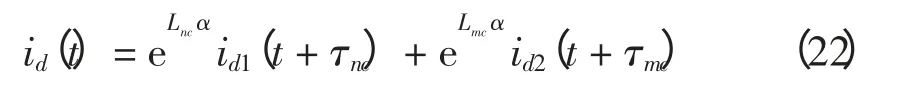
则正常运行和区外故障时的差动电流为
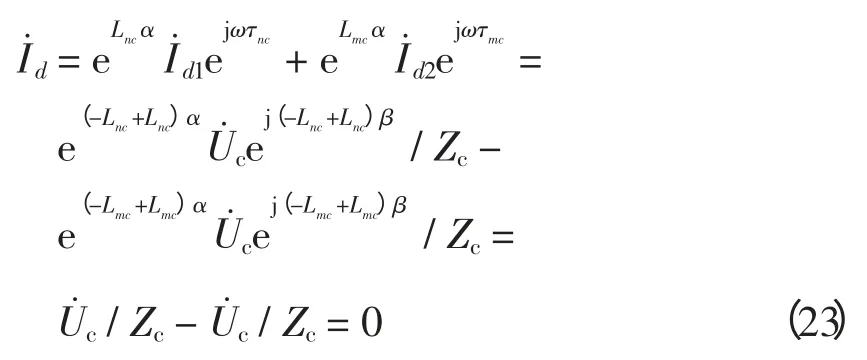
式(23)表明,串补电容分别在正、反向行波差动中产生的不平衡电流在新定义的行波差流中相对抵消为零。
串补电容和n 端之间的F 点故障时,如图3所示,从m 端到故障点,参考式(16)可得:
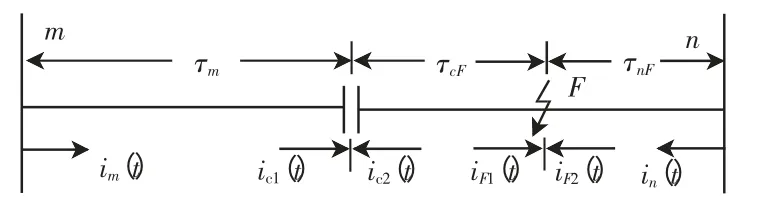
图3 串补线路内部故障示意Fig.3 Internal fault on series capacitor compensated line
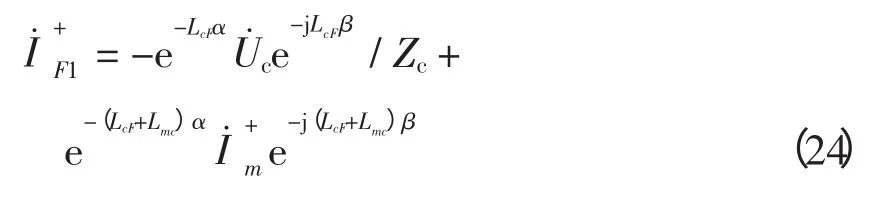
从故障点到n 端满足:

式(24)两端乘以e-LnFαe-jLnFβ,与式(25)相减得
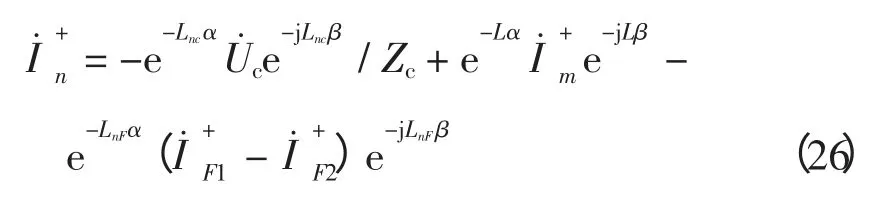
由于iF1(t)和iF2(t)的正向行波可表示为
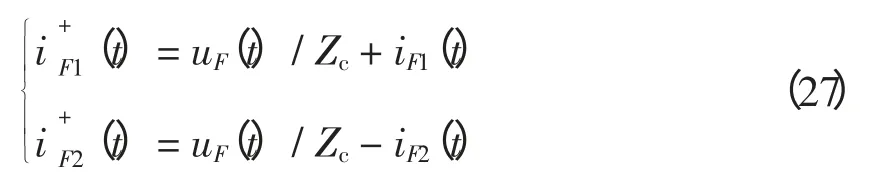
两式相减得
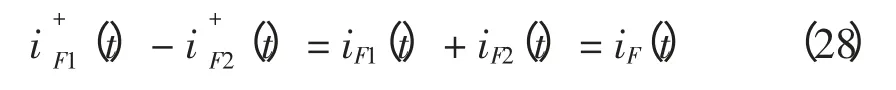
将式(28)代入式(26),化简得
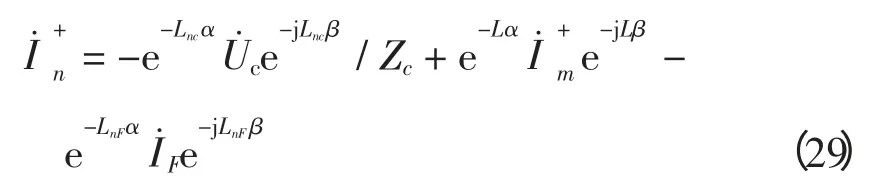
将式(29)代入式(21)中,得正向行波差流:
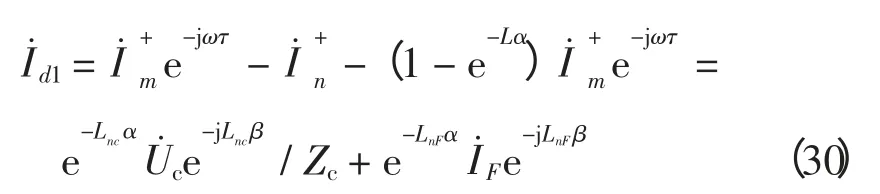
经相似推导,可得此时的反向行波差流:
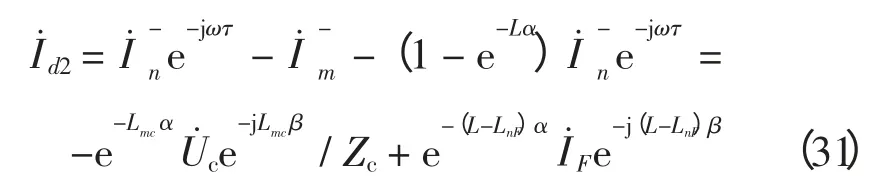
将式(30)、(31)代入式(22)可得行波差流I˙d为
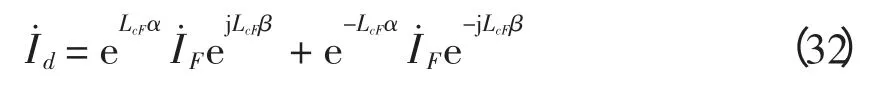
式(32)表明,线路内部故障时,行波差动电流I˙d由3 个因素决定:故障点至串补电容的距离LcF、故障点电流I˙F及线路参数(α、β)。
2 基于模量行波差动电流的接地故障测距
本文以卡伦鲍尔变换对三相线路实现解耦,变换矩阵为
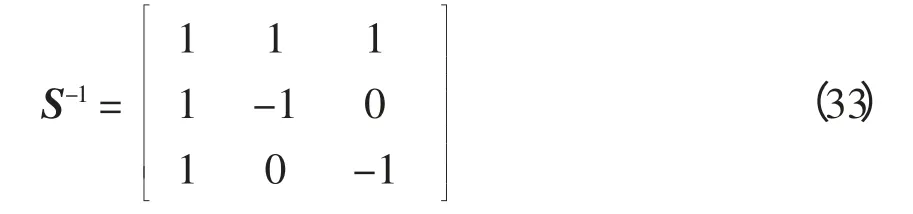
得到的0 模、1 模和2 模电流分别为
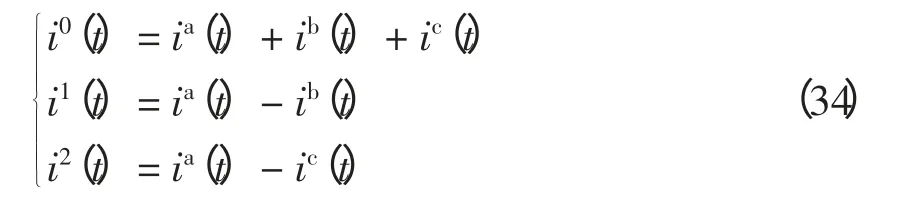
由式(34)可求得m、n 端电压电流的各模量测量值,进而计算得到m、n 端的各模正、反向电流行波,进一步计算得到经不平衡电流补偿的各模量行波差动电流利用地模和线模差动电流的相角差,可以对接地故障进行故障测距。
2.1 接地故障测距原理分析
线路内部故障时,按照式(32)各模差动电流可由故障点各模故障电流表示为
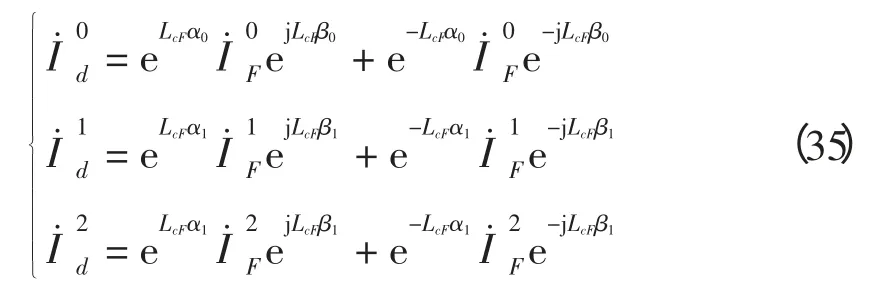
式(35)中故障点各模量故障电流计算式为
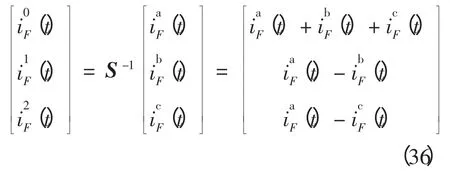
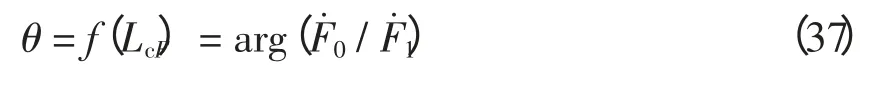
式(37)中,LcF与f(LcF)一一对映,存在反函数

相位差θ 由行波在地模和线模中传播速度的不同产生,其值较小,对于本文图7 仿真系统,θ 随LcF的变化曲线如图4 所示。
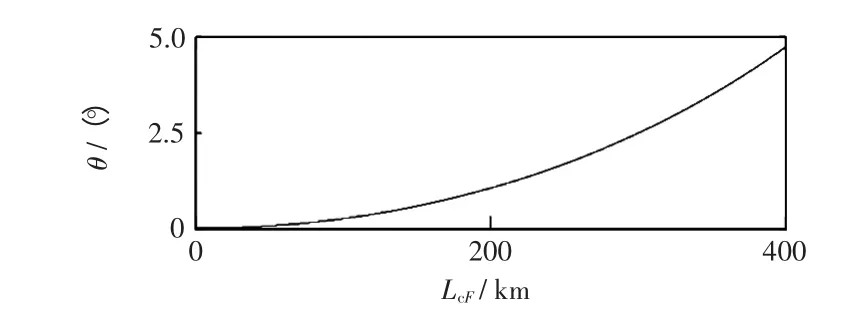
图4 的相位差Fig.4 Phase contrast between and
将式(36)代入式(35)求得各模量差动电流;依据故障边界条件,对各模量差动电流进行傅里叶变换得到表1。分析表1,可得以下结论。

表1 不同故障条件下各模差动电流Tab.1 Traveling wave differential currents of three modes in the cases of different faults
两相接地时,各模差动电流的相角差主要由故障相电流的相角差决定,由于F˙0与F˙1的相差相对很小,考察各模相角差时,忽略F˙0与F˙1带来的相差和幅值衰减不影响图5 分析结果的正确性。
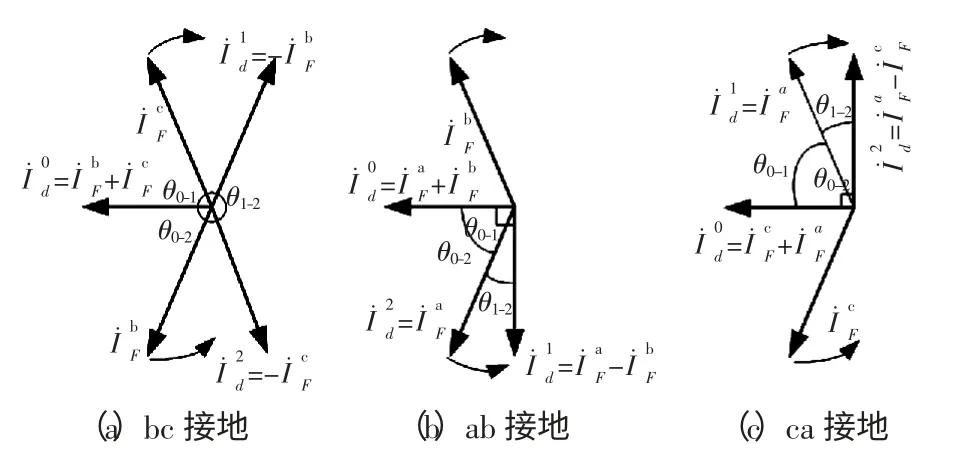
图5 两相接地相角差Fig.5 Phase angle difference with two-phase grounding fault
取θG1=30°,满足θ0-1〈 θG1,判为a 相接地,否则判为两相接地。
图5(a)金属性bc 接地时θ1-2为120°,随Rg增大至无穷大,θ1-2增大至180°,因此bc 接地120°〈θ1-2〈180°;图5(b)金属性ab 接地时θ1-2为30°,随着Rg增大至无穷大,θ1-2减小至0°,因此ab 接地0°〈θ1-2〈30°;图5(c)金属性ac 接地时θ1-2为30°,随着Rg增大至无穷大,θ1-2减小至0°,因此ca 接地0°〈θ1-2〈30°。
取θG2=90°,满足θ1-2〉θG2,判为bc 接地;否则判为ab 或ca 接地。
ab 接地和ca 接地依靠θ0-1和θ0-2的大小关系区分。ab 接地时,θ0-1和θ0-2的相角如图5(b)中所示,θ0-1〉θ0-2;ca 接地时,θ0-1和θ0-2的相角如图5(c)中所示,θ0-1〈θ0-2。因此,满足θ0-1〈θ0-2,判为ca 接地;否则判为ab 接地。
故障判别流程如图6 所示,IG为固定门槛值,按躲过正常和区外故障各模出现的最大不平衡电流整定。不同故障类型的测距方法也标在图中,具体分析如下:
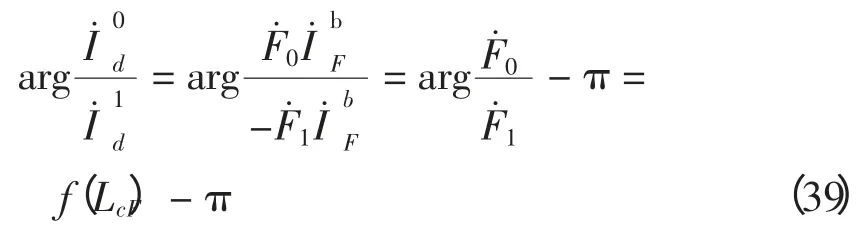

线路参数确定后,(θ0-1+π)与LcF的一一对映关系即为已知。
(2)c 相接地满足:
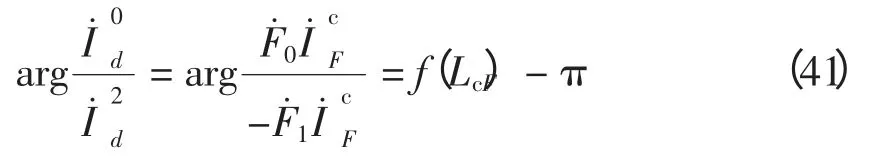

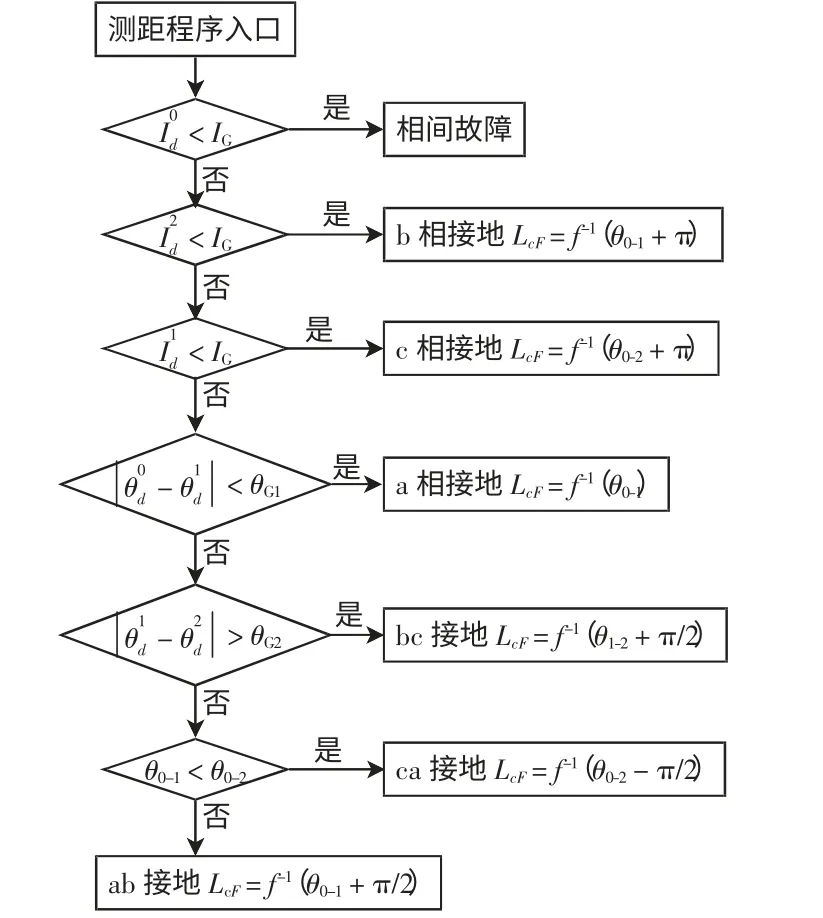
图6 测距流程Fig.6 Flow chart of fault location
(3)a 相接地满足
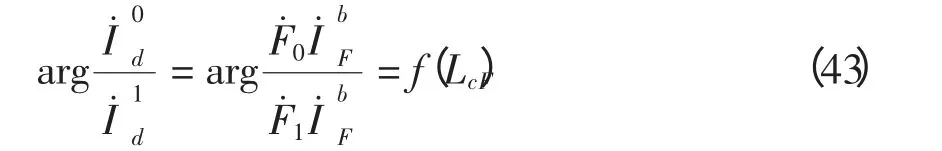

(4)bc 接地时,经分析可知
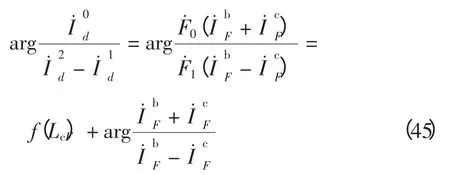
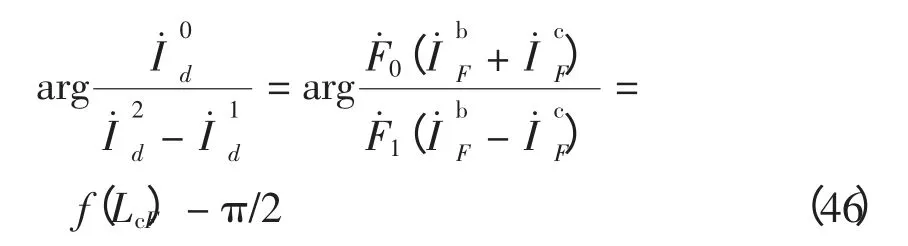

(5)ca 接地满足
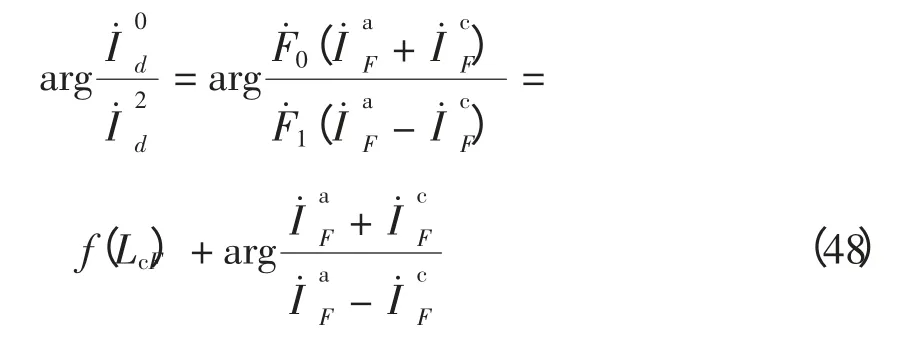
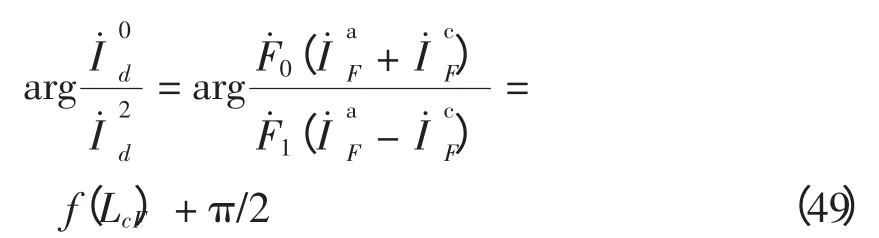

(6)ab 接地满足
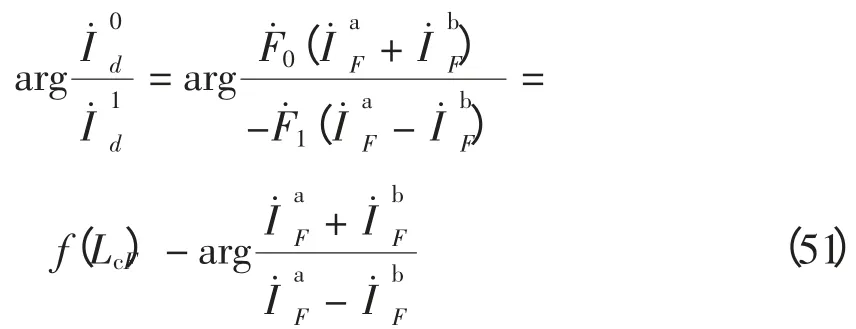
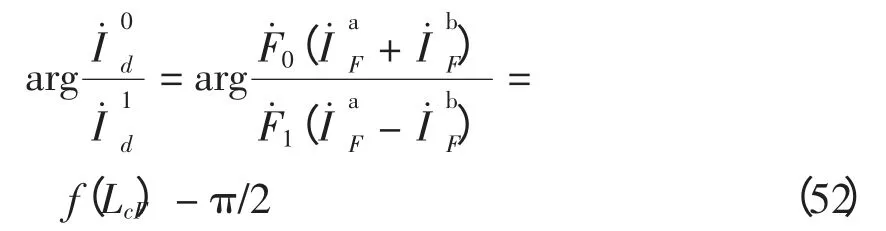

上述测距算法具有以下特点:①利用行波观点分析故障后线路电流的工频分量,只与线路对工频分量表现出的参数有关,通常意义上影响行波测距准确性的因素对本算法皆无影响;②测距公式中的相角差只是故障距离的函数,与过渡电阻和两侧系统阻抗无关,故不受过渡电阻及系统运行方式影响;③串补装置被视为线路上的间断点,其两端电压在I˙d中被补偿,I˙d与串补装置两端的电压无关,所以本原理不受串补装置的运行状态、MOV 的导通状态及MOV 的非线性特性的影响。
2.2 故障点位置识别
上文测距原理测量的是故障点与串补电容的距离。若串补电容安装在线路两端,则故障点位置唯一;若串补电容安装在线路中间,则故障点位置有两种可能,需要区分故障点与串补电容的相对位置。以m 端为参考端,故障位于串补电容与n 端之间时,认为串补后故障。由于串补上电压达到能使MOV 导通需要一段时间,文献[13]研究表明,最严重的情况下也需数毫秒,在这段时间内可以不考虑MOV 导通的非线性影响。利用该段采样数据,文献[14]通过微分方程求解电感参数构成距离保护,本文则通过串补电容表现出的参数特征识别故障点与串补电容的相对位置,简述如下。
故障点位于串补电容前,考虑过渡电阻Rg,微分方程为
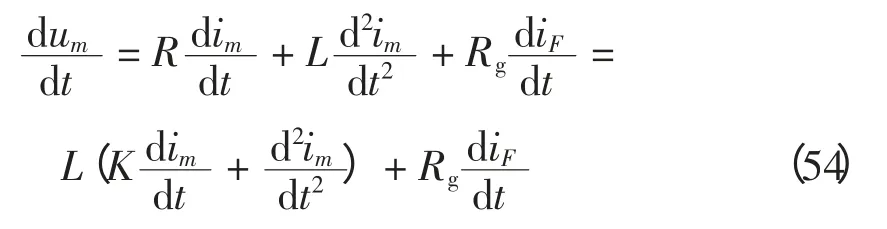
故障点位于串补电容后,考虑Rg但不考虑MOV 导通,方程为
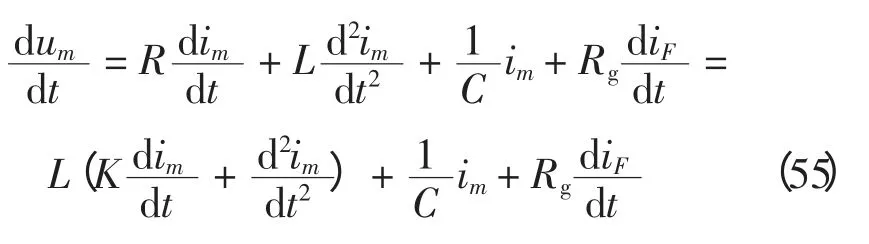
式(54)可视为式(55)中1/C=0 的特例,因此无论串补前还是后故障都满足式(55)。式中,um和im为测量值;K=R/L 为常数;iF为故障点电流由式(32)求得
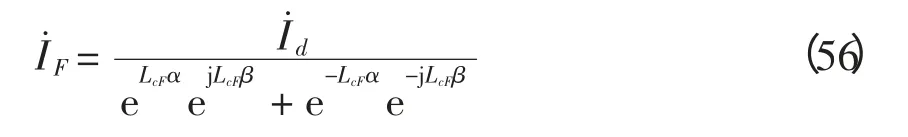
式中:LcF由测距算法求得;I˙d由两端测量值计算得到,线路参数(α、β)已知。可见,式中只剩下3 个未知参数L、1/C、Rg,利用冗余数据进行最小二乘法估计,可求得精确值。
串补电容前故障时,1/C 为零,所以求得的应很小;串补电容后故障,1/C 为额定电容的倒数,所以求得的1/C 应很大。因此判断故障点的相对位置的判据为

式中,CG取串补电容的额定值,可靠系数取k =0.5。满足式时,判为串补电容后故障,故障点距m端的距离LmF=Lm,c+LcF;否则,判为串补电容前故障,LmF=Lm,c-LcF。
3 仿真分析
在PSCAD 中搭建图7 双端系统,对本文测距算法进行了仿真验证。系统额定电压750 kV,线路全长400 km,串补电容补偿度40%、安装在线路中点。采用全波傅里叶算法作为滤波方式,采样频率为4 kHz。
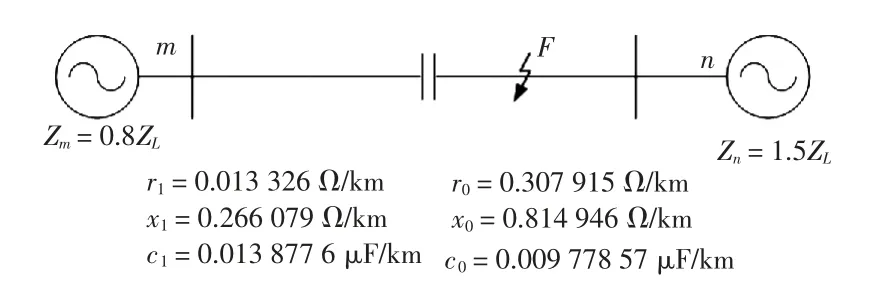
图7 串补线路模型Fig.7 Series capacitor compensated line simulation model
表2 给出了区内a 相接地的测距结果和误差分析,初相角取对行波测距最不利情况0°;测距结果为故障点至m 端的距离。
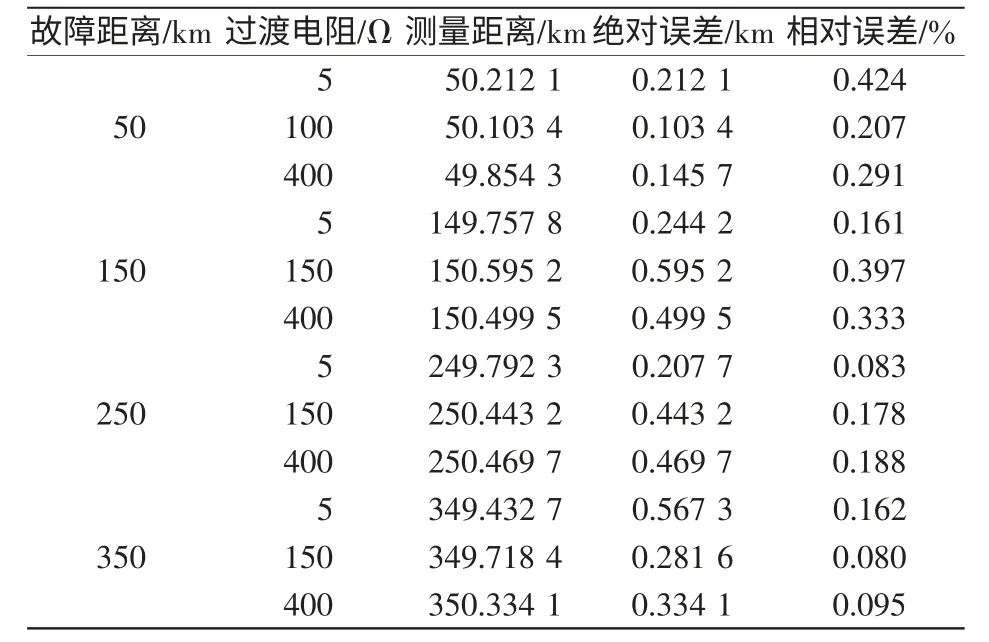
表2 仿真测距数据Tab.2 Fault location data by simulation
表3 给出了同一故障点不同接地故障类型的测距结果和误差分析。故障点距m 端350 km,过渡电阻400 Ω,故障初相角0°。
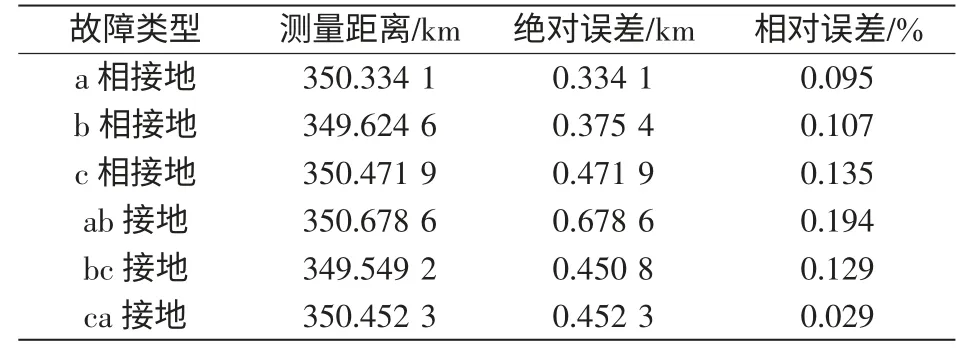
表3 仿真测距数据Tab.3 Fault location data by simulation
图7 所示为系统最小运行方式,设系统最大运行方式下的Zm=0.5ZL,表4 给出了系统运行方式不同,送电角δ 不同时,故障点距m 端350 km,a相经400 Ω 过渡电阻接地的故障测距结果和误差分析。
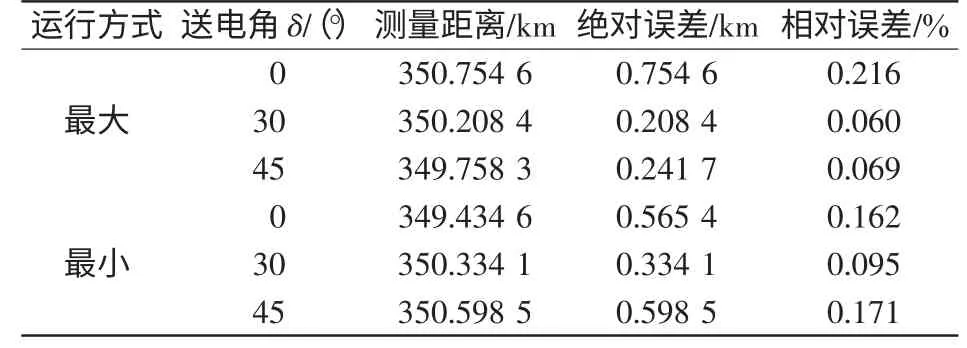
表4 仿真测距数据Tab.4 Fault location data by simulation
4 结论
本文利用行波在地模和线模的传播速度不同,提出了基于行波差动电流的串补线路单相接地测距算法,主要工作和结论如下:
(1)分析了串补线路正、反向行波差动电流的不平衡电流,定义了新的行波差动电流。外部故障时,不平衡电流得到补偿为零,线路内部故障时,差动电流是故障点电流和故障距离的函数。
(2)接地故障时,地模差动电流和线模差动电流的相角不同,其相角差是故障点位置的函数。
(3)差动电流与串补装置两端的电压无关,所以本原理不受串补装置的运行状态、MOV 的导通状态及MOV 的非线性特性的影响,适用于串补装置安装在线路中点和线路两端的各种情况。
(4)本文所提测距算法利用工频量,无需提取波头信息和波头到达母线时间,通常意义上影响行波测距精确性的因素对本算法皆无影响;不受过渡电阻和系统运行方式影响,继承了行波测距的优点;对采样频率无特殊要求,具有实用价值。
[1]贺家李,宋从矩.电力系统继电保护原理(增订版)[M].北京:中国电力出版社,2004.
[2]宣文博,张艳霞(Xuan Wenbo,Zhang Yanxia).串联补偿线路的距离保护研究(Study on distance protection for series-compensated lines)[J].中国电力(Electric Power),2012,45(6):5-9.
[3]王晓东,邰能灵(Wang Xiaodong,Tai Nengling).基于暂态能量的超高压串补线路故障选相(Fault phase selection for series compensated extra high voltage transmission lines based on transient energy)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(5):105-109.
[4]陈铮,董新洲,罗承沐(Chen Zheng,Dong Xinzhou,Luo Chengmu).带串联电容补偿装置的高压输电线路双端故障测距新算法(A new accurate two-terminal locating algorithm for series compensated line)[J]. 中国电机工程学报(Proceedings of the CSEE),2003,23(1):11-15.
[5]韩彦华,施围(Han Yanhua,Shi Wei).串补输电线路的精确故障定位算法(Accurate fault location algorithm for series compensated transmission lines)[J].中国电机工程学报(Proceedings of the CSEE),2002,22(5):75-77.
[6]束洪春,司大军,陈学允(Shu Hongchun,Si Dajun,Chen Xueyun).基于分布参数模型的串补线路故障测距方法研究(Study on locating faults on series compensated lines based-on distributed parameter line model)[J]. 中国电机工程学报(Proceedings of the CSEE),2002,22(4):72-76.
[7]陈允平,肖文峰,龚庆武,等(Chen Yunping,Xiao Wenfeng,Gong Qingwu,et al).一种基于微分方程法的串补线路精确故障测距算法(Accurate fault location algorithm for series compensated transmission line based on the differential equation method)[J]. 电 力 系 统 自 动 化(Automation of Electric Power Systems),2004,28(17):45-48.
[8]康忠建,徐丽,樊建川,等(Kang Zhongjian,Xu Li,Fan Jianchuan,et al).基于Hilbert-Huang 变换和神经网络的带串补高压输电线路故障测距(Fault location for high voltage transmission lines with the series compensation capacitor based on Hilbert-Huang transform and neural network)[J]. 电网技术(Power System Technology),2009,33(20):142-146.
[9]黄子俊,陈允平(Huang Zijun,Chen Yunping).基于小波变换的行波故障定位法在串补输电线路中的应用(Application of wavelet transform based travelling wave fault location to series compensated lines)[J]. 电 网 技 术(Power System Technology),2004,28(18):5-9.
[10]郑州,吕艳萍,王杰,等(Zheng Zhou,Lü Yangping,Wang Jie,et al). 基于小波变换的双端行波测距新方法(A new two -terminal traveling wave fault location method based on wavelet transform)[J].电网技术(Power System Technology),2010,34(1):203-207.
[11]全玉生,何秋宇,王倩,等(Quan Yusheng,He Qiuyu,Wang Qian,et al).串补线路的数学形态学行波测距法研究(New algorithm of traveling wave fault location for series compensated line using mathematical morphology)[J]. 高电压技术(High Voltage Engineering),2007,33(7):177-181.
[12]苏斌,董新洲,孙元章(Su Bin,Dong Xinzhou,Sun Yuanzhang).基于小波变换的行波差动保护(Traveling wave differential protection based on wavelet transform)[J].电力系统自动化(Automation of Electric Power Systems),2004,28(18):25-29,35.
[13]索南加乐,陈福峰,齐军,等(Suonan Jiale,Chen Fufeng,Qi Jun,et al). 串补线路故障点位置的模型识别方法(New method for identifying the fault location on series compensated lines based on different fault models)[J]. 中国电机工程学报(Proceedings of the CSEE),2005,25(1):66-72.
[14]王育学,尹项根,张哲,等(Wang Yuxue,Yin Xianggen,Zhang Zhe,et al).基于参数识别原理的串补线路距离保护(Distance protection for series compensation lines based on parameter identification principle)[J].电力系统自动化(Automation of Electric Power Systems),2011,35(14):98-102,111.

