末敏火箭弹约束期内动力学模型与研究
焦志刚,张晶晶,李建伟
(1 沈阳理工大学装备工程学院,沈阳 100159;2 中国兵器工业第203研究所,西安 710065)
末敏火箭弹约束期内动力学模型与研究
焦志刚1,张晶晶1,李建伟2
(1 沈阳理工大学装备工程学院,沈阳 100159;2 中国兵器工业第203研究所,西安 710065)
在筒内发射过程中,末敏子火箭弹的质量和质心位置随时发生变化,为研究末敏子火箭弹在筒内发射过程中的运动规律,采用Kane方法建立火箭弹在子弹筒内运动的约束期动力学模型,并对该模型进行Simulink仿真,得到在一定的落速、转速和初始扫描角条件下末敏火箭弹在发射过程中空间位置和姿态的变化规律。发射过程中稳态扫描角改变量与初始扫描角成正比,与发动机喷气的质量流率成反比;发动机推力偏心矩方向的随机性引起火箭弹扫描角的散布。
动力学模型;末敏火箭弹;六自由度;Kane方法
0 引言
末敏火箭弹系统主要包括降落伞、摩擦盘、扫描探测器、发射筒和火箭弹。把发射筒与火箭弹的组合视为末敏火箭弹,如图1。筒内发射阶段是指在稳态扫描并搜索到目标后,发动机点火到火箭弹前定心部脱离发射筒的阶段。末敏火箭弹的空间姿态是影响其射击精度的主要因素之一。该阶段,末敏火箭弹处于下落、转动和变质心的复杂运动中。建立末敏火箭弹筒内运动的动力学模型,得到其外弹道的初始条件很有必要。文献[1-2]分析了EFP末敏弹稳态扫描下的受力以及运动情况。文献[3]分析了单兵发射器发射过程动不平衡。
文中研究的末敏火箭弹筒内动力学模型为:发射筒依悬挂点由降落伞悬挂空中,当扫描探测器发现并确认目标后,火箭发动机点火工作。火箭弹在推力作用下沿发射筒轴线运动(无自转),随着发动机工作,火箭弹的质量减小且自身的质心位置发生变化,并沿发射筒向前运动。发射筒内壁受到发动机高速喷出的燃气流冲刷[2],火箭弹与发射筒之间相互摩擦,受到的力和力矩发生变化,空间姿态发生改变,并且绕悬挂摆动,不再保持初始的稳态扫描角。
1 基本假设
1)重力加速度为常数,不考虑地球科氏加速度与曲率的影响;2)末敏火箭弹无质量偏心,火箭弹定心部与发射筒之间没有间隙;3)不考虑降落伞的耦合作用,火箭弹与发射筒之间的作用瞬时响应;4)发射筒与火箭弹的摩擦力合力与发射筒轴线重合。

图1 末敏火箭弹示意图
2 坐标系建立与运动分析
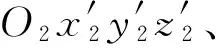
地面坐标系O1x1y1z1对末敏火箭弹悬挂点的空间位置进行描述,O1为稳态扫描状态下发动机点火瞬间悬挂点的地面投影点。O1x1轴为发射筒的轴线在发动机点火瞬间的地面投影且依火箭弹运动方向为正,O1y1轴沿铅垂方向且向上为正。O1z1轴由右手定则确定。


火箭弹辅助坐标系O4x4y4z4对火箭弹自身的质心改变进行描述。O4为火箭弹(不包含推进剂)的质心,3个坐标轴与坐标系O3x3y3z3三个轴分别平行且同向。

(1)

(2)

(3)
火箭弹在筒内运动任意时刻推进剂质量为:
(4)

(5)

图2 悬挂点平动坐标系与固连坐标系转换关系
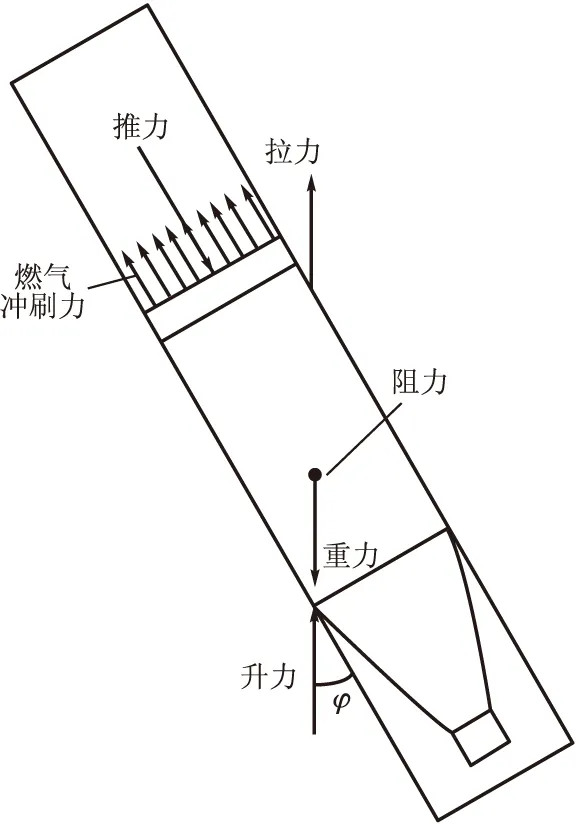
图3 末敏火箭弹受力示意图
式中:md为火箭弹(无推进剂)的质量。
火箭弹在坐标系O3x3y3z3下的质心位置为:
(6)
式中:l1为初始发射筒质心与火箭弹(不包含推进剂)质心距离;vd为火箭弹速度。
在固连坐标系O3x3y3z3下,末敏火箭弹的质心位置为:
(7)
式中:mt为发射筒质量。
3 受力分析

则火箭弹与发射筒的相互作用力为内力。发动机的推力作为特殊的外力改变火箭弹在发射筒中的位置,从而火箭弹组合体的质心位置发生改变。设推力Ft与火箭弹质心的夹角为φ,由于偏心方向与火箭弹在筒内的放置位置有关,仿真过程中随机生成偏心方向。
在坐标系O3x3y3z3的x3轴上,令:
(8)
式中:Rtd、Rdt为发射筒与火箭弹的摩擦力;Ftx为推力在O3x3轴方向的投影;R1为燃气冲刷力,文献[2]中给出燃气流冲刷力的公式。
火箭弹在筒内运动的全约束期时间段,火箭弹的推力为:
(9)
式中:ue为燃气速度;Ae为喷管出口面积;pe为喷管出口截面处的燃气压强;pa为外界大气压强。
火箭发动机在距离地面几百米高空工作,pe和pa相等时,喷管处于完全膨胀状态,火箭弹获得最大推力。则:
(10)
喷管质量流率:
(11)
式中:CD为流量系数;At为喷管喉部面积;Pc为燃烧室压强。
由文献[5]可知,燃烧室内压强随时间的变化近似于一次函数。设:
(12)
式中:C0、C1为压强函数系数;t0为点火瞬间到燃烧室恒定压强需要的时间。
文献[2]中发射筒的尾圈受力为零,由于火箭弹在筒内运动过程速度不大,忽略火箭弹头部的阻力。
随着末敏火箭弹质心位置发生变化,重力对悬挂点产生力矩。
令:
(13)
则重力力臂为:
(14)
在假设条件4)下,燃气冲刷力和摩擦力的合力与悬挂点的距离为d。合力矩的方向都垂直于O3x3y3面。记燃气冲刷力矩与摩擦力矩的合力矩为M1。

发射筒受到的合力R和合力矩M在发射筒固连坐标系下的投影为:
(15)
M=MG+M1+M2+M3+Mt=
(16)
4 Kane方法动力学方程
4.1 广义坐标
角速度由式(1)得:
(17)
末敏火箭弹的空间位置与姿态可由这6个广义坐标表示。广义坐标的时间导数作为广义速度,记为:
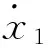
(18)
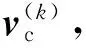
(19)
则:
(20)
引入偏角速度ω(k),末敏火箭弹的角速度为ω,则:
(21)
则:
(22)
4.2 广义主动力与广义惯性力
设Jc为末敏火箭弹对质心的惯量矩阵。筒内运动过程中,转动惯量Jc是随时间变化的。在计算时,先用Solidworks绘制火箭弹在发射筒内每移动2 mm时的三维设计图,记录下每个位置下末敏火箭弹的转动惯量,用高次多项式拟合成转动惯量-位移的Jc=Jc(xc)函数供Simulink仿真调用。
末敏火箭弹对悬挂点O2的惯量矩阵为:
(23)
由广义主动力公式:
(24)
广义惯性力公式:
(25)
(26)
(27)
补充公式:
(28)
整理式(4)~式(8)、式(10)~式(12)和式(28)可以求出末敏子弹的质心位置,即外力的作用点。
利用公式(24)、式(25)求解出末敏火箭弹的速度与角速度,然后积分确定末敏火箭弹空间位置。
5 Simulink仿真结果
采用末敏火箭弹的物理模型数据,稳态扫描参数为:初始扫描角为20°,周向摆角角速度为2 rad/s,落速15 m/s,应用Simulink对动力学模型进行仿真,以前定心部脱离定向筒为仿真终止条件,得到了筒内运动阶段的仿真结果。


图4 扫描角φ-时间曲线

图5 周向摆角α-时间曲线

图6 角速度时间曲线
末敏火箭弹在稳态扫描下,悬挂点只有y方向的位移,在83.5 ms内为1.2 m,当发动机工作后,悬挂点的位置在力与力矩的作用下,x、z方向也发生变化。图7为在膛内运动过程(83.5 ms)中,悬挂点相对于Ox1y1z1坐标系各坐标的变化曲线。该值是影响子弹落点散布分布的重要参量。
为了分析推力偏心对扫描角的随机影响,选取推力偏心矩与重力矩同向、推力偏心矩与重力矩反向、推力偏心矩与阻力矩同向、推力偏心矩与阻力矩反向的4种方案进行仿真,结果如图8所示。从上至下,第一条曲线为推力偏心矩与重力矩反向的扫描角变化曲线,第二条曲线为推力偏心矩与阻力矩反向的扫描角变化曲线,第三条曲线为推力偏心矩与阻力矩同向的扫描角变化曲线,第四条曲线为推力偏心矩与重力矩同向的扫描角变化曲线。

图7 悬挂点位移-时间曲线

图8 不同推力偏心位置的φ角-时间曲线
6 结论
针对末敏火箭弹筒内运动的研究,得到如下主要结论:
1)由方程可知,发射筒受到的摩擦力、燃气冲刷力是影响末敏火箭弹在x1轴方向上位移的主要作用力,减小发射筒摩擦力或增大发射筒冲刷力可以减小这种位移变化。图7表明,y1轴的位移差值为1.1 mm,与稳态落速在这段时间的移动距离1.2 m相比非常小,则视悬挂点为弹性连接是可行的。
2)推力偏心矩的方向对扫描角的变化有着很大影响。如图8所示,第一条曲线显示扫描角出现了增大的趋势,与其它3条曲线的变化规律明显不同,这是由于重力矩与推力偏心力矩反向,推力偏心距大于重力矩造成的。为了使末敏火箭弹的运动变化呈现规律性,减小扫描角的随机变化,应减小发动机的推力偏心。
3)扫描角的变化受到扫描角初始值的影响。由式(14)可知,减小初始扫描角φ值,重力的力臂变短,重力矩变小,扫描角改变量变小,不同扫描角的变化量相差很小。表1所示为初始扫描角25°、20°、15°下扫描角的变化量。

表1 不同扫描角的变化量
[1] 郭锐, 刘荣忠. 末敏弹刚柔耦合系统动力学模型及仿真 [J]. 兵工学报, 2007, 28(1): 10-14.
[2] 杨绍卿. 灵巧弹药工程 [M]. 北京: 国防工业出版社, 2010.
[3] 陈志坚, 林辉, 张海凌. 单兵武器发射器动不平衡冲量分析与计算 [J]. 弹箭与制导学报, 2008, 28(6): 164-166.
[4] 刘延柱. 高等动力学 [M]. 北京: 高等教育出版社, 2003.
[5] 唐金兰, 刘佩进. 固体火箭发动机原理 [M]. 北京: 国防工业出版社, 2013.
[6] 孙棕檀. 刚柔耦合系统分析动力学建模研究 [D]. 哈尔滨: 哈尔滨工程大学, 2013.
[7] 殷克功. 末敏子弹运动特性分析研究 [D]. 南京: 南京理工大学, 2008.
[8] 原渭兰. 气体动力学 [M]. 北京: 科学出版社, 2013.
Dynamic Model and Simulation of Terminal-sensitive Rocket Bomb in Constraint Period
JIAO Zhigang1,ZHANG Jingjing1,LI Jianwei2
(1 School of Equipment Engineering, Shenyang Ligong University, Shenyang 100159, China; 2 No.203 Research Institute of China Ordnance Industries, Xi’an 710065, China)
During terminal-sensitive rocket bomb launching in cylinder, mass and mass center position change over time. In order to analyze the law of motion during launch, the dynamic model of motion of rocket bomb in cylinder in the constraint period was established by Kane method and simulated by Simulink. It was concluded that the variation law of rocket bomb space position and attitude was simulated with certain falling velocity, rotational speed and scan angle. In the progress, the variable quantity of steady scan angle is proportional to initial scan angle and inversely proportional to mass flow rate of rocket engine. In addition, randomness of thrust eccentric direction causes scatter of scan angle.
dynamic model; terminal-sensitive rocket bomb; six degree-of-freedom; Kane method
2014-11-10
焦志刚(1963-),男,辽宁沈阳人,教授,硕士研究生导师,研究方向:弹药系统设计,终点毁伤理论,弹箭远程技术。
TG156
A

