末修弹脉冲控制参数约束条件研究

曹小兵,徐伊岑,常思江,姚晓宁

(1 无锡职业技术学院控制技术学院,江苏无锡 214121;2 南京理工大学能源与动力工程学院,南京 210094)



末修弹脉冲控制参数约束条件研究

曹小兵1,徐伊岑1,常思江2,姚晓宁1

(1 无锡职业技术学院控制技术学院,江苏无锡 214121;2 南京理工大学能源与动力工程学院,南京 210094)

针对低旋尾翼式脉冲末修弹脉冲冲量及其距质心距离参数的设计问题,建立了脉冲控制力及力矩作用下的六自由度弹道模型,推导了脉冲引起的速度偏角及弹轴摆动角速度的变化量,对脉冲扰动后的复攻角方程进行了解析求解,分析了脉冲对攻角运动的影响,并提出了脉冲冲量及其距质心作用距离约束条件。仿真结果表明:脉冲冲量及其距质心距离取值不当会造成飞行失稳,而根据建立的约束条件来取值,能有效控制最大攻角,保证飞行的稳定。

尾翼弹;弹道修正;脉冲发动机;飞行稳定性

0 引言

脉冲末修弹作为一种新型弹箭,由于成本相对较低,工程上易于实现,且精度提高幅度较大,因而受到了广泛关注[1-3]。在其研制过程中,如何合理的设计相关的脉冲控制参数是非常重要的问题。

文献[4-5]通过数值仿真表明,脉冲冲量及其距弹体质心距离越大,修正能力越大,但同时对攻角的扰动越大。若上述两个脉冲控制参数选取不当,会造成飞行失稳,大大降低命中精度,甚至导致弹箭意外坠落。Л.Н.雷申科等[6]在B.C.普加乔夫形式运动方程的基础上,研究了脉冲力矩对弹箭角运动特性的影响,推导出旋转稳定脉冲修正弹的角运动稳定判别式,其数学形式复杂,难以直接应用。G.R.Cooper等人[7]通过对六自由度弹道方程组的简化,推导了尾翼弹在脉冲作用下的角运动与质心运动解析解,其结论是基于平射假设前提,不适用于曲射弹道。文献[8]分析了横向脉冲作用对迫弹飞行稳定性的影响,在忽略滚转条件下,将攻角运动简化为平面运动,给出了脉冲冲量大小及其距质心作用距离的约束条件。实际上由于该类弹箭需要依靠滚转才能实现多次修正,攻角运动实为空间运动,因而文献[8]的研究结果有一定的局限性。

文中以某低旋尾翼式脉冲末修弹为研究对象,根据其特点建立了横向脉冲控制力及控制力矩作用下的六自由度弹道模型,将脉冲作用视为对攻角运动的强扰动,分析了攻角运动响应特性,并在此基础上提出一个基于最大允许攻角的脉冲冲量及其距质心作用距离约束条件,以期为同类脉冲修正弹的参数设计提供一定的参考。

1 六自由度脉冲控制弹道模型

1.1 瞬态脉冲控制力及控制力矩模型

选用文献[9]中的相关坐标系,设单个脉冲发动机的冲量为Iimp、推力为Fimp,脉冲作用时间为τ,脉冲距质心作用距离为Limp,脉冲发动机喷口顺时针方向相对于第一弹轴坐标系oη轴的夹角为γp,将脉冲控制力投影至弹道坐标系o-x2y2z2,脉冲控制力矩投影至第一弹轴坐标系o-ξηζ,可得:

(1)

(2)

其中:

(3)

(4)

式中其余各符号的具体含义可参见文献[10]。

1.2 等效平均脉冲控制力及控制力矩模型

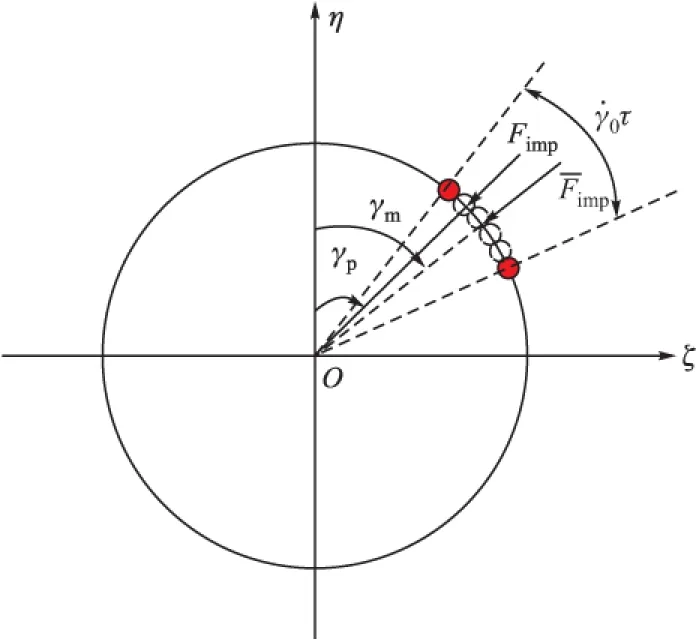
图1 瞬态脉冲控制力与等效平均脉冲控制力

设该转角角平分线顺时针方向相对于oη轴的夹角为γm,脉冲冲量的平均作用效果可沿此方向积分获得,相应的等效平均脉冲控制力表达式为

(5)

其在o-ξηζ三轴上的分量为:

(6)

等效平均控制力矩在o-ξηζ三轴上的分量为:

(7)

1.3 六自由度有控弹道模型

在六自由度无控弹道方程组中增加瞬态脉冲控制力及控制力矩即可得到瞬态有控弹道方程组,主要用于数值仿真。若代入的是等效平均脉冲控制力及控制力矩,则得到均态弹道模型,可用于解析分析。以均态模型为例,其质心动力学方程的标量形式如下:

(8)

绕心转动动力学方程的标量形式为:

(9)

式(8)～式(9)中:Fx2、Fy2、Fz2是无控时作用在弹体上的合力在o-x2y2z2三轴上的投影;Mξ、Mη、Mζ是无控时作用在弹体上的合力矩在o-ξηζ三轴上的投影;其余符号的含义参见文献[10]。

2 脉冲作用对攻角运动的影响

2.1 脉冲扰动下的攻角运动解析求解

考虑到脉冲发动机作用时间极短,为了从理论上弄清楚脉冲对攻角运动的影响,可将脉冲作用视为弹道上的强扰动,借鉴传统外弹道学中分析起始扰动对攻角运动影响的思路,研究脉冲作用后的攻角运动特性。

由式(8)、式(9)可以看出脉冲控制力将引起速度偏角的突变,而脉冲控制力矩则引起弹轴摆动角速度的突变,突变量为

(10)

式中:ψ1是高低偏角；φ1是高低摆动角。

(11)

根据微分方程理论,齐次方程的解反映了起始条件引起的运动,而低旋尾翼弹的复攻角齐次方程为:

Δ″+(H-iP)Δ′-(M+iPT)Δ=0

(12)

式中:H、P、M和T的表示式及含义同文献[9]。方程(12)的解为:

(13)

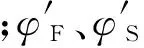
(14)

将式(11)作为脉冲发动机作用后复攻角运动的起始条件,代入式(13)及其一阶导数形式,联立方程后求得:

(15)

将式(14)和式(15)代入式(13),即可得到脉冲扰动下的攻角解析解。

2.2 脉冲扰动后的攻角运动特性分析

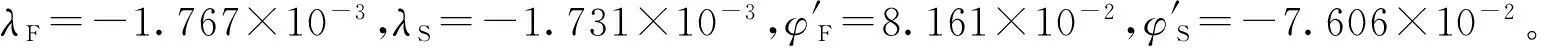
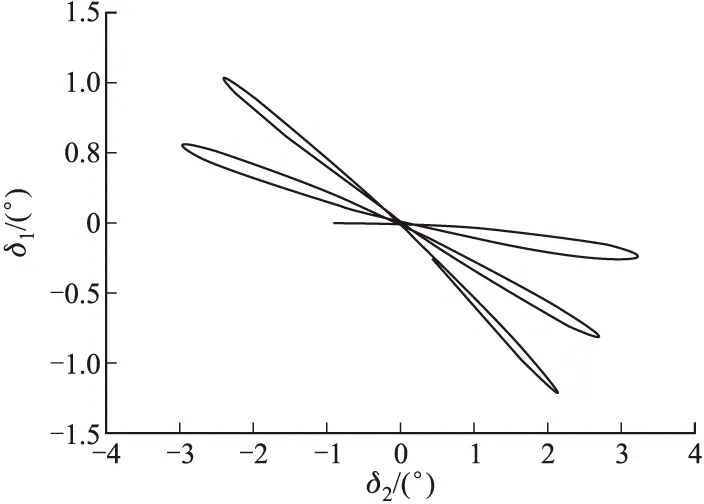
图2 复攻角运动曲线

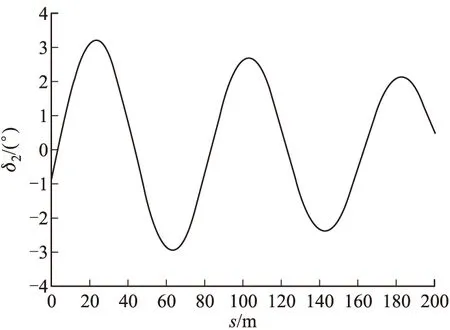
图3 攻角侧向分量随弹道弧长的变化曲线

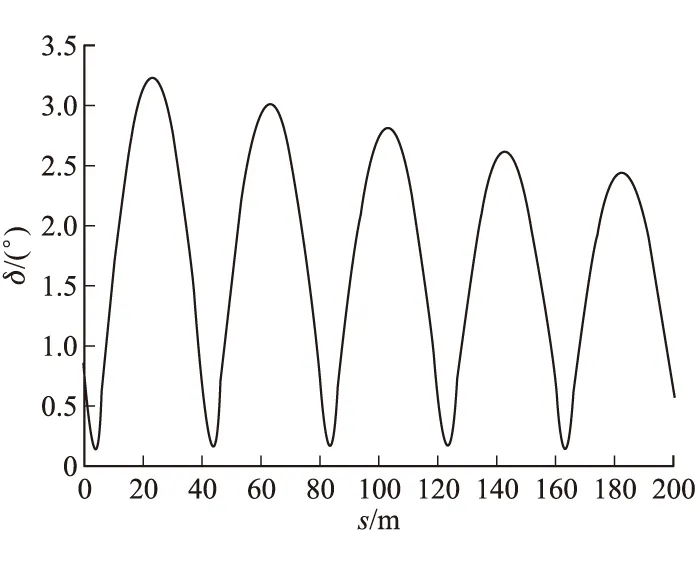
图4 总攻角幅值随弹道弧长的变化曲线

由于是向右作用,脉冲主要引起攻角侧向分量及其导数的变化。根据图2～图4可知:①脉冲控制力使得δ2从脉冲作用前的0°突变为-0.9°,此后在控制力矩引起的角速度的影响下近似按正弦规律振荡;②复攻角曲线呈现多叶多瓣形状;③总攻角幅值随弹道弧长呈现振荡,在赤道阻尼力矩的作用下其峰值逐渐衰减,最大峰值约3.3°。

3 脉冲冲量与距质心距离约束条件

上一节的分析表明,脉冲控制力及控制力矩将引起攻角的振荡,虽然赤道阻尼力矩有利于攻角幅值逐渐衰减,但如果脉冲冲量及其距质心距离两个参数选取不当,便可能造成攻角幅值在振荡中超过某上限,导致失稳。因此在初步设计时便应重点考虑这两个参数的选取。

(16)

利用欧拉公式,经过繁琐的推导,可将式(16)方括号中的第一项改写为如下形式:

(17)

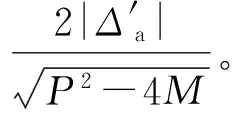
(18)

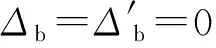
(19)

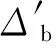
4 算例仿真及结果

为了检验所建立的限制条件的正确性,本节仍以2.2节提供的弹箭参数为例,取δL=15°,在零初始条件下,利用约束条件式(19)确定了4组不同Iimp-Limp组合,并将其代入编制的六自由度弹道计算程序进行数值仿真,得到了4组不同脉冲参数所引起的实际最大攻角δmax,计算结果如表1所示。

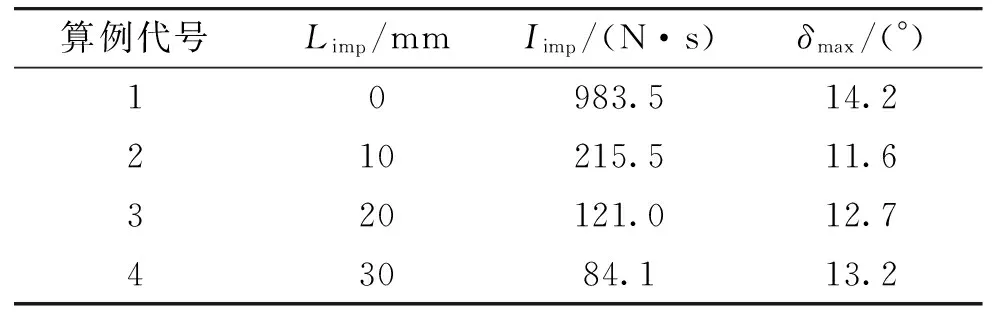
表1 不同Iimp-Limp引起的最大攻角

从表1可以看出,算例1条件下产生的最大攻角为14.2°,算例2至算例4条件下产生的最大攻角均未超过14°,4组条件下的最大攻角均小于给定的δL,这表明按照约束条件来设计脉冲冲量及其距质心距离,能有效限制脉冲引起的最大攻角,实现脉冲作用后弹箭的稳定飞行。

5 结论

1)脉冲控制力主要引起速度偏角的突变,而控制力矩主要引起弹轴摆动角速度的突变,两者共同决定了脉冲对弹箭攻角运动的影响。

2)在不破坏稳定飞行的前提下,脉冲引起的攻角幅值随弹道弧长呈现衰减振荡,而要保证脉冲作用后的飞行稳定,必须约束脉冲冲量及其距质心作用距离的取值。

3)提出的脉冲冲量及其距质心作用距离约束条件适用于低旋尾翼式脉冲末修弹,计算结果表明,利用该约束条件来指导取值能够将脉冲所引起的最大攻角值限制在允许值以内,从而保证脉冲作用不破坏弹箭的飞行稳定。研究结果为同类脉冲修正弹的参数设计提供了新的思路。

[1] Davis B, Malejko G, Dohrn R, et al. Addressing the challenges of a thruster-based precision guided mortar munition with the use of embedded telemetry instrumentation [J]. ITEA Journal, 2009, 30(1): 117-125.

[2] Gupta S K, Saxena S, Singhal A, et al. Trajectory correction flight control system using pulsejet on an artillery rocket [J]. Defence Science Journal, 2008, 58(1): 15-33.

[3] 谢金, 王朋飞. 脉冲式末端修正弹的修正能力及控制精度分析 [J]. 弹箭与制导学报, 2014, 34(6): 83-86.

[4] 曹小兵, 王中原, 史金光, 等. 火箭脉冲矢量控制弹道特性分析 [J]. 弹箭与制导学报, 2005, 25(3): 67-69.

[5] Corriveau D, Berner C, Fleck V. Trajectory correction using impulse thrusters for conventional artillery projectiles [C]∥23rd International Symposium on Ballistics, 2007: 639-646.

[6] 德米特里耶夫斯基 A. A. , 雷申科 Л H. , 波哥吉斯托夫 C. C. 外弹道学 [M]. 韩子鹏, 薛晓中, 张莺, 译. 北京: 国防工业出版社, 2000.

[7] Guidos B J, Cooper G R. Linearized motion of a fin-stabilized projectile subjected to a lateral impulse [J]. Journal of Spacecraft and Rockets, 2002, 39(3): 384-391.

[8] 曹小兵, 徐伊岑, 王中原, 等. 迫弹横向脉冲控制飞行稳定性 [J]. 弹道学报, 2008, 20(4): 41-44.

[9] 韩子鹏. 弹箭外弹道学 [M]. 北京: 北京理工大学出版社, 2008: 127-201.

[10] 曹小兵. 脉冲末修迫弹弹道特性分析与控制方案设计 [D]. 南京: 南京理工大学, 2012.

Research on Constraint Condition of Impulse Control Parameters forTerminal Correction Projectiles

CAO Xiaobing1,XU Yicen1,CHANG Sijiang2,YAO Xiaoning1

(1 Control Technology Institute, Wuxi Institute of Technology, Jiangsu Wuxi 214121, China; 2 School of Energy and Power Engineering, NUST, Nanjing 210094, China)

As for design of impulse magnitude and the distance from the mass center to individual thruster for low-spinning fin-stabilized terminal correction projectiles, 6-DOF model for the trajectory was established. The impulse induced changes of velocity deflection angle and oscillating angular velocity of body axis were derived. An analytic solution to the equation of complex angle of attack (AoA) after thruster operation was obtained. The effect of an impulse on the angular motion of AoA was analyzed. Then, a constraint condition of the impulse magnitude and the distance from the mass center to individual thruster was proposed. Simulation results show that the flight of projectiles may become unstable if the two parameters are chosen incorrectly. Using the constraint condition to determine the two parameters, the maximum value of AoA can be controlled under an allowed value, and the flight stability of projectiles can also be assured.

fin-stabilized projectile; trajectory correction; impulse thruster; flight stability

2014-04-06

中国博士后科学基金(2013M541676)资助

曹小兵(1982-),男,江苏海安人,讲师,博士,研究方向:导航、制导与控制。

TJ765.1

A