二维弹道修正榴弹动力平衡角与偏流特性分析

王 毅,宋卫东,孙燕青,卢志才

(1 解放军军械工程学院,石家庄 050003;2 总装备部工程兵科研一所,江苏无锡 214035)



二维弹道修正榴弹动力平衡角与偏流特性分析

王 毅1,宋卫东1,孙燕青2,卢志才1

(1 解放军军械工程学院,石家庄 050003;2 总装备部工程兵科研一所,江苏无锡 214035)

针对双旋结构旋转稳定榴弹的弹道特性进行研究。在固定舵和弹体无气动耦合的假设下,基于弹丸的运动方程和攻角方程,建立动力平衡角和偏流的解析表达式,并分析了各因素对动力平衡角和偏流的影响。仿真结果表明,舵片静力矩系数导数对动力平衡角影响较大,且随系数导数的增大动力平衡角减小;固定舵转速在一定范围内对偏流很大,并随转速增大而减小,转速大于该范围后,偏流受固定舵转速影响很小。该研究可用于弹丸的散布分析,为同类型弹丸的研究提供依据。

固定鸭舵;弹道修正;攻角方程;动力平衡角;偏流

0 引言

随着战争方式的演变,精确打击弹药成为当前研究的重点。而我军库存大量无控弹药,将其进行信息化改造使其具有一定打击精度是我军面临的重大课题。二维弹道修正引信在原有引信基础上集成了导航模块、姿态测量模块、修正控制模块等,仅替换原有引信即可实现弹道修正,是解决库存弹药信息化课题的首选方案。

当前所研发的二维修正引信均采用基于气动力的修正方案[1-3]。美国的CCF方案和PGK方案均选用了双旋结构,即引信修正组件与弹体绕弹轴成不同的滚转角速度。针对双旋结构,Costello M建立了7自由度刚体弹道模型[4],并采用线性化理论对弹道模型进行了线性化,进而分析了弹丸的稳定性问题[5]。为解决155 mm普通榴弹由高转速带来的实现修正困难的问题,法德圣路易斯研究院的Wernert P和Theodoulis S研究了基于双旋结构设计方案的弹道修正引信(CCF),引信头部有两对控制舵面,分别实现俯仰和偏航方向的控制,同时两对舵面可实现引信修正组件的减旋[6-7]。Wernert P介绍了采用一对固定舵面用于减旋,一对操纵舵面用于二维修正的引信设计方案,并依据Costello M的线性化理论对该型号弹丸的稳定性进行了分析[8]。我国对二维弹道修正引信的研究工作还处于理论研究阶段。王中原等提出一种基于阻力环修正射程、基于阻力板通过偏流修正侧偏的二维修正引信设计方案[9]。李伟、王志刚等在建立双旋制导火箭弹攻角方程的基础上分析了该型号火箭弹稳定性问题[10],并进行了蒙特卡洛打靶[11]。

基于固定鸭舵的修正控制方案具有活动部件少、可靠性高、可连续提供修正力的特点,是当前二维弹道修正引信研究中的热点,美国的PGK和MGK是该修正控制方案的典型代表。国内也在开展该修正控制方案的研究。郝永平、张嘉易等研究了舵片面积、翼展、翼型、舵偏角等因素与弹丸升力之间的关系,并分析了前置舵片对弹丸气动特性的影响[12-13]。纪秀玲等利用TVD格式求解N-S方程,采用双时间推进方法对带可旋转固定鸭舵的旋转弹丸的流场进行数值模拟,分析其俯仰特性随鸭舵方位角的变化规律[14]。

普通榴弹在安装固定鸭舵式二维弹道修正引信后,固定舵在来流作用下与弹体呈方向相反的角速度滚转。固定舵的反向滚转和固定舵与弹体之间的相互作用势必造成弹丸的动力平衡角、偏流等弹道特性发生变化,进而对弹丸的落点产生影响。文中以安装固定鸭舵式二维弹道修正引信的旋转稳定弹丸为研究对象,在建立攻角方程的基础上,推导了弹丸动力平衡角和偏流的解析表达式,并进行了研究分析。

1 弹道模型及攻角方程

1.1 弹丸动力学方程

安装二维弹道修正引信后,弹丸的受力将发生变化,其主要变化在于两对舵片产生的升力与力矩和固定舵运动产生的动态空气动力与力矩。假定固定舵与弹体间无气动力耦合,将弹丸所受的力和力矩在准弹体坐标系中分解,如式(1)、式(2)所示。

(1)

(2)

式中:Fx4、Fy4、Fz4为弹丸受力在准弹体坐标系各轴分量;Mxf、Mxa分别为固定舵和弹体所受力矩在x4轴的分量;My、Mz为弹丸所受力矩在y4轴、z4轴的分量;m为弹丸质量。

弹丸动力学方程如下:

(3)

(4)

1.2 攻角方程

在小攻角和小侧滑角情况下,vy4、vz4、r、q均为小量,可近似认为:

(5)

对上式求导,并略去小量乘积,则有:

(6)

将式(1)代入上式,可得:

(7)

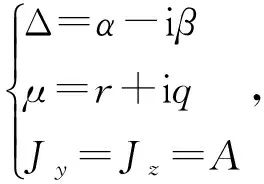
Δ″+(H-iP)Δ′-(M+iPT)Δ=G+D

(8)

式中,G和D分别为重力项和控制力项,且有:

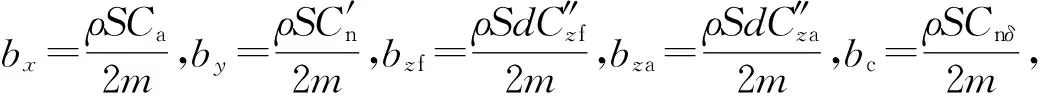
(9)

该方程考虑了弹丸飞行过程中的除非定态阻尼力矩外的所有受力和力矩,适用于包括旋转稳定弹、尾翼稳定弹的所有弹丸,且适用于火箭弹的无控段。

2 动力平衡角

方程(8)为线性非齐次微分方程,其解满足可迭加性。动力平衡角是由攻角方程的重力非齐次项解出的弹轴运动的平均位置,因而动力平衡角解析表达式即为方程(10)的一个特解。

Δ″+(H-iP)Δ′-(M+iPT)Δ=G

(10)

令Δ0=c1el1s+c2el2s为方程的一个特解,其中l1、l2为齐次方程的特征方程的两根,即:

(11)

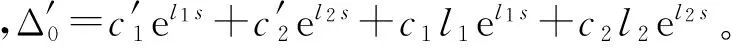
(12)

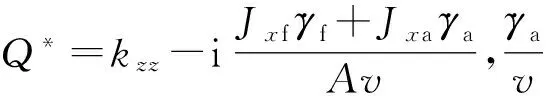
(13)

故有:

(14)

将分母实数化,可得:

(15)

式中δα、δβ分别为动力平衡角的实部、虚部。M、PT、kzz均为小量,且M2≫P2T2,则有:

(16)

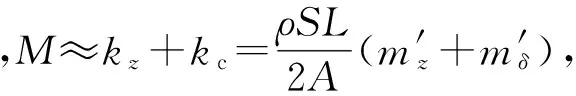
(17)

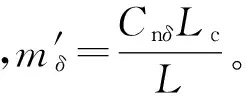
3 偏流

质点弹道是弹丸飞行弹道的一次近似。该弹道由重力和零升阻力确定,且弹丸以零攻角飞行。而飞行过程中弹丸还将受到其他空气动力和力矩的作用,攻角和侧滑角的出现将使弹丸受力更为复杂,造成弹道轨迹偏离质点弹道的结果。弹丸质心垂直于质点弹道的运动称为偏向运动。

假定偏向运动分量分别为yp、zp,则有:

(18)

将动力平衡角表达式代入即可解出弹丸偏向运动。

将式(16)代入上式,得:

(19)

将上式积分,可得:

(20)

升力项、马格努斯力项和PT为小量,可略去。则有:

(21)

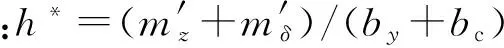
4 仿真分析

文中以某型大口径榴弹为研究背景,弹道模型与弹丸的气动参数已经过某基地飞行试验校核。为确保仿真的有效性,仿真初始条件采用飞行试验的初始条件,如表1所示。气象条件采用标准气象。

表1 仿真初始条件

4.1 弹道轨迹比较

普通榴弹在加装二维弹道修正引信后,由于舵片的作用将会使弹丸阻力增大[12],造成弹丸射程的损失。同时,由于舵片的受力将使弹丸整体压心前移,影响弹丸的弹道特性。

图1为普通榴弹和安装固定鸭舵式二维弹道修正引信的榴弹(简称双旋二维修正弹)的弹道曲线,弹丸落点见表1。安装鸭舵后弹丸射程减小约1 km,侧偏同时减小约100 m。可见,固定鸭舵式二维弹道修正引信的安装将对弹丸弹道产生巨大影响。

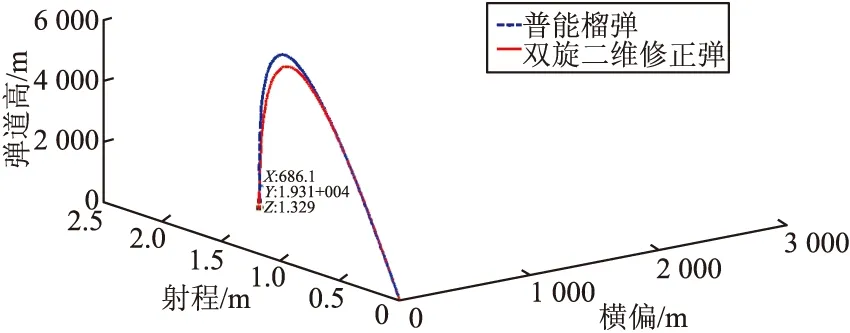
图1 两种型号弹丸弹道轨迹

表2 弹丸落点在发射系坐标

4.2 动力平衡角分析

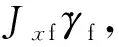
(22)

若上式中略去舵片产生的空气动力矩,则有:

(23)

即为普通榴弹的动力平衡角。

安装固定鸭舵式二维弹道修正引信后,弹丸动力平衡角的变化主要受舵面产生的静力矩系数导数和固定舵转速影响。

1)两种弹丸动力平衡角对比

与式(22)相比,式(23)分母中没有舵片产生的空气动力矩项,且普通榴弹的滚转阻尼力矩仅由弹体产生,转速较高,故其动力平衡角较大。图2中双旋二维修正弹的动力平衡角曲线出现了抖动,该抖动由舵面产生的静力矩引起,且产生的静力矩越大,抖动越大。

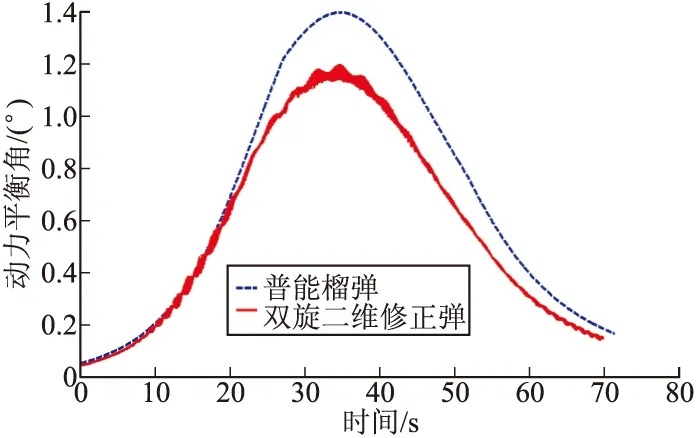
图2 两种型号弹丸的动力平衡角曲线

2)舵面静力矩系数导数对动力平衡角的影响

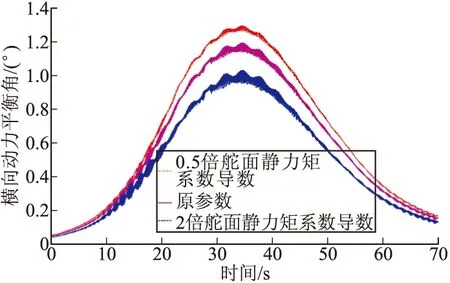
图3 动力平衡角随舵面静力矩系数导数的变化曲线

双旋二维弹道修正弹在最大弹道高处动力平衡角最大,约为1.2°。若舵面静力矩系数取为原气动参数的0.5倍,动力平衡角将增大到1.3°;若取为原参数的2倍,动力平衡角将减小为1°,如图3所示。

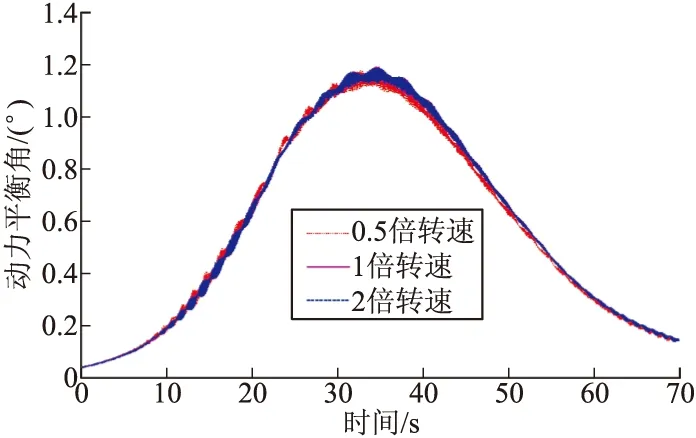
图4 动力平衡角随固定舵转速的变化曲线

4.3 偏流分析

由式(21)可知,压心到质心的距离h*越小,弹体极回转半径Rc越大,弹体转速越高,射角和落角越大,弹丸飞行时间T越长,偏流越大;反之,偏流越小。任意改变式(21)中的参数都将使飞行时间T等其他参数发生变化,因而,很难用仿真的手段定量的分析某一参数对偏流的影响。

1)两种弹丸偏流分析

两种弹丸的弹体极回转半径Rc值和落角近似相等,射角相同,造成偏流不同的因素在于压心到质心距离h*、弹体转速和弹丸飞行时间。普通榴弹转速最高、飞行时间最长,虽然h*相对偏小,但并未对偏流造成较大影响,偏流较大,如表2所示。

若固定舵与弹体滚转方向相反,即p*<0,固定舵转速越大,则1+p*越小。然而由于两者间的相互作用,固定舵转速增大将间接引起弹体转速的减小。因而,偏流量不会随固定舵转速的增大持续减小。如表3所示,当转速分别为0.5倍和0.8倍额定转速时,弹丸偏流分别为789.93 m和735.97 m,满足固定舵转速越高偏流越小。当固定舵转速超过额定转速时,偏流值并未随固定舵转速的增加而增加,而是变化很小。

表3 偏流随固定舵转速变化

5 结论

文中在推导安装固定鸭舵式二维弹道修正引信的大口径榴弹攻角方程的基础上,研究了旋转稳定弹丸由于重力非齐次项造成的动力平衡角,进而推导了弹丸偏流的解析表达式,得到如下结论:

1)动力平衡角受舵片引起的静力矩系数导数影响最大,静力矩系数导数越大动力平衡角越小,而固定舵转速对动力平衡角影响不大;

2)影响偏流的因素较多,如飞行时间、射角和落角、弹体转速、弹体总体参数等;固定舵转速在某一范围内对偏流影响很大,并在该范围内随固定舵转速的增大而减小,当转速超过该范围,偏流不再随固定舵转速的增大而增大。

文中推导了安装固定鸭舵式二维弹道修正引信的弹丸的动力平衡角和偏流的解析表达式,并分析了动力平衡角和偏流的影响因素,为弹丸的散布分析打下了基础,对该型号弹丸的研究具有重要意义。

[1] 张民权, 刘东方, 王冬梅, 等. 弹道修正弹发展综述 [J]. 兵工学报, 2010, 31(2): 127-130.

[2] Costello M. Modeling and simulation of a differential roll projectile [C]∥Proceedings of the 1998 AIAA Modeling and Simulation Techologies Conference, 1998: 490-499.

[3] Clancy J, Bybee T, Friedrih W. Fixed canard 2-D guidance of artillery projectile: US 6981672 B2 [P]. 2006.

[4] Eric Gagnon, Marc Lauzon. Course correction fuse concept analysis for in-service 155 mm spin-stabilized gunnery projectiles [C]∥Proceedings of the 2008 AIAA Guidance, Navigation and Control Conference and Exhibit, 2008: 1-20.

[5] Costello M, Allen Peterson. Linear theory of a dual-spin projectile in atmospheric flight [J]. Journal of Guidance, Control and Dynamics, 2000, 23(5): 789-797.

[6] Wernert P, Theodoulis S. Modelling and stability analysis for a class of 155 mm spin-stabilized projectiles with course correction fuse(CCF) [C]∥Proceedings of the 2011 AIAA Atmospheric Flight Mechanics Conference and Exhibit, 2011: 1-13.

[7] Theodoulis S, Gassmann V, Wernert P. Guidance and control design for a class of spin-stabilized fin-controlled projectiles [J]. Journal of Guidance, Control and Dynamics, 2013, 36(2): 517-531.

[8] Wernert P. Stability analysis for canard guided dual-spin stabilized projectiles [C]∥Proceedings of the 1998 AIAA Atmospheric Flight Mechanics Conference, 2009: 1-24.

[9] WANG Zhongyuan, CHANG Sijiang. Impact point prediction and analysis of lateral correction analysis of two-dimensional trajectory correction projectiles [C]∥9th International Conference on China Ordnance Society on Defence Technology, 2013: 48-52.

[10] 李伟, 王志刚. 双旋制导火箭弹运动特性分析 [J]. 固体火箭技术, 2014, 37(2): 143-149.

[11] 王志刚, 李伟. 滚转隔离结构制导火箭弹蒙特卡洛法仿真研究 [J]. 计算机仿真, 2012, 29(11): 99-103.

[12] 郝永平, 孟庆宇, 张嘉易. 固定翼二维弹道修正弹气动特性分析 [J]. 弹箭与制导学报, 2012, 32(3): 171-173.

[13] 张嘉易, 王广, 郝永平. 二维弹道修正弹鸭舵修正机构气动特性研究 [J]. 弹箭与制导学报, 2013, 33(2): 88-91.

[14] 纪秀玲, 王海鹏, 曾时明. 可旋转鸭舵对旋转弹丸纵向气动特性的影响 [J]. 北京理工大学学报, 2011, 31(3): 265-268.

[15] 韩子鹏. 弹箭外弹道学 [M]. 北京: 北京理工大学出版社, 2008: 150-153.

Analysis of Dynamic Equilibrium Angle and Ballistic Drift of Two-dimensional Trajectory Correction Projectiles with Fixed-canards

WANG Yi1,SONG Weidong1,SUN Yanqing2,LU Zhicai1

(1 Ordnance Engineering College of PLA, Shijiazhuang 050003, China; 2 The First Engineers Scientific Research Institute， General Armaments Department, Jiangsu Wuxi 214035, China)

The reverse roll of fixed-canards of two-dimensional trajectory correction projectiles will inevitably affect ballistic characteristics, including dynamic equilibrium angle and ballistic drift values. Characteristics analysis was presented in this paper. Assuming that fixed-canard has no pneumatic coupling with the shell, equation of the attack angle was proposed, which was suitable for all projectiles with dual spin configuration. Then analytic formulas of the dynamic equilibrium angle and ballistic drift were deduced. By studying the formula, the influence factors for the characteristics were analyzed. The conclusion shows that the overturn moment aerodynamic deviation coefficient most greatly affects the angle, and the roll velocity of the canard affects the characteristic slightly.

fixed-canards; trajectory correction; equation of attack angle; dynamic equilibrium angle; ballistic drift

2014-11-07

“十二五”武器装备预研基金资助

王毅(1986-),男,河南新郑人,博士研究生,研究方向:外弹道理论与应用。

TJ41

A