五种颗粒平均直径计算方法模拟研究

刘 仔,李艳臣

(1 哈尔滨工程大学航天与建筑工程学院,哈尔滨 150001;2 上海卫星装备研究所,上海 200240)



五种颗粒平均直径计算方法模拟研究

刘 仔1,李艳臣2

(1 哈尔滨工程大学航天与建筑工程学院,哈尔滨 150001;2 上海卫星装备研究所,上海 200240)

为了确定更加合理的颗粒平均直径计算方法,文中分别模拟研究了多尺寸分布与单尺寸分布的发动机内流场与性能参数的差异。采用高雷诺数条件下的k-ε湍流模型与颗粒轨道模型进行数值模拟。模拟结果表明,5种颗粒平均直径计算方法得到的单尺寸分布的计算结果与多尺寸分布的计算结果均存在偏差。采用质量平均法与体积表面积平均法求解颗粒平均直径较好,而线性平均法不宜采用。

颗粒轨道模型;质量平均法;体积表面积平均法;线性平均法

0 引言

两相流动在固体火箭发动机内普遍存在,研究发动机内的两相流场对发动机的合理设计具有重大的意义,因此国内外通过数值模拟对固体火箭发动机内的两相流场与发动机性能参数进行了大量的研究工作[1-6]。发动机中的颗粒存在粒径的颗粒数分布和粒径的颗粒质量分布两种多尺寸分布[7]。虽然多尺寸分布计算结果优于单尺寸分布计算结果[8],但是当采用多尺寸分布进行数值计算时,会导致计算机的计算量成倍增加,导致计算效率会降低,因此为了缩短计算机的计算时间,一般数值模拟中都采用单尺寸分布代替多尺寸分布。目前能够代替多颗粒的单颗粒直径计算方法有5种,研究5种方法中哪种方法计算得到的发动机性能与两相流场最接近多尺寸分布具有较大的工程实际意义。

1 数值计算方法

1.1 气相控制方程与湍流模型选择

气相控制方程的通用形式为:

(1)

其中:φ是任意独立变量;Γφ是输运系数;Sφ是气相源项;Spφ是气相与颗粒之间相互作用源项。在进行数值模拟过程中,文中选择RNGk-ε模型两方程湍流模型,采用标准壁面函数法对发动机壁面进行处理。

1.2 颗粒相控制方程

连续方程:

(2)

其中:A是发动机的通道面积;vkn是垂直于通道截面的颗粒分速度。

在i方向上的动量方程:

(3)

其中:τrk是颗粒相的动量弛豫时间;gi是重力加速度在i方向上的分量。

能量方程:

(4)

其中,在方程的右边分子中的第一项是颗粒与气相之间对流换热,而后一项是颗粒与气相之间的辐射换热。TR是辐射温度,εp是发射率,σ是玻尔兹曼常数,ck是颗粒的比热。

1.3 物理模型与边界条件

计算模型如图1所示。其中两相流中的颗粒相为Al2O3,气相为推进剂燃烧产生的燃气。Al2O3质量分数为25.0%,密度为3 960.0 kg/m3,比热为1 408.0 J/(kg·K);燃气的定压比热为1 811.0 J/(kg·K),相对原子质量为20.174,比热比k为1.226。其中入口a设定为质量流量入口,燃气与颗粒的质量流量为4.0 kg/s,颗粒与燃气的温度设定为3 200.0 K,壁面b设置为无滑移壁面,颗粒与壁面之间的作用设置为反弹,对称轴c设置为对称边界,出口d设置为压力出口。

图1 物理模型

2 算例验证

文中对文献[9]的数据进行模拟对比。图2给出了文中与文献中颗粒的分布对比,验证了文中计算方法的合理性与正确性。

图2 颗粒直径为3.90 μm时喷管中的无颗粒区对比

3 不同颗粒平均直径计算方法

其中对多颗粒进行求解平均直径计算方法有5种[7],包括线性平均法、表面积平均法、体积平均法、体积表面积平均法和质量平均法。选取平均直径计算方法的原则是按照颗粒平均直径计算所得的结果应该与按多尺寸分布计算所得的结果相近,因此需要根据具体问题合理的选择颗粒平均直径,下面给出5种颗粒平均半径计算方法的计算公式。

(5)

(6)

(7)

(8)

(9)

文中采用文献[7]中给出的某种多尺寸分布,其中多尺寸分布规律如表1。利用5种颗粒平均直径计算方法对该多尺寸分布进行平均直径的计算,其中得到的5种颗粒平均直径计算结果如表2。

表1 多尺寸分布

表2 不同计算方法的计算结果

4 计算结果分析

图3与图4给出了5种不同的单尺寸分布与多颗粒分布下发动机轴线上的气相马赫数与温度分布。由图3可知,发动机轴线上的气相马赫数在喷管收敛段之前5种方法得到的结果与多尺寸分布的结果基本一致,但在喷管的扩张段内气相马赫数存在偏差。因为在发动机扩张段内颗粒在轴线上的积聚数量相差较大,则颗粒对气相的膨胀抑制作用很强,同时颗粒对气相的对流换热作用也很强。5种平均直径计算方法得到的结果均偏大,其中线性平均法、表面积平均法、体积平均法、体积表面积平均法和质量平均法的计算结果偏差依次减小。由图4可知,在发动机燃烧室和喷管收敛段内5种计算方法得到的轴线气相温度基本一致,偏差较大的位置在喷管的扩张段内,其中5种方法的计算结果在喷管的扩张段均偏小。因为颗粒直径较大时颗粒的随流性差,向发动机轴线积聚的数量越多,对气相的传热量也越大。质量平均法计算结果与多尺寸分布结果最接近,其次是体积表面积平均法和体积平均法,线性平均计算结果偏差最大。通过气相马赫数与温度的比较分析得,5种方法中质量平均法计算效果更好,其次是体积表面积平均法,模拟效果最差的是线性平均法。

推力F是固体火箭发动机的主要性能参数[10]。表3给出了多尺寸分布与5种颗粒平均直径计算方法得到的发动机推力。由表3可知,多尺寸分布计算得到的推力介于体积表面积平均法与质量平均法之间,其中质量平均法的计算结果偏小,而体积表面积平均法的计算结果偏大,因此更好的颗粒平均直径值介于以上两种方法计算结果之间。可以对以上两种方法得到的平均直径进行求算术平均值能够使计算结果更加接近多尺寸分布结果。5种计算方法中线性平均法的计算结果偏差最大,因此对于计算发动机推力时一般不宜采用。

图4 发动机轴线气相温度

表3 单尺寸与多尺寸分布计算推力比较

推力系数Cf是表征喷管性能的参数[10],其中Cf=F/(PcAt)。表4给出了多尺寸分布与5种颗粒平均直径计算方法得到的发动机推力系数。由表4可知,多尺寸分布计算得到的推力系数介于体积表面积平均法与质量平均法之间,其中质量平均法的计算结果偏小,而体积表面积平均法的计算结果偏大,因此更好的颗粒平均直径大小介于以上两种方法计算结果之间。可以对以上两种方法得到的平均直径进行求算术平均值能够使计算结果更加接近多尺寸分布结果。5种计算方法中线性平均法的计算结果偏差最大,因此对于计算发动机推力系数时一般不宜采用。

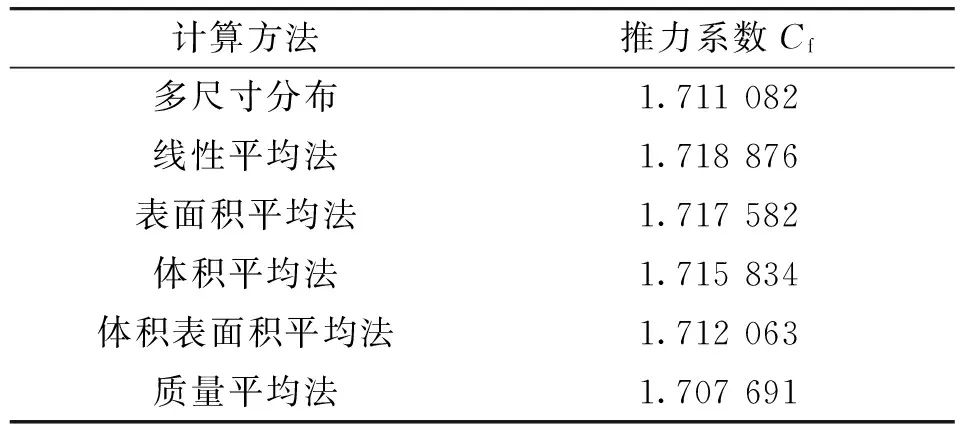
表4 单尺寸与多尺寸分布计算推力系数比较

5 结论

通过采用5种不同的单尺寸分布与多尺寸分布对固体火箭发动机内的两相流场进行模拟研究,得到了5种不同的单尺寸分布与多尺寸分布计算得到的发动机的内流场、推力与推力系数。模拟结果表明,发动机轴线上的气相马赫数与温度质量平均法的计算结果最接近多尺寸分布,其次是体积表面积平均法,偏差最大是线性平均法。多尺寸分布计算得到的发动机推力与推力系数均介于体积表面积平均法与质量平均法得到的单尺寸分布计算结果之间,质量平均法得到的结果均偏小,体积表面积平均法得到的结果均偏大,最好的平均直径值介于以上两种平均直径之间。其中线性平均法计算结果偏差最大,因此一般在计算发动机性能参数时不宜采用。

[1] Jun Sung Park, Seung, Wook Baek. Interaction of a moving shock wave with a two-phase reacting medium [J]. Heat and Mass Transfer, 2003, 46: 4717-4732.

[2] Sachdev J S, Groth C P T, Gottlieb J J. A parallel solution-adaptive scheme for predicting multi-phase core flows in solid propellant rocket motors [C]∥St. John’s Newfoundland, 13th Annual Conference of CFD Society of Canada, 2005.

[3] SH AFQ AT Wahab, XIE Kan, LIU Yu. Numerical simulation of multi-phase combustion flow in solid rocket motors with metalized propellant [J]. 航空动力学报, 2009, 24(7): 1654-1660.

[4] 贺征, 郜冶, 顾璇. 锥柱型装药固体火箭发动机两相内流场中颗粒运动的数值模拟 [J]. 宇航学报, 2005, 26(3): 354-357.

[5] 张志峰, 刘洋, 蔡体敏. 随机颗粒轨道模型在长尾喷管发动机流场计算中的应用 [J]. 固体火箭技术, 2007, 30(5): 376-380.

[6] 刘静, 徐旭. 随机轨道模型在喷管两相流计算中的应用 [J]. 固体火箭技术, 2006, 29(5): 333-353.

[7] 方丁酉. 两相流体力学 [M]. 长沙: 国防科技大学出版社, 1988: 1-68.

[8] 王增辉, 陈军涛, 陈林泉. Al2O3尺寸分布对喷管性能预示的影响研究 [J]. 弹箭与制导学报, 2008, 28(5): 142-144.

[9] 刘晓俐. 高金属含量固体火箭发动机的相关问题研究 [D]. 哈尔滨: 哈尔滨工程大学, 2006.

[10] 董师颜, 张兆良. 固体火箭发动机原理 [M]. 北京: 北京理工大学出版社, 1996.

LIU Zai1,LI Yanchen2

(1 College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, China; 2 Shanghai Institute of Spacecraft Equipment, Shanghai 200240, China)

To determine more reasonable calculation method for average particle diameter, the differences of internal flow field and performance of solid rocket motor in multi-size and sin gle-size distribution conditions were separately simulated. Numerical simulation usin gk-εturbulence under high Reynolds number and particle trajectory model was introduced. It shows that the results calculated by multi-size distribution are different from that of sin gle size distribution obtained through five calculation methods for average particle diameter. Mass average method and averaging method in volume and surface area are better to calculate particle average diameter, while linear average method should not be used.

particle trajectory model; mass average method; averaging method in volume and surface area; linear average method

2014-07-11

刘仔(1991-),男,四川邻水人,学士,研究方向:固体火箭发动机内的流动、传热与燃烧。

V435

A

Simulation Research of Five Average Particle Diameter Calculation Methods