基于发射车摇架的弹载捷联惯组标定方法

李光春,光星星,苏沛东,陈为海

(哈尔滨工程大学自动化学院,哈尔滨 150001)



基于发射车摇架的弹载捷联惯组标定方法

李光春,光星星,苏沛东,陈为海

(哈尔滨工程大学自动化学院,哈尔滨 150001)

基于发射车摇架,提出一种弹载捷联惯性组件标定方法。在摇架转动自由度范围内,引入发射车小横滚角,实现用5位置法惯组误差参数的全辨识,并用模方逼近法改进刻度因子的辨识,以保证标定精度。实验结果表明,改进后的标定方法,保证了弹体捷联惯组标定精度,降低了对高精度标定转台的依赖,为野外弹载惯组的日常维护提供了安全可信的方法。

捷联惯组;位置标定法;发射车摇架;横滚角;模方逼近

0 引言

捷联惯性组件在出厂前,首先会在实验室条件下对其标定,再将其安装在载体上。对于惯性组件,特别是安装在导弹上的惯性组件来说,随着战备时间的增加,惯性器件输出会发生变化[1],使得原有的标定结果对系统导航精度产生不利影响[2],因而对安装在导弹上的捷联惯组会定期对其进行维护。常规维护流程为:每隔一定时间,需要将惯组从弹体上拆下,重新在实验室利用高精度转台进行标定,根据标定结果修改惯组中的程序,将惯组重新安装到弹体上,即完成一次常规维护。在战备时期,甚至在战争中,当导弹等物资装备在指定位置就位后,不允许再进行拆卸;在野外也不可能有高精度转台可以用于标定;同时,多次拆装会引入安装误差。于是,提供一种直接利用摇架进行标定的方法,为野外设备上的捷联惯组的常规维护提供解决方法是有研究意义的。

在摇架上充分利用其的转动角度,用位置法标定,相较于速率法,更易于在野外条件下实现[3-4],但是,太多的位置编排对标定的便捷性会有一定的影响[5-7]。文中首先分析了现有基于导弹发射车摇架的标定方案,并通过可行性分析研究了该方案存在的缺陷;其次针对方案中不能辨识出的误差参数,提出车体小角度横滚角标定方案,并就其可行性进行了验证;最后,针对小角度横滚角测量误差较大问题,引入模方迭代逼近误差参数辨识法,并通过实验验证了该方案的可实现性,同时可在一定程度上避免多次拆装引入的安装误差,也为在导弹发射前的标定提供便捷方法,提高系统整体的机动性。

1 导弹发射摇架标定方案设计及可行性分析

1.1 捷联惯性组件误差模型

对光纤陀螺和石英挠性加速度计的误差模型来说,主要反映惯性组件使用时理想输入与实际输出的一种关系。车载弹体位置法标定时选择惯性组件的

简化静态误差模型:

(1)

式中:Ngx、Ngy、Ngz分别为三轴陀螺的实际输出;ωx、ωy、ωz分别为陀螺的理想输入;D0i、Kgi(i=x,y,z)分别为陀螺各轴的零位误差和刻度因子误差。

石英挠性加速度计简化后的静态误差模型为:

(2)

式中:Nax、Nay、Naz分别为三轴加速度计的实际输出;Ax、Ay、Az分别为加速度计的理想输入;A0i、Kai(i=x,y,z)分别为加速度计各轴的零位误差和刻度因子误差。

1.2 摇架标定方案

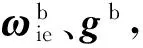
(3)

(4)

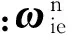
(5)

根据车载弹体摇架自由度及惯性组件误差模型,设计了5位置转位方案对惯性组件进行标定,其转位次序及每个位置上惯组各敏感轴输入如表1所示。其中,ωie=15.04 °/h为地球自转角速度、φ=45.066 7°为当地地理纬度、g=9.8 m/s2为当地重力加速度。

由惯组误差模型确定出每个位置上惯性组件的输入输出关系,可反映输出与对应的状态变量之间的观测性,观测性的优劣直接决定了误差辨识的成败。考虑到陀螺和加速度计在确定位置上输出是不随时间发生变化的确定值,可将其误差参数作为状态变量构建离散时不变系统,系统模型为:

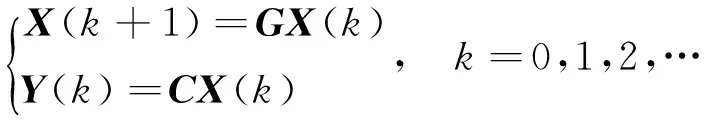
(6)

式中：X为n维状态,Y为q维输出,G和C为n×n和q×n的常值矩阵。对n维离散时间线性时不变系统,可观测判别矩阵为:

(7)

则系统完全能观测的充分必要条件为:

rank(QT)=n

(8)

由于系统为离散时不变系统,故陀螺和加速度计的状态矩阵Gg、Ga均选为单位对角阵;将需要辨识的误差参数选为状态变量,则对陀螺和加速度计分别为:

(9)

(10)

系统为离散时不变系统,其状态矩阵可选为:

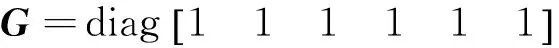
(11)

其观测矩阵则是与5位置输出所对应的输入激励:

(12)

式中：C11=C21=C31=C41=C51=I3×3

(13)

由表1,分别写出观测矩阵中的C15×3,将系统矩阵代入可观测性判别式得:rank(Qg)=6、rank(Qa)=5。

显然,对于陀螺仪,所选状态变量可以完全被观测,即利用5位置法设计的标定方案可以将其误差方程中所有误差参数全部激励;对于加速度计来说,状态变量不能完全被观测,即5位置法加速度计标定方案不能将加速度计误差模型中的误差参数全部激励,这一问题主要是由于俯仰轴方向上转台旋转自由度过小引起的。

1.3 标定方案可观测度分析

由上节分析可知,利用设计的5位置转位编排可以将陀螺状态变量全部辨识出来,但是对加速度计来说该种位置编排不可辨识出全部的误差参数。一方面,对于不同的状态变量,标定结果与所选惯性组件状态变量本身真实值之间的偏离程度有多大就无法进行评估,也即仅通过可观测性分析无法评定标定结果的可信性;另一方面,对于加速度计来说具体未被辨识的参数只通过可观测性分析也无法得到,所以引入可观测度分析,在对不同状态变量标定结果的可信性进行分析的同时,确定出该位置编排不能辨识出的加速度计误差参数。

设状态变量为X0,则在5位置上惯性组件量测值Z满足Z=QX0,此时对Q进行奇异值分解,得:Q=USVT,其中U=[u1,u2,…,um]T、V=[v1,v2,…,vn]都是正交矩阵,m和n为矩阵U和V列向量个数:

(14)

Λ=diag(σ1,σ2,…,σr)

(15)

式中σ1>σ2>…>σr>0为Q的奇异值。

由以上推导得:

(16)

经过分析求得每个状态变量值X0i对应的奇异值σi,σi为状态向量X0i中取得最大绝对值的状态所对应的奇异值。

由上式得出,X0i各值之间的大小关系可以直接通过Q的右奇异矩阵V的列向量计算得出,σi为与其对应的右奇异向量vi中取得最大绝对值的状态所对应的奇异值。对于陀螺来说,5位置上状态变量可观测度分析图如图1所示。纵坐标为每一状态变量的奇异值σi对应右奇异向量vi的大小,横坐标1～6分别对应D0x、D0y、D0z、Kgx、Kgy、Kgz这6个状态量,由图可知大小顺序为:Kgz、Kgx、Kgy、D0y、D0x、D0z;由图中对应状态变量的奇异值大小,可知每个变量的可观测度很高,也就说明该种位置编排最终的标定结果具有较高的可信度。同理,加速度计5位置状态变量的可观测度如图2,其大小顺序为:Kaz、Kax、A0y、A0x、A0z;从奇异值大小可以看出,对于可以辨识出的误差参数具有较高的可信度,Y轴加速度计的刻度因子无法辨识,这与可观测性分析结果一致。

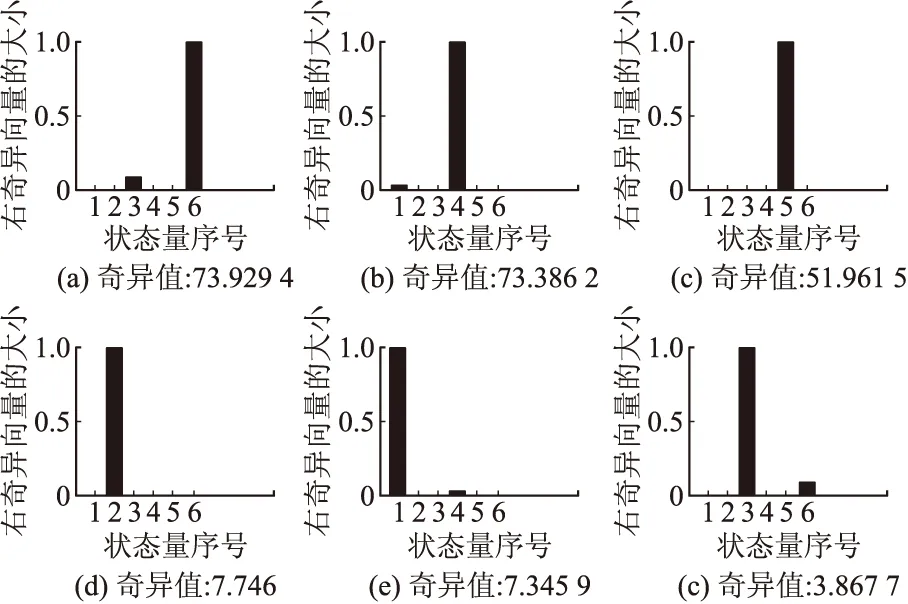
图1 陀螺误差参数可观测度分析图

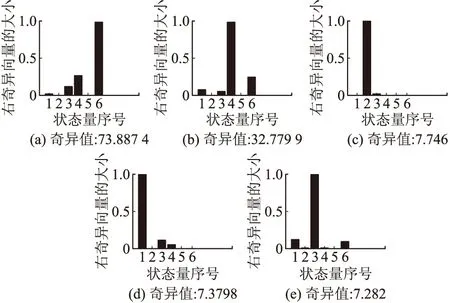
图2 加速度计误差参数可观测度分析图

1.4 惯性组件参数辨识

设弹体在俯仰方向上转动角度为β,则根据惯性器件误差模型及每一位置上输入输出关系,可分别得到陀螺和加速度计如下误差参数:

(17)

(18)

(19)

(20)

显然,对于陀螺和加速度计来说,误差参数辨识与其可行性分析相一致。

2 改进5位置标定方案及可行性分析

由上节分析可知,弹体安装于发射车以后,由于其摇架自由度限制,无法为Y轴加速度计的刻度因子提供输入激励,现有的摇架自由度使得其他的标定方案也都无法完成该误差参数的辨识[8]。为了能够实现Y轴加速度计刻度因子辨识,在保证整个弹体安全的前提下,利用发射车Y轴方向上小角度(横滚角γ)倾斜来为加速度计Y轴提供输入激励,实现该方向上刻度因子的辨识。

2.1 发射车改进5位置标定方案

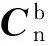
2.2 改进标定方案可行性分析

出于弹体安全等因素考虑,Y轴方向的横滚角一般需要取不大于10°,分析各轴的实际输入激励,再次利用上节选用的标定方案,对引入横滚角后新的摇架5位置标定方案进行分析。

(21)

取Y轴方向的小横滚角大小为10°,借助1.3节构建的离散时不变系统对系统进行可观测性分析。重新构建观测矩阵中的C15×3,利用系统可观测性判别式进行分析,则有:rank(Qg)=6、rank(Qa)=6,显然引入发射车小的横滚角后,无论是陀螺还是加速度计所选状态变量都可以完全被观测。同时,对改进方案进行可观测度分析。陀螺和加速度计的各个状态变量的可观测度分析如图3、图4所示,显然,改进后的标定方案能够实现惯性组件简化模型中所有误差参数的辨识,对陀螺来说,状态变量的可信度顺序为:Kgx、Kgz、Kgy、D0y、D0x、D0z,对加速度计来说,状态变量的其可信度顺序为:Kaz、Kax、Kay、A0x、A0z、A0y。

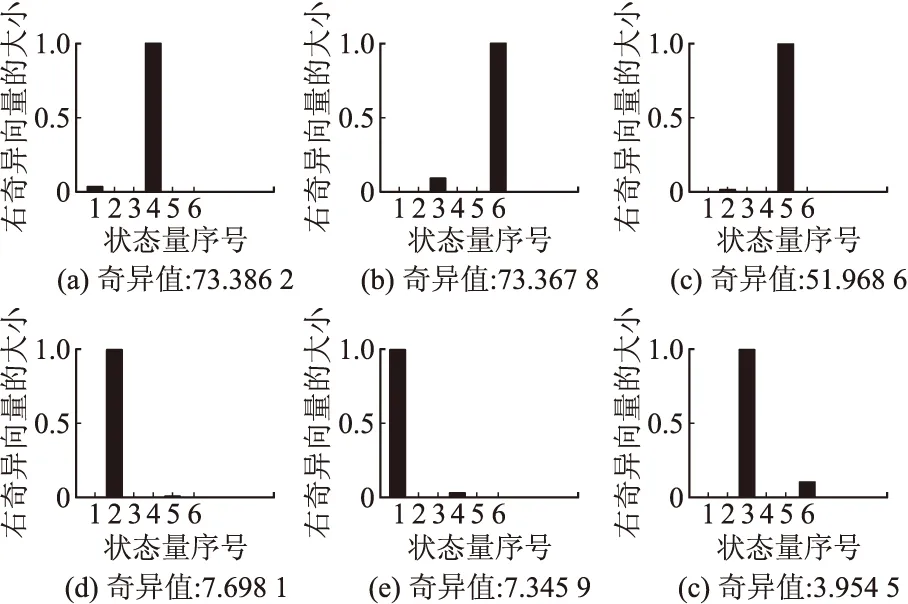
图3 改进后陀螺误差参数可观测度分析图

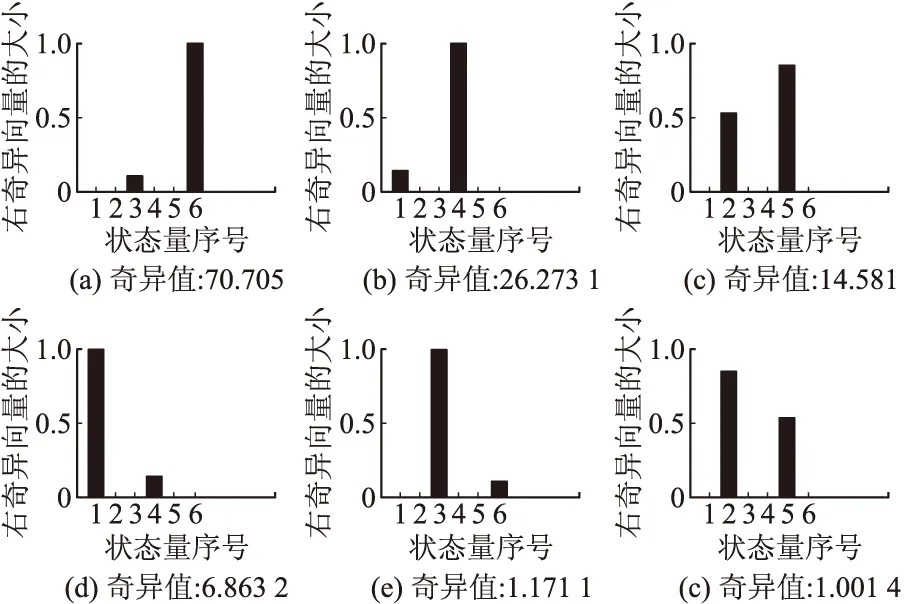
图4 改进后加速度计误差参数可观测度分析图

2.3 改进方案惯性组件参数辨识

经过2.2节分析可知,利用导弹发射车提供的横滚角可以增加惯性器件误差模型中参数的可观测性,即结合5位置法转位方案实现惯性组件模型中误差参数的辨识。对于陀螺来说,其辨识结果为:

(22)

同理,对于加速度计,有:

(23)

分析以上辨识结果可知,利用发射车提供横滚角可以实现惯性组件的误差参数的辨识。对于实际的导弹发射车,由于要控制导弹实现目标跟踪或者打击任务,俯仰和方位摇架的位置控制一般比较精确[9],所以在惯性组件误差参数辨识时可借助两个方向上的摇架转位来实现,但是该横滚角由发射车提供,且为不大于10°的角度,车载弹体角度测量比较困难。由式(22)～式(23)可知,如果角度测量出现大的误差,将导致标定结果的不准确。

3 改进参数辨识方案及结果验证

3.1 模方逼近法

经过分析改进方案后辨识出的惯组各个误差参数可知,各轴惯性器件的零偏的计算与其横滚角没有关系,即小横滚角测量的不准确只对器件的刻度因子辨识产生影响。

针对上述问题,文中用模方法来修正标定结果。模方迭代逼近法是通过模方法逐次迭代修正误差参数的一种参数辨识方法[10],由于在惯性器件激励提供时不需要精确知道实际的角度,逐次迭代就能逼近真实值。在5位置中选择3个位置组成3组无关的激励向量,利用逼近法只对陀螺及加速度计刻度因子进行辨识。

以加速度计为例分析。加速度计所敏感的是相对于惯性坐标系的比力,在运载体处于静止状态时,加速度计敏感的是重力加速度,惯组中3个轴上加速度计的理想输出必满足:

(24)

而由式(2)可以得到加速度的计算值为:

(25)

由于加速度计模型参数存在误差,加速度的计算值与理论值并不相等,依此建立误差模型为:

(26)

显然在误差最小时,加速度计的模型必然最准确,即各个模型参数达到最优。为得到最优的参数,

可以引入修正系数,对刻度因子加以修正,使得修正后的误差逐步接近于零。令刻度因子为:

(27)

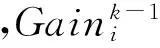
结合式(24)、式(26)和式(27),不考虑零偏部分,可得迭代方程:

(28)

3.2 惯组刻度因子辨识及标定结果验证

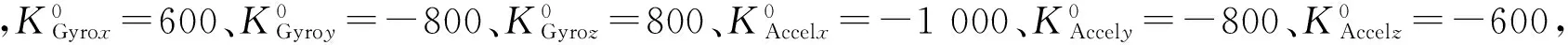
经过逐次迭代,可分别得到陀螺和加速度计刻度因子的调整系数Gain的变化如图5及图6所示。显然,对需要标定的刻度因子来说,经过5次迭代后,就完成刻度因子的辨识,且辨识速度很快。

经过直接计算及逼近法得到惯性组件误差参数,与同次开机的实验室高精度转台标定结果作对比,其惯组误差参数标定结果相对误差如表2所示。显然,这种方法能够很好的实现车载导弹捷联惯性组件的标定任务,保证良好的标定精度。

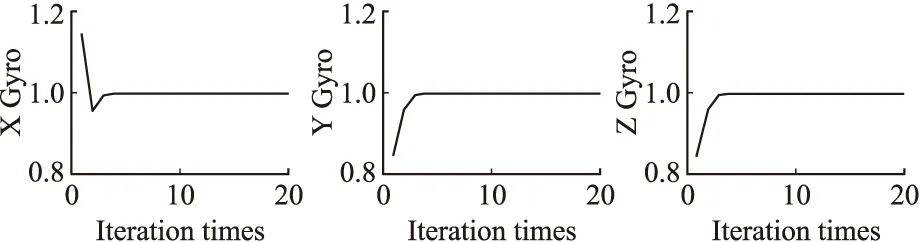
图5 三轴陀螺刻度因子调整系数Gain的变化图

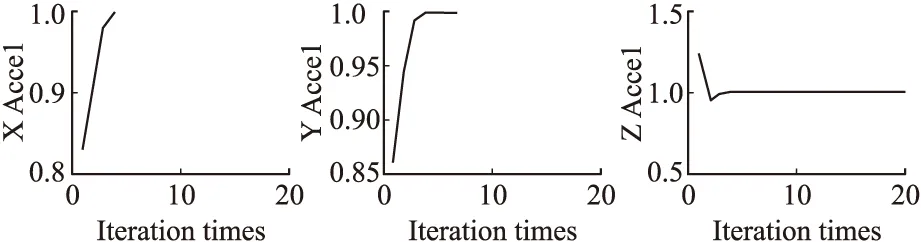
图6 三轴加速度计刻度因子调整系数Gain的变化图

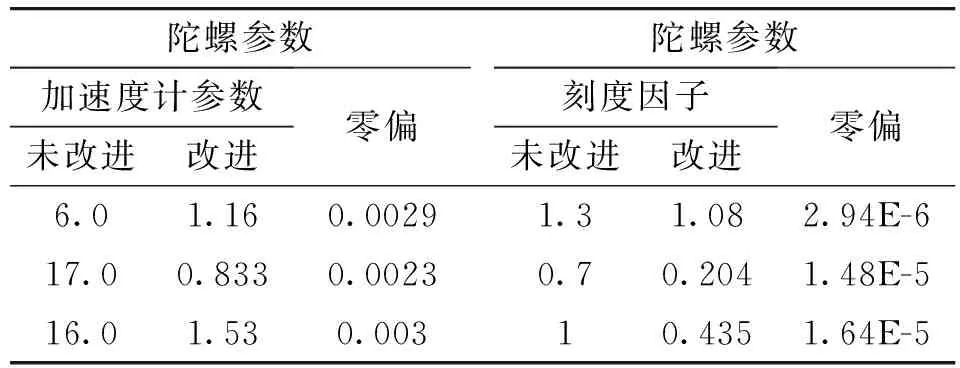
表2 惯组误差参数标定结果相对误差(%)

4 结论

文中提出了一种弹载惯组在架标定方案,借助导弹发射车提供小角度的横滚角,用5位置标定方案直接对惯组的零偏和刻度因子进行求解,并用模方逼近法对零偏进行修正。在实验室条件下模拟野外发射车摇架及横滚角,采集惯组的输出,完成误差参数的辨识,实验结果表明,改进后的标定方法,提高了弹载捷联惯组刻度因子的标定精度,整个标定方案极大的降低了标定过程对高精度标定转台的依赖,为野外弹载惯组的日常维护提供了一种便捷且安全可信的方法。

[1] LI C, ZHANG S F, CAO Y. One new onboard calibration scheme for gimbaled IMU [J]. Measurement, 2013,46(8): 2359-2375.

[2] 黄湘远, 汤霞清, 武萌, 等. 外场条件下战车捷联惯导系统原位快速多位置标定技术 [J]. 火炮发射与控制学报, 2014, 35(1): 65-70.

[3] LIU T, REN Q, WANG B, et al. An optimization method for self-calibration method of dual-axis rotational inertial navigation system [C]∥ The Proceeding of the 32nd Chinese Control Conference, 2013: 5198-5203.

[4] FU L, ZHU Y Q, WANG L L, et al. A D-optimal multi-position calibration method for dynamically tuned gyroscopes [J]. Chinese Journal of Aeronautics, 2011,24(2): 210-218

[5] 卿立, 李海强. 一种中低精度捷联惯测装置的不开箱标定方法研究 [J]. 中国惯性技术学报, 2004, 12(4): 16-19.

[6] 薛文超, 牟玉涛, 黄一, 等. 外场条件下激光捷联惯组多位置标定方法精度分析 [J]. 中国惯性技术学报, 2012, 20(1): 39-45.

[7] 孙伟, 徐爱功, 孙枫. 双轴旋转光纤捷联惯导八位置标定方法 [J]. 控制与决策, 2012, 27(12): 1085-1089

[8] FENG L, WANG B, DENG Z H, et al. On-line self-calibration for inertial platform system with a sin gle totally free axis [C]∥IEEE The 9th Asian Control Conference, 2013: 1-6.

[9] 游金川, 秦永元, 杨鹏翔. 制导弹箭捷联惯组在架标定方案研究 [J]. 传感技术学报, 2011, 24(7): 1001-1006.

[10] SEONG-HONG P W, FARID G. A triaxial accelerometer calibration method usin g a mathematical model [C]∥IEEE Transcation on Instruction and Measurement, 2010, 59(8): 2044-2053.

Research of Strapdown IMU Calibration Method Based on Missile Launching Vehicle’s Cradle

LI Guangchun,GUANG Xingxing,SU Peidong,CHEN Weihai

(College of Automation, Harbin Engineering University, Harbin 150001, China)

Based on launcher’s cradle, a calibration method was proposed about strapdown inertial measurement unit (SIMU) in vehicular missile. Within the limit of cradle’s rotational degree, and small roll of launch vehicle was introduced, 5-position was used for realization of IMU error parameters identification, and modular square approximation was used to improve calibration factor to ensure their accuracy. The experimental result shows that the improved calibration method provides a safe and reliable way for field IMU’s daily maintenance, meanwhile, calibration precision is ensured and dependence on high precision calibration turntable is reduced.

strapdown inertial measurement unit; position calibration; cradle of launching vehicle; roll angle; modular square approximation

2014-12-06

李光春(1967-),男,山东人,研究员,硕士,研究方向:惯性制导与控制。

TJ765.4

A