防空导弹毁伤目标六自由度建模研究
刘 恒,胡 铮,范利军
(63981部队,武汉 430300)
防空导弹毁伤目标六自由度建模研究
刘 恒,胡 铮,范利军
(63981部队,武汉 430300)
防空导弹毁伤目标的性能不断增强,传统基于质点的空中目标模型不能很真实的体现目标各项性能,跟踪效果不理想。针对这个问题提出一种基于刚体的六自由度模型。这种模型不仅具有三维的位置信息,还有三维的姿态变化信息,并根据空中目标的特点简化计算。仿真结果显示,这种方法有更高的跟踪精度和稳定性,且不易丢失目标,并能更好的体现目标各方面状态。
防空导弹;空中目标;刚体建模;目标跟踪;六自由度
0 引言
随着防空导弹所需要对付的空中目标复杂性和机动性不断增强[1],基于质点的跟踪控制(把目标视为只有三维平移运动的质点,不存在自身姿态变化)[2]已经不能很好达到控制效果。现实中的目标除三维平移运动以外,兼有3个姿态角的转动。基于刚体的跟踪控制可以实现精确稳定的跟踪目标,更为贴近真实情况。
建立模型的两个基本点是精确性和实用性[3],考虑控制目标的坐标位置和自身姿态六个自由度,精确性大幅度增强,但是会使系统复杂化,冗长的计算会降低跟踪控制的实时性,即实用性降低[4]。文中在结合这两方面的基础上,探索飞行目标六自由度精确模型的建立,简化计算的同时提升系统实用性。
1 坐标系定义
对于位置坐标来说,采用常用的惯性坐标系(inertial coordinate system)[5],即适用牛顿运动定律,坐标原点固定于大地,3个坐标轴(X,Y,Z)相互垂直,记为[x,y,z]T。
惯性坐标系规定了空中目标的位置信息,即3个自由度,而自身的姿态3个自由度利用体坐标系规定,如图1所示。3个坐标轴(Xb,Yb,Zb)相互垂直,θ、ψ和φ分别为俯仰角、偏航角和滚转角[6],(ibx,iby,ibz)为坐标单位向量。
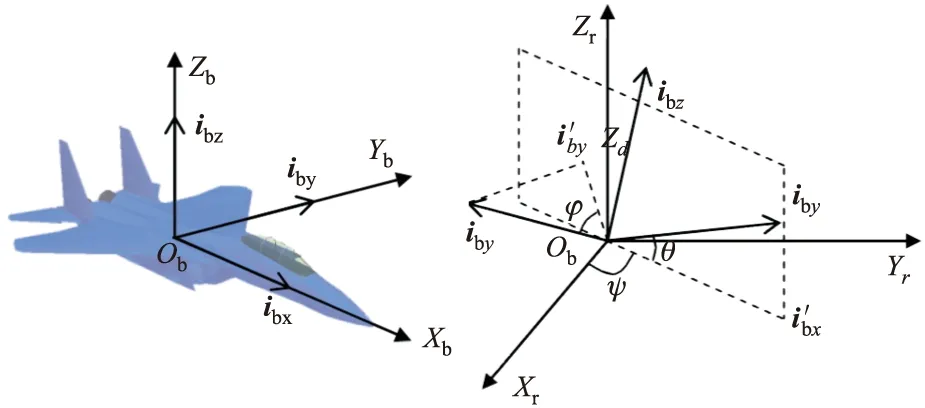
图1 空中目标体坐标系
2 空中目标的位置运动
空中目标的位置运动主要取决于作用于其上的合力f,其合力一般可分解为自身重力、发动机推力和空气动力[7]。
重力通常为固定值,记为G,垂直指向地心。
发动机推力矢量为W,为简化模型,定为始终固定于体坐标轴,与Xb同向。
空气动力记为fw,且有:
(1)
式中:D、C和E分别为空气的阻力、侧力和升力;CD、CC和CE为其无量纲系数;ρ为空气密度;v是目标速度;S为目标参考面积。
根据空中目标侧滑角小等特点[8],简化合力方程,在惯性坐标系上进行描述:
f=(Pbi)-1(Wib+Pbwaw)=
(2)
式中:α和β分别为空中目标的迎角和侧滑角,Pbi和Pbw为变换矩阵[9],且有:
3 空中目标的姿态运动
空中目标自身的姿态运动除外部影响外,主要是由本身的副翼控制,即由控制者的控制意图变换的,具有一定的智能性,不能用数学模型进行精确建模。结合模糊理论,简化模型,将空中目标姿态变化固定为3个模式:
A)匀速等高直线飞行
即空中目标控制者保持现有状态飞行。
B)纵向运动
即空中目标爬升或俯冲,俯仰角变化,偏航角和滚转角保持不变。
C)转弯运动
即空中目标协调转弯,俯仰角、偏航角和滚转角均有变化,且满足条件:侧滑角约为0,外部合力沿ibz方向[10]。
各模式下姿态角变化情况如表1所示。

表1 各模式姿态角
结合空中目标所受外力,有:
Ecosφ=mg
(3)
Esinφ=mωv
(4)
gtanφ=ωv⟹φ=arctan (ωv/g)
(5)
4 空中目标的综合运动
对目标在第k时刻的状态Xk建模,且有:
Xk=G(xk,yk,zk,vk,ψk,θk,φk,χ,ξk,ωk,Δθk,Tk)
(6)
其中:G是作用函数;vk是速度矢量;χ是空中目标类型参数;ξk为空中姿态变化模式(ξk∈{A,B,C});Tk是运行时间。在给定初始位置、姿态和速度条件下,变量{xk,yk,zk,vk,ψk,θk,φk}均为变量{χ,ξk,ω,Δθ,Tk}的函数,简化计算。下一时刻的状态Xk+1可以根据上一时刻状态Xk进行递推计算,其过程如图2所示。

图2 空中目标模型递推流程
进行递推计算前,确定控制目标的飞行状态是否发生了变化。如果没有变化,则加入一个小的扰动量。如果发生变化,则获取控制者的输入量,确定飞行模式,设定该模式参数,并进行状态积分,在给定初始条件的基础上利用控制者的输入量(ωk,Δθk,Tk),同时确定变换矩阵Pbw,在计算合力f后计算速度与位移,最后计算姿态角。
5 仿真实验
分别对基于质点和基于刚体的跟踪控制方法进行仿真验证。空中目标采用典型复合机动航行[11],3种姿态变换模式平滑连接,为了保证对两种建模方法进行验证,采用了传统的跟踪算法,未使用智能控制或卡尔曼滤波等,如图3所示,给定初始条件,由A模式开始,后面每一阶段的初始条件为上一阶段的输出。

图3 空中目标机动过程
分别对基于两种模型的控制方法的位置跟踪误差和速度跟踪误差进行对比。
如图4所示,图4(a)为位置均方差比较,图4(b)为速度均方差比较,无论空中目标在匀速飞行模式或机动转弯模式下,基于刚体跟踪方法的跟踪效果明显优于基于质点的跟踪方法(同时间幅度值比较)。在3个坐标方向,基于刚体的跟踪方法稳定性都很良好,峰值较小,在机动转弯时不易丢失目标,对跟踪精度和可靠性的提高非常明显。
但是由于计算量的增加,根据软件仿真结果显示,执行时间大约为基于质点的跟踪方法的600多倍,影响了该种方法的实时性,对跟踪硬件、运算能力提出了更高的要求。
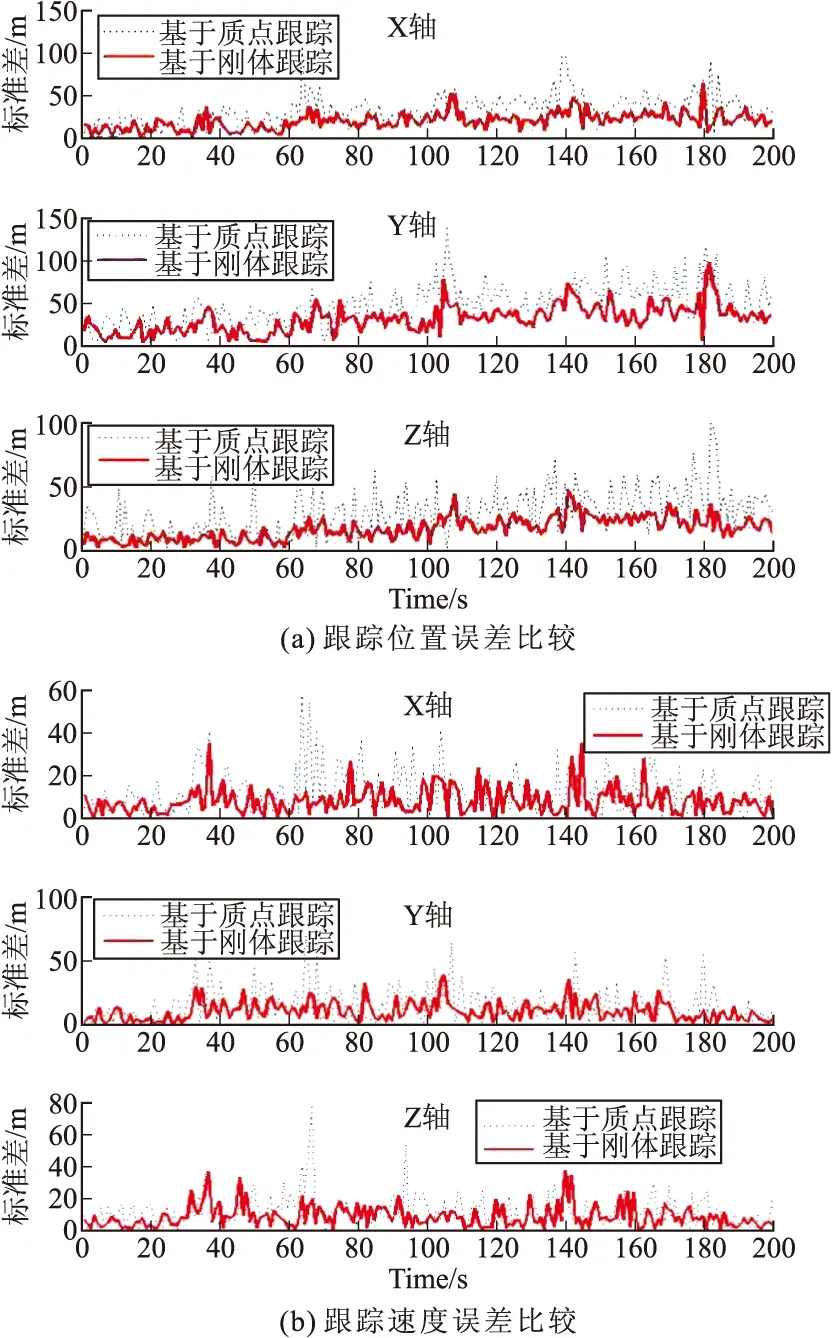
图4 跟踪均方差误差比较
6 结束语
文中提出基于刚体的防空导弹毁伤目标的六自由度模型建立方法。通过仿真实验对该跟踪方法进行了分析与验证,结果显示,相较于传统的基于质点的跟踪方法,基于刚体模型具有更高的跟踪精度和稳定性,特别在空中目标机动时,效果显著。但由于考虑因素增多,计算量不可避免地增加,延长了执行时间,降低了实时性,成为了主要瓶颈,也是以后的研究方向。
[1] 董文洪, 姜文志, 栗飞. 防空导弹武器系统对目标群射击效能分析 [J]. 现代防御技术, 2010, 38(2): 17-20.
[2] 陈良, 吴小俊, 王士同, 等. 一种新的常增益机动目标跟踪方法:α-β-γ-δ模型 [J]. 系统仿真学报, 2008, 20(17): 4550-4554.
[3] 王力, 钱林方, 高强, 等. 随动系统负载模拟器执行环节的建模研究 [J]. 南京理工大学学报, 2013, 37(4): 579-584.
[4] 周云锋. 基于刚体运动模型的机动目标跟踪算法研究 [D]. 石家庄: 军械工程学院, 2009.
[5] 阮晓钢, 侯旭阳, 龚道雄. 可重构旋翼无人飞行器的动力学建模与分析 [J]. 机器人, 2013, 35(2): 227-238.
[6] 杨阳, 崔金峰, 余毅. 三旋翼飞行器动力学分析及建模 [J]. 光学精密工程, 2013, 21(7): 1873-1880.
[7] 盛永智. 轨控直接力/气动力复合控制拦截弹的自动驾驶仪设计 [J]. 现代防御技术, 2009, 37(6): 51-54.
[8] 樊建鹏, 范红旗, 卢再奇. 基于高分辨率距离像的目标姿态角估计算法 [J]. 系统工程与电子技术, 2012, 34(12): 2413-2417.
[9] 李金梁, 曾勇虎, 周波, 等. 飞机目标静态与动态测量的姿态一致性 [J]. 北京航空航天大学学报, 2013, 39(4): 453-457.
[10] Ross K L. Coordinated flight [OL]. http: ∥www. friesian.com/flight.htm., 2001.
[11] 刘帅, 李俊山, 李智生. 空袭目标典型航迹模型的设计与仿真 [J]. 电光与控制, 2007, 14(4): 128-130.
Research on Mutilating Target Six Degree-of-freedom Modeling of Air-defense Missile
LIU Heng,HU Zheng,FAN Lijun
(No.63981 Unit, Wuhan 430300, China)
Target damaging performance of air-defense missile is growing. Traditional model of air targets based on particle can not reflect various performances of target, tracking effect are not ideal. In order to solve the problem, a six degrees-of-freedom model based on body has been proposed. This model has not only 3D position information, but also 3D attitude change information, and simplified calculation was achieved based on characteristics of air targets. The simulation results show that this approach has higher tracking accuracy and stability, not apt to lose goals, can better reflect target state.
air-defense missile; air targets; rigid body model; target tracking; six degrees of freedom
2014-12-07
刘恒(1990-),男,甘肃镇原人,工程师,研究方向:导弹装备电子设备检修。
TP15
A

