不同分子质量ETFE的非等温结晶动力学研究
李 星 王汉利 陈庆芬 赵 彬 王 平 牛 忠
(1.山东东岳高分子材料有限公司,山东 淄博 256401;2.东岳集团有限公司研究院,山东 淄博 256401;3.山东华夏神舟新材料有限公司,山东 淄博 256401)
不同分子质量ETFE的非等温结晶动力学研究
李 星1,2王汉利3陈庆芬1,2赵 彬3王 平3牛 忠3
(1.山东东岳高分子材料有限公司,山东 淄博 256401;2.东岳集团有限公司研究院,山东 淄博 256401;3.山东华夏神舟新材料有限公司,山东 淄博 256401)
采用差示扫描量热仪对乙烯-四氟乙烯共聚物(ETFE)进行了分析,利用经验公式求出了样品的重均分子质量,并用莫志深法和Kissinger法研究了其非等温结晶动力学过程。结果显示所选3批树脂的重均分子质量分别为1.72×106g/mol、7.46×105g/mol和3.14×105g/mol;莫志深法和Kissinger法适用于ETFE的非等温结晶动力学分析,得到了分子质量和相关结晶参数之间的关系,经计算,3批样品的结晶扩散活化能分别为512.43 kJ/mol 、698.50 kJ/mol 和1 079.01 kJ/mol。
乙烯-四氟乙烯共聚物;重均分子质量;非等温结晶动力学;结晶扩散活化能
0 前言
乙烯-四氟乙烯共聚物(ETFE,F40)具有优异的易加工性、化学稳定性、尺寸稳定性、介电性能、耐老化性和较高机械性能等特点[1],被广泛应用于化工防腐、大飞机和核反应堆用线缆、新型建筑膜材料等领域。
聚合物的非等温结晶行为更接近聚合物成型加工的实际过程,通过此方面的研究,可以了解温度场对聚合物结晶过程和结晶结构形态的影响[2]。占晓强、李亚东[3-4]利用Jeziorny法、莫志深法和Kissinger法研究了ETFE的非等温结晶动力学,结果显示莫志深法比较适用。目前还没有关于分子质量对ETFE非等温结晶过程的影响,为此,本文主要利用经验公式求出了3批ETFE样品的分子质量,并用莫志深法和Kissinger法研究了分子质量对其相关非等温结晶动力学参数之间的关系,有关结果对于研究生产工艺控制和树脂应用成型加工具有重要的指导意义。
1 实验部分
1.1 主要原料
ETFE(牌号DS401),山东华夏神舟新材料有限公司,熔融指数MFR(测试标准ASTM-D3159)分别为2 g/10 min、10 g/10 min和53 g/10 min的3种树脂。
1.2 主要设备和仪器
差示扫描量热仪(DSC),Q100,美国TA公司。
1.3 性能测试与结构表征
DSC分析:在高纯氮气保护下,分别将6 mg左右的4批测试样品,以10 K/min的速率从30 ℃升温至300 ℃,恒温5 min消除热历史,然后分别以5 K/min、10 K/min、15 K/min、20 K/min 、30 K/min的冷却速率降至室温。
2 结果与讨论
2.1 样品分子质量的测定
几乎很难找到适合ETFE的溶剂,文献报道[5]ETFE可以溶于290 ℃温度的己二酸二乙丁酯(DIBA)中,但经验证几乎不被溶解。因此,采用常规聚合物分子质量及分子质量分布测试方法,如分级法、超速离心法和凝胶渗透色谱法等难度很大。Tuminello[6]等建立了动态黏弹法测量ETFE分子质量及分子质量分布的新方法,但需要建立数学模型,利用最小二乘法进行求解。
工业上一般采用固定温度下测得的树脂熔体流动速率(MFR)作为衡量树脂分子质量的标准,MFR越大,分子质量越小。为了研究分子质量对结晶动力学的影响,选取了熔融指数为2 g/10 min、10 g/10 min和53 g/10 min的3批样品,编号分别为x、y、z。
根据分子质量Mw和MFR值的对应关系[7],由拟合得到如下经验关系式:
MFR=2.16×1012Mw-1.93
可得所选3种样品x、y、z的重均分子质量,分别为1.72×106、7.46×105和3.14×105。ETFE的缠结临界分子质量为1.26×106[6],x样品与此值比较接近,y和z样品都小于此值,因此,可以看作所选样品的分子质量都处于缠结临界分子质量以下,分子链相互之间几乎不发生缠结。
2.2 样品的绝对结晶度
求得绝对结晶度Xc,其中ΔHc是降温速率为20 K/min 时的熔融热焓,另外还有降温速率为20 K/min 时的相关参数,如起始结晶温度T0,终止结晶温度T∞,半结晶时间t1/2,具体如表1所示。
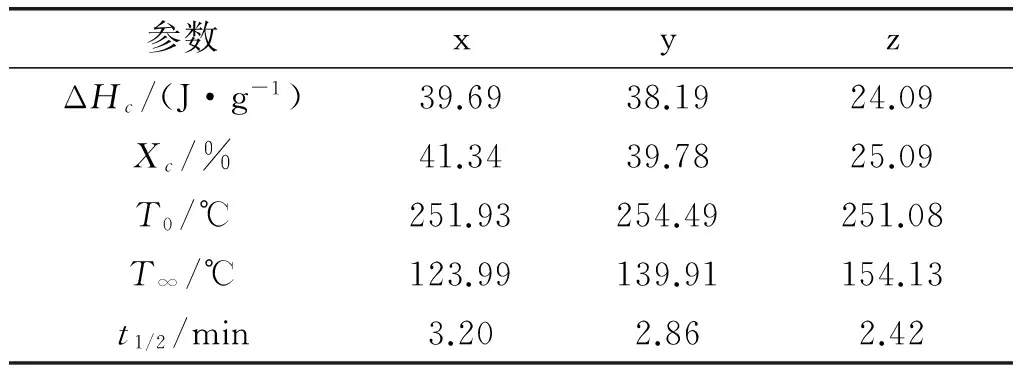
表1 降温速率为20 K/min时样品结晶过程的相关参数
由表1数据可以看出,绝对结晶度随着分子质量的减小而降低。所选的ETFE样品分子链为柔性链,且分子质量都处于缠结临界分子质量以下,不存在相互缠结问题,本身活动比较自由,容易进入晶格进行结晶,而较小分子质量样品由于生产工艺调整使得其链规整度下降,分子链进入晶格受阻导致结晶度变低。
半结晶时间随分子质量降低而减小,这可能是由于低分子质量聚合物起到了增塑作用,使得整体分子链链段活动能力增强引起的。
2.3 样品的非等温结晶动力学行为
2.3.1 样品的降温结晶曲线
图1为样品x、y和z在不同降温速率下的DSC曲线,由以下3张图分别得到其峰值温度Tp和半峰宽W1/2,如表2所示。
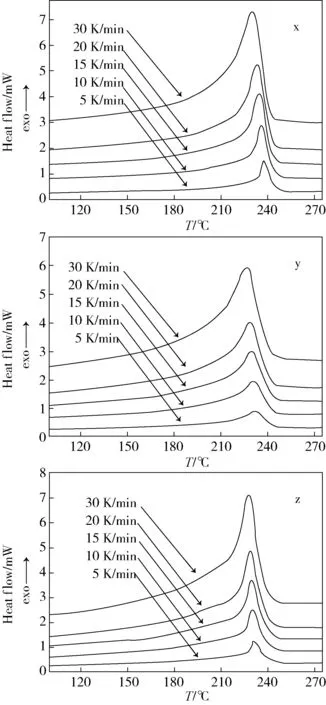
图1 3种样品在不同降温速率下的DSC结晶曲线表2 不同降温速率下3种样品的峰值温度和半峰宽
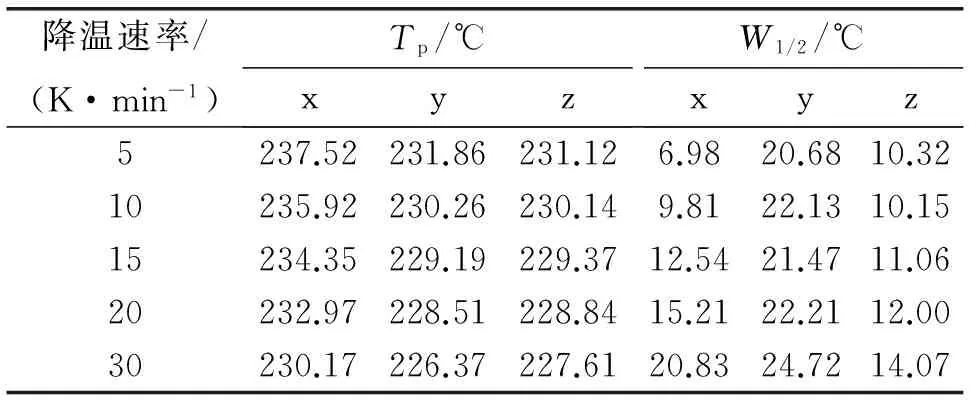
降温速率/(K·min-1)Tp/℃xyzW1/2/℃xyz5237.52231.86231.126.9820.6810.3210235.92230.26230.149.8122.1310.1515234.35229.19229.3712.5421.4711.0620232.97228.51228.8415.2122.2112.0030230.17226.37227.6120.8324.7214.07
从图1和表2可以看出,随着降温速率的增大,峰值温度Tp都向低温移动,且半峰宽W1/2都逐渐变大,这是因为聚合物分子重排进入晶格这一松弛过程需要一定的时间,聚合物分子链折叠进入晶格速率跟不上冷却速率,导致需要更大的过冷度才能结晶。另外,温度越低,分子链活动力越差,结晶越不完善,从而导致结晶半峰宽逐渐变大。
总体看来,分子质量大小对Tp和W1/2的影响没有特殊规律可循,这是由于除了分子质量外,分子质量分布、分子链规整度、树脂生产工艺等很多因素都会对聚合物结晶产生影响。而W1/2可以直接反映聚合物结晶的完善程度,可以从图1看到样品x结晶最完善,z次之,y结晶完善程度最差。
2.3.2 样品的相对结晶度变化过程
图2为样品x、y和z在不同降温速率下的相对结晶度与结晶时间的关系。
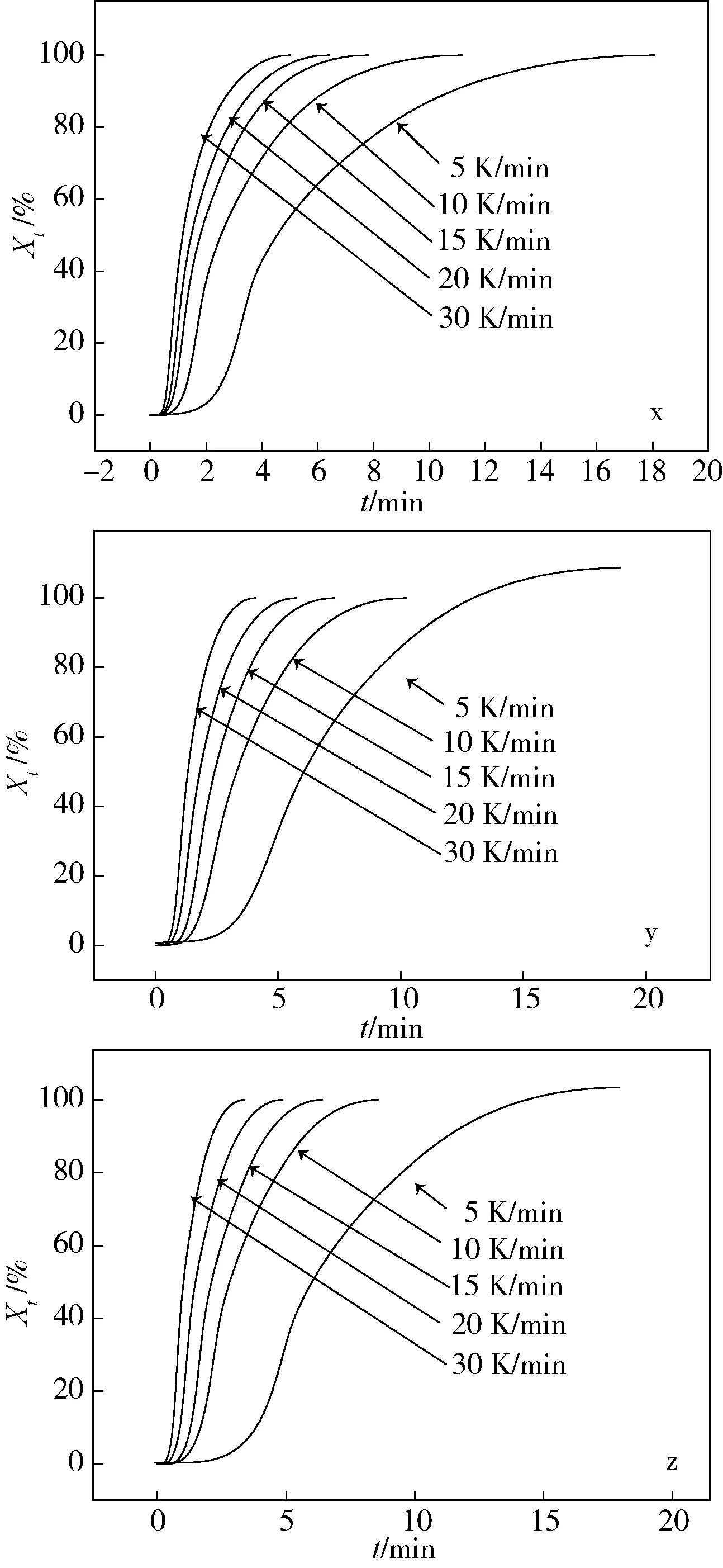
图2 3种样品不同降温速率下的相对结晶度随结晶时间的变化
从图2可以看出,3种样品的分子质量对其Xt~t曲线的趋势影响不大,都呈S型,表示了整体过程可以分为成核、球晶形成、球晶堆积3个不同的结晶阶段。第一阶段曲线斜率比较小,又称为结晶的诱导段,在该降温过程中逐渐形成结晶小晶核;第二阶段曲线斜率最大,为晶核放射性生长,形成球晶的阶段;第三阶段斜率变小,此时大多数球晶堆积在一起缓慢生长,而新结晶在其缝隙间生长成晶片。
2.4 莫志深法非等温结晶动力学分析
2.4.1 动力学参数的确定
在非等温结晶动力学过程中,任意结晶温度时的相对结晶度可由下式进行计算:
其中,T0为起始结晶温度,T为中间任意结晶温度,H为放热量,T∞为终止结晶温度。关于Xt的相关处理如下:Avrami法[9]被广泛用于非等温结晶动力学中,其方程为:
1-Xt=exp(-Zttn)
两边取自然对数,得到方程:
ln[-ln(1-Xt)]=lnZt+nlnt
其中,n为Avrami指数,与成核类型及生长尺寸有关,Zt是结晶速率常数,与成核及生长速率有关,t为结晶时间。
Ozawa法[10]把非等温结晶看作为一系列无穷小温区Avrami等温结晶过程的组合,其动力学关系为:
1-Xt=exp[-K(T)/φm]
对其两边取自然对数,得到方程:
ln[-ln(1-Xt)]=lnK(T)-mlnφ
其中,K(T)为温度T时非等温结晶的冷却函数,m为Ozawa指数,它与Avrami指数一样,与结晶机理有关,φ为冷却速率(K/min)。
莫志深法将Avrami方程和Ozawa方程综合[2],得到以下方程:
lnZt+nlnt=lnK(T)-mlnφ
变式得:
lnφ=(1/m)ln(K(T)/Zt)-(n/m)lnt
设定F(T)=[K(T)/Zt]l/m,a=n/m,则方程变式为:
lnφ=lnF(T)-alnt
F(T)的物理意义是单位时间内达到某一给定相对结晶度时应取的冷却速率值,其值越小,说明结晶体系本身的结晶速率越快。
2.4.2 非等温结晶动力学
在某一温度下,以lnφ对lnt作图得到一直线,由此可以得到两个参数:a和lnF(t),具体图形如图3所示,3种样品的具体参数如a、F(T)和相关系数r指标如表3所示。
由图3关系图及表3中的线性相关系数r值可以得知,莫志深法比较适合模拟ETFE的非等温结晶动力学过程。3种样品的a值基本为一个常数,且分子质量越大,a值越小,说明分子质量的变化会引起成核类型及生长尺寸等结晶机理的变化;F(T)随着相对结晶度的增大而逐渐增大,因为较大的冷却速率有利于结晶的快速形成,即单位时间内要想获得较高的结晶度,需要选择较快的冷却速率。
2.5 结晶扩散活化能
非等温结晶过程的结晶活化能通常采用Kissinger方程[11]来处理,因为它可以考虑到冷却速率对结晶过程中峰值温度的影响,方程如下:
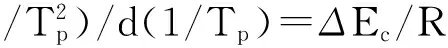
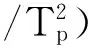
由图4关系图及表4中的相关系数r值可以得知线性相关性较高,用Kissinger方程求解ETFE的结晶扩散活化能比较适合。分子质量越低,活化能越高,这种现象与本文求解样品绝对结晶度部分所作的解释类似。由于生产工艺调整使得小分子质量样品分子链规整度下降,分子链进入晶格受阻,进而导致结晶需要的活化能较高。

图3 3种样品的lnφ~lnt关系图表3 3种样品的a、F(T)和线性相关系数r值

Xt/%axyzF/Txyzrxyz101.211.140.9215.2021.6417.86-0.9933-0.9973-0.9952201.231.130.9418.8726.1620.96-0.9937-0.9977-0.9963301.261.130.9522.3729.9223.22-0.9938-0.9983-0.9967401.291.130.9627.0834.2225.78-0.9951-0.9987-0.9966501.281.120.9633.7039.6529.43-0.9970-0.9993-0.9972601.281.120.9743.4546.5734.78-0.9983-0.9995-0.9974701.271.130.9956.1255.8441.79-0.9988-0.9996-0.9976801.281.131.0075.3867.5050.29-0.9988-0.9997-0.9979901.321.141.01113.3786.7462.83-0.9984-0.9998-0.9979

图4 3种样品的ln(φ的关系图表4 3种样品的结晶扩散活化能△Ec

xyz相关系数r0.97050.98070.9860ΔEc/(kJ·mol-1)512.43698.501079.01
3 结论
1)利用经验公式得到了3种样品的重均分子质量;
2)分子质量可以影响样品的绝对结晶度,但对结晶整体趋势不产生影响,结晶过程大体可以分为成核、球晶形成、球晶堆积3个不同的结晶阶段;
3)莫志深法应用于ETFE的非等温动力学过程,其中每个样品的a值基本为一个常数,分子质量越大,a值越小,而F(T)随着相对结晶度的增大而逐渐增大;
4)利用Kissinger方程求解了ETFE的结晶扩散活化能,结果显示分子质量越低,活化能越高。
[1]KerbowDL.InModernFluoropolymers:HighPerformancePolymersforDiverseApplications,ScheirsJ(ed) [M].NewYork:Wiley, 1997.
[2] 莫志深. 一种研究聚合物非等温结晶动力学的方法[J]. 高分子学报, 2008(7): 656-661.
[3] 占晓强, 包永忠, 黄志明, 等. 乙烯-四氟乙烯共聚物的非等温结晶行为[J]. 中国塑料, 2009, 23(12): 44-47.
[4] 李亚东, 强克刚, 李玉飞, 等. 火焰喷涂ETFE涂层的非等温结晶行为[J]. 高分子材料科学与工程, 2010, 26(5): 100-103.
[5]EnglishAD,GarzaOT.Compositionandmicrostructureoffluoropolymers.high-temperaturehigh-resolutionFT-NMR[J].Macromolecules, 1979, 12 (2): 351-353.
[6]TuminelloWH,BuckWH,KerbowDL.Rheologicalmolecularweightdistributiondeterminationsofethylene/tetrafluoroethylenecopolymers:implicationsforlong-chainbranching[J].Macromolecules, 1993, 26 (3): 499-503.
[7] 占晓强. 乙烯-四氟乙烯共聚物的结构与性能表征[D]. 杭州: 浙江大学, 2010: 21.
[8]NakafukuC,TakaokaK,KatsuraK.Meltingofethylene-tetrafluoroethylenecopolymer[J].PolymerJournal, 1999, 31(6): 557-559.
[9]JeziornyA.Parameterscharacterizingthekineticsofthenon-isothermalcrystallizationofpoly(ethyleneterephth-alate)determinedbyD.S.C[J].Polymer, 1978, 19(10): 1142-1144.
[10]OzawaT.Kineticsofnon-isothermalcrystallization[J].Polymer, 1971, 12(3): 150-158.
[11]KissingerHE.Reactionkineticsindifferentialthermalanalysis[J].AnalyticalChemistry, 1957, 29(11): 1702-1706.
Non-Isothermal Crystallization Behavior of Ethylene-Tetrafluoroethylene Copolymer with Different Weight-Average Molecular Weight
Li Xing1,2, Wang Hanli3, Chen Qingfen1,2, Zhao Bin3, Wang Ping3, Niu Zhong3
(1.Shandong Dongyue Polymer Material Co., Ltd., Zibo 256401, China; 2.Dongyue R&D Center of Dongyue Group Ltd., Zibo 256401, China; 3.Shandong Huaxia Shenzhou New Material Co., Ltd., Zibo 256401, China)
Ethylene-Tetrafluoroethylene copolymer (ETFE) was studied by DSC, weight-average molecular weight of samples were calculated by the empirical formula, DSC data was analyzed with Mo and Kissinger method. Results indicated that weight-average molecular weight of samples were 1.72×106, 7.46×105and 3.14×105g/mol, respectively; The Mo and Kissinger method could describe the non-isothermal crystallization process of ETFE very well, and the relationships between the weight-average molecular weight and the parameters were calculated; the crystalline diffusion activation energies of samples were 512.43, 698.50 and 1 079.01 kJ/mol.
ethylene-tetrafluoroethylene copolymer; weight-average molecular weight; nonisothermal crystallization kinetics; crystalline diffusion activation energy
李星(1984—),男,理学硕士,工程师,主要从事含氟高分子聚合物的研发工作。

