盾构近距离下穿引起已建地铁隧道纵向变形理论研究
张琼方 ,林存刚,丁 智,夏唐代 ,单华峰
(1. 浙江大学 软弱土与环境土工教育部重点实验室,浙江 杭州 310058;2. 浙江大学 滨海和城市岩土工程研究中心,浙江 杭州 310058;3. 宁波大学 建筑工程与环境学院,浙江 宁波 3152113;4. 浙江大学城市学院 土木工程系,浙江 杭州 310015)
1 引 言
盾构隧道在施工过程中不可避免地对周围土体产生挠动,当其近距离穿越既有隧道时会引起邻近隧道附加变形,而隧道在纵向的变形特性比较脆弱,过大的隧道纵向变形会导致隧道管片接缝过度张开而漏水或管片纵向受拉破坏。因此,研究隧道开挖条件下对邻近隧道的纵向变形性状具有重要的工程意义。
目前研究此类问题主要有4类方法:有限元模拟分析法、连续弹性分析方法、经验公式法和模型试验法。有限元方法[1]分析问题比较全面,但不可能对实际问题的每个需要研究的阶段都建立大型有限元模型进行长时间的分析。模型试验法[2]耗时长、试验繁琐、影响因素多,结果不易准确。连续弹性分析方法和经验公式法等下穿已建隧道的理论分析只适用于传统法对邻近隧道的影响,只考虑了土体损失对于已建隧道的影响[3-4],这种影响会使已建隧道下沉而非隆起,与盾构法开挖隧道的变形规律不同。经邵华等[5]和胡群芳等[6]分析工程实例发现,已建隧道在交叉穿越点产生隆起而非沉降,与盾构的推力、摩擦力和注浆压力有很大关系,这些力对已建隧道的影响不可忽视。
本文采用2阶段应力分析方法[7],第一阶段:利用 Mindlin理论解[8]计算隧道开挖等效荷载引起的已建隧道轴线处的附加应力,利用镜像法计算土体损失引起的已建隧道处的附加应力,并且与前者叠加;第二阶段:基于 Atwell等[9]提出的 Winker弹性地基梁模型,将已建隧道视为无限长梁,研究附加应力对已建隧道的变形影响。应用该方法对杭州市地铁4号线下穿地铁1号线进行了隧道变形的理论分析并与实测值相对比。
2 盾构掘进引起的附加应力分析
2.1 基本假定
本文假定:土体为均质,各向同性,半无限空间弹性体,泊松比为v,已建隧道视为无限长的Winkler弹性地基梁,如图1所示。刀盘附加推力q均匀作用于开挖面,作用面为与盾构直径相同的圆形,作用范围为盾尾后方单环管片宽度(m);盾壳摩擦力f沿盾壳均匀分布;同步注浆附加压力p沿盾尾圆周径向均匀分布,作用范围为盾尾后方单环管片宽度;盾构掘进仅为空间位置上的变化,不考虑时间效应;由于算得剪切应力较小,故忽略不计。

图1 盾构掘进模型Fig.1 The shield machine tunneling model
2.2 Mindlin解计算盾构参数引起的附加应力
林存刚[10]利用坐标转换求出了刀盘推力q、f、p作用下的土体中任一点(x,y,z)的附加应力,表达式较为简单清晰,可直接代入进行数值计算,这里列举其中的刀盘附加推力在点(x, y, z)引起的附加应力σzq表达式:
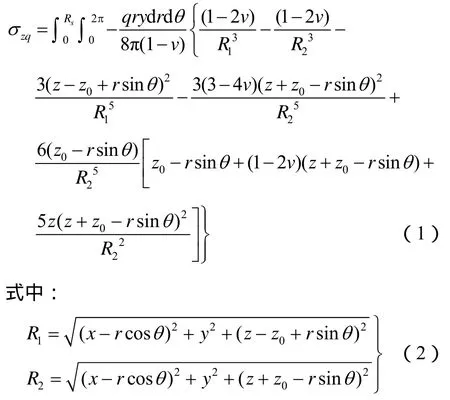
式中r、θ等意义见林存刚的研究[10]。
2.3 镜像法计算土体损失引起的附加应力
Lee等[11]研究得出盾构机盾构时落到土体底部,姜忻良等[12]提出盾构机移动模式为椭圆形非等量径向土体移动模式。本文采用盾构机落到底部的模式计算土体损失引起的附加应力。盾尾间隙作用下土体附加应力的计算见图 2(a)。对于任一微元大圆的坐标为(rcosθ,l,z0- (Rs-r)-rsinθ),可求其在P(x,y,z)处引起的附加应力。
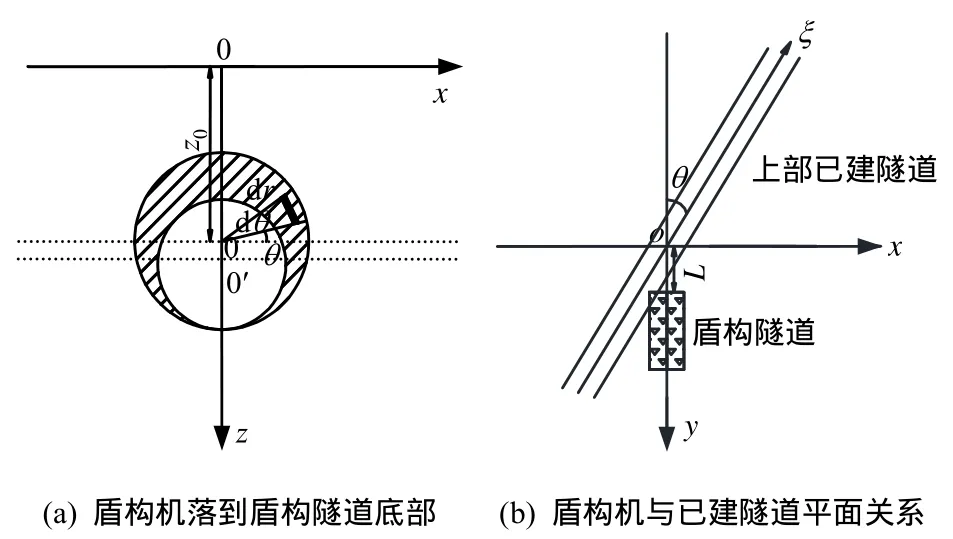
图2 盾构机落到盾构隧道底部和与已建隧道平面关系Fig.2 The shield machine is at bottom of existing tunnel and plane of existing tunnel and shield machine
对盾尾间隙内所有的微元引起的P点的附加应力叠加,即为盾尾间隙作用下P点总的附加应力。以z方向为例,所有盾尾间隙作用下σzloss的表达式为

式中:σzloss为z轴方向由土体损失引起的点(x,y,z)处的附加应力,计算方法采用齐静静等[13]的边界元法。
2.4 盾构推进引起隧道轴线处的附加应力
盾构掘进引起的隧道中轴线处的竖向附加应力为盾构正面推力、盾壳摩擦力、同步注浆压力产生的竖向附加应力的叠加,根据本文假设,剪切应力算出来的数值很小,可以忽略不计。盾构引起已建隧道竖向附加应力为

式中:σzq、σzf分别为刀盘附加推力和盾壳摩擦力在点(x,y,z)引起的附加应力。由于同步注浆压力是盾构机横截面径向的力,与所建坐标轴呈一定角度,故将其分解为两个方向:σzpv、σzph分别为竖直向、水平向同步注浆压力在点(x,y,z)引起的附加应力[10]。求得各应力分量后,即可应用 Winker地基梁理论计算已建隧道变形。
3 已建隧道纵向位移
当隧道附加作用广义荷载引起垂直于隧道的附加应力时,可以将隧道纵向看作是分布荷载下的Winker弹性地基无限长梁,隧道直径为D,则隧道与地层相互作用的力学方程可写为

式中:EI为隧道的抗弯刚度,附加分布荷载q(ξ)作用下的隧道,对于一点τ作用的集中荷载q(τ)dτ,该荷载引起隧道上任意点x的位移ds(τ)为

盾构机下穿已建隧道时要求解盾构机引起的已建隧道轴线处的附加应力产生的位移,可以进行坐标系转换。见图2(b)。已建隧道轴线与xyz坐标系中的x轴成一定的夹角,坐标转换得τ=x/sinθ,y=xt an23°+L,代入式(7),可得


式中:σ(x)为隧道中轴线处的附加应力。
4 工程实例分析
4.1 工程概况及参数取值
选取杭州市地铁4号线下穿地铁1号线,上下隧道平面投影夹角为 23°。隧道相对位置如图 2(b)所示。地铁4号线采用铰接型加泥式土压平衡盾构机,盾构外径为6.4 m。地铁4号线下穿地铁1号线的地层主要有第⑥1层黏土、第⑥2层质粉质黏土,土体泊松比v= 0.32。盾构直径2RS= 6.4 m,长L= 9 m,剪切模量G= 10 MPa;地铁4号线隧道轴线埋深z= 26.6 m,已建地铁一号线埋深z0=19.5 m,如图3所示。1号线已建隧道管片外径为6.2 m,内径为5.5 m,厚0.35 m,环宽1.2 m。隧道竖向位移采用徕卡 MS05AX全站仪进行自动化监测,监测范围为隧道交叉穿越点前后50 m范围。

图3 盾构隧道穿越已建隧道纵剖面图(单位:m)Fig.3 Longitudinal profile of shield tunnel position(unit: m)
附加应力式(4)中,各个参数的计算方法采用林存刚[10]的算法,取值:正面附加推力q= 200 kPa,盾壳摩擦力f= 150 kPa,盾尾同步注浆附加压力p=120 kPa。式(8)中隧道纵向刚度用叶飞[14]提供的方法取得 (EI)eq= 6 .676× 1 07kN⋅ m2。

4.2 已建隧道变形分析
从图4中可以看出,竖向变形分析即分析平面x′oz′内垂直于x轴的变形,只需代入σz用数值方法就可算出已建隧道变形。
本文通过改变已建隧道位置来改变盾构机与已建隧道相对位置。令式(8)中ξ= [-60, 60],ξ每个数间隔1.2 m,则可以求出交叉穿越点前后50 m已建隧道的变形情况,与监测到的数据进行对比分析。
(1)未穿越已建隧道竖向变形分析
当盾构机刀盘距交叉点10 m时,即图2(b)中L= 10 m,则可得到y=-xtan23°-10。

图4 已建隧道竖向与水平向变形平面Fig.4 Vertical and horizontal deformation plane of existing tunnel
从图5中可以看出,在盾构机穿越之前,刀盘附加推力,盾壳摩擦力和土体损失引起的已建隧道变形较大,而同步注浆压力的影响较小。各位移值叠加后计算结果显示盾构下穿越引起上部已建隧道变形与实测结果形态类似,但比实测结果略大。究其原因,盾构机和管片占据一定的空间,影响了附加应力的传递,导致理论值和实测值有差异。

图5 未穿越时已建隧道竖向变形Fig.5 Vertical deformation of existing tunnel before crossing
(2)穿越中已建隧道竖向变形分析
当盾构机刀盘位于已建隧道正下方时,即L=0 m,则可得到y= -xtan23°。从图6可以看出,此时盾壳摩擦力f引起已建隧道隆起,对隧道变形的影响最大,刀盘附加推力q也一定程度上影响了已建隧道变形,故在穿越中期应该对影响这两个参数的因素进行控制,如向盾构机注入泡沫或者润滑剂,降低土仓压力等,能达有效减小上部已建隧道隆起。理论计算结果和实际结果形态类似,实际值偏小,可能是由于盾构机盾构姿态等其他参数的影响。
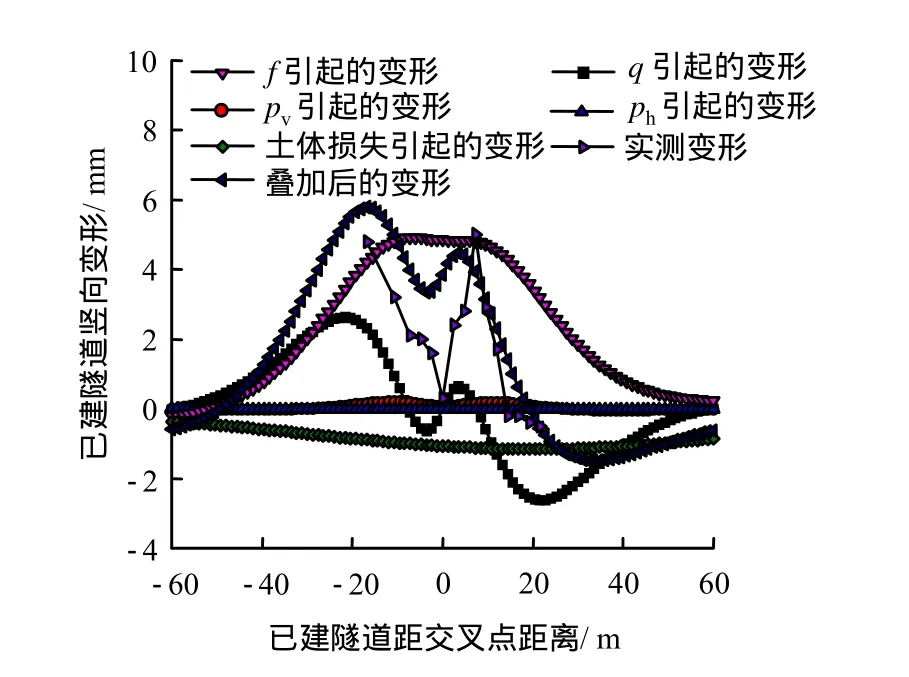
图6 盾构机即将穿越时已建隧道竖向变形Fig.6 Vertical deformation of existing tunnel during crossing process
(3)已穿越已建隧道竖向变形分析
当盾构机刀盘距交叉点10 m时,即L= -10 m,则可得到y= -xtan23°+ 10。
随着盾构机远离上部已建隧道下方,盾构参数刀盘附加推力q和盾壳摩擦力f和同步注浆压力都对土体产生拉力,而土体这种介质无法传递很大的拉力,故不计算盾构参数引起的附加应力,直接计算土体损失引起的变形如图7所示。以上结果与实际变形规律相差较大,原因可能是由于弹性解求出来是瞬时的解,忽略了时间效应,已建隧道的变形与周围土体相互作用,不可能瞬时变化,与本文中的假设有较大关系。

图7 盾构机穿越过已建隧道后竖向变形Fig.7 Vertical deformation of existing tunnel after crossing
5 结 论
(1)Mindlin解积分求取刀盘附加推力,盾壳摩擦力及同步注浆压力作用下的已建隧道附加应力与镜像法计算得出的地层损失引起的附加应力相叠加,结合Winker地基梁理论可以在未穿越、穿越中的工况下合理的预估盾构掘进引起的隧道位移。
(2)本文方法理论上具有很大的优越性,无论盾构隧道与已建隧道处于何种位置关系都能够计算已建隧道在任意方向的变形,是由于附加应力是三维空间下所求得的,而此处的Winker地基梁可以在任意平面内变化,故这种方法使用比较灵活。
(3)计算盾构的4个参数引起已建隧道变形,可对盾构不同状态下各个参数所引起的已建隧道变形的形态有所了解,合理控制影响4个参数的因素,即可减小已建隧道变形。
[1] 李磊, 张孟喜, 吴惠明, 等. 近距离多线叠交盾构施工对既有隧道变形的影响研究[J]. 岩土工程学报, 2014,36(6): 1036-1043.LI Lei, ZHANG Meng-xi, WU Hui-ming, et al. Influence of short-distance multi-line overlapped shield tunnelling on deformation of existing tunnels[J]. Chinese Journal of Geotechnical Engineering, 2014, 36(6): 1036-1043.
[2] KIM S H, BURD H J, MILLIGAN G W E. Model testing of closely spaced tunnels in clay[J]. Geotechnique, 1998,48(3): 375-388.
[3] NG C W W, BOONYARAK T, MAŠÍN D. Threedimensional centrifuge and numerical modeling of the interaction between perpendicularly crossing tunnels[J].Canadian Geotechnical Journal, 2013, 50(9): 935-946.
[4] 张治国, 黄茂松, 王卫东. 层状地基中隧道开挖对临近既有隧道的影响分析[J]. 岩土工程学报, 2009, 31(4):600-608.ZHANG Zhi-guo,HUANG Mao-song,WANG Wei-dong.Response analysis of existing tunnels due to adjacent tunnelling in multi-layered soils[J]. Chinese Journal of Geotechnical Engineering, 2009, 31(4): 600-608.
[5] 邵华, 张子新. 盾构近距离穿越施工对已运营隧道的扰动影响分析[J]. 岩土力学, 2004, 25(增刊 1): 545-549.SHAO Hua, ZHANG Zi-zin. Analysis of disturbing effect on running subway caused by adjacent shield driven[J].Rock and Soil Mechanics, 2004, 25(Supp.1): 545-549.
[6] 胡群芳, 黄宏伟. 盾构下穿越已运营隧道施工监测与技术分析[J]. 岩土工程学报, 2006, 28(1): 42-47.HU Qun-fang, HUANG Hong-wei. Analysis and monitoring on shield tunneling under existing adjacent tunnel[J]. Chinese Journal of Geotechnical Engineering,2006, 28(1): 42-47.
[7] 陈郁, 李永盛. 基坑开挖卸荷引起下卧隧道隆起的计算方法[J]. 地下空间与工程学报, 2005, 1(1): 91-94.CHEN Yu, LI Yong-sheng. Calculation of tunnel heaving due to unloading of pit excavation[J]. Chinese Journal of Underground Space and Engineering, 2005, 1(1): 91-94.
[8] MINDLIN R D. Force at a point in the interior of a semi-infinitesolid[J]. Journal of Applied Physics, 1936,7(5): 195-202.
[9] ATTEWELL P B, YEATES J, SELBY A R. Soil movements induced by tunnelling and their effects on pipelines and structures[M]. London: Blackie and Son Ltd., 1986.
[10] 林存刚. 盾构掘进地面隆陷及潮汐作用江底盾构隧道性状研究[D]. 杭州: 浙江大学, 2014.
[11] LEE K M, ROWE R K, LO K Y. Subsidence owing to tunneling: estimating the gap parameter[J]. Canadian Geotechnical Journal, 1992, 29(6): 929-940.
[12] 姜忻良, 赵志民. 镜像法在隧道施工土体位移计算中的应用[J]. 哈尔滨工业大学学报, 2005, 27(6): 801-803.JIANG Xin-liang, ZHAO Zhi-ming. Appfication of image method in calculating tunneling-induced soil displacement[J].Journal of Harbin Institute of Technology, 2005, 37(6):801-803.
[13] 齐静静, 徐日庆, 魏纲, 等. 隧道盾构法施工引起周围土体附加应力分析[J]. 岩土力学, 2008, 29(2): 529-544.QI Jing-jing, XU Ri-qing, WEI Gang, et al. Analysis of superimposed stress of surrounding soil due to shield tunneling[J]. Rock and Soil Mechanics, 2008, 29(2): 529-544.
[14] 叶飞, 何川, 朱合华, 等. 考虑横向性能的盾构隧道纵向等效刚度分析[J]. 岩土工程学报, 2011, 33(12): 1870-1876.YE Fei, HE Chuang, ZHU He-hua, et al. Longitudinal equivalent rigidity analysis of shield tunnel considering transverse characteristics[J]. Chinese Journal of Geotechnical Engineering, 2011, 33(12): 1870-1876.
[15] 仲锁庆, 张西平, 潘海利. 地基土基床系数研究[J]. 地下空间与工程学报, 2005, 1(7): 1109-1112.ZHONG Suo-qing, ZHANG XI-ping, PAN Hai-li. Study on foundation soil coefficient of subgrade reaction[J].Chinese Journal of Underground Space and Engineering, 2005, 1(7): 1109-1112.

