考虑颗粒棱角影响的直剪试验的离散元模拟

赵仕威，周小文，刘文辉，刘 攀

（华南理工大学 亚热带建筑科学国家重点实验室，广东 广州 510640）

1 引 言

颗粒材料的宏细观力学行为越来越受研究者们的关注。自 Cundall 等[1]提出并发展离散元理论以来，离散元方法逐渐成为学者们探索颗粒材料细观力学行为的强有力的数值工具。目前国内外学者采用离散单元法在模拟直剪试验和三轴试验等方面做了大量的工作，认为颗粒材料内部组构对宏观强度和变形有很大的影响[2-8]，特别地，颗粒形状的影响更为直接。

由于多边形[5]、椭圆[9]以及圆盘的 clump体[8]的形状简单、计算量小，在二维研究中经常被使用。这类研究虽然能够获得有益的结果，但局限于二维情况。为了更好地反映颗粒形状的影响，三维离散元方法越来越受到关注，多数针对椭球[10]、球体的clump体[2，4]进行研究。椭球主要用于研究长细比的影响，而球体的clump体可以有复杂的形状，除了用于研究长细比影响外，还可以研究如粗糙度、棱角度等的影响。对于一些真实颗粒，随着粒径的减小，颗粒形状趋于球形，此时颗粒形状差异主要体现在颗粒粗糙度或棱角度。多面体颗粒能够更好地反映真实颗粒（如砂粒）的棱角性，然而针对颗粒棱角影响的研究还比较少。

直剪试验具有简便易操作的优点，用其获得的强度指标具有一定的参考价值，很多学者在离散元模拟中选择直剪试验。本文通过修改三维离散元开源程序YADE[11]，建立相应的多面体离散元模型，尝试探究颗粒棱角度变化对颗粒材料直剪强度和变形的影响。

2 离散元模型

2.1 控制方程

离散元方法（DEM）可以用来计算颗粒系统中大量颗粒的运动（平移和转动）。通常，每个颗粒的运动是通过显示时步方法进行计算。在每个时步，力-位移定律（接触本构）和运动定律（牛顿第二定律）分别用来计算颗粒的接触力和颗粒的运动。质量为mi惯性矩为Ii的颗粒i的运动控制方程为

式中：vi、ωi分别为颗粒的平动速度和角速度；ni为该颗粒与周围颗粒的接触个数；α为阻尼系数，用来消散系统能量，以便颗粒系统在合理次数的迭代后达到稳定状态。如图1所示，作用在颗粒上的力包括重力mi g和接触力。接触力包括颗粒间的排斥力Fij和力矩Mij。当Fij与vi（或Mij与ωi）同向时，以上等式中α前的符号取负，反之取正。

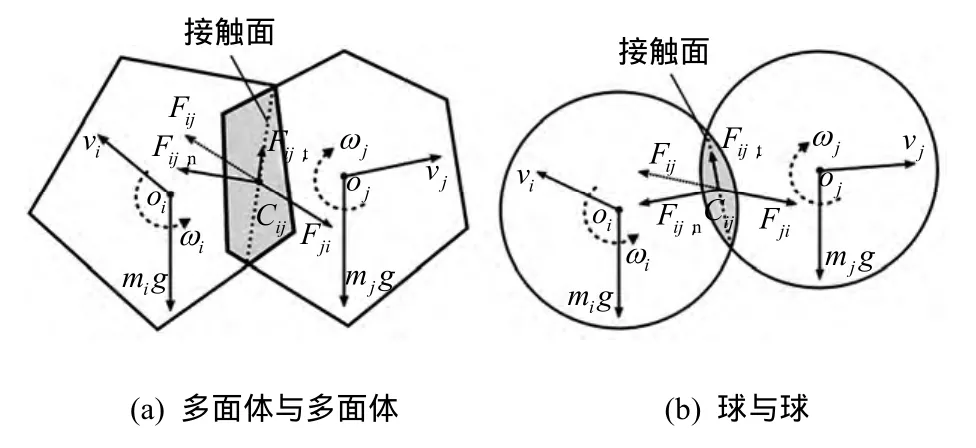
图1 两颗粒间相互作用二维示意图Fig.1 2D sketches of interaction between two particles

2.2 接触本构

在离散元方法中线弹性模型是最为简单和常见的接触模型，大多数离散元程序中法向接触力Fn通过式（3）获取。

式中：δ为颗粒间嵌入深度；Kn为法向线刚度。

本文采用一种更为直观并且可针对任意形状的法向接触模型[12－13]为：

式中：vc为颗粒间的重叠体积；Kn为法向体刚度。

颗粒间的重叠见图 1，图中夸大了颗粒间的重叠区域，体积需针对具体颗粒形状进行计算。球形颗粒间的重叠体积为

式中：ri、rj分别为颗粒i、j的半径；hi、hj分别为颗粒i、j对应的球缺高。

两个凸多面体间的重叠部分可采用对偶变换法[13－14]求得。

球形颗粒间的接触面（见图 1）为两者相交线构成的平面，而多面体颗粒间的相交线不一定共面，此时的接触面通过相交线的最小二乘拟合获取。法向接触力的方向为垂直接触面指向颗粒自身一侧。

切向接触力Fs按照常规方法计算由式（6）给出，方向为切向位移方向。

式中：Ks为切向刚度；Δu为切向位移。

库仑准则式（7）用于判断颗粒间是否产生滑动。一旦式（7）不成立，则产生滑动，此后需维持切向接触力μFn：

式中：μ为摩擦系数。

3 数值直剪试验

3.1 颗粒生成

颗粒形状采用顶点均匀分布在球面的理想凸多面体，如图2所示。这种颗粒形状的优点是可以有效地控制细长比和偏心率的影响，便于单独研究颗粒棱角度的影响。

图2 具有不同棱角的颗粒形状Fig.2 Particle shapes with different angularity

颗粒的生成算法简要描述如下：首先，在球面上随机产生n个点，并假设这些点之间存在一种与距离平方成反比的作用力。然后，不断调整这些点在球面上的位置，直至它们都达到相对平衡的状态。最后，以这n个点作为凸多面体的顶点，利用凸包算法即可求得相应的凸多面体。

3.2 试样生成

图 3为数值试样的制备流程。具体步骤为：① 在立方体容器中随机生成不重叠的单粒径球形颗粒，并在5倍重力加速度下自由沉积直到稳定见图 3（a）。② 在每个球形颗粒的位置生成方向随机的多面体颗粒，并移除球形颗粒见图3（b）。由于球形颗粒与多面体颗粒的外接球等大小，生成的多面体颗粒间不会出现重叠。③ 让多面体颗粒在5倍重力加速度下自由沉积见图3（c）。④ 当堆积体达到相对稳定状态后，撤去重力，并在堆积体上下面各加一块加载板。⑤ 让上板以一足够小的竖向速率向下移动直到与堆积体上部颗粒完全贴合。⑥ 上下板以相同的足够小的速率相向移动，从而实现对试样的单向压缩固结见图3（d）。

图3 试样制备流程Fig.3 Flowchart of specimen generation

在压缩过程中需要采用伺服机制让上下板上的竖向力保持为目标固结压力（如25 kPa）不变。固结过程持续到试样体积不再变化，见图3（e）。图3（f）为25 kPa固结压力下生成的试样。下一级固结压力（如50 kPa）下的试样可在此试样的基础上改变加载板上的目标固结压力继续压缩固结得到。

按照上述试样生成方法，本文选取4种颗粒形状，见表 1，表中颗粒棱角度定义为球度与顶点数的比值）生成对应的4种不同颗粒棱角度的试样。每组试样由1 000个相同形状的单粒径颗粒组成；各组试样的颗粒体积相等。图4为在25 kPa固结压力下生成的4种不同棱角度的颗粒试样。

表1 颗粒形状几何参数Table 1 Shape parameters of particles

图4 4种不同棱角度的颗粒试样Fig.4 Four specimens with different angularities

3.3 直剪试验

数值试验直剪仪（长×高×宽）为50 mm×50 mm×15 mm，由8面刚性墙构成，如图5所示。在剪切前，试样在一定竖向压力下压缩固结到体积不变。在剪切过程中，固定下盒不动，上盒以一定的剪切速率沿长度方向对试样进行剪切；同时，上盒顶板需要实时调整竖向位置，以保持作用在上面的竖向力不变。试样的体应变通过顶板位置确定；剪切应力（由于本文不计剪切盒与颗粒间的摩擦）通过下盒左右两块刚性墙上的力计算。

图5 剪切盒示意图Fig.5 Sketch of direct shear box

通常，实验室的直剪试验剪切速率很小，以3 mm/min 的剪切速率为例，达到13%的剪应变需要130 s。假设DEM中的计算时步为2.5×10－7s，到达相同的剪应变需要5.2×108时步。在CPU计算能力为1 h每1 s的模拟时间（4.0×106时步）的情况下，需要 130 h的实际时间完成 13%剪应变的模拟，显然不具有实际操作性。本文采用较大的剪切速率2.5×10－4mm每时步，在26 000次迭代后剪应变达到 13%，有效地缩短了程序运行时间，获得的结果也是可接受的。

离散元模拟的一些主要参数见表 2。表中，颗粒大小指与颗粒具有相等体积的球体半径；颗粒密度和摩擦系数参考砂和碎石的密度和摩擦系数；阻尼系数和材料刚度按经验取值。需要说明的是，所有试样是在0重力场下进行剪切。

表2 DEM模拟中的颗粒参数Table 2 Particle parameters by discrete element method simulation

4 结果与讨论

4.1 宏观强度与变形

剪切前对 4种不同颗粒棱角度的试样进行固结，固结后相应的孔隙率见表 3。对于同一种颗粒棱角度的试样，竖向固结压力越大，固结后试样越密实；在同一竖向固结压力下颗粒棱角度越小，颗粒形状越趋于球形，固结后的试样越松散，但相应孔隙率相差不是很大。

表3 不同固结压力下的试样孔隙率Table 3 Porosity for specimens underdifferent vertical loads

对4种不同颗粒棱角度的试样在不同竖向荷载（25、50、75 kPa）下进行剪切，得到的剪应力-剪应变曲线如图6所示。从图中可以看出，不同试样的剪应力-剪应变曲线均是先硬化后有稍许软化，这是由于每组试样在剪切前已经进行了充分的压缩固结，初始试样比较密实（见表 3）。在同一竖向荷载作用下带棱角的多面体颗粒试样的抗剪强度明显高于球形颗粒，并且试样抗剪强度随颗粒棱角度增大而增大。在竖向荷载较小的情况下，3种多面体颗粒试样的抗剪强度相差比较小，说明在较小竖向压力作用下颗粒的棱角度对抗剪强度的影响不是很大。

图6 不同竖向荷载条件下4种试样的剪应力-剪应变曲线Fig.6 Shear stress-strain curves of 4 specimens under different vertical loads

图7为4种不同颗粒试样的抗剪强度与竖向荷载关系曲线。剪应力τ=Aσ+c，其中A为内摩擦系数；c为黏聚力。计算结果：试样1，A=0.632，c=13.63 kPa；试样2，A=0.534，c=13.1 kPa；试样3，A=0.450，c=12.97 kPa；试样4，A=0.356，c=5.20 kPa。从图中可以看出，随着颗粒棱角度的增加，内摩擦系数A和黏聚力c均增加。带棱角的多面体颗粒试样的c要比球形颗粒试样大很多，说明颗粒棱角能够显著增加颗粒间的相互咬合作用。需要指出的是，在数值模型中的颗粒之间是没有粘接力的，这里的c更多地是反映颗粒间的相互咬合作用。

图7 峰值剪应力与竖向荷载关系曲线Fig.7 Relationships between peak shear strength and vertical load

4种不同颗粒棱角度的试样的体应变-剪应变曲线如图8所示。图中，体应变以正表示膨胀，负表示压缩。从图中可以看出，在剪切初始阶段4种试样的体应变保持为 0，原因是试样在剪切前已充分固结，水平方向的剪切扰动还不足以对试样内部结构造成影响。在相同竖向荷载作用下颗粒棱角度小的试样的剪胀性小；随着剪应变的增加，体应变先是快速增加，而后减缓并趋于临界状态。对于球形颗粒试样，体应变在较大竖向压力作用下表现为先体缩后体胀。同样经过充分固结的3种多面体颗粒试样，体应变一直表现为体胀。前后两者的不同可能是由于球形颗粒在剪切过程中能够自由转动，并且容易绕接触的颗粒翻转，从而沿水平方向的运动比竖向更容易。此外，增大竖向荷载相当于增加了颗粒的竖向约束，从而试样的剪胀性减小。

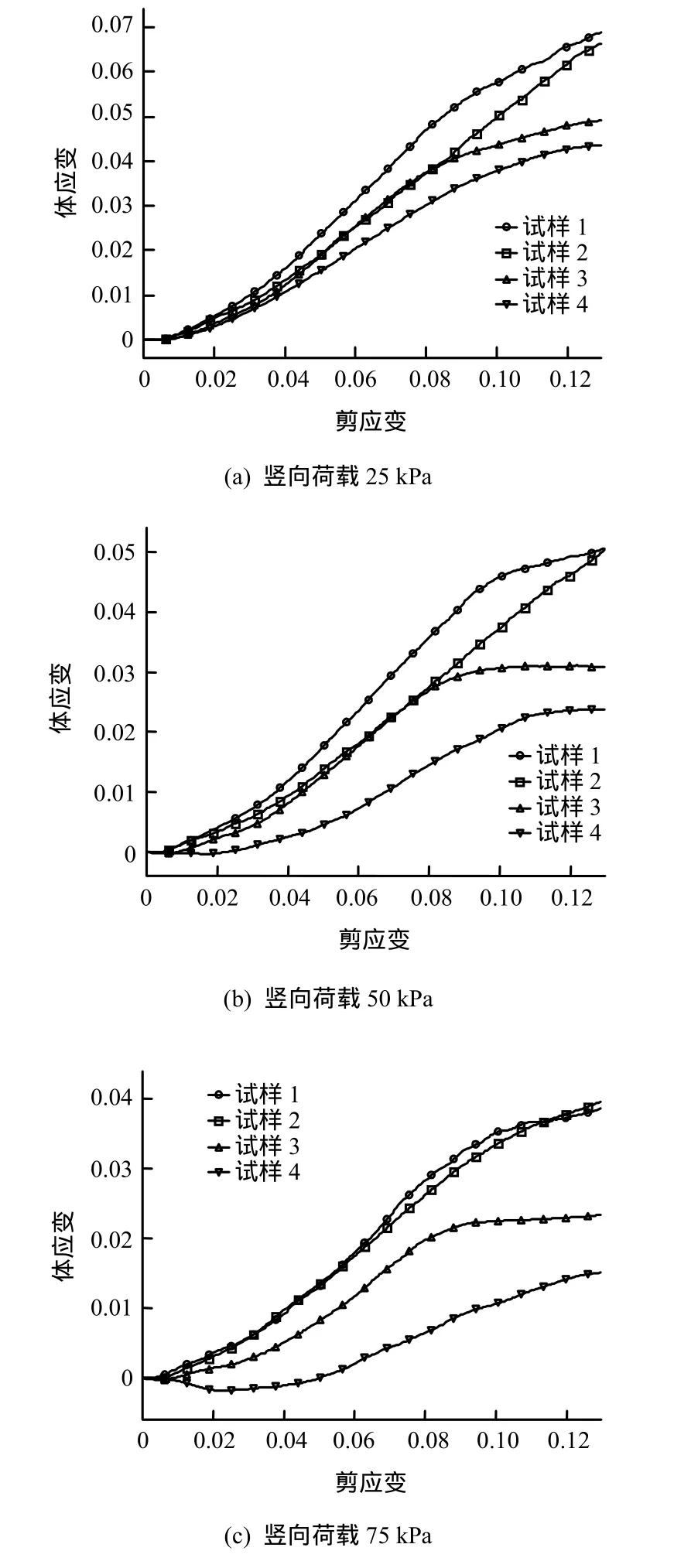
图8 不同竖向荷载条件下4种试样的体应变-剪应变曲线Fig.8 Volumetric strain-shear strain curves of 4 specimens under different vertical loads

4.2 接触力方向的各向异性

接触力方向的各向异性可用组构张量（fabric tensor）Φ表示，按式（8）计算：

式中：N为接触力总个数为第k个接触力的单位向量沿i（i=1，2，3为x、y、z方向）方向的分量。为了定量地描述接触力各向异性的演化规律，常用偏特征值[6，15]λd表示各向异性的大小程度：

式中：λ1、λ2、λ3为组构张量Φ的3个特征值。

4种不同颗粒棱角度试样在剪切过程中的法向接触力方向的各向异性演化规律如图9所示。剪切开始前，对于同一种颗粒棱角度试样，不同的固结压力下的法向接触力方向的各向异性不同，固结压力越大，法向接触力分布越不均匀，说明固结压力会对颗粒体系内部结构造成影响。在剪切过程中，竖向荷载越大，法向接触力方向的各向异性程度变化越小，说明较大的竖向荷载能够抑制法向接触力方向的各向异性的增加。同一竖向荷载下颗粒棱角度越大的试样，在剪切过程中表现出法向接触力方向的各向异性变化程度越大的趋势。

图9 不同竖向荷载下法向接触力的各向异性演化规律Fig.9 Evolution of anisotropy of normal contact force under different vertical load

法向接触力方向的各向异性演化曲线与剪应力-剪应变曲线有相似的变化规律，均表现为软化型曲线。剪切初期试样内部结构不断破坏，法向接触力方向的各向异性程度不断加大，达到一定水平的剪应变后试样内部颗粒重排基本结束，出现明显的剪切破坏带，颗粒运动主要表现为沿剪切面的移动，法向接触力方向的各向异性程度不断减小，随剪应变的发展而趋于稳定。

5 结 论

（1）颗粒棱角度越大，颗粒间的相互咬合自锁作用越强，颗粒在受剪过程中越难转动，致使颗粒体系的宏观抗剪强度和剪胀性增大。

（2）颗粒棱角度对颗粒体系的宏观抗剪强度和变形的影响程度与应力水平有关。在较高的外力水平所用下，颗粒棱角度的影响更明显。

（3）法向接触力方向的各向异性在剪切过程中表现为先增后减最后趋向稳定的趋势。颗粒棱角度越大，法向接触力方向的各向异性变化程度越大。

[1] CUNDALL P A, STRACK O D L. A discrete numerical model for granular assemblies[J]. Géotechnique, 1979,29(1): 47－65.

[2] INDRARATNA B, NGO N, RUJIKIATKAMJORN C,et al. Behavior of fresh and fouled railway ballast subjected to direct shear testing: Discrete element simulation[J]. International Journal of Geomechanics,2014, 14(1): 34－44.

[3] ZHOU B, HUANG R, WANG H, et al. DEM investigation of particle anti-rotation effects on the micromechanical response of granular materials[J].Granular Matter, 2013, 15(3): 315－326.

[4] KOZICKI J, TEJCHMAN J, MŰHLHAUS H B. Discrete simulations of a triaxial compression test for sand by DEM[J]. International Journal for Numerical and Analytical Methods in Geomechanics, 2014, 38(18):1923－1952.

[5] HOSSEININIA E S. Investigating the micromechanical evolutions within inherently anisotropic granular materials using discrete element method[J]. Granular Matter, 2012, 14(4): 483－503.

[6] ZHAO X, EVANS T M. Numerical analysis of critical state behaviors of granular soils under different loading conditions[J]. Granular Matter, 2011, 13(6): 751－64.

[7] 张翀, 舒赣平. 颗粒形状对颗粒流模拟双轴压缩试验的影响研究[J]. 岩土工程学报, 2009, 31(8): 1281－1286.ZHANG Chong, SHU Gan-ping. Effect of particle shape on biaxial tests simulated by particle flow code[J].Chinese Journal of Geotechnical Engineering, 2009,31(8): 1281－1286.

[8] 孔亮, 彭仁. 颗粒形状对类砂土力学性质影响的颗粒流模拟[J]. 岩石力学与工程学报, 2011, 30(10): 2112－2119.KONG Liang, PENG Ren. Particle flow simulation of influence of particle shape on mechanical properties of quasi-sands[J]. Chinese Journal of Rock Mechanics and Engineering, 2011, 30(10): 2112－2119.

[9] TING J M, MEACHUM L, ROWELL J D. Effect of particle shape on the strength and deformation mechanisms of ellipse-shaped granular assemblages[J].Engineering Computations, 1995, 12(2): 99－108.

[10] NG T T. Particle shape effect on macro- and micro-behaviors of monodisperse ellipsoids[J].International Journal for Numerical and Analytical Methods in Geomechanics, 2009, 33(4): 511－527.

[11] ŠMILAUER V, CATALANO E, CHAREYRE B,et al. Yade documentation(the 1st version)[EB/OL].http://yade-dem.org/doc/, 2010. 2013-10-22.

[12] NASSAUER B, LIEDKE T, KUNA M. Polyhedral particles for the discrete element method[J]. Granular Matter, 2013, 15(1): 85－93.

[13] ELIÁŠ J. Simulation of railway ballast using crushable polyhedral particles[J]. Powder Technology, 2014, 264:458－465.

[14] GÜNTHER O, WONG E. A dual approach to detect polyhedral intersections in arbitrary dimensions[J]. BIT Numerical Mathematics, 1991, 31(1): 2－14.

[15] BARRETO D, O'SULLIVAN C, ZDRAVKOVIC L.Quantifying the evolution of soil fabric under different stress paths[C]//Proceedings of the 6th International Conference on Micromechanics of Granular Media.London, UK: [s. n.], 2009, 1145: 181－184.