考虑卸荷效应钻孔灌注桩孔径时空变化规律研究
赵春风 ,陈洪祥 ,赵 程 ,薛金贤
(1. 同济大学 岩土及地下工程教育部重点实验室,上海 200092;2. 同济大学 地下建筑与工程系,上海 200092;3. 深圳高速工程顾问有限公司,广东 深圳 518000)
1 引 言
钻孔灌注桩在桩位处成孔时使孔壁的侧压力得到解除,形成较大的自由面,使地层压力向自由面应力释放,在远场地应力作用下造成孔壁土体向内收缩,出现“缩孔现象”,产生卸荷效应,不可避免地对原有土体产生了扰动,造成土体的应力场和位移场发生变化,削弱了桩周土的应力,使应力不平衡而失稳[1-2]。
钻孔后孔体随时间的卸荷效应不容忽视,受到土质、施工工艺、钻机类型、泥浆指标等因素的影响。各种外界因素对孔壁扰动的累积效应可以通过孔径的变化反映出来,孔径的变化揭示出这些影响因素随时间累计的作用效果。因此,衡量成孔质量的有效手段就是分析桩孔穿越土层后孔径的变化值,得到孔径随时间及空间的变化特征[3]。
2 工程地质概况
本工程数据来自上海浦东地区某高层住宅小区钻孔灌注桩施工过程中的的原始施工记录、工程地质勘察报告和试成孔质量检测资料。土层物理力学指标见表1。
3 不同土层孔径随时间的变化
本工程的试成孔孔径测量在钻孔结束后24 h内进行,共测量4次孔径,第一次测量在钻孔结束后立即进行,以后3次测量的时间间隔分别为6、6、12 h。通过对少数钻孔孔径的连续测量,可统计不同钻孔孔径随钻孔时间的变化,减小了不同钻孔的差异所造成的影响,能够更真实地反映出孔径随时间的变化规律。
根据本工程情况,选取 0#、1#、3#、6#楼各 2个试成孔和5#楼的一个试成孔,共计9个试成孔数据。从统计结果来看,在孔深8.6 m以上土层范围内,孔径随时间变化比较大,但没有较为一致的变化方向,非严重塌孔即明显缩颈。究其原因,从地质勘察报告来看,这个范围内的土层为淤泥质粉质黏土,土层稳定性较差,且浅部土层受施工和地面的扰动较深层土更严重,因此这个范围内的孔壁变化极不规律,故统计时剔除这个深度范围内的数据,只保留余下相对稳定的数据。
不同土层的孔径变化曲线如图1所示。从图中可以看出,所有土层的孔径都发生了缩小,且随着时间的推移,缩小量逐渐增加,可知孔径缩小量与时间具有正相关的关系。仔细分析图表可以得知,在 0~12 h内,第④、⑤-1a、⑤-1b、⑥、⑦1、⑦2土层的累计变化量分别为6.2、5.0、6.0、4.9、6.8、8.8 mm,已经占到24 h总变化量的69%、62%、68%、78%、65%、70%,所以,不同土层平均孔径的缩小值随时间的增长不是线性增加的,而是前期增加量大,而后逐渐减小,最后趋于稳定。
钻孔灌注桩成孔完成后,不同土层在相同的时间内所对应的孔径缩小值是不一样的,在埋深24.6 m以上,即从第④~⑥层,随着土层的埋身越大,其缩小量越小;埋深24.6 m以下,随着土层的埋深增加,其缩小量反而增加,且该处土层不太稳定,其缩小量远远超过24.6 m以上的土层。分析原因,可能与各个土层的物理力学性质存在差异有关,观察地质勘察报告可以发现,⑦1层砂质粉土层和⑦2层粉砂层力学强度指标较小,土层的稳定性较差。

图1 不同土层内平均孔径缩小值与时间关系曲线Fig.1 Relationships between average bore diameter reduction and time in different soil layers
为分析不同土层内孔径随时间的变化规律,采用归一法对数据进行分析处理,运用最小二乘法对所测数据进行拟合,公式为
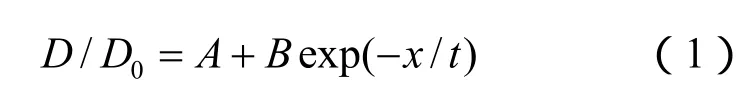
式中:D为不同时间土层平均孔径值;D0为土层初始孔径值;x为时间;A、B、t为待定参数。
具体参数见表 2。根据现场实测数据和拟合公式绘制不同土层的平均孔径值/初始孔径值与时间的关系曲线如图2所示。从图中可以看出,各土层的拟合曲线逐渐趋于平缓,说明孔径的变化随时间增长趋于稳定,⑦1层淤泥质黏土层的孔径变化是最大的,也是最不稳定的,⑦2层粉砂层的孔径变化次之,较不稳定,⑥层粉质黏土层的孔径变化最小,④、⑤1a层和⑤1b层的变化较为一致。拟合公式的拟合度较高,同时拟合曲线能够真实地反映出不同土层的孔径随时间的变化特征。
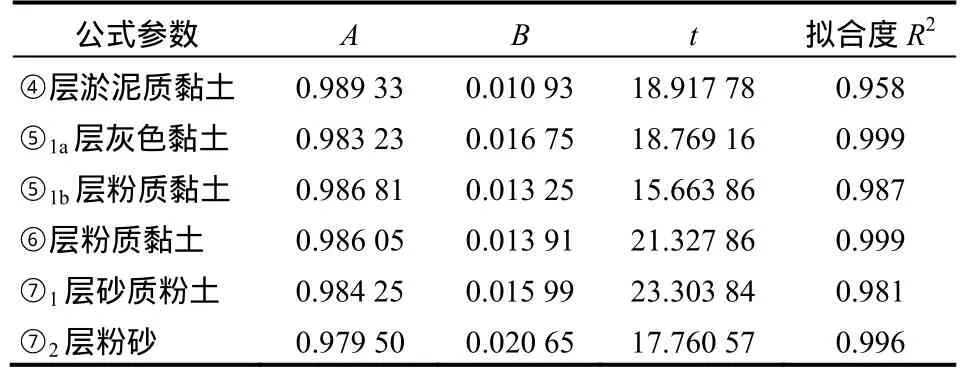
表2 不同土层孔径变化公式Table 2 Change formulas of hole diameter in different soil layers

图2 不同土层内平均孔径值/初始孔径值与时间关系Fig.2 Relationships between ratio of average bore diameter and initial bore diameter and time in different soil layers
4 钻孔特性的力学分析
4.1 基本假设和力学模型
成孔后的土体由若干层高度有限平面无限的弹性体组成,只受自重应力σz的作用,圆柱形桩孔的深度远大于孔径,孔壁仅受到泥浆的压力q(以压为正)作用,泥浆对孔壁的冲刷作用和机械对孔壁的影响忽略不计,各土层交界面为平面,以地面桩孔中心处建立柱面坐标系,Z轴竖直向下[4]。计算公式为

式中:γs为泥浆相对重度;γi为第i层土重度,水面以下取有效重度;h为泥浆液面高出地面的高度。
沿Z轴取出任何一个平面进行受力分析,可按照平面应变问题进行计算,弹性力学的解答为
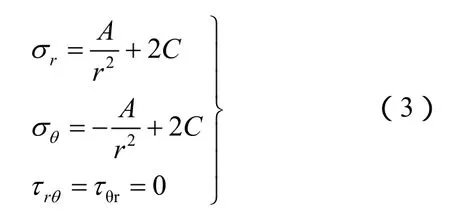

式中:ur为孔壁的位移;ν为土的泊松比;E为弹性模量。

式中:r0为桩孔半径;K0为静止土压力系数。
4.2 孔径变化公式推导
根据平均孔径的变化绘制了孔径缩小值和时间的关系曲线见图 1。孔径的缩小值是逐渐增大并趋于稳定的,这是由于真实的土体的变形包含了土的弹性、塑性和黏性的特点。考虑到黏弹性模型中的Kelvin模型[5]能够描述岩土的黏弹性,即在应力作用下应变不是立即达到弹性应变的最终值,而是有一个相对滞后的现象。本构方程为

其曲线形式和孔径缩小值和时间的关系曲线一致,随着时间增长其应变逐渐趋于稳定值,这与章节4.1中对平均孔径随时间变化拟和的公式具有相似性:随时间增长D/D0趋于定值A,因此可以认为(1-A)r0即为最终总的弹性变形,即


将通过弹性理论计算得到的ur/r0值代入拟合所得公式中,可得到更为理想且可以反映土体黏弹性的孔径变化规律。
4.3 钻孔稳定性分析
文献[6]提到可用应力坡角θ描述孔壁的稳定性:

当r=r0时,sinθ最大,即在孔壁处最不稳定,随者r值的增大sinθ迅速减小,孔壁外土体的稳定性很快得到提高,该公式表明,黏聚力c越大,内摩擦角φ越小,孔壁稳定性越好,从而可解释在前文从④层淤泥质黏土到⑤层灰色黏土再到⑥粉质黏土层的钻孔平均孔径波动逐渐减小,平均孔径维持稳定时间逐渐增长的内在机理。对于⑦1层砂质粉土和⑦2层粉砂的c值很小,个别单体的c值接近于0,也最不稳定,表现为孔径的减小最为明显,孔径波动的幅度也较大。
5 结 论
(1)上海地区孔深8.6 m以上多为淤泥质黏土,这个范围内得到的孔径实测数据离散型较大,且埋藏较浅,受外界干扰的因素太多,孔径变化极其不规律,故在对数据进行整理分析时应将其剔除,有利于排出干扰,得出正确结论。
(2)孔径的缩小量与时间呈正相关,缩小幅度逐渐减小,最后趋于稳定。采用最小二乘法,将所测得的孔径变化数据用式(1)进行拟合,拟合度较高,能够反映孔径变化的特点和规律。
(3)空间上,相同时间内、不同物理力学性质的土层孔径变化量也不同,黏聚力c越小,内摩擦角φ越大,稳定性就越差,表现为该土层的孔径变化量越大,其中④层淤泥质黏土层及⑦1层砂质粉土层易发生塌孔,⑦1层砂质粉土层及⑦2层粉砂层易发生缩颈。
(4)基于Kelvin模型,运用弹性理论,结合拟和公式,推导出更符合实际的孔径变化公式和反映出孔壁稳定性的公式,并合理地解释了不同土层稳定性差异的原因。
[1] 赵春风, 王学知, 赵洪平, 等. 考虑混凝土性质变化灌注桩深部土压力分析[J]. 同济大学学报(自然科学版),2009, 37(7): 878-882.ZHAO Chun-feng, WANG Xue-zhi, ZHAO Hong-ping,et al. Analysis of deep earth pressure around cast-in-place pile considering concrete property variation[J]. Journal of Tongji University(Natural Science), 2009, 37(7): 878-882.
[2] 杨砚宗. 砂土考虑卸荷效应的钻孔灌注桩试验与理论研究[D]. 上海:同济大学, 2011.
[3] 龚辉. 黏性土中钻孔灌注桩径向卸荷效应及其对桩侧摩阻力的影响机制[D]. 上海:同济大学, 2013.
[4] 吴家龙. 弹性力学(第2版)[M]. 上海:同济大学出版社, 1997.
[5] 殷宗泽. 土工原理[M]. 北京:中国水利水电出版社,2007.
[6] 蒋红心, 胡中雄. 钻孔孔壁的稳定性分析[J]. 工程勘察,1999, 24(3): 7-10.JIANG Hong-xin, HU Zhong-xiong. Analysis on stability of borehole wall[J]. Geotechnical Investigation &Surveying, 1999, 24(3): 7-10.

