水位波动下非饱和心墙土坝体的渗流和稳定性
陈 曦,张训维,陈佳林,金 锋,于玉贞
(1.北京交通大学 土木建筑工程学院,北京 100044;2. 清华大学 水沙科学与水利水电工程国家重点实验室,北京 100084)
1 引 言
我国水库大坝建设历史悠久,全国已建成大小水库总数量接近9万座。 部分水库的坝体由于长期服役,存在不同程度的隐患,环境的变化是诱发水库风险的主要因素,例如,降雨入渗、水库蓄水后库水位骤降都可能引起水库坝体安全系数下降,导致坝体危险产生。 许多学者对库水位波动所引起的坝体渗流和坝体稳定性变化进行了研究。 刘新喜等[1]基于 Richards饱和-非饱和渗流控制方程建立了有限元格式,分析了库水位骤降时的瞬态渗流场,评价了渗流力作用下滑坡稳定性分析的不平衡推力法,并认为滑坡的渗透系数和库水位下降速度是影响坝体稳定性的主要因素。张文杰等[2]基于GeoStudio中的Seep/W和Slope/W模块对库岸边坡的渗流场和稳定性进行了分析,其非饱和土的抗剪强度基于 Fredlund公式,稳定性分析基于 Bishop极限平衡法,最后给出了坡体安全系数随水位波动的变化曲线。陈曦等[3]认为非饱和土坡稳定性分析方法的发展可分为3个阶段,即时间无关的定性分析阶段、时间相关的渗流和变形不完全耦合分析阶段以及时间相关的渗流和变形完全耦合的分析阶段,目前渗流稳定性分析方法以第二或第三阶段的分析方法为主。徐炎兵等[4]则基于多孔介质理论,建立了非饱和土两相流动与变形的耦合模型,开发了有限元分析程序,并采用经典算例和离心机试验对数值结果进行了验证。
本文采用渗流与变形的不完全耦合分析方法,即先采用Richards方程进行非饱和渗流场的有限元求解,再基于非饱和渗流场和非饱和土的抗剪强度理论对坝体的稳定性进行评价,通过数值算例分析了水库库水位波动对坝体稳定性的影响。
2 非饱和土渗流Richards方程
2.1 非饱和土土-水特征曲线模型
常用的土-水特征曲线模型有Brooks-Corey 模型,Van Genuchten模型(简称VG模型)和Fredlund-Xing 模型。由于VG模型具有连续平滑的曲线,在进气压力值和接近残余含水率状态时具有较好的平滑过渡,本文采用VG土-水特征曲线模型,表达式为

式中:h为压力水头;θ、θr、θs分别为当前体积含水率、残余体积含水率和饱和体积含水率;av、nv、mv为经验系数,mv通常简化为mv=1- 1 /nv。VG模型通常是av、nv、mv的3参数的模型,当θs、θr不能直接给出时,VG模型可作为 5参数模型。式(1)也可表示为标准化的体积含水率Θ,即

非饱和渗流的水力传导系数可采用Mualem公式进行描述:

式中:经验参数l一般取为1.0;ks为饱和水力传导系数,为常数;kr(Θ)为相对渗透张量,是有效饱和度Θ的函数。
2.2 非饱和渗流有限元求解
非饱和土渗流建模的Richards方程可采用3种基本格式,即压力水头格式(h-form)、体积含水率格式(θ-form)和混合格式(mixed form),下面的压力水头格式的Richards方程应用更为广泛,

式中:s为源汇项;η为比存储量或土-水特征曲线的导数,即

式中:γw为水的重度;mw为土-水特征曲线的斜率。
对式(4)进行空间离散和时间差分,可得Richards有限元方程的修正Picard迭代公式:

式中:下标n、m分别为时间步指标和修正Picard方法迭代步指标;M、C分别为质量矩阵和水力传导特征矩阵。
3 非饱和土抗剪强度与稳定性分析
进行非饱和土体的稳定性评价时需要采用合理的非饱和土抗剪强度理论,Sheng等[5]认为,尽管目前所提出的非饱和土抗剪强度理论和公式较多,但大多可以看作是 Bishop和 Blight强度理论和Fredlund强度理论的变体,各种非饱和土强度理论的主要差别在于参数或变量的选取不同。Bishop和Blight强度理论一般可表示为
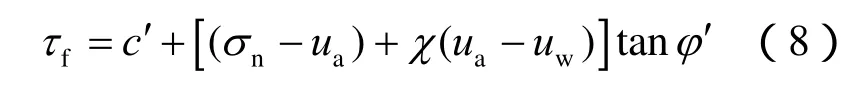
式中:c′、φ′分别为土的有效黏聚力和有效内摩擦角;χ为与饱和度(Sr)相关的参数;Fredlund强度理论考虑了一个描述基质吸力对剪切强度贡献的角度φb,则式(8)可表示为

式中:抗剪强度公式中第三项是基质吸力的贡献,可将其合并到真黏聚力,形成“假黏聚力”c′,即

对于 ta nφb,本文采用 Fredlund-Oberg公式,即

土体稳定性分析方法较多,其中有限元强度折减法实际应用效果良好[6]。为了获得应力和应变分布、位移场,塑性分布等更多信息,本文采用有限元强度折减法进行土体稳定性分析,仍为基于单网格强度折减技术,为获得更高的求解效率,可以采用双网格强度折减技术[7]。
4 水位波动条件下坝体渗流和稳定性分析
4.1 坝体临水坡坡度大于背水坡坡度的算例
USSA为开发的非饱和土渗流与稳定性分析软件,用户界面采用Python脚本语言,主计算程序采用FORTRAN语言,并通过算例验证了计算程序的可靠性[8]。如图1所示,算例1为均质土坝,其左右坡坡度分别为1︰1.8和1︰1.4;土坝左侧初始水位为0 m,右侧初始水位为7.05 m。在此初始条件下达稳态渗流后,右侧水位从初始水位以1 m/d的较快速度下降,最后水位降为0 m。图2为水位下降过程中坝体边坡安全系数的变化过程,实线和实心标识为真正的边坡安全系数。在水位下降不超过4.11 m时,左侧边坡为危险边坡,并先于右侧边坡发生破坏;当水位下降超过4.11 m时,右侧边坡先于左侧边坡发生破坏。虚线和空心标识为猜测的左右侧边坡安全系数演化过程,即随着水位下降,左侧边坡的安全系数缓慢增加,右侧边坡的安全系数由于水压的降落而迅速减少,并在水位下降超过4.11 m时,开始小于左侧边坡的安全系数。水位下降过程中,左侧边坡安全系数缓慢增加归因于非饱和区比例的逐渐增加;右侧边坡则相对复杂,由于水压降落的影响要高于非饱和区比例逐渐增加的影响,导致右侧边坡安全系数的总体变化趋势是减小的。左右侧坡体安全系数变化曲线相交点约为FOS≈1.56。

图1 均质土坝有限元网格划分Fig.1 Finite element mesh of homogeneous soil dam
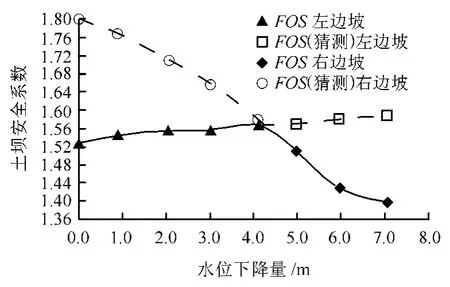
图2 水位降低过程中均质土坝安全系数的变化曲线Fig.2 Variation curves of safely factor with the drawdown of water level for homogeneous dam
4.2 坝体临水坡坡度等于背水坡坡度的算例
算例2的整个区域由3种土组成,即坝体土体、坝体心墙材料和坝基土体,如图3所示为整体分析区域的有限元网格划分。3种土体的弹塑性力学参数见表 1,其中φ、φ分别为土的内摩擦角和剪胀角。非饱和土土性参数见表2。3种土的不饱和自然重度和饱和重度分别为17 kN/m3和20 kN/m3,其中坝基和心墙材料采用非饱和土数据库 UNSODA中编号为3 091的砂质壤土和编号为1 183的黏土[9]。

图3 土坝有限元网格划分Fig.3 Finite element mesh of earth dam with core wall

表1 坝体土体弹性和强度力学参数Table 1 Elastic and strength parameters for dam soils
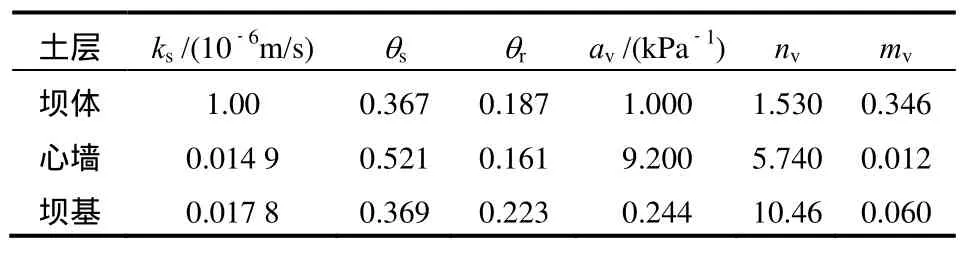
表2 坝体土体非饱和土性参数Table 2 Unsaturated hydraulic parameters for soils of dam
首先模拟没有心墙的情况,坝体在右侧水位为38 m,左侧水位为0 m条件下达稳定渗流。分别采用0.01 m/d和 1 m/d两种不同的水位下降速度,分析了水位下降过程中坝体安全系数的变化,如图 4所示。对于无心墙坝体,当水位下降速度较低时(如0.01 m/d),坝体的安全系数呈缓慢稳定增长趋势;但是当水位下降速度较快(1 m/d时),安全系数基本维持在某一值(2.27~2.28)附近,直到水位下降了34 m或下降到4 m左右,安全系数开始明显减小。可由图5来理解上述变化,对于左侧坡体,水位下降到26 m时和水位下降到0 m时的自由液面相差较小,而在右侧坡体内则相差较大。当右侧坡体缺少足够的水压力保护时,右侧坡体的安全系数开始小于左侧坡体,这与算例1的情况类似,只不过由于左右侧坡体坡度不同,左右侧坡体安全系数变化曲线的相交点的位置也有所不同。

图4 不同水位下降速度时无心墙坝体安全系数变化曲线Fig.4 Variation curves of safely factor for different drawdown speed of water level for dam without core wall

图5 水位以1 m/d速度下降到26 m和0 m位置时的自由液面Fig.5 Phreatic surface when water level reaches 26 m and 0 m, respectively
考虑心墙时,心墙与坝体材料见表1、2。坝体在右侧水位为38 m,左侧水位为0 m条件下达稳定渗流,此时坝体、心墙和坝基的体积含水率的分布阴影图和压力水头分布如图6所示。从图中可以看出,自由液面以下土体都达到各自的饱和体积含水率,心墙的饱和体积含水率(0.521)明显高于坝体和坝基土体的饱和体积含水率。
同样,坝体右侧水位从38 m分别以0.01 m/d和1 m/d的速度下降。图7为水位下降过程中安全系数的变化曲线。从图中可以看出,由于心墙的存在,坝体安全系数略高于无心墙的情况。对于不同的水位下降速度,在水位下降了34 m或下降到4 m左右,安全系数都有明显的减小,且在水位下降为0 m时都有回升。图8为以0.01 m/d的水位下降速度,水位分别下降至26 m和0 m时坝体内体积含水率阴影图。由于渗透性较低,心墙会对左侧坡体的自由液面下降起到一定的阻尼作用。

图6 水位38 m时的稳态渗流场Fig.6 Finite element mesh of earth dam with core wall

图7 不同水位下降速度时心墙坝体安全系数变化曲线Fig.7 Safely factor curves of dam with core wall for different drawdown speed of water level

图8 水位下降速度为0.01 m/d时坝体内体积含水率阴影Fig.8 Contour of volumetric water content in dam for water level drawdown speed of 0.01 m/d
以左右两侧为0 m水位条件下达稳定渗流,在此条件下分别以 0.01 m/d和1 m/d的速度蓄水。图 9为水位上升过程中安全系数的变化曲线。可见,在水位上升初期,即约为0~8 m时,安全系数会有所提高,表明这个期间由于水压的施加,右侧边坡的安全度一直增加,而左侧边坡的安全度随着渗流的发生,非饱和区逐渐减小,自重增加,导致其安全系数逐渐减小。在达到约8 m水位后,安全系数开始小于右侧边坡。因此,水位上升过程中安全系数变化曲线亦可看成左右侧坡体安全系数交叉获得的曲线。需要说明的是,水位上升速度较快(即1 m/d)时,由于心强的隔水和防渗作用,左侧坡体渗流自由液面较低,安全系数下降较为平缓,而水位上升速度较慢(即0.01 m/d)时,安全系数下降更为明显。

图9 不同水位上升速度时心墙坝体安全系数演化曲线Fig.9 FOS curves for different rise speed of water level
5 结 论
(1)左右坝体边坡各存在一条安全系数变化曲线,真实的安全系数变化曲线是这两条安全系数变化曲线交叉获得的较小的部分。
(2)水压对坝体边坡的稳定性具有重要的影响,通常高水位有益于临水边坡的稳定性,而临水边坡的稳定性通常由水压和非饱和区比例变化共同支配。
(3)背水面边坡的分析相对简单,在水位变化过程中背水面边坡的非饱和区的比例变化所支配。
(4)心墙具有对水位变化所产生的背水面坡体渗流场变化的阻尼作用。
[1] 刘新喜, 夏元友, 练操, 等. 库水位骤降时的滑坡稳定性评价方法研究[J]. 岩土力学, 2005, 26(9): 1427-1431.LIU Xin-xi, XIA Yuan-you, LIAN Cao, et al. Research on method of landslide stability valuation during sudden drawdown of reservoir level[J]. Rock and Soil Mechanics, 2005, 26(9): 1427-1431.
[2] 张文杰, 陈云敏, 凌道盛. 库岸边坡渗流及稳定性分析.水利学报, 2005, 36(12): 1510-1516.ZHANG Wen-jie, CHEN Yun-min, LING Dao-sheng.Seepage and stability analysis of bank slopes[J]. Journal of Hydraulic Engineering, 2005, 36(12): 1510-1516.
[3] 陈曦, 刘春杰. 逐步完善的非饱和土边坡稳定性有限元分析方法[J]. 岩土工程学报, 2011, 33(增刊1): 380-384.CHEN Xi, LIU Chun-jie. Staged development of finite element methods for stability of unsaturated soil slopes[J].Chinese Journal of Geotechnical Engineering, 2011,33(Supp.1): 380-384.
[4] 徐炎兵, 韦昌富, 李幻, 等. 非饱和土渗流与变形耦合问题的有限元分析[J]. 岩土力学, 2009, 30(5): 1490-1496.XU Yan-bing, WEI Chang-fu, LI Huan, et al. Finite element analysis of coupling seepage and deformation in unsaturated soils[J]. Rock and Soil Mechanics, 2009,30(5): 1490-1496.
[5] SHENG D, ZHOU A N, FREDLUND D G. Shear strength criteria for unsaturated soils[J]. Geotechnical and Geological Engineering, 2011, 29(2): 145-159.
[6] 于玉贞, 林鸿州, 李荣建, 等. 非稳定渗流条件下非饱和土边坡稳定分析[J]. 岩土力学, 2008, 29(11): 2892-2898.YU Yu-zhen, LIN Hung-chou, LI Rong-jian, et al.Stability analysis of unsaturated soil slope under transient seepage flow state[J]. Rock and Soil Mechanics, 2008,29(11): 2892-2898.
[7] CHEN X, WU Y, YU Y, et al. A two-grid search scheme for large-scale 3-D finite element analyses of slope stability[J]. Computers and Geotechnics, 2014, 62: 203-215.
[8] 陈曦, 于玉贞, 程勇刚. 非饱和渗流 Richards 方程数值求解的欠松弛方法[J]. 岩土力学, 2012, 33(增刊 1):237-243.CHEN Xi, YU Yu-zhen, CHENG Yong-gang. Underrelaxation methods for numerical solution of Richards equation of variably saturated flow[J]. Rock and Soil Mechanics, 2012, 33(Supp.1): 237-243.
[9] NEMES A, SCHAAP M G, LEIJ F J. The UNSODA unsaturated soil hydraulic database(version 2.0)[M].Riverside, CA: US Salinity Laboratory, 1999.

