利用Mathematica软件提高经济数学的教学效果

陆卫丰

(苏州市职业大学 数理部，江苏 苏州 215104)

利用Mathematica软件提高经济数学的教学效果

陆卫丰

(苏州市职业大学 数理部，江苏 苏州 215104)

利用Mathematica软件和多媒体工具，解决经济数学教学过程中出现的理论与计算方面存在的一些问题，从而激发学生学习经济数学的兴趣，使教学效果得到显著提高.

经济数学；Mathematica 软件；教学效果

经济数学[1-3]作为大学经济管理类专业的基础课程，包含了微积分、概率统计、线性代数等知识内容，对后续经济学课程的重要性是显而易见的[4-5].作为大学数学课程，其特点是理论性比较强，实践环节比较少，教学方式相对传统，学生学习的兴趣不高，学习难度也就比较大，这一特点在高职高专类学校尤为明显.能让学生从深奥的理论与繁重的计算中解脱出来，激发学生的学习兴趣，是学好经济数学课程的关键.如今很多学校的教室都配备了计算机和多媒体工具，合理利用这些教学工具可以提高课堂教学效果，同时也是对传统课堂教学的创新尝试与改革.

Mathematica软件具有强大的数值计算与符号计算能力，函数绘图功能也很强大，操作界面简单并且直观[6].将它与经济数学课程相结合，利用多媒体工具作为演示窗口，可以改善教学效果，使课堂教学不再枯燥死板，学生学习兴趣可以得到激发，从而提高学生学习经济数学的积极性与主动性.本文将从三个方面分析利用Mathematica软件来提高经济数学教学效果.

1 数形结合，帮助学生理解抽象问题

经济数学课程中有相当一部分内容是基础的理论知识，例如概念、定理、公式等，学生对这些内容的理解程度将直接影响其学习经济数学的效果.然而这些理论知识往往是比较抽象的，学生感到头疼.Mathematica软件的计算与绘图能力将有助于教师将这些枯燥的内容形象化、具体化、生动化.

例如，在极限学习的过程中，“两个重要极限”是非常重要的概念，其中第二个重要极限的数列形式与经济学的关系也比较密切.在具体的教学过程中可以利用经济学实际案例将它引出，然后就演变成了如下问题[1].

例1 给定数列，观察数列的变化趋势，讨论数列的极限.

教材中有一张表格记载着n逐渐变大时数列的变化趋势，然而学生对于课本上的内容印象不是太深刻，此时可以引入Mathematica软件在课堂上作演示.

定义函数，输入命令：f[n_]：=(1+1/n)^n

输入具体的值作对比，例如f[1.]，f[2.]，…，f[100.]

也可以使用列表命令：N[Table[f[n]，{n，1，100，1}]]，运行后屏幕上会出现当n从1到100时数列的值{2，2.25，2.370 37，2.441 41，…，2.704 68，2.704 81}.学生可以看到数列的变化趋势.

为了进一步得到比较简单的极限结果，可以采用极限命令：N[Limit[f[n]，n-＞1000]]，得到结果2.716 92，然后将命令里的1 000改为10 000，100 000，200 000等，依次得到结果2.718 15，2.718 27，2.718 28，可以让学生更清楚地看到数列的变化趋势.

当输入Limit[f[n]，n-＞Infinity]时，得到结果e，然后就可以让学生知道当n趋于无穷大时这个数列的极限记做e，即，同时也记住了e≈2.718 28.

为了给学生一个更直观、更形象的数列极限变化的过程，可以采用如下图形命令演示：

tu1=ListPlot[Table[f[n]，{n，1，30}]，PlotRange-＞{2，E}，PlotStyle-＞PointSize[0.01]]；

tu2=Plot[E，{x，1，100}，PlotStyle-＞RGBColor[1，0，0]]；

Show[tu1，tu2]

得到如图1显示的结果，随着n增大，图中散点逐渐接近直线y=e.通过观察图形中散点的变动，学生可以进一步了解数列的具体变化趋势，随着n越来越大，数列的值的变动越来越稳定，并且越来越靠近数值e.这就是教材中数列极限的定义：给定一个数列{xn}，如果当n无限增大时，xn无限接近于一个确定的常数A，则称当n趋于无穷时，数列{xn}的极限为A.通过图形演示，学生对数列极限的抽象定义有了一个较为具体形象的了解，便于深刻掌握.

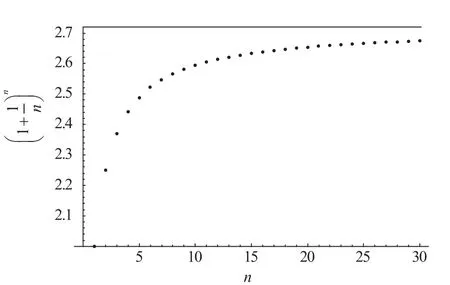
图1 第二个重要极限散点图

2 强大的数值计算能力，辅助教学过程

经济数学课程中有一些问题的解决是需要学生在课堂上通过比较繁复的计算来完成的，例如概率统计、线性代数中的一些问题.但是由于教学时间有限制，在课堂上并不能够给学生提供充足的计算时间；有时候即使提供了一些时间给学生计算，还是有相当一部分学生由于计算能力不强、偷懒等原因不去计算.对于这种情形，教师只能将计算的原理、过程、步骤、结果一一讲述或者写到黑板上，教学形式呆板.这样不但浪费大量的教学时间，而且由于学生缺乏学习兴趣，教学效果也将大打折扣.Mathematica软件具有强大的数值计算能力，可以完成在解决问题中出现的复杂计算，同时学生会被软件所吸引，学习兴趣也会被唤起.

例如,在二项分布和泊松分布中有一个问题[2].

例2 一本书有200页(每页的印刷符号超过500个)，全书一共出现了500个印刷错误，假设每个错误是等可能的出现在各页的，问第一页出现6个以上错误的概率.

在求解过程中，设随机变量X是第一页出现错误的数量，则X服从二项分布B(500，1/200)，第一页出现6个以上错误的概率为

这时如果让学生用计算器计算上面这个式子，比较繁琐，将花费很多课堂时间，一些学生计算会出错，或者有些学生干脆不去计算；而如果教师直接告诉答案，学生会对答案的正确性提出疑问，同时印象并不深刻.这时可以利用Mathematica软件在课堂上演示.1-Sum[500!/(k!*(500-k)!)*(1/200)^k*(199/ 200)^(500-k)，{k，0，5}]，或者直接计算Sum[500!/(k!*(500-k)!)*(1/200)^k*(199/200)^(500-k)，{k，6，500}]》.会得到答案：0.041 602 8，即第一页出现6个以上错误的概率约为0.042，这样让学生信服的同时也提高了他们的学习兴趣.

接着在Mathematica软件中取λ=500×(1/200)=2.5，用泊松分布来计算概率

教学时教师可以先不介绍泊松分布表，直接利用Mathematica软件在课堂上做演示.

λ=500/200；1-Sum[λ^k/k!*E^(-λ)，{k，0，5}]，会得到答案：0.042 021，约为0.042，与用二项分布计算的“第一页出现6个以上错误”的概率约为0.042基本相同.此时再顺理成章引入泊松定理，便于学生记忆与理解.

3 为问题的多种解决方法提供实践条件

经济数学课程中有时同一个问题会有多种解决方法，例如线性代数中的一些问题.而各种方法之间存在联系与区别，每一种方法具有优点与缺点，使用哪一种方法更为简单合理.回答这些问题的最好办法就是将多种方法都演示给学生，但是由于教学时间有限制，传统教学中通常并不能做到这一点.Mathematica软件具有强大的数值计算与符号计算能力，它的使用将节约大量的计算时间，从而教师可以演示更多的方法，让学生更好地分析问题、理解问题和解决问题.

例如，在介绍完矩阵初等变换以后，给出一个解n元线性方程组问题[2]

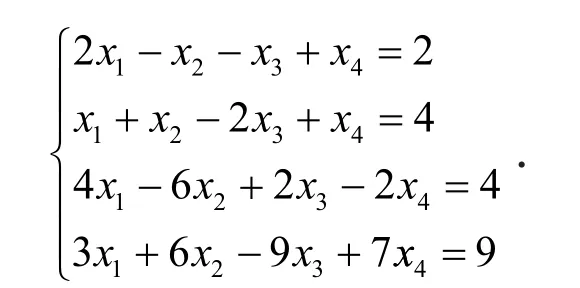
教师可以给学生提供一些方法求解：克莱姆法则法、逆矩阵法、高斯消元法、矩阵初等变换法.传统教学方式中每一种方法的演示都需要比较多的时间，此时选择利用Mathematica软件在课堂上演示.

1) 克莱姆法则法.需要先求系数行列式，定义方程组的增广矩阵AB.

取出系数矩阵A和常数列向量B：A=Table[A[[i，j]]，{i，1，4}，{j，1，4}]；B= Table[A[[i，5]]，{i，1，4}].求系数矩阵A的行列式.Det[A]得到结果为0，说明该方程组不能使用克莱姆法则求解.

2) 逆矩阵法.用系数矩阵A的逆矩阵A-1乘以常数列向量B：Inverse[A].B提示结果：Matrix is singular.说明矩阵A不可逆，所以该方程组不能使用逆矩阵法求解.同时验证了方阵的行列式为0与方阵不可逆的等价关系.

3) 高斯消元法.直接求解方程Solve[{2x1-x2-x3+x4□2，x1+x2-2x3+x4□4，4x1-6x2+2x3-2x4□4，3x1+6x2-9x3+7x4□9}，{x1，x2，x3，x4}]

得到结果：{{x1→4+x3，x2→3+x3，x4→-3}}，即得到解

4) 矩阵初等变换法.利用矩阵的初等行变换将方程组的增广矩阵AB化为行最简矩阵：

得到结果

即得到解

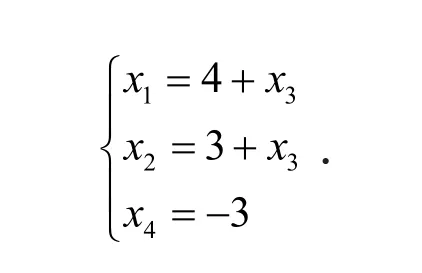
学生可以对比这几种方法.

4 结语

在现代化的多媒体教室和功能强大的Mathematica软件的帮助下，传统的经济数学教学过程中出现的一些诸如概念与定理难以理解、计算过程过于复杂等情况都得到了明显的改善，同时在教学中利用Mathematica软件可以激发学生学习经济数学的兴趣和提高学生学习积极性与主动性，课堂教学效果得到了明显提高.

[1] 陈卫忠，杨晓华. 经济数学(一)[M]. 苏州：苏州大学出版社，2012.

[2] 陈剑，王庆. 经济数学(二)[M]. 苏州：苏州大学出版社，2012.

[3] 吴肇基. 应用微积分[M]. 南京：东南大学出版社，2005.

[4] 马敏，冯梅. 经济应用数学[M]. 苏州：苏州大学出版社，2007.

[5] 白杰，李瑞勤. 高等数学中学生数学能力培养[J]. 长春大学学报：自然科学版，2012，22（12）：1501-1503.

[6] 丁大正. Mathematica5在大学数学课程中的应用[M]. 北京：电子工业出版社，2006.

(责任编辑：沈凤英)

Enhancing the Teaching Effect of Economic Mathematics by Mathematica Software

LU Wei-feng
(Department of Mathematics and Physics，Suzhou Vocational University，Suzhou 215104，China)

This paper describes some problems with theories and calculations in the teaching of economic mathematics.By using Mathematica software and multimedia tools，these problems can be solved，and the teaching effect can be enhanced remarkably.

economic mathematics；Mathematica software；teaching effect

G718.5

A

1008-5475(2015)03-0074-04

2015-04-16；

2015-05-14

陆卫丰(1977-)，男，江苏苏州人，讲师，主要从事应用数学教学研究.