基于B-(C,α)-I型广义凸多目标优化问题的充分条件

李 娜，贺 莉

(长春工业大学基础科学学院，吉林长春 130012)

基于B-(C,α)-I型广义凸多目标优化问题的充分条件

李 娜，贺 莉

(长春工业大学基础科学学院，吉林长春 130012)

本文给出了B-(C,α)-I型广义凸函数和伪拟、强伪拟、弱严格伪拟B-(C,α)-I型广义凸函数的定义，讨论了伪拟、强伪拟、弱严格伪拟B-(C,α)-I型广义凸函数间的关系,并基于此探讨了一类非光滑多目标优化问题的有效解和弱有效解的最优性充分条件。

B-(C,α)-Ⅰ型广义凸函数；最优性充分条件；多目标优化

为了减弱对凸性的要求，许多学者推广了众多广义凸函数类[1-5].Yuan[2]推广了(F,α,ρ,d)广义凸函数，给出了广义凸函数(C,α,ρ,d)的定义.Yuan[3]定义了(C,α,ρ,d)-I型广义凸函数，并给出了最优性条件.

本文给出了B-(C,α)-I型广义凸函数和伪拟、强伪拟、弱严格伪拟B-(C,α)-I型广义凸函数的定义，并讨论了它们之间的关系.在此基础上，我们探讨了一类非光滑多目标优化问题的有效解和弱有效解的最优性充分条件.

本文考虑下面多目标优化问题：

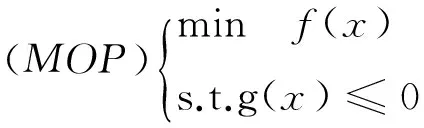
其中，X⊂Rn是非空开集，f:Rn→Rp,g:Rn→Rm,J(x)={j|gj(x)=0}.

1 预备知识

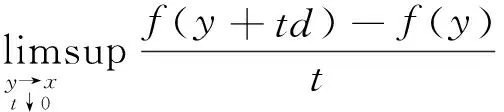
并记f在x处广义次梯度为∂f(x)={η∈Rn|f0(x;d)≥〈η,d〉,d∈Rn}.

定义3[3]设X是Rn中非空开集，若对任意固定的(x,y)∈Rn×Rn，∀λ∈(0,1)，∀z1,z2∈Rn,有C(x,y;λz1+(1-λ)z2)≤λC(x,y;z1)+(1-λ)C(x,y;z2)，则称函数C:X×X×Rn→R在Rn上是关于第三个变量的凸泛函.

注 特殊地，若λ=0时，则C(x,y;λz)=0,z∈Rn.

本文采用下列记号：

α:X×X→R+{0},d:X×X→R+,u=(u1,u2,…，up),v=(v1,v2，…，vm)，

C(x,x0;α(x,x0)ξ):=(C(x,x0;α(x,x0)ξ1),…，C(x,x0;α(x,x0)ξp))T，

C(x,x0;α(x,x0)ζ):=(C(x,x0;α(x,x0)ζ1),…,C(x,x0;α(x,x0)ζm))T，

ξ∈∂fi(x0),i∈{1,2,…,p},ζj∈∂gj(x0),j∈{1,2，…，m}.

2 主要结果

定义4 若(f,g)在x0∈X处是局部李普希兹函数，对任意x∈X，有下列式子：

b1(x,x0)(f(x)-f(x0))C(x,x0;α(x,x0)ξ)+d2(x,x0)ρ(1).

(1)

-b2(x,x0)g(x0)C(x,x0;α(x,x0)ζ)+d2(x,x0)ρ(2).

(2)

成立，则称(f,g)在x0∈X处是B-(C,α)-I型凸的.

若(f,g)在X的任意点为B-(C,α)-I型凸的，则称(f,g)为X上的B-(C,a)-I型广义凸函数.

注 特别地，当b1(x,x0)=b2(x,x0)=1时，B-(C,α)-I型广义凸函数退化为(C,α,ρ,d)-I型广义凸函数，因此B-(C,α)-I型广义凸函数扩大了凸函数的范围.下面的数值例子进一步说明了这一点.

例1:设X=(-1,1]

易知，可行域X0=[0,1]，∂f1(0)=[0,1]，∂f2(0)=[0,2],∂g(0)={0}，

令C(x,x0;α(x,x0)ξ)=|α(x,x0)ξ|(x+x0),C(x,x0;α(x,x0)ζ)=|α(x,x0)ζ|(x+x0),

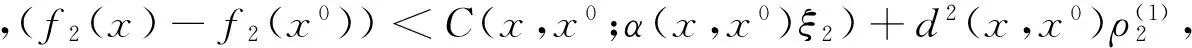
因此，(f,g)在x0=0处不是(C,α,ρ,d)-I型广义凸的.

定义5 若(f,g)在x0∈X处是局部李普希兹函数，且满足下面式子：

b1(x,x0)(f(x)-f(x0))<0⟹C(x,x0;α(x,x0)ξ)+d2(x,x0)ρ(1)<0,

(3)

-b2(x,x0)g(x0)≦0⟹C(x,x0;α(x,x0)ζ)+d2(x,x0)ρ(2)≦0.

(4)

则称(f,g)在x0∈X处是伪拟B-(C,α)-Ι型凸的.

定义6 若(f,g)在x0∈X处是局部李普希兹函数，且满足下面式子：

b1(x,x0)(f(x)-f(x0))≤0⟹C(x,x0;α(x,x0)ξ)+d2(x,x0)ρ(1)<0,

(5)

-b2(x,x0)g(x0)≦0⟹C(x,x0;α(x,x0)ζ)+d2(x,x0)ρ(2)≦0.

(6)

则称(f,g)在x0∈X处是弱严格伪拟B-(C,α)-I型凸的.

定义7 若(f,g)在x0∈X处是局部李普希兹函数，且满足下面式子：

b1(x,x0)(f(x)-f(x0))≤0⟹C(x,x0;α(x,x0)ξ)+d2(x,x0)ρ(1)≤0,

(7)

-b2(x,x0)g(x0)≦0⟹C(x,x0;α(x,x0)ζ)+d2(x,x0)ρ(2)≦0.

(8)

则称(f,g)在x0∈X处是强伪拟B-(C,α)-I型凸的.

注 由上述定义可知，如果(f,g)在x0∈X是强伪拟B-(C,α)-I型凸的，则一定为弱严格伪拟B-(C,α)-I型凸的；如果(f,g)在x0∈X是弱严格伪拟B-(C,α)-I型凸的，则一定为伪拟B-(C,α)-I型凸的，反之，则不成立.

基于上面讨论的B-(C,α)-I型广义凸函数，建立非光滑多目标规划问题(MOP)的最优性条件.

证明:假设x0不是(MOP)问题的有效解，那么存在x*∈X，使得

fi(x*)-fi(x0)≤0,i∈{1,2,…,p}，且至少存在一个i0∈{1,2，…，p}，使不等式严格成立.

因bk:X×X→R+，所以b1(x*,x0)(fi(x*)-fi(x0))≤0,i∈{1,2，…，p}，

-b2(x*,x0)gj(x0)≦0，j∈J，

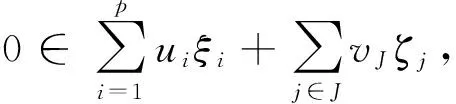
注 将定理1中的凸性条件改为(f,g)在x0∈X是弱严格伪拟B-(C,α)-I型凸的，且u≥0,v≥0，充分性仍然成立.

定理2 设x0∈X是(MOP)问题的可行解，如果满足:

证明:假设x0不是(MOP)问题弱有效解，那么存在x*∈X，使得

fi(x*)-fi(x0)<0,i∈{1,2，…，p},

因bk:X×X→R+,b1(x*,x0)(fi(x*)-fi(x0))<0,i∈{1,2，…，p}，

-b2(x*,x0)gj(x0))x0≦0，j∈J，

定理2其余的证明类似于定理1的证明.

注 将定理2中的条件(2)改为下列条件之一，充分性仍成立.

(i)(f,g)在x0∈X为强伪拟B-(C,α)-I型凸的，且u>0，v≥0；

(ii)(f,g)在x0∈X为弱严格伪拟B-(C,α)-I型凸的.

[1]Hanson,M.A.,andMond,B.Necessaryandsufficientconditionsinconditionsinconstrainedoptimization[J].Math.Program.,1987(37):51-58.

[2]Yuan,D.H.,Liu,X.L.,Chinchuluun,A.,andPardalos,P.M.Nondifferentiableminimaxfractionalprogrammingproblemswith(C;a;r;d)-convexity[J].J.Optim.TheoryAppl.,2006,129(1):185-199.

[3]Yuan,D.H.,Liu,X.L.,Chinchuluun,A.,andPardalos,P.M.OptimalityConditionsandDualityforMultiobjectiveProgrammingInvolving(C,α,ρ,d)type-IFunctions[J].J.Glob.Optim.,2006(583):73-87.

[4]Long,X.Optimalityconditionsanddualityfordifferentiablemultiobjectivefrac-tionalprogrammingproblemswith(C;a;r;d)-convexity[J].J.Optim.TheoryAppl.,2011,148(1):197-208.

[5]RekhaGupta,M.Srivastava.OptimalityanddualityfornonsmoothmultiobjectiveprogrammingusingG-typeIfunctions[J].AppliedMathematicsandComputation,2014(240):294-307.

[6]林锉云,董加礼.多目标优化的方法与理论[M].吉林:吉林教育出版社,1992.

Optimality Conditions for a Multiobjective Programming Problem under GeneralizedB-(C,α)- typeIUnivex Functions

LI Na，HE Li

(School of Basic Science, Changchun University of Technology, Changchun Jilin 130012, China)

In this paper, we introduce the definition of a new generalized class ofB-(C,α)- typeIunivex functions, and pseudo- quasi, strong pseudo-quasi, weak strictly quasi-pseudoB-(C,α)- typeIunivex functions, discusse the relationship between them, and establish sufficient optimality conditions for a nonsmooth multiobjective programming.

B-(C,α)- typeIunivex functions; optimality conditions; multiobjective programming

2015-01-15

吉林省自然科学基金项目(20130101061JC)。

李 娜(1981-)，女，河南南阳人，长春工业大学基础科学学院硕士研究生，从事最优化理论与算法研究。

贺 莉(1970-)，女，吉林图们人，副教授，硕士生导师，从事最优化理论与算法研究。

O221

A

2095-7602(2015)04-0001-04