广义G-矩阵

马培兰

(伊犁师范学院数学与统计学院，新疆伊宁 835000)

广义G-矩阵

马培兰

(伊犁师范学院数学与统计学院，新疆伊宁 835000)

本文从广义G-矩阵的定义出发，利用矩阵的广义Schur-补，讨论了广义G-矩阵的充要条件。

广义逆矩阵；广义G-矩阵；Schur-补

文献[2]中定义了广义G-矩阵,并讨论了几种特殊形式的G-矩阵.文献[3-4]中对G-矩阵及广义G-矩阵进行了进一步的讨论.在文献[5-6]中讨论了矩阵的广义Schur-补的最大最小秩.本文利用矩阵的广义Schur-补的最大最小秩，从另一个角度讨论了广义G-矩阵的充要条件.

定义1.1[1]设矩阵A∈Rm×n，如果矩阵X满足下列矩阵方程中的一个或几个：(1)AXA=A；(2)XAX=X；(3)(AX)T=AX；(4)(XA)T=XA，则称矩阵X∈Rn×m为矩阵A的广义逆.

对于集合{1,2,3,4}的子集{i,j,…}，n×m矩阵X称为矩阵A的{i,j,…}-逆.如果它满足方程(i),(j),(k)，记为A(i,j,k).矩阵A的{i,j,…}-逆的全体构成的集合记为A{i,j,k}.

矩阵的{1}-逆也称为g-逆，{1,3}-逆也称为最小二乘g-逆.

1 引言

定义1.2[2]设矩阵A∈Rn×n，如果A非奇异并且存在非奇异对角矩阵D1，D2，使得(AT)-1=D1AD2，则称A为G-矩阵.

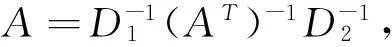
定义1.3 设矩阵A∈Rmxn，如果存在非奇异对角矩阵D1∈Rm×m,D2∈Rn×n,使得A=D1(AT)+D2，则称为广义G-矩阵.

定义1.4 设矩阵A∈Rm×n,如果存在非奇异对角矩阵D1∈Rm×m,D2∈Rn×n,A(i,j,k)∈A{i,j,k},使得A=D1(AT)(i,j,k)D2,则称A为广义G(i,j,k)-矩阵.

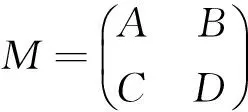
(1)若A为非奇异矩阵，则A在M中的Schur补为SA=D-CA-1B，并且

rank(M)=rank(A)+rank(D-CA-1B).

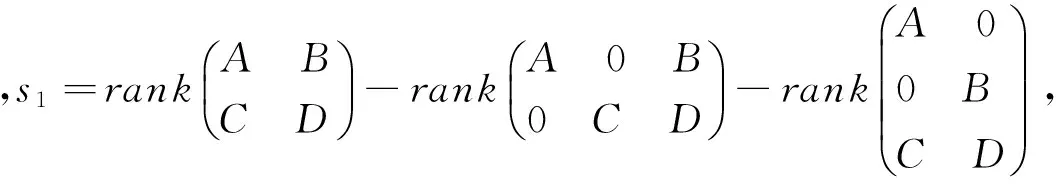
2 关于广义G-矩阵的结论

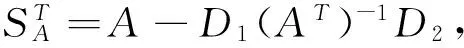
且rank(M)=rank(AT)+rank(A-D1(AT)-1D2)=rank(A)+rank(A-D1(AT)-1D2).

因此，矩阵A为G-矩阵

⟺A=D1(AT)-1D2⟺A-D1(AT)-1D2=0⟺rank(A-D1(AT)-1D2)=0

⟺rank(M)=rank(A)+rank(A-D1(AT)-1D2)=rank(A).

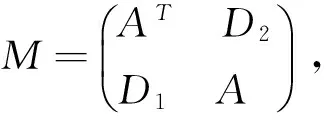
rank(A-D1(AT)+D2)

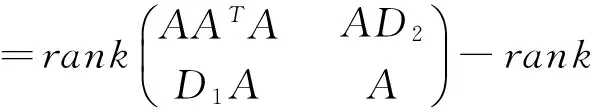
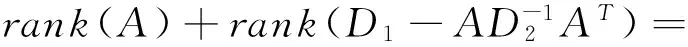
证明 由定义1.4知，A为广义G(1)-矩阵时，存在非奇异对角矩阵D1∈Rm×m，D2∈Rn×n，A(1)∈A{1},使得A=D1(AT)(1)D2，即A-D1(AT)(1)D2=0.

而由引理1.5知

minrank(A-D1(AT)(1)D2)

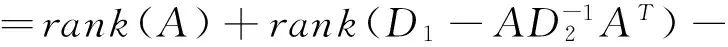
因此，矩阵A为广义G(1)-矩阵

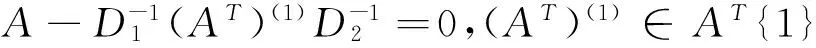
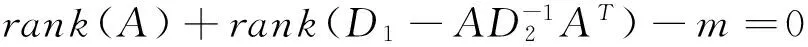
定理2.4 设矩阵A∈Rm×n，则矩阵A为广义G(1,2)-矩阵的充分必要条件是存在非奇异对角矩阵D1∈Rm×m，D2∈Rn×n，使得rank(A)+m+n+max{s1,s2}=0，其中

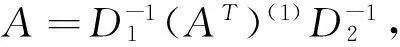
而由引理1.5知

minrank(A-D1A(1,2)D2)

=m+n+rank(A)+max{s1,s2}.

其中

因此，矩阵A为广义G(1,2)-矩阵

⟺m+n+rank(A)+max{s1,s2}=0.

[1]A.Ben-Israel,T.N.E.Greville.GeneralizedInverse:TheoryandApplications[M].Seconded.,Springer-Verlag,NewYork,2002.

[2]G-matrix[J].LinearAlgebraAppl.,2012,436:731-741.

[3]MiroslavFiedler,ThomasL.Markham,MoreonG-matrices[J].LinearAlgebraAppl.,2013,438:231-234.

[4]MasayaMatsuura.AnoteongeneralizedG-matrices[J].LinearAlgebraAppl.,2012,436:3475-3479.

[5]YonggeTian.MoreonmaximalandminimalranksofSchurcomplementswithapplications[J].AppliedMathematicsandComputation,2004,152:675-692.

[6]YonggeTian.Upperandlowerboundsforranksofmatrixexpressionsusinggeneralizedinverses[J].LinearAlgebraAppl.,2002,355:187-214.

Generalized G-matrices

MA Pei-lan

(School Mathematics and Statistics，Yili Normal University，Yining Xinjiang 835000，China)

From the definition of generalized G-matrices, using the generalized Schur-complement discuss the the necessary and sufficient conditions for generalized G-matrices.

generalized inverse；generalized G-matrices；Schur-complement

2015-01-20

马培兰(1987-)，女，河南偃师人，伊犁师范学院数学与统计学院助教，硕士，从事计算数学研究。

O154

A

2095-7602(2015)04-0009-03