点集拓扑教学中几个反例的运用
张 婧
(伊犁师范学院数学与统计学院,新疆伊宁 835000)
点集拓扑教学中几个反例的运用
张 婧
(伊犁师范学院数学与统计学院,新疆伊宁 835000)
在点集拓扑教学中通过对几个典型反例的阐述和运用,能够加强学生对基本概念和定理的理解,有利于学生理解和掌握证明过程中所蕴含的一些重要方法,提高学生分析问题和解决问题的能力。
反例;拓扑空间;公理
点集拓扑学是用公理化方法研究抽象空间性质的学科.所谓公理化方法是从少数原始概念和若干无矛盾的公理出发运用严密的逻辑推理建立理论体系的方法.因此,点集拓扑学与近代数学的其他分支一样是一门抽象程度较高的学科.学好这门课需要较强的抽象思维能力,这恰恰是大多数学生觉得困难的地方.通过对课程中一些典型问题的分析研讨,可以使学生更牢固地掌握数学的思想方法并具备初步进行数学理论研究的能力.在教学中适当地构造反例,通过反例使学生掌握点集拓扑学中的概念本质,简明地说明概念间相互的联系与差异,能够使学生真正掌握概念,为修正学生对知识理解中出现的错误提供帮助.
1 点集
学习点集拓扑,首先应清楚拓扑空间中各类集合的定义及集合之间的关系,例如拓扑空间中的导集、闭集以及二者之间的关系.
定义1 设X是一个拓扑空间,A⊂X.如果点x∈X的每一个邻域U中都有A中异于x的点,即U∩(A-{x})≠∅,则称点x是集合A的一个凝聚点或极限点.集合A的所有凝聚点构成的集合称为导集,记作d(A).
定义2 设X是一个拓扑空间,A⊂X.如果A的每一个凝聚点都属于A,即d(A)⊂A,则称A是拓扑空间X中的一个闭集.
在数学分析中配备了由欧式空间上通常的度量所诱导出来的拓扑,就成为一个拓扑空间.对这个拓扑空间中的集合性质学生相对更加熟悉,但却容易限定一般拓扑空间中集合的性质.在欧式度量空间内,有限集的导集必是空集,但在一般的拓扑空间内有限集的导集不必是空集.另外,在欧式度量空间中,一个集的导集必为闭集,而在一般的拓扑空间内,一个集的导集未必是闭集.下面仅就这两种情况举出反例.
例1 存在某个有限集合,其导集非空.
设X={x1,x2,x3},令τ={X,{x1,x2},{x1,x3},{x1},∅},则(X,τ)为一个拓扑空间,考虑X的子集A={x1},则点x2和x3是A的凝聚点.故d(A)={x2,x3},即有限集A的导集d(A)非空.
例2 存在某个集合的导集不是闭集.
设X={x1,x2,x3},令τ={X,{x2,x3},{x1},∅},则(X,τ)为一个拓扑空间.取A={x2},易见d(A)={x3}且d(A)不是闭集.
2 同胚映射
拓扑学的中心任务是研究拓扑不变性质.所谓拓扑不变性质即为同胚的拓扑空间所共有的性质.而说明两个拓扑空间是不是同胚的,恰恰就是看两个空间之间是否存在一个同胚映射.因而,同胚映射在拓扑学中是很重要的概念.
定义3 设X和Y是两个拓扑空间,如果f:X→Y是一个一一映射,并且f和f-:Y→X都是连续的,则称f是一个同胚映射或同胚.
此定义要求的条件比较强,既要求f是连续的一一映射,同时要求f-也是连续的,这些条件是不能蕴含的,为此我们给出一个例子说明即便是连续的一一映射,其逆映射也可以不是连续的.

3 分离性公理
由拓扑空间的分离性公理,我们定义了T0,T1,T2,T3,T4空间(具体定义参见文献[1]),满足分离性的这五种拓扑空间之间有如下关系:T4⟹T3⟹T2⟹T1⟹T0,关于反方向蕴含不成立的反例在此一一给出.
例4 存在T0而非T1的拓扑空间.
设X={x1,x2,x3},令τ={X,{x1,x2},{x1,x3},{x1},∅},则(X,τ)为一个拓扑空间.易见,X是T0空间.因为对于点x1,x3而言,含点x3的开集必含有点x1,所以X不是T1空间.
例5 存在T1而非T2的拓扑空间.
设X为一不可数集,规定X上的拓扑为:X的闭子集族由X的至多可数子集连同X组成.易见,X是T1且X中任何两个点都不能被开集分离,因而X不是T2空间.
例6 存在T2的非正则也非正规的空间.
Niemytzki平面.设X⊂R2,X={(x,y)|y≥0},令R为x轴,在X引进如下拓扑基:

其中,B(P,ε)是R2中按欧式度量以P为中心、ε为半径的开球.称V(P,ε)为P的标准邻域基元,则={V(P,ε)|ε>0,P∈X}是X上的一个拓扑基.事实上,我们不难验证,满足:
(1)X=UP∈XV(P,ε);
(2)∀V(P1,ε1),V(P2,ε2)∈,∀x∈V(P1,ε1)∩V(P2,ε2),必存在V(P,ε),使得
x∈V(P,ε)⊂V(p1,ε1)∩V(P2,ε2).对于∀P1,P2∈X,P1≠P2,取ε=ρ(P1,P2),则

下面说明(X,τ)不是正则的,也不是正规的.由拓扑基构造知,x轴上任意子集是闭集.取点θ=(0,0),闭集F=R/{θ}.
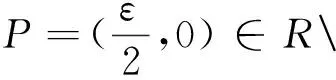

又因为F*={θ}是闭集,F∩F*=∅,故∀U∈U(θ)=U(F*),∀W∈U(F)同上所证,有U∩W≠∅.所以(X,τ)也不是正规的.
4 拓扑空间中紧集与闭集
在紧的Hausdorff空间中每一个紧子集都是闭集,因而在紧的Hausdorff空间中两个紧子集的交还是紧集.然而在一般的拓扑空间中这点是不一定成立的.
例7 存在某个拓扑空间中两个紧集,其交不是紧集.
设Y是实数集并取通常拓扑,Z是点集{0,1}并取平庸拓扑,X=Y×Z取乘积拓扑.令A={[a,b]×{0}}∪{(a,b)×{1}},B={(a,b)×{0}}∪{[a,b]×{1}}.
需要注意的是,X的开集具有形式(c,d)×∅或(c,d)×{0,1}.因此,假若X的开集G含有点x=(y,0),那么G也一定含有点(y,1).

其次,A∩B不是紧的.因A∩B=(a,b)×{0,1},而(a,b)不是Y的紧子集,故A∩B也不是Y的紧子集.
5 结语
以上是笔者总结的常用反例,在教学实践中收到了较好的效果,对学生进一步理解概念和相关定理起到了促进作用,可以使学生澄清对某些概念和性质的模糊认识,也让他们意识到拓扑空间是要比之前在数学分析中讨论的度量空间更广泛的一个范畴。通过反例的构造和应用,将度量空间中熟识的一些概念和性质进一步一般化,使学生对点集拓扑课程有更深刻的理解,提高他们分析问题、解决问题的能力,最终达到培养学生创新能力的教学目的.
[1]熊金城.点集拓扑讲义[M].3版.北京:高等教育出版社,2003.
[2]朱培勇,雷银彬.拓扑学导论[M].北京:科学出版社,2009.
[3]汪林,杨富春.拓扑空间中的反例[M].北京:科学出版社,2000.
[4]邹应.拓扑学习题集[M].武昌:武汉大学出版社,2003.
[5]陈肇姜.点集拓扑学题解与反例[M].南京:南京大学出版社,1997.
2015-01-02
伊犁师范学院一般科研项目(2013YSYB18)。
张 婧(1980- ),女,山东济宁人,伊犁师范学院数学与统计学院讲师,博士研究生,从事调和分析研究。
O189;G642
A
2095-7602(2015)04-0017-03

