改进的核空间直觉模糊C-均值聚类分割算法

田小平, 侯伟建, 吴成茂

(西安邮电大学 电子工程学院,陕西 西安 710121)

改进的核空间直觉模糊C-均值聚类分割算法

田小平, 侯伟建, 吴成茂

(西安邮电大学 电子工程学院,陕西 西安 710121)

针对鲁棒模糊局部信息C-均值聚类分割算法易丢失图像细节的问题,提出一种改进的核空间直觉模糊C-均值聚类算法。将像素空间邻域信息和直觉指数引入到鲁棒模糊局部信息C-均值聚类目标函数,给出改进的像素空间邻域信息约束的聚类目标函数,对其聚类目标函数最优化推导并得到新的隶属度和聚类中心迭代表达式,并设计相应的图像分割算法,以便提高图像局部信息的有效分割能力。实验结果表明,改进的核空间直觉模糊聚类分割算法相比现有鲁棒模糊局部信息C-均值聚类分割算法能获得更好的分割效果。

模糊C-均值聚类；像素空间邻域信息；核空间；直觉模糊集

模糊集理论最初由Bezdek于1965年提出[1],并在各个领域均得到了成功的应用。而模糊C均值(Fuzzy C-means,FCM)聚类算法[2]是基于目标函数的模糊聚类算法,因其算法简单,收敛速度快而得到广泛应用,但该算法没有考虑像素的邻域信息,同时单一的隶属度无法充分的描述图像的不确定性,使其对噪声比较敏感且不适合小目标图像的分割需要。因此具有一定抗噪性的二维或三维直方图上的快速模糊聚类分割算法[3-4]和空间信息约束的改进模糊C-均值聚类分割算法[5-12]相继提出。文献[13]提出的邻域直觉模糊C-均值(Neighborhood Intuitionistic Fuzzy C-means,NIFCM)算法,通过对隶属度引入空间邻域信息和直觉模糊集[14](Intuitionistic Fuzzy Set,IFS),有效地提高了对图像细节部分的分割效果。

公茂果等[15]将聚类分割算法推广至核空间,并改进其像素与邻域像素之间的加权因子,获得一种具有一定普适性的鲁棒模糊局部C均值聚类(Fuzzy C-means Clustering with Fuzzy Weighted Factor and Kernel Metric,KWFLICM)算法,提高了对复杂医学、遥感图像分割的适应能力并能取得较满意的分割效果。这种改进算法虽抗噪性强,但难以描述图像信息的不确定性,对图像在细节处的分割处理不够细致,易丢失目标信息,对微小区域的分割不理想。针对KWFLICM算法的不足,结合NIFCM算法,通过加入IFS理论提出一种改进的核空间直觉模糊C-均值聚类算法(Improve Kernel Space Intuitionistic Fuzzy C-means Clustering Segmentation Algorithm,IFILICM)。通过引入非隶属度和犹豫度来考虑图像信息的模糊性和不确定性。

1 FCM算法

FCM算法是基于对模糊目标函数的优化基础上的一种数据聚类方法,其目标函数表达式[2]为

(1)

其中X=(x1,x2,…,xn)是图像像素的灰度值之集,v=(v1,v2,…,vc)是区域的聚类中心之集,uki表示xi属于第k类区域的隶属度,vk表示第k类的聚类中心,m为模糊加权指数。式(1)满足如下约束条件

利用拉格朗日乘子法求得隶属度uki和聚类中心vk的迭代更新表达式为

(2)

(3)

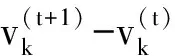
2 直觉模糊集和直觉模糊熵

2.1 直觉模糊集

Atanassov对直觉模糊集给出如下定义[14]。

设X是一个给定论域,则X上的一个直觉模糊集A为

A={|x∈X}

式中μA(x)∶X→[0,1]和vA(x)∶X→[0,1],分别代表A中元素x属于A的隶属度和非隶属度,且对于所有的x∈X,有0≤μA(x)+vA(x)≤1。

直觉模糊集可定义为A={|x∈X},即当vA(x)=1-μA(x)时,直觉模糊集退化为一般模糊集。

对于X上的每一个直觉模糊子集,称πA(x)=1-μA(x)-vA(x)为A中x的直觉指数,它是x对A的犹豫程度的一种测度,称为犹豫因子。对于每一个x∈X,有0≤πA(x)≤1。

显然,对于X上的一般模糊子集A,πA(x)=0,∀x∈X。因此,准确地描述一个直觉模糊集就需要从隶属度函数、非隶属度函数和犹豫度三方面来说明。相比传统的模糊集在处理模糊性和不确定性等方面的问题时,表现出了更强的灵活性和实用性。

关于直觉模糊集,其非隶属度函数的生成通常采用Yager生成函数,其表达式为[14]

N(μ(x))=g-1(g(l)-g(μ(x))),

式中g(·)是一个单调递增的函数,满足g∶[0,1]→[0,1]。在实际应用中,通常被定义为

g(x)=xα。

所以非隶属度函数的表达式为

N(x)=(1-xα)1/α,α>0,

式中N(1)=0,N(0)=1,因此,IFSs表达式为

A={|x∈E},

则相应的犹豫度定义为

πA(x)=1-μA(x)-(1-μA(x)α)1/α。

(4)

2.2 直觉模糊熵

直觉模糊信息熵[16]是为了更好的对直觉模糊集[17]的不确定性进行描述。直觉模糊集

A={|x∈X}

的熵H(A)是一个实值函数,H∶H(A)→[0,1],满足以下4个公理。

(1)H(A)=0,当且仅当A是一个经典集合。

(2)H(A)=1,当且仅当对于xi∈X,有μA(x)=vA(x)。

(3) 如果A⟸B,μA(x)≤μB(x),vA(x)≤vB(x),则πA(x)≥πB(x)和H(A)≥H(B)。

(4)H(A)=H(Ac)

其中

Pi=μA(xi)lnμA(xi)+vA(xi)lnvA(xi)-

(1-πA(xi))ln(1-πA(xi))-πA(xi)ln2,

当πA(xi)=0,直觉模糊熵就退化为模糊熵。

3 NIFCM算法

NIFCM算法的目标函数表达形式为[13]

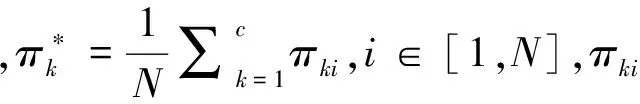
(5)

(6)

(7)

式中S代表邻域像素,如图1所示。聚类性能受S的影响,S越大越容易导致过度拟合的现象,在医学图像的处理方面无法有效的协助医生进行诊断。

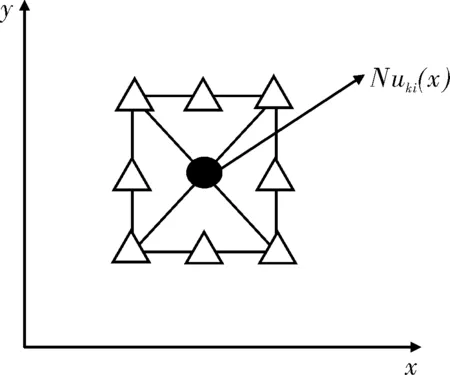
图1 邻域的定义

4 KWFLICM算法

KWFLICM算法的目标函数的表达形式为[15]

(8)

(9)

(10)

其中

模糊权重因子的表达式为

(11)

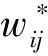
(12)

(13)

其中

可以看出KWFLICM算法对噪声干扰图像有很好的抗噪性,但其难以度量图像信息的不确定性,对微小区域的分割不理想。

5 IFILICM算法

IFILICM算法充分考虑图像的不确定性,在KWFLICM算法目标函数的基础上引入空间邻域信息、犹豫度,其目标函数的表达形式为

(14)

其中

式中Nuki采用式(6),则调整隶属度和聚类中心的表达形式分别为

(15)

(16)

其中

(17)

uki为文献[15]中的隶属度。

算法的过程为以下7个步骤。

步骤1确定聚类数目c(2≤c≤n),模糊指数m,Yager直觉模糊指数α,窗口大小Ni,设定终止迭代条件阈值ε和最大迭代次数。

步骤2初始化聚类中心,采用FCM算法的聚类中心作为改进型核空间直觉模糊C-均值聚类分割的聚类中心。

步骤3初始化迭代计数器b=0；利用式(11)计算权重因子wij值。

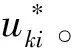
步骤5计算调整隶属度Nuki,待聚类中心更新后按式(15)更新Nuki。

步骤6根据式(16)更新聚类中心v。

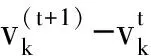
6 实验结果及分析

在实验测试环境为MATLAB7.0,算法参数选取模糊因子m=2,直觉模糊参数α=0.7,迭代误差ε=0.01,最大迭代次数Tm=500的条件下,分别对医学图像和复杂遥感图像(图2)进行了分割实验。其中α=0.7是由实验所得到的一个经验值。分别在无噪和加噪条件下对IFILICM算法与KWFLICM算法进行测试,比较这两种算法的分割性能。

6.1 无噪分割测试

人工将人类脑部CT图像分为3类进行分割实验,如图2(a)～图2(c)所示,分割结果分别如图3和图4所示。

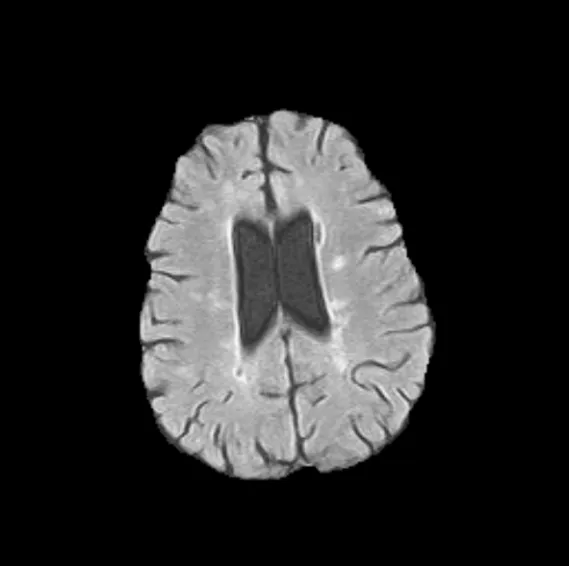
(a) 人类脑部CT1

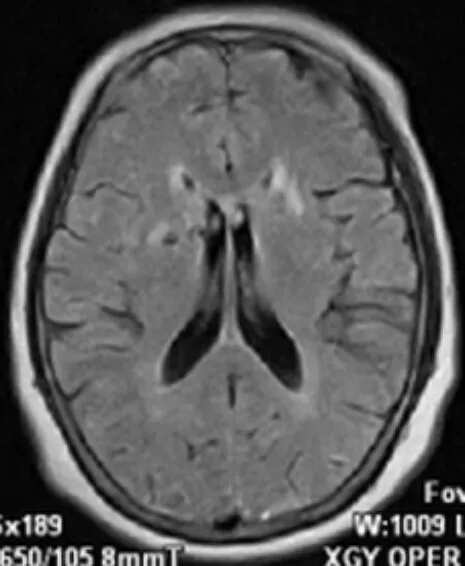
(b) 人类脑部CT2

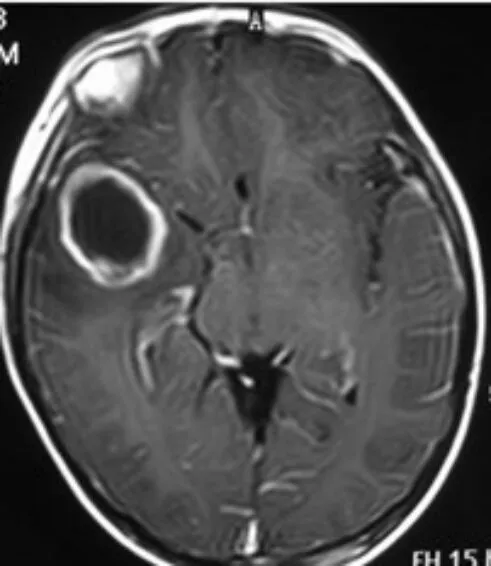
(c) 脑脓肿CT

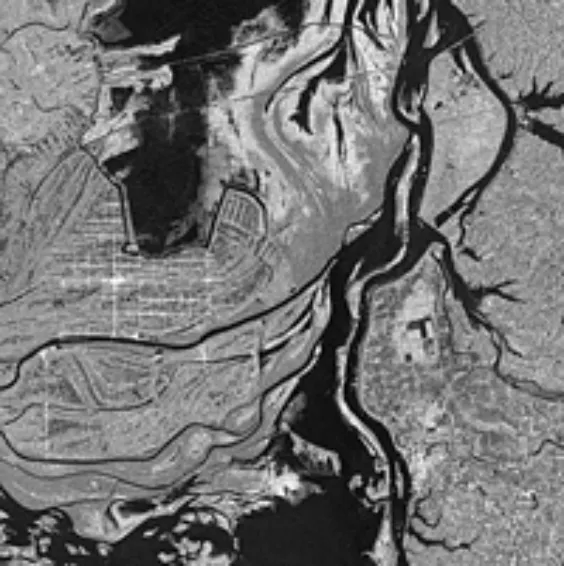
(d) 遥感河流1

(e) 遥感河流2

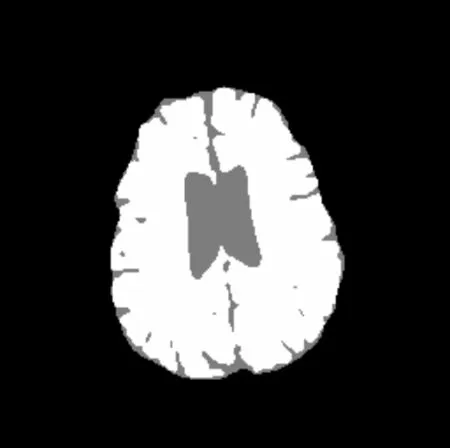
(a) 人类脑部CT1

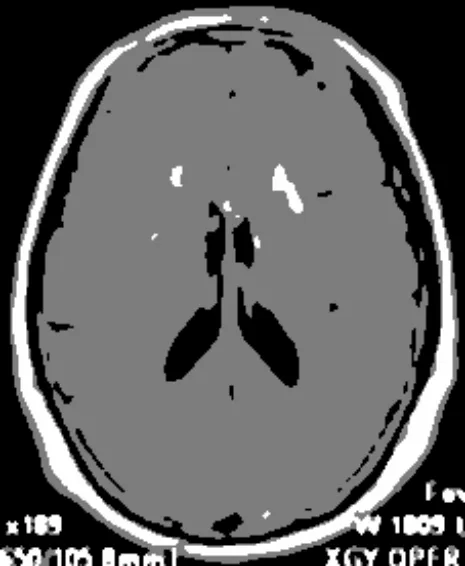
(b) 人类脑部CT2

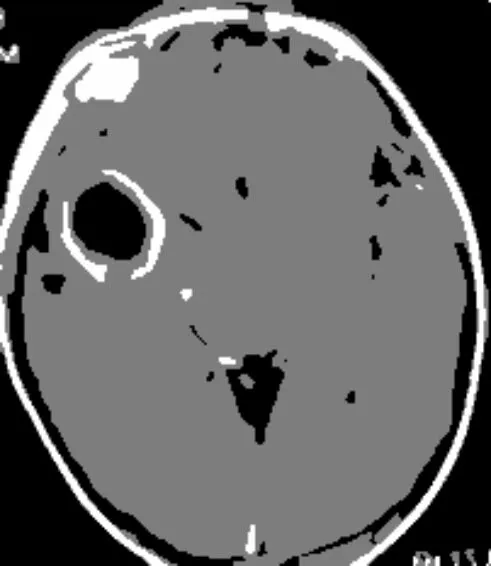
(c) 脑脓肿CT

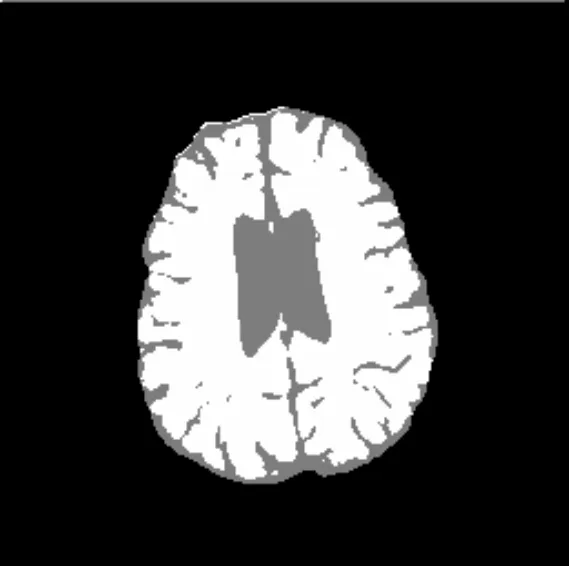
(a) 人类脑部CT1

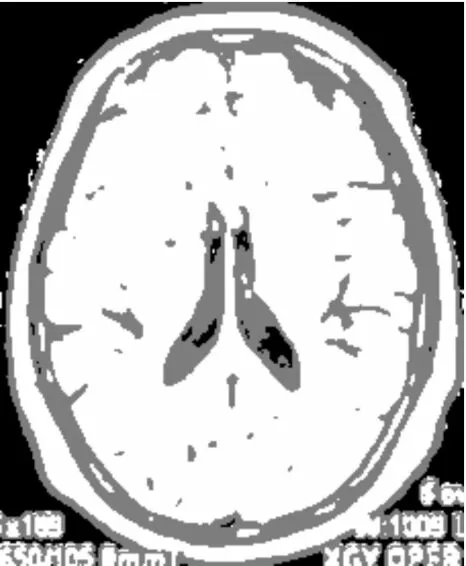
(b) 人类脑部CT2

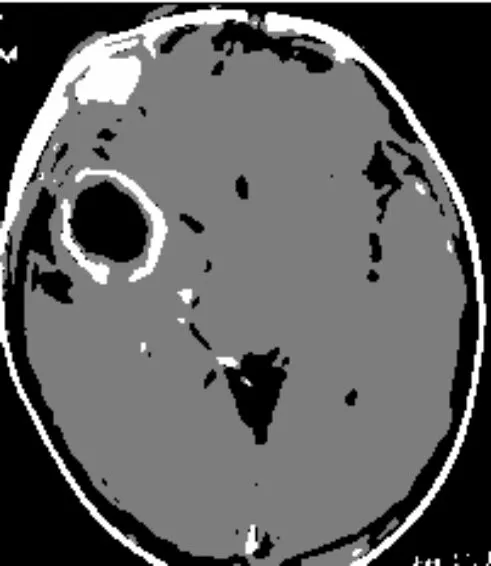
(c) 脑脓肿CT

从图3、图4分割结果可以看出,IFILICM算法在对脑部CT的分割上具有更好的分割效果,相比KWFLICM算法在对大脑皮层方面的处理上更加细致,在对脑核的分割上保留信息更加完整,在对脑脓肿CT图像的分割上更有效地保留病症的信息,KWFLICM算法对信息丢失的情况稍显严重,不利于协助医生诊断。显然,在对医学图像的处理上,本文算法能够更好地分割出原始图像的信息。

将遥感河流图像分为两类进行分割实验,如图2(d)和图2(e)所示,分割结果分别如图5和图6所示。

(a) 遥感河流1

(b) 遥感河流2

(a) 遥感河流1

(b) 遥感河流2

从图5、图6分割结果标记部分显然可以看出,针对如图所示的复杂遥感图像,本文算法在对细节部分的处理上更加细致,KWFLICM算法丢失信息严重,对比可知,IFILICM算法在图像的局部细节处有较好的分割效果。

6.2 加噪分割测试

分别对图2(c)和图2(d)所示的人类脑部CT图像和遥感图像加入0.1的椒盐噪声和均方差为25的高斯噪声(图7)进行分割测试,分割结果分别如图8和图9所示。

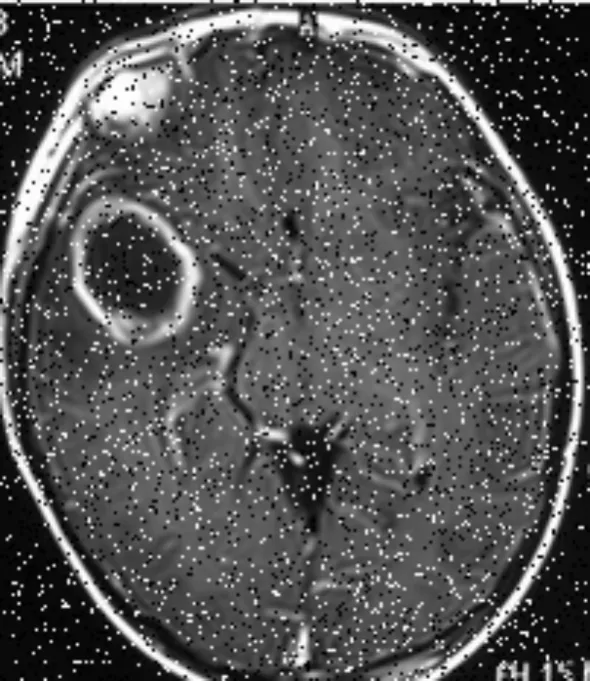
(a) 脑脓肿CT0.1椒盐噪声

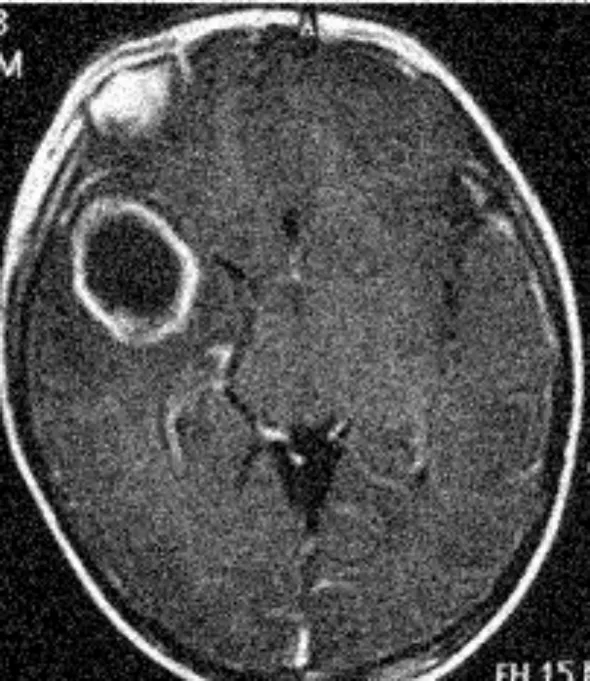
(b) 脑脓肿CT均方差为25的高斯噪声

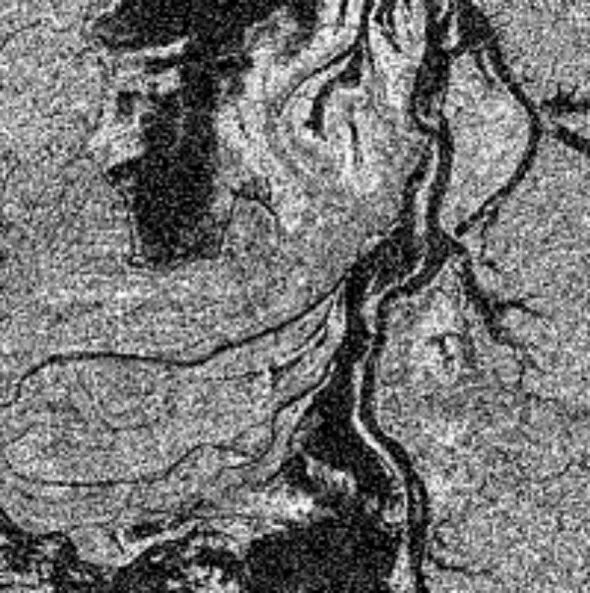
(a) 遥感河流10.1椒盐噪声

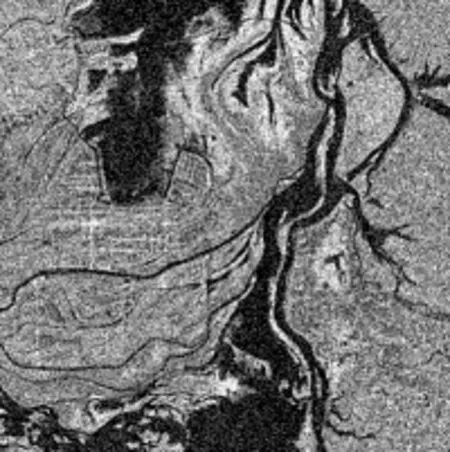
(b) 遥感河流1均方差为25的高斯噪声

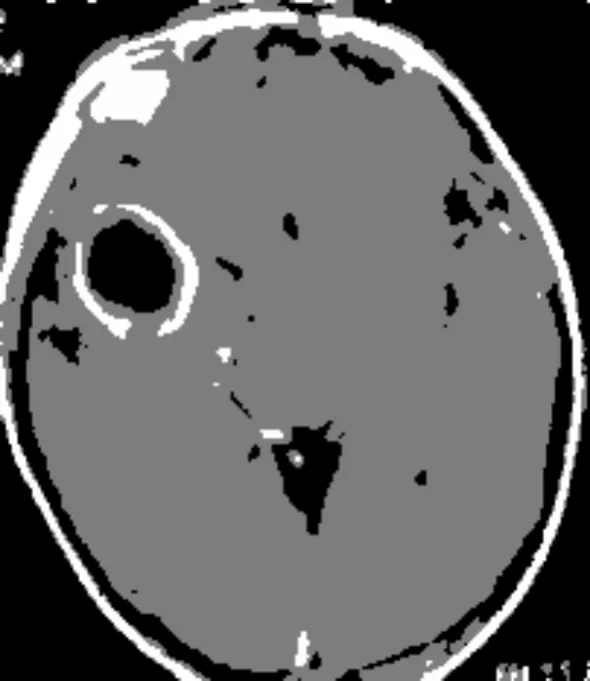
(a) 脑脓肿CT0.1椒盐噪声

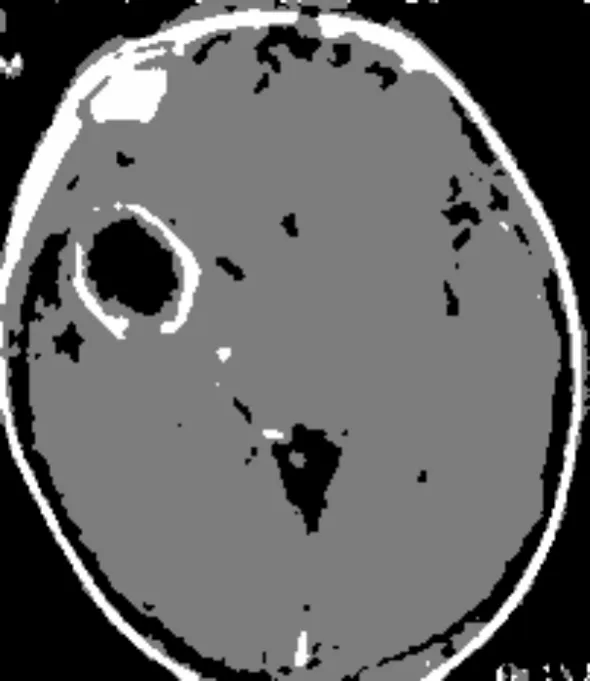
(b) 脑脓肿CT均方差为25的高斯噪声

(a) 遥感河流10.1椒盐噪声

(b) 遥感河流1均方差为25的高斯噪声

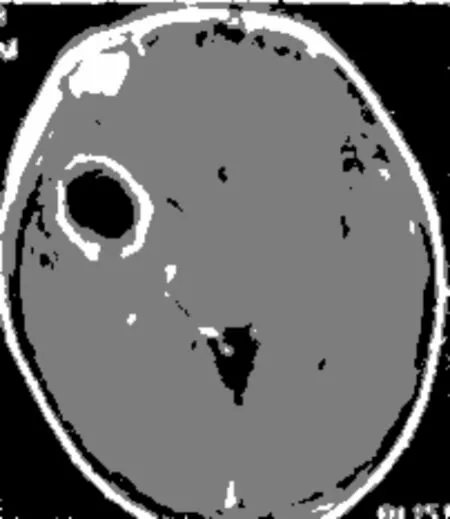
(a) 脑脓肿CT0.1椒盐噪声

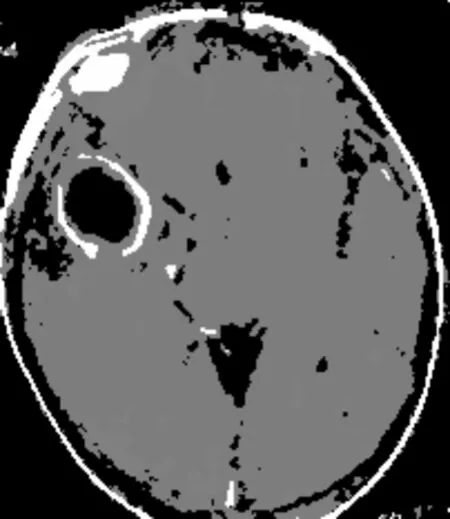
(b) 脑脓肿CT均方差为25的高斯噪声

(a) 遥感河流10.1椒盐噪声

(b) 遥感河流1均方差为25的高斯噪声

从图8和图9所示的两种聚类算法的分割结果来看,显然IFILICM算法较KWFLICM算法而言分割结果更为细致,可以得到更好的分割效果,更加适合小噪声干扰图像的分割需要。

7 结束语

综合考虑像素空间邻域信息和犹豫度对C均值聚类算法的影响,IFILICM算法在KWFLICM算法的基础上引入邻域像素信息,使得分割算法充分利用像素局部信息,在对图像的分割处理上更加细腻。实验结果表明采用核空间直觉模糊C-均值聚类算法对图像进行分割后所得图片与原始图像差异性较小,相比KWFLICM算法能对图像的细节信息更好的保留,更加准确地分割原始图像信息,得到更加有效的分割结果。在对医学图像分割处理上更加有效,能够提高医疗工作者对病患诊断的准确度。

[1] Zadeh L A.Fuzzy sets[J].Information and Control,1965,8(3)：338-356.

[2] Bezdek J C.Pattern Recognition with Fuzzy objective function algorithms[M]. New York: Plenum Press,1981:95-107.

[3] 刘健庄.基于二维直方图的图象模糊聚类分割方法[J].电子学报,1992,20(9):40-46.

[4] 吴成茂,张干.灰度级加权的直方图模糊熵阈值分割法 [J]. 西安邮电大学学报,2013,18(5):8-13.

[5] Krinidis S, Chatzis V. A robust fuzzy local information C-Means clustering algorithm.[J]. Image Processing IEEE Transactions on, 2010, 19(5):1328-1337.

[6] Celik T, Hk. L. Comments on “A Robust Fuzzy Local Information C-Means Clustering Algorithm”[J]. IEEE Transactions on Image Processing, 2013, 22(3):1258-1261.

[7] Liew A W C, Yan H. An adaptive spatial fuzzy clustering algorithm for 3-D MR image segmentation[J]. IEEE Trans on Medical Imaging,2003,22(9):1063-1075.

[8] Kim J N, Cai W D, Feng D G, et al. Segmentation of VOI From Multidimensional Dynamic PET Images by Integrating Spatial and Temporal Features[J]. IEEE Trans on Technology in Biomedicine,2006,10(4):637-646.

[9] Chen Songcan, Zhang Daoqiang. Robust image segmentation using FCM with spatial constraints based on new kernel-induced distance measure[J]. IEEE Trans on Systems, Man, and Cybernetics, Part B: Cybernetics,2004,34(4):1907-1916.

[10] 李琳,范九伦,赵凤.模糊C-均值聚类图像分割算法的一种改进[J].西安邮电大学学报,2014,15(5):56-60.

[11] Xiang Deliang, Hu Canbing, Li Yu, et al. A Kernel Clustering Algorithm With Fuzzy Factor Application to SAR Image Segmentation[J]. IEEE Geoscience and remote sensing letters,2014,11(7) :1290-1294 .

[12] Murugeswari M, Gayathri M. Tumor detection in MRI brain image segmentation using phase congruency modified fuzzy C-mean algorithm[J]. International Journal of Innovative Science, Engineering & Technology,2014,1(4):190-194.

[13] Huang Wenching,Lin Pingkuo,Wu Changming ,et al. Intuitionistic fuzzy c-means clustering algorithm with neighborhood attraction in segmenting medical image[J].Soft Computing,2014,22(5):1-12.

[14] Atanassov K. Intuitionistic Fuzzy Sets [J]. Fuzzy Sets and Systems, 1986, 20(1): 87-96.

[15] Gong Maoguo, Liang Yan, Shi Jiao, et al. Fuzzy c-means clustering with local information and kernel metric for image segmentation[J].IEEE Trans on Image Processing, 2013,22(2):573-584.

[16] Szmidt E, Kacprxyk J. Entropy for Intuitionstic Fuzzy Sets[J]. Fuzzy Sets and Systems, 2001,118(3):467-477.

[17] De Luca A,Termini S.A Definition of a Nonprobabilistic Entropy in the Setting of Fuzzy Sets Theory[J].Information and Control, 1972, 20 (4): 301-312.

[责任编辑：祝剑]

Improve kernel space intuitionistic fuzzy C-means clustering segmentation algorithm

TIAN Xiaoping, HOU Weijian, WU Chengmao

(School of Electronic Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121,China)

In view of the issues that an improve kernel space intuitionistic fuzzy C-means clustering segmentation algorithm is proposed in this paper to tackle the problem that the fuzzy c-means clustering with fuzzy weighted factor and kernel metric (KWFLICM) segmentation algorithm could not keep the image details well. By introducing the pixel spatial neighbor information and the hesitation degree into the objective function of the KWFLICM algorithm, a new pixel spatial neighbor information constraints clustering objective function is proposed. By optimizing the clustering objective function, the new clustering center and membership iterative expressions are obtained. The corresponding image segmentation algorithm is presented to improve the ability of effective segmentation of image local information. Experimental results demonstrate that it can get the better results than that of KWFLICM.

fuzzy C-means cluster, pixel spatial neighbor information, kernel space, intuitionistic fuzzy set

2014-12-26

国家自然科学基金重点资助项目(61136002);陕西省自然科学基金资助项目(2014JM8331,2014JQ5138)。

田小平 (1963-),男,教授,从事信号与信息处理技术研究。E-mail:xptian@xupt.edu.cn 侯伟建 (1990-),女,硕士研究生,研究方向为图像处理及其信息安全。E-mail:houweijian1226@163.com

10.13682/j.issn.2095-6533.2015.06.010

TP751.1

A

2095-6533(2015)06-0045-06