基于独立分量分析的电力线物联网去噪
孙友伟, 苏少华
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
基于独立分量分析的电力线物联网去噪
孙友伟, 苏少华
(西安邮电大学 通信与信息工程学院, 陕西 西安 710121)
为了降低电力线物联网通信中的噪声影响,使用松弛因子对盲源信号处理中的鲁棒性独立分量分析算法进行优化,并应用于电力线物联网中。通信接收端采用多路接收信号,使用预白化矩阵降低各路信号之间的相关性之后,再利用基于松弛因子优化的鲁棒性独立分量分析算法计算出分离矩阵,对多路信号分离,并通过判决从分离出的信号中找到传输的数据信号。通过对电力线环境建模仿真,实验结果表明,将此优化的算法应用于电力线物联网中可有效去除噪声,去噪后比去噪前信号的信噪比提高了2倍,且相比于直接应用鲁棒性独立分量分析算法,使用松弛因子优化后的算法使得去噪过程中不会出现算法不收敛的情况。
电力线通信;物联网;去噪算法;鲁棒性独立分量分析
电力线通信(Power Line Communication, PLC)基于广泛存在的电力传输线来实现数据传输和控制,被广泛应用于照明控制、自动抄表和电力系统遥控遥测等方面[1]。利用电力线通信构建物联网,可使其变得更加容易实现[2-4],但是利用电力传输线进行通信会受到多种噪声的干扰。
主流的电力传输线去噪方法有扩频通信[5]、多载波正交频分复用[6]、小波去噪[7]等。扩频通信可以使系统的误码率降到很低,但系统要提供较大的带宽;多载波频分复用如果遇到复杂噪声环境仍会不同程度地影响载波信号;小波去噪的过程需要进行小波分解,并选择合适的小波基与阀值,计算较为复杂与耗时。
本文拟使用松弛因子对盲源信号处理中的鲁棒性独立分量分析(Independent Component Analysis, ICA)算法[8-9]进行优化,并将其应用于电力线物联网,从而得出一种降噪方法。
1 电力线噪声分析
1.1 噪声的类型
电力传输线中的噪声有5种[10-11]。
(1) 有色背景噪声
有色背景噪声主要由多个低功率的噪声源叠加组合而成,其功率谱密度随频率的增加而降低,随时间的变化缓慢发生变化。
(2) 窄带噪声
窄带噪声主要是调幅正弦波,由中短波广播信号影响产生,持续时间较长,晚上比白天幅度高,功率谱密度随时间变化较为缓慢。
(3) 和工作频率不同步的周期脉冲噪声
和工作频率不同步的周期脉冲噪声包括显示器、电视机等工作产生的干扰,其重复频率和显示器的扫描频率一致,范围大致为50 ~200 Hz。
(4) 和工作频率同步的周期脉冲噪声
和工作频率同步的周期脉冲噪声主要来自可控硅器件(电源开关),其重复频率和工作频率相同或是其整数倍,覆盖规模较大,脉冲的持续时间为毫秒级,功率谱密度与频率负相关。
(5) 随机脉冲噪声
随机脉冲噪声主要由通信环境中开关动作瞬时产生,每个脉冲都影响较大的频带范围,达到时间是不固定的,时间为毫秒级,某些情况下功率谱密度比背景噪声高50 dB。
1.2 噪声分析与建模
根据噪声模型[12],背景噪声可按图1的传输过程通过滤波来产生,噪声源为白噪声,滤波函数表达式为
其中B(Z)和A(Z)分别代表移动平均和自回归。不妨令B(Z)=1,则使用自回归模型即可对实验测得的背景噪声进行估计,从而确定出模型参数。
图1 背景噪声模型
用多个独立的正弦波的相加来仿真窄带噪声,其函数表达式可表示为[12]
其中φi为[0,2π]上的随机数且与时间独立,fi取实际环境会产生影响的广播电台的频率,Ai(t)由背景噪声得到。
脉冲噪声对通信的影响主要是由脉冲幅度,脉冲宽度和脉冲间隔所决定的,因此可考虑使用单位幅度值和单位脉冲宽度的标准化脉冲n0(t)来模拟实际的脉冲噪声,其数学表达式为[12]
其中Ai为脉冲幅度,tw,i为脉冲宽度,ta,i为脉冲发生的时刻,均可以认为是随机变量。
电力传输线中的噪声可能包含一种或是多种的融合。因为源数据信号与噪声是独立的,不同噪声之间是独立的,所以可将噪声看作是一种源信号,即观测信号是各个源信号的加性混合。根据实验观测和噪声模型的仿真计算,噪声都是非高斯性的,电力线信号是亚高斯信号,信号的零均值性可以在获得观测信号后通过中心化实现,所以电力线信号基本满足ICA的要求,使用ICA算法可以去除电力线物联网中的噪声。
2 ICA及鲁棒性ICA算法
ICA是盲源信号处理中的一种信号分离技术[8],鲁棒性ICA算法是一种新型的算法,以信号的非高斯性作为度量准则,在独立性的前提条件下,对观测信号组进行分离,提取源数据信号。
2.1 独立分量分析
ICA算法的流程如图2所示。S(t)为源数据组成的N维矢量信号,经过信号混叠系统线性组合生成观测信号
X(t)=AS(t),
即实际中接收到的信号。其中A是未知的,然后经过信号分离分解出估计信号
Y(t)=WX(t)。
其中W称为分离矩阵,需要通过ICA算法获得。计算出的Y(t)为源信号矢量S(t)或其某些分量的可靠估计,两个矢量中各个分量的排列次序和幅度可能会不相同。
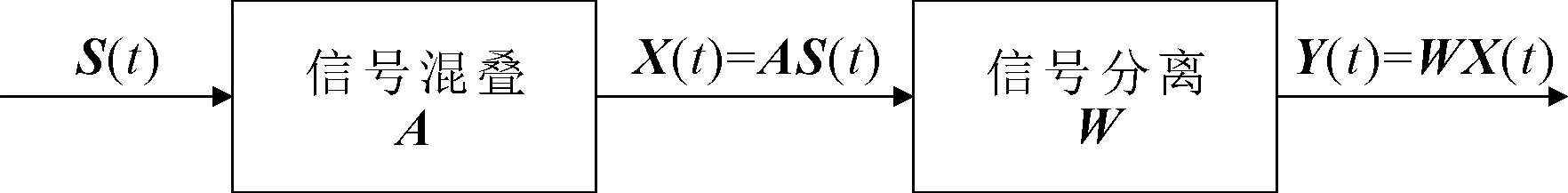
图2 独立分量分析分离过程
ICA算法有以下前提条件。
(1) 源信号组S(t)的各个分量具有统计独立性或尽可能达到独立。
(2) 源信号组均值为0,最多只有一个具有高斯分布。
(3) 混合矩阵A是一个列满秩矩阵,在实际中尽量使得源信号S(t)和观测信号X(t)的个数相同,即A是方阵,逆矩阵A-1存在。
电力传输线中的噪声可以被看作源信号,各个噪声与数据信号共同构成一组源信号,实验仿真时用一个随机矩阵将这组信号混合,基本满足ICA算法的要求,这样就可把源数据信号从混合后的观测信号组中分离出来。
2.2 鲁棒性独立分量分析
鲁棒性ICA算法一种基于峭度和最优步长的ICA算法[9],以峭度作为目标函数进行全局最佳步长搜索,迭代计算满足条件的分离矩阵W,然后还原出源信号的估计值。
观测信号X(t)只用了中心化使其均值为0,并没有进行白化预处理。峭度的公式为[9]
高斯信号的峭度值是0,超高斯信号峭度值大于0,亚高斯信号峭度值小于0,因此峭度是一个适当的目标函数,可以将非高斯信号分离出来。
鲁棒性ICA算法不同于以往的基于峭度的快速ICA算法使用牛顿梯度法,而是利用最优化问题
μopt=arg max|k(W+μg)|,
以目标函数k(W)的梯度
g=Wk(W)
为搜索方向,通过计算对应的多项式的根来获得最优步长,并最终收敛到全局极值点。
鲁棒性ICA的过程可描述如下。
(1) 在每次迭代时,根据接收的数据和当前的W,g值,计算得到最优步长所对应多项式
的系数ai(i=0,1,2,3,4)。
(2) 计算多项式P(μ)的根μi(i=0,1,2,3,4)。
(3) 将根代入峭度表达式的最优化问题,找到满足式最稳定性化问题的μ值。
(4) 更新W+=W+μoptg。
(5) 对W+归一化,即取
(6) 判断条件|1-|WHW+||<ε是否成立,如果成立就找到了分离权值W,如果不成立,则进行下一次迭代。
由以上步骤就可以获得适当的分离矩阵W,将观测信号分离获得估计信号。
3 优化的鲁棒性ICA算法
基于电力线的物联网通信条件恶劣,噪声较多,而且ICA算法计算量较大,对于通信十分不利。以下通过引入预处理过程,并借助松弛因子对鲁棒性ICA算法加以改进。
3.1 预处理
鲁棒性ICA算法无需预白化处理。但事实上,未经预白化处理的观测信号相关性较强,计算时需要多次迭代,用时较长,不利于在电力线这种复杂的环境中使用,所以考虑增加预处理步骤。
预白化处理的一般表达式为
Y′(t)=VX(t),
由主分量分析[13]可知,通过计算观测信号可以得到
其中U和Λ分别代表观测信号的协方差矩阵Cxx的特征向量矩阵和特征值矩阵。
3.2 使用松弛因子优化
实践中当对计算的精度值ε要求较高,而源信号个数较多且相关性较强时,鲁棒性ICA算法的迭代效率较低甚至出现不收敛的极端情况,且在某些情况下预白化处理对鲁棒性ICA算法性能改善有限。使用松弛因子,可以使得算法中的函数获到更稳定的收敛效果,使信号更好分离,从而达到去噪的目的。
引入松弛因子α,将鲁棒性ICA算法的更新过程改进为
W+=W+αμoptg。
选择松弛因子要求在某种范式下满足
‖μoptg‖W+<‖μoptg‖W,
并使得‖k(W+αμoptg)‖达到最小。
松弛因子α可使迭代过程中更新步骤能按给定的范数下降,从而保证算法收敛。结合实验,在迭代的前期(例如前200次)令α=1,即不引入松弛因子,使算法按原来的迭代方式计算;当达到一定的运算次数(大于200次,可能出现不收敛的情况)时,令α=0.5(j-200)(j为计算次数),即加入松弛因子以达到优化算法的目的。
电力线信号中的改进型鲁棒性ICA算法可描述如下。
(1) 将观测信号组预白化处理,降低观测信号X(t)的相关性。
(2) 使用基于松弛因子优化的鲁棒性ICA算法计算分离矩阵W。
(3) 用分离矩阵计算估计值即源信号组。
(4) 从估计值Y(t)中找到需要的数据信号。
4 仿真与分析
通过Matlab软件对改进后的电力线物联网系统鲁棒性ICA去噪算法进行仿真实验。源数据为
00110110011111010001001101100111110100000。
原始数据信号及按噪声模型产生的混合噪声如图3所示。
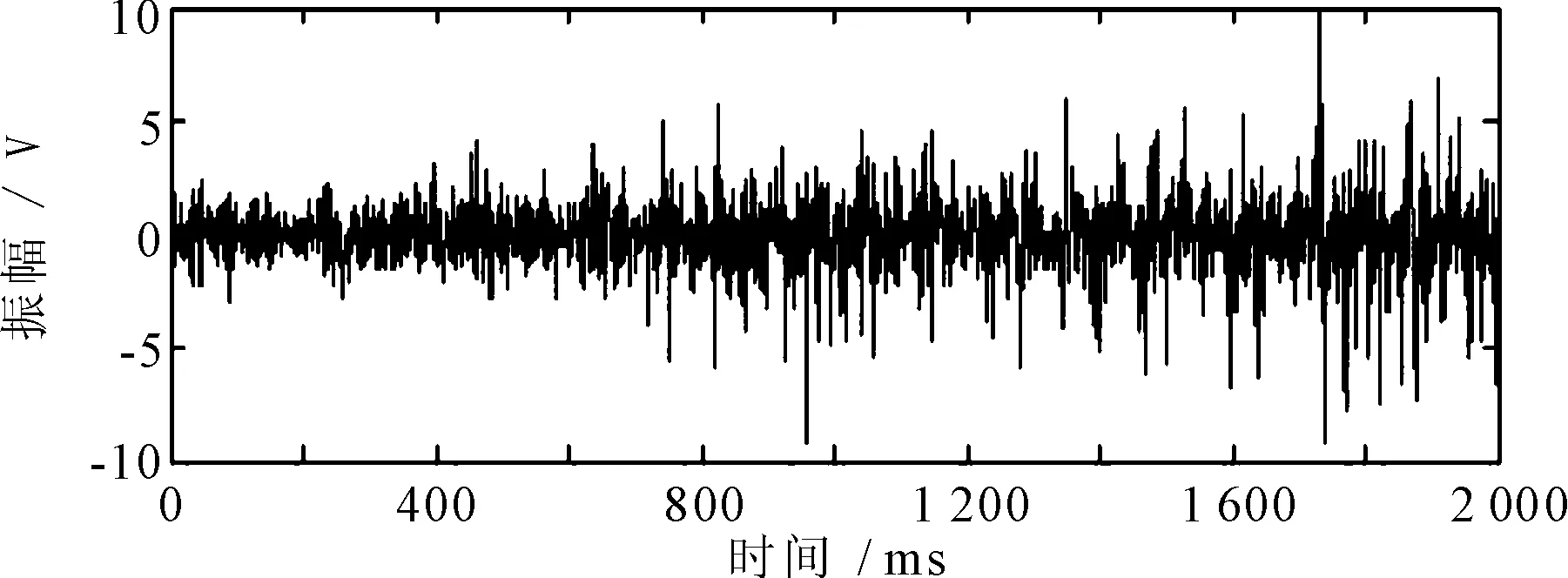
(a) 噪声
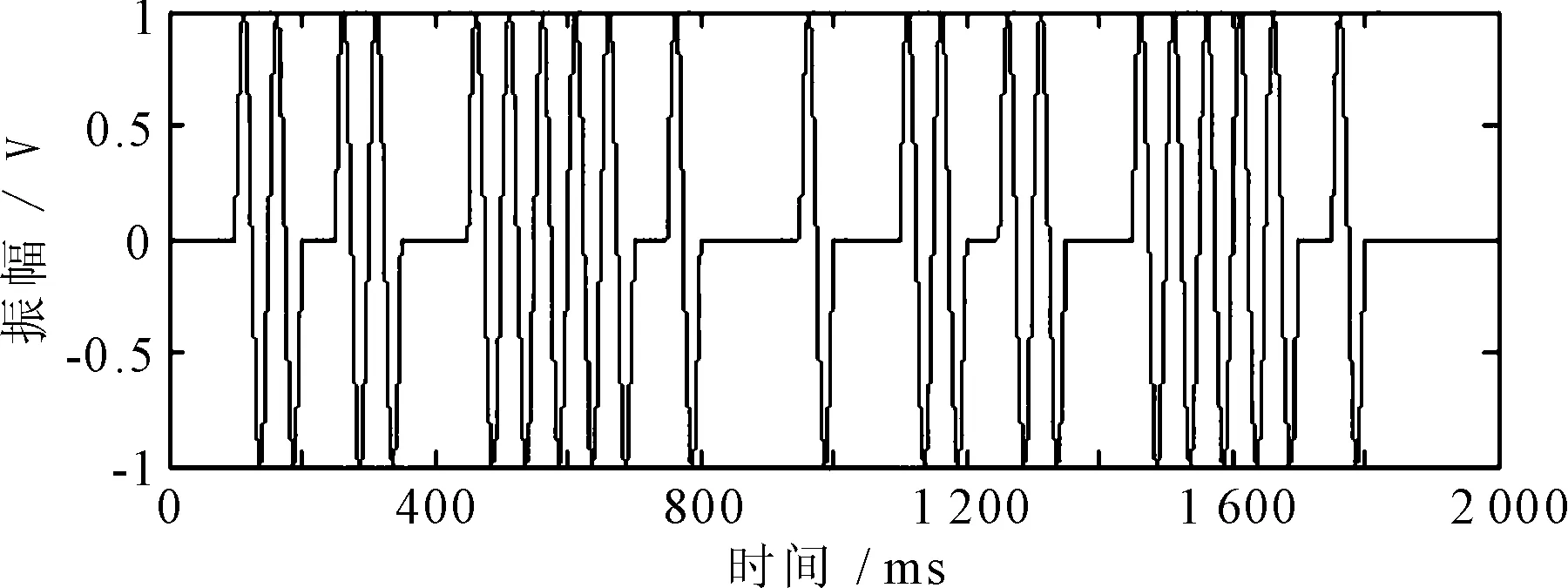
(b) 源数据信号
数据信号与噪声信号混合后如图4所示。
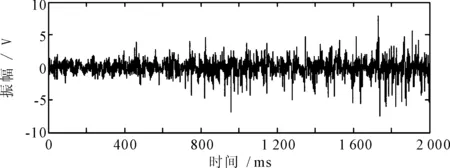
图4 观测信号
从图4基本看不出任何数据。使用鲁棒性ICA算法分离出的估计信号如图5所示。
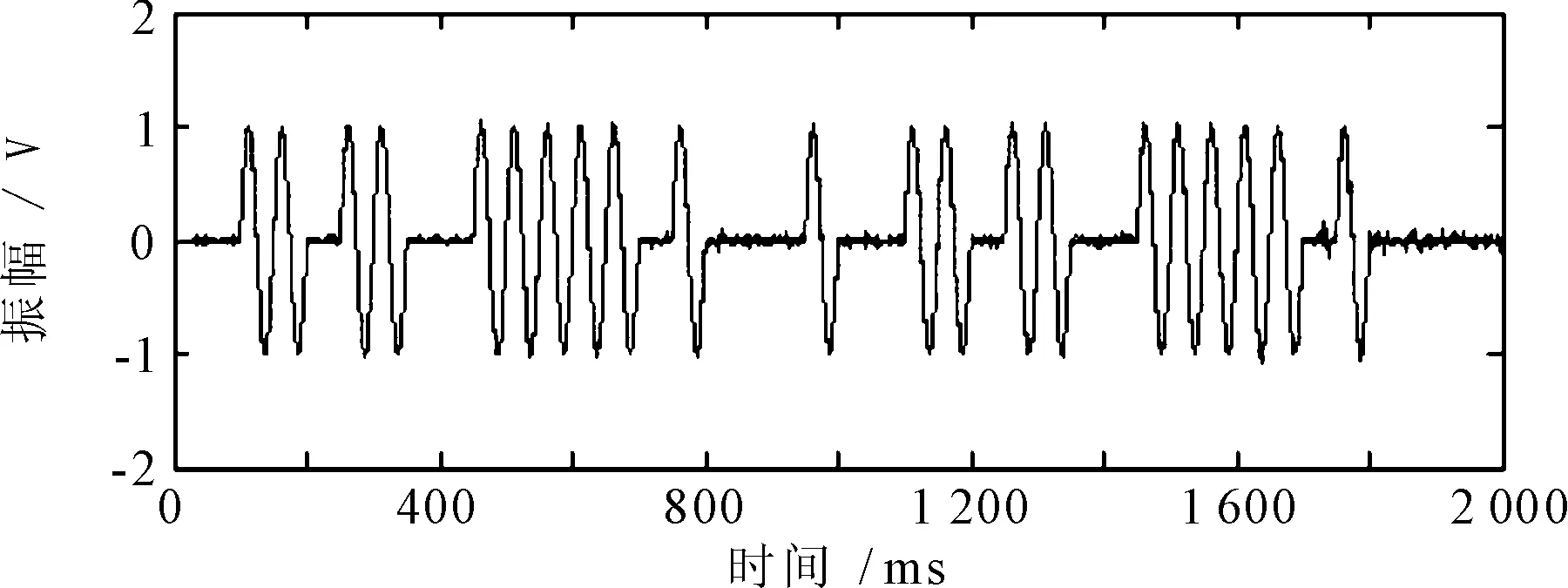
图5 估计信号
比较估计信号和源数据信号,可知去除噪声的目的已经达到。实验平均迭代次数为17,去噪前信噪比约为7.18 dB,去噪后信噪比约为21.12 dB。
将估计信号Y(t)与源数据信号S(t)的互相关系数
作为性能指标,比较不同信噪比下算法的性能,结果如图6所示,从中可见,在信噪比较大时,相关系数达到了0.9以上,估计信号(图5)与源信号(图4)基本一致,算法性能很好;相关系数随着信噪比的降低逐渐减小,即算法性能逐渐下降。
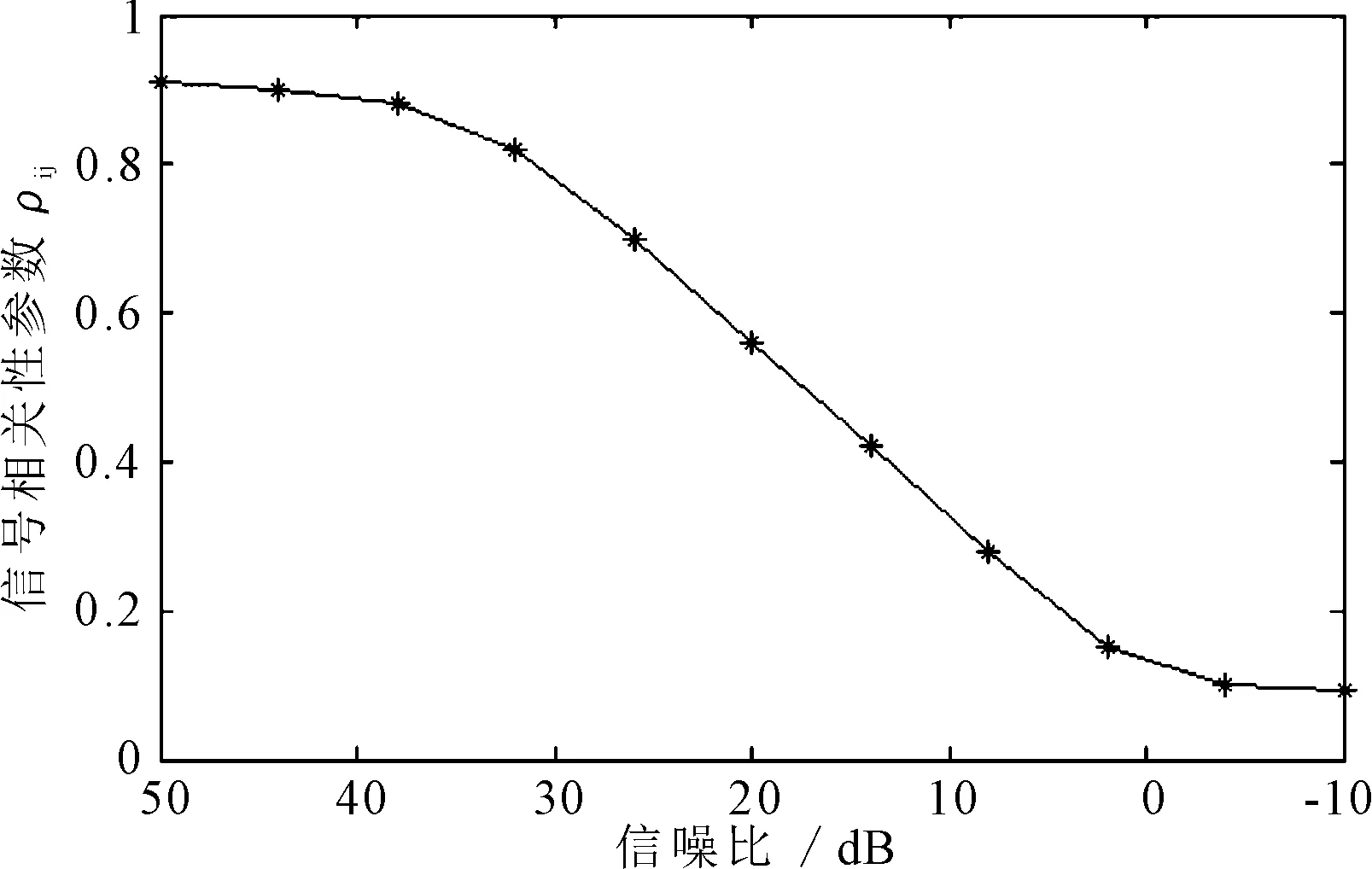
图6 不同噪声时的算法性能
5 结束语
通过引入预白化处理过程,并借助松弛因子对鲁棒性ICA算法加以改进,将其应用于电力线物联网系统以去除信号噪声。实验表明,改进算法可有效去除电力线传输信号所包含的噪声,提高信号信噪比。改进算法具有较高的效率、较好的收敛性和较强的鲁棒性,但对实际估计出的信号,还有排序挑选的问题,有待于进一步研究。
[1] 林维明,华晓辉,王东方.低压电力线通信的现状与展望[J].电力系统通信,2007,28(172):45-48.
[2] 张贝,孙友伟.基于物联网的电力线以太网络适配器的设计[J].西安邮电大学学报,2013,18(2):52-56.
[3] 孙友伟.无线传感器网络与以太网络帧结构转换[J].西安邮电学院学报,2010,15(3):68-71.
[4] 井翠红,孙友伟. 基于电力传输线的新型物联网络TDMA/CSMA协议研究[J].电视技术,2013,37(1):64-66.
[5] 阎啸,刘立业,申妍华,等.电力线扩频通信中复合混沌扩频序列研究[J].电力系统保护与控制,2013,41(3):55-60.
[6] 吴昕,周拥华.高速低压电力线载波通信中的正交频分复用技术[J].继电器,2001,29(10):38-41.
[7] 王振朝,岳莹昭.基于多分辨率分析的小波系数压扩去噪算法[J].中国电机工程学报,2008,28(10):76-81.
[8] 杨福生, 洪波.独立分量分析的原理与应用[M].北京:清华大学出版社, 2006:87-101.
[9]ZarzosoV,ComonP.Robustindependentcomponentanalysisbyiterativemaximizationofthekurtosiscontrastwithalgebraicoptimalstepsize[J].IEEETransactionsonNeuralNetworks,2010,21(2):248-261.
[10]ZimmermannM,DostertK.AnAnalysisoftheBroadbandNoiseScenarioinPowerlineNetworks[C]//Proceedingsofthe4thInternationalSymposiumonPower-lineCommunicationsanditsApplications.Ireland:IEEE,2000:131-138.
[11]HooijenOG.AChannelModelfortheResidentialPowerCircuitUsedasaDigitalCommunicationsMedium[J].IEEETransactionsonEletromagneticCompatibility, 1998,40(4):331-336.
[12] 李平,赵志辉,张振仁.低压电力线信道中脉冲噪声的建模及仿真[J].继电器, 2007,35(5):58-62.
[13] 程瑶.基于独立分量分析的盲信号分离算法研究[D].沈阳:东北大学,2010:25-29.
[责任编辑:瑞金]
Research on noise reduction of internet of things based on power line using independent component analysis
SUN Youwei, SU Shaohua
(School of Communication and Information Engineering, Xi’an University of Posts and Telecommunications, Xi’an 710121, China)
In order to reduce the influence of noise in internet of things, an improved algorithm by using the relaxation factor robust independent component analysis (robust ICA) in blind source signal processing is used in internet of things based on electric power line. The receiver of communication adopts multiplex signals. The correlation of multiple signals is reduced by pre-whitening matrix. Multiple signals are separated by separation matrix estimated by robust independent component analysis algorithm which is based on the relaxation factor. In the end, the data signal is found by the decision threshold. The power line environment modeling and simulation are carried out and the experiment of simulation of power line channel noise shows that the optimization algorithm can effectively remove the noise when applied to power line in the Internet of things. Denoising SNR can be improved 2 times than before. Compared with the direct application of robust independent component analysis algorithm, the relaxation factor optimized algorithm can avoid any un-convergence in the process of denoising algorithm.
power line communication, internet of things, algorithm of denoising, robust ICA
2014-11-17
陕西省教育厅科学研究计划资助项目(12JK0505)
孙友伟(1956-),男,教授,从事下一代通信网研究。E-mail: syw@xupt.edu.cn 苏少华(1990-),男,硕士研究生,研究方向为下一代通信网络与物联网。E-mail: yyysuge@163.com
10.13682/j.issn.2095-6533.2015.06.006
TN913.6
A
2095-6533(2015)06-0023-05

