黄河通信网中码元盲同步的实现
王 磊,丁 燕
(黄河水利职业技术学院,河南 开封 475004)
黄河通信网中码元盲同步的实现
王 磊,丁 燕
(黄河水利职业技术学院,河南 开封 475004)
针对黄河通信网中存在的问题,探讨了在黄河通信网中实现码元盲同步的4个步骤:数据寄存、数据抽取、插值滤波和抽取控制。通过对定时误差和环路滤波优化,该方法能有效提高黄河通信网的通讯性能。
黄河通信网;码元盲同步;全数字解调;数据寄存;数据抽取;插值滤波;抽取控制
0 引言
我国地域辽阔,河流众多,水旱灾害较为频繁且突发性强、地域分布广,尤其是黄河,千百年来,防汛抗旱一直是中华民族社会活动中的重要事件[1]。为了保障人民生命财产的安全,减少水旱灾害的损失,利用计算机及互联网等科技手段进行信息交换、信息处理已成为防汛抗旱指挥中的常态方式。黄河通信网则成为了影响信息传输效率的主要因素。
在现有的黄河通信网中,发送端按照确定的时间顺序逐步传输数码脉冲序列中的每个码元,接收端要正确判决出所发送的码元,就必须有准确的采样判决时刻。因此,接收端必须提供一个确定采样判决时刻的定时脉冲序列,并且这个定时脉冲序列的重复频率必须与发送的数码脉冲序列一致。这样,接收端就能在最佳判决时刻对接收的码元进行采样判决[2]。这种提取定时脉冲序列的过程称为码元同步,它是保证黄河通信网有序、可靠工作的重要支撑。
目前,黄河通信网的接收端会通过数字电路来处理解调过程,即全数字解调。接收端的模拟中频信号经过A/D(Analog/Digital,模拟/数字)采样后,转换成数字信号,被送入数字电路,由数字电路完成整个解调过程。该解调过程具体包括数字下变频、匹配滤波、码元同步、定时同步、载波同步和信道解码等操作。但在现有技术中,码元盲同步对黄河通信网的性能提升非常有限。本文提出了一种新的码元盲同步的实现方法,即在帧同步之前先进行码元同步,可以有效地提高黄河通信网的性能。
1 实现码元盲同步的4个步骤
实现码元盲同步,首先要对黄河通信网接收端接收到的数字信号进行存储,再利用预先设定的抽取控制系数和插值滤波系数对存储的数字信号进行数据抽取,最后利用预先设定的插值滤波系数对存储的数字信号进行插值滤波处理,具体实现过程如图1所示。
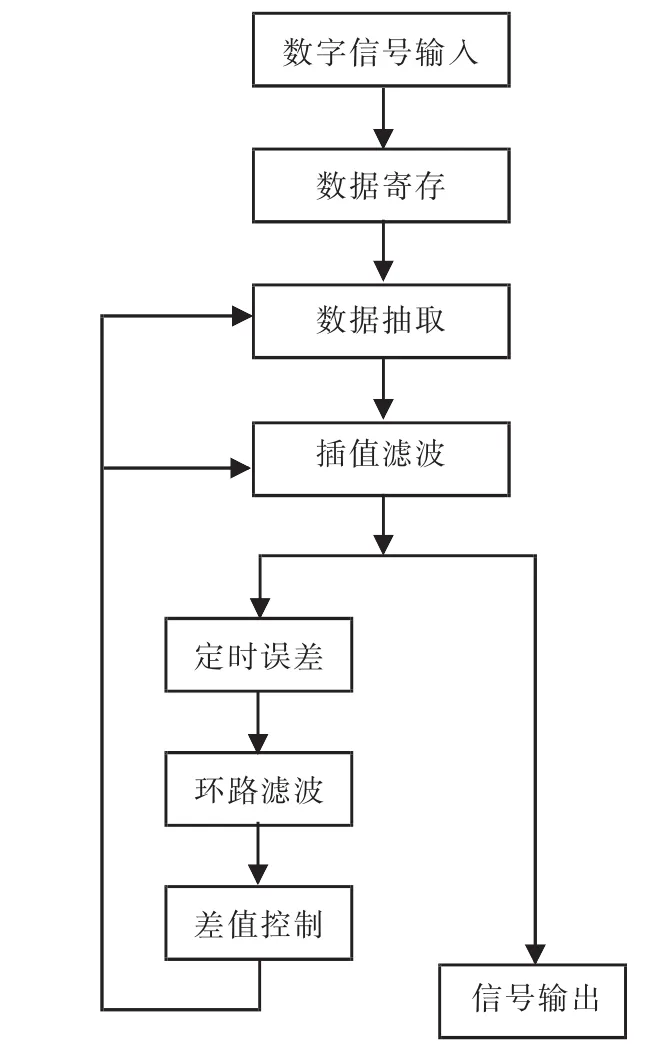
图1 码元盲同步的实现过程Fig.1 Realization process of code element blind synchronization
图1码元盲同步的实现过程中有数据寄存、数据抽取、插值滤波处理、插值滤波和抽取控制系数的计算4个关键步骤。
1.1 数据存储
在黄河通信网的接收端,通过数字电路对经过A/D采样后得到的数字信号进行解调。在此过程中,首先需要通过寄存器对数字信号进行存储。寄存器存储数字信号时,以码元为单位,并且按照码元的先后顺序依次存储。在实际应用中,为了后续的插值滤波处理方便,通常采用4个寄存器来存储上述数字信号,4个寄存器的系数分别设为C0、C1、C2、C3。
1.2 数据抽取
在数据抽取处理过程中,根据插值控制过程计算出的插值滤波系数un+1和抽取控制系数mn+1对寄存器存储的数字信号进行数据抽取,并使抽取的数据实现码元盲同步。
设当前码元的插值滤波系数、抽取控制系数分别为un和mn,下一个码元的插值滤波系数和抽取控制系数分别为un+1和mn+1,判断mn+1+un+1的值比mn+ un的值是否大于等于设定的数值 (该设定的数值可以为2)。如果是,则将接收端收到的信号中的一个码元输入到寄存器中存储,并丢掉寄存器中存储的数字信号中排列在最前列的一个码元。否则,将接收端收到的信号中设定数量的码元输入到寄存器中存储,并将寄存器中存储的数字信号中排列在最前列的设定数量的码元输出。本次设定的数量应与后续的插值滤波处理过程一次处理的数字信号的数量保持一致。例如,插值滤波处理过程一次处理4个数字信号,则上述设定数量为4。
重复执行上述数据抽取过程,可以使得到的输出信号与发送端之间实现码元盲同步。
1.3 插值滤波
对数据抽取过程传输过来的数字信号的各个码元依次采样,并利用插值控制过程传输过来的插值滤波系数对采样后的数字信号进行插值滤波处理。当采用4个寄存器来存储上述数字信号时,插值滤波的计算过程如图2所示。其计算公式为[3]

式中:y(n)为当前码元对应的插值滤波处理后的输出信号;x(mn-1)为上一个码元的采样信号;x(mn)为当前码元的采样信号;x(mn+1)为下一个码元的采样信号;x(mn+2)为再下一个码元的采样信号;C1=0.5u2n-0.5un;C0=0.5u2n-0.5un+1;C-1=0.5u2n+1.5un;C-2=0.5u2n-0.5un;un为当前码元的插值滤波系数,它是根据前面码元的插值滤波处理后的输出信号通过插值控制过程计算得到的。
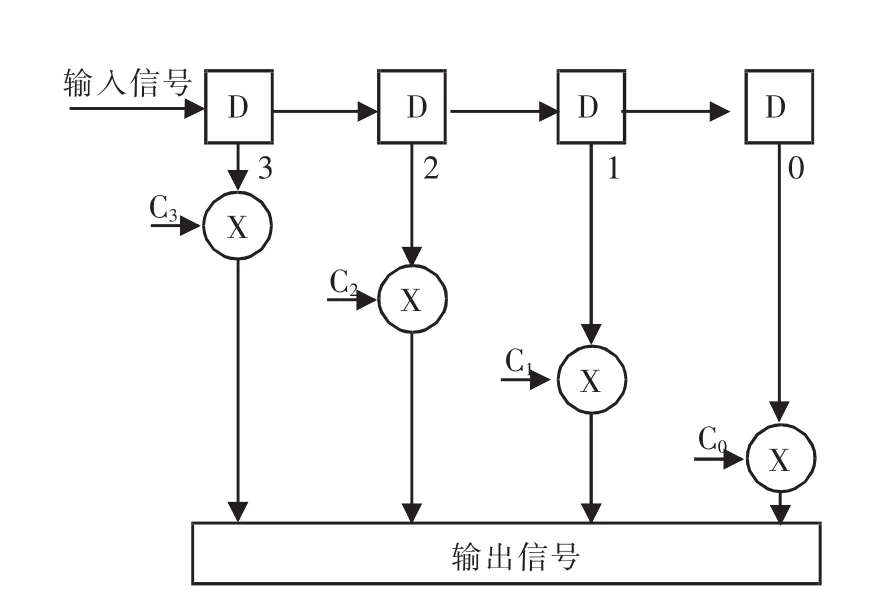
图2 采用4个寄存器插值滤波的计算过程示意图Fig.2 Four registers interpolation smoothing calculation process
设nTi为y(n)对应的采样时间点,即理论上当前码元的最佳采样时间点,则上述nTi的计算过程如图3所示。图3中,mnTs为当前码元的采样时间点,(mn-1)Ts为上一个码元的采样时间点,(mn+1)Ts为下一个码元的采样时间点,(mn+2)Ts为再下一个码元的采样时间点。
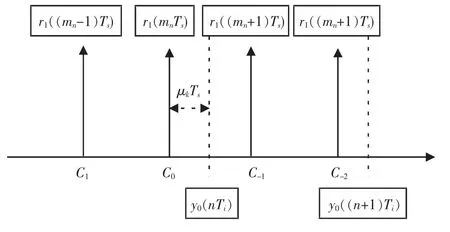
图3 采样时间点nTi的计算过程示意图Fig.3 nTicalculation process of time sample
1.4 插值滤波和抽取控制系数的计算
在插值控制过程中,要对上述插值滤波过程输出的数字信号进行定时误差计算,如图4所示。在定时误差处理过程中,设y(n)、y(n-1)分别为插值滤波处理输出的当前码元、上一个码元所对应的输出信号,y(n-1/2)为所述y(n)与y(n-1)对应采样时间点的中心所对应的输出信号。
定时误差e(n)的计算式为[4]
e(n)=Re{y(n-1/2)[y*(n-)-y*(n-1)]} (2)
式中:Re表示取实部,*表示共轭。
得到定时误差e(n)后,再通过环路滤波器滤去e(n)中的高频分量,得到Δτ(在实际应用中,环路滤波器可以选择有源比例积分滤波器)。然后,通过插值控制过程,根据Δτ计算出插值滤波输出数字信号中的下一个码元(第n+1个码元)的插值滤波系数un+1和抽取控制系数mn+1,其计算公式为:
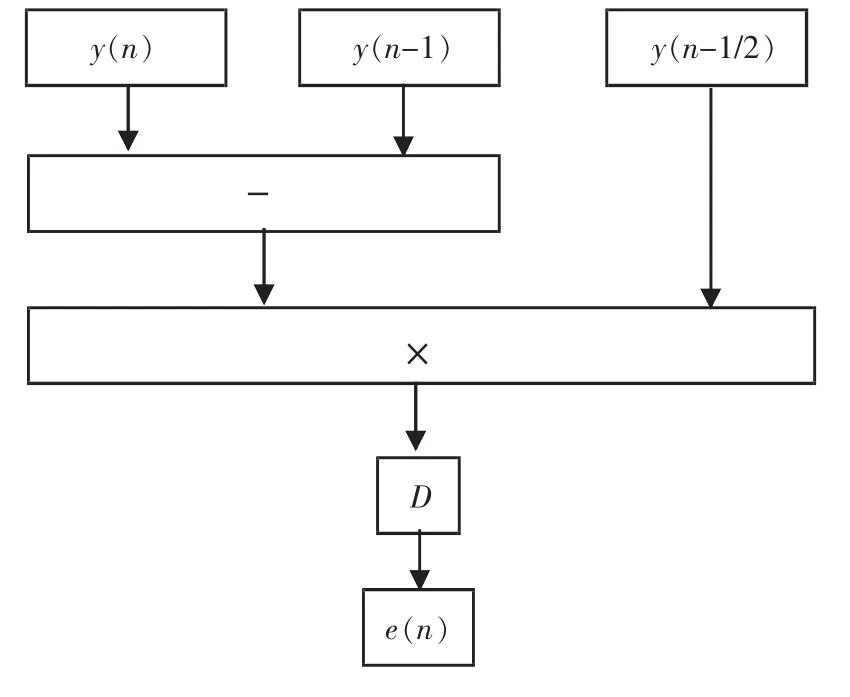
图4 定时误差e(n)计算过程示意图Fig.4 Tim ing error e(n)calculation process
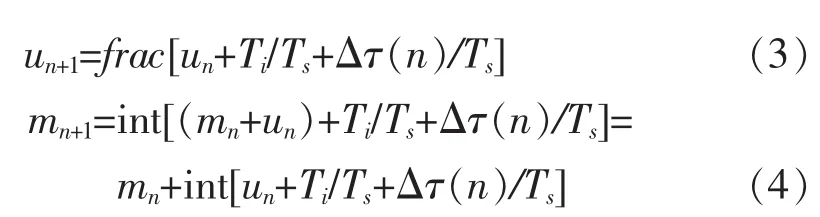
式中:int(.)和frac(.)分别表示取整数和取小数;Ts为黄河通信网发送端的理论采样率(实际采样率因晶振偏差而不同);Ti为黄河通信网接收端的理论采样率 (实际采样率因为晶振偏差而不同);Ti/Ts是一个常数。
在系统设计中,Δτ是e(n)经过环路滤波器处理后的结果。上述插值滤波系数的初始值u1及抽取控制系数的初始值m1都可以设置为0。
在黄河通信网中,码元不同步主要是由发送端采样率Ti和接收端采样率Ts不一致引起的。上述插值控制过程计算得到的Δτ、un+1,可以有效修正发送端采样率Ti和接收端采样率Ts不一致的情况,使接收端和发送端的采样率保持一致,从而达到接收端和发送端码元盲同步的目的。
2 码元盲同步装置构想
根据上述码元盲同步在黄河通信网中实现的过程,设计了一种数字信号处理装置。
该装置主要包含数据存储、数据抽取和插值滤波处理3个模块。
(1)数据存储模块。对黄河通信网接收端接收到的数字信号进行存储。寄存器存储数字信号时,以码元为单元,并且按照接收码元的顺序依次存储。
(2)数据抽取模块。利用抽取控制系数和插值滤波系数对存储的数字信号进行数据抽取。根据插值滤波处理已经输出的数字信号,通过插值控制过程,计算出抽取控制系数和插值滤波系数。
(3)插值滤波模块。利用插值滤波系数对数据抽取后的数字信号进行插值滤波处理并输出,再根据处理后的数字信号,计算出新的抽取控制系数和插值滤波系数。该模块包括插值控制模块和插值计算模块两个子模块。
3 结语
通过对黄河通信网定时误差和环路滤波的优化,实现了码元盲同步,并设计了数字信号处理装置,有效提高了黄河通信网的性能。本文所述码元盲同步的实现方法计算简单、可靠性高、易于实现,可以通过计算机程序指令相关硬件完成,实用性强。
[1]宋曙春.接入网在黄河通信网中的应用[J].黄河水利职业技术学院学报,2003(1):44.
[2]王帆,王新新.基于单片机的数字通信系统位同步提取[J].微型机与应用,2010(23):66-70.
[3]王玉德.数字信号处理 [M].北京:北京大学出版社,2010:110-127.
[4] James D.Broesch.Data Signal Processing[M].USA:Newnes,2010:78-83.
[责任编辑 杨明庆]
TN915.11
B
1008-486X(2015)01-0035-03
2014-10-08
王 磊(1983-),男,河南开封人,讲师,硕士,从事电子信息技术方面的教学与研究工作。

